磁聚焦法测量电子荷质比实验现象分析

尹社会，田 睿

（河南工业职业技术学院 基础部，河南 南阳 473009）

·实验技术·

磁聚焦法测量电子荷质比实验现象分析

尹社会，田 睿

（河南工业职业技术学院 基础部，河南 南阳 473009）

通过利用DS-Ⅲ型电子束实验仪进行电子荷质比测定的实验现象和实验数据的分析，明确了磁聚焦法测量电子荷质比实验中电子束螺旋线起点位置的不确定性，并提出等效起点位置的概念。

磁聚焦法；电子荷质比；等效起点；实验

测量物理学常数是物理学实验的重要任务之一，而且测量的精确度往往会影响物理学的进一步发展和一些重要的新发现。电子质量很小，到目前为止还没有直接测量的方法，但已有不少方法可测得电子的电荷e（如密立根油滴实验）。测量电子荷质比的方法很多，如磁聚焦法、汤姆逊法、滤速器法和磁控管法等。本实验采用的是磁聚焦法测量电子荷质比，实验仪器结构如图1所示。陈秀洪、苏未安通过关于磁聚焦实验讨论了荧光屏上显示的线段与所加电场之间的关系［1］；王勤、黄丽清则探讨了线段与励磁电流之间的关系［2］；王琪等人认为实验的关键点在于励磁电流和螺距的误差［3］；盛飞、江洪建则对实验数据进行了详细的研究，并采用倒推的手段建议修正给定的加速极板距荧光屏距离的标称值［4］。李金波、高海林则分析上述方面后得出电子束螺旋线起点确定为电子束射到屏上之前的最后一个物理交叉点［5］。这一结论基本上已经明确螺旋线起点是一个不确定的点，应引入等效起点的观点。本文则通过实验现象和实验数据分析明确指出等效起点这一概念。

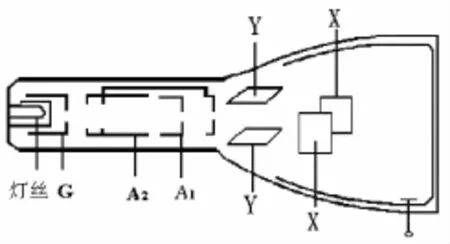
图1 电子束实验仪结构图

1 实验原理

具有速度v的电子进入磁场中要受到磁力的作用，此力为fB=ev×B。设与B平行的分速度为v//；与B垂直的分速度为v⊥；则受磁场作用力的大小取决于v⊥。力的大小为fB=ev⊥B；力的方向既垂直于v⊥，也垂直于B。在力的作用下，电子在垂直于B的面上的运动投影为一圆运动。

另外，电子与B平行的分速度v//则不受磁场的影响。在一周期内粒子应沿磁场B的方向（或其反向）做匀速直线运动。当两个分量同时存在时，粒子的轨迹将成为一条螺旋线，如图2所示。其螺距h（即电子每回转一周时前进的距离）为h=v//T =2π，螺距h与垂直速度v无关。⊥从螺距公式得到=2π只要测得v、//h和B，就可计算出e/m的值。

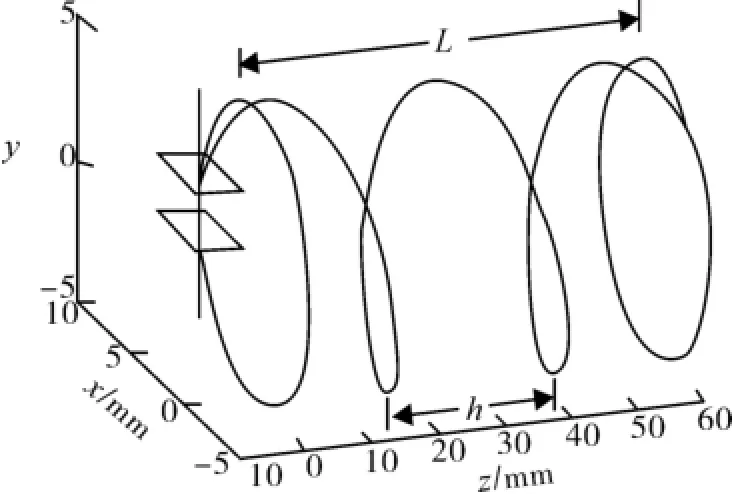
图2 电子螺旋运动示意图

1.1 平行速度v//的确定

采用静电型电子射线示波管，可由电子枪得到水平方向的电子束射线。电子射线的水平速度可由公式=e（UA2-UG），求得：

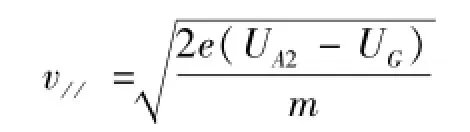
1.2 螺距h的确定

当在X板上加一个偏转电压时，由于两板有电位差，则产生垂直于电子射线方向的电场，此电场将使电子射线得到附加的分速度v//（原有电子枪射出的电子的v//不变）。此分速度将使电子作旁切于中心轴线的螺旋线运动。

当B一定时电子绕行角速度恒定，因而分速度愈大者绕行螺旋线半径愈大，但绕行一个螺距的时间是相同的。如果在偏转板上加交变电压，则在正半周期内先后通过此两极间的电子，将分别得到大小相同的向上的分速度，分别在轴线右侧作旁切于轴的不同半径的螺旋运动，荧光屏上出现的仍是一条直线。

只要保持B不变，不同时刻从“O”点发出的电子做螺旋运动的角速度均相同。不同时刻从“O”点发出的电子，从射出到打在荧光屏上，从螺旋运动的分运动来说，绕过的圆心角均相同，所有亮点都在过轴线的直线上，只是有些亮点早到一段时间。由于余辉时间，在下一个点到来之前，前一个亮点并未消失。这样，在一个交变电压周期时间内，使电子打在荧光屏上的轨迹成为一条亮线，下一个周期重复，仍为一条亮线……各周期形成的亮线重叠成为一条不灭的亮线。

增加B时，在交变电压振幅不变的情况下，螺旋运动的半径减小，所以亮线缩短；同时由于ω增加，在从“O”点发出的电子到达荧光屏这段时间内，绕过的圆周角增大，所以亮线在缩短的同时还旋转。我们总可以改变B的大小，使得在这段时间内，绕过的圆周角刚好为2πrad。这样，电子从“O”发出，作了一周的螺旋运动，又回到轴线上，只是向前了一个螺距h。这时荧光屏上将显示一个亮点，这就是所谓的一次聚焦。一次聚焦时，螺距h在数值上等于示波管内偏转电极到荧光屏的距离L′，这就是螺距h的测量方法。

如果继续增大磁场，可以获得第二次、第三次聚焦等，这时螺距h=L′/2，h=L′/3，…

接通螺线管励磁电流，调节励磁电流使其由零逐渐增大，观察荧光屏亮线的变化（屏上的直线段将边旋转边缩短，直到收缩为一点）。当聚成一点时，记录励磁电流I1。继续增大电流，当第二次聚成一点时，记录励磁电流I2及加速电压UA1，求相当于一次聚焦时励磁电流I=

1.3 磁感应强度B的确定

螺线管内轴线上某点磁感应强度B的计算公

式中：μ0为真空中磁导率；n为螺线管单位长度的匝数；I为励磁电流；β1、β2是从该点到线圈两端的连线与轴的夹角。

若螺线管的长为L，直径为D，则距轴线中点O为x的某点如图3所示。

图3 螺线管示意图

理论计算表明：

式中：B是x的非线性函数。若L足够大，且使用中间一段时，则可近似认为均匀磁场，于是B= μ0n I；若L不是足够大，且实验中仅使用中间一段，则可以引入一个修正系数K，即¯B=Kμ0n I。

2 实验数据处理与分析

在标称值情况下的实验数据处理后结果如表1所示。栅极G距荧光屏距离的标称值为L′= 0.199 m；实测螺线管内长L=0.238 m；螺线管内径D1=0.086 5 m，螺线管外径D2=0.094 5 m；螺线管线径实测值φ=0.000 74 m；单层匝数为322；总匝数N=1 610（以5层计算）；电子荷质比公认值为=1.759×1011C·kg-1。

表1 实验结果数据表 （荷质比单位：×1011C·kg-1）

由表1可计算出荷质比的平均值为1.021× 1011（C·kg-1），相对误差的平均值为41.96。通过理论分析和数据计算可知，实验中励磁电流和螺旋线螺距误差引起的不确定度在总的不确定度中占有的比重最大。由此，可以推断出不同螺旋线第一次聚焦起点的确定可能有误。于是，可由电子荷质比的公认结果倒推螺旋线第一次聚焦的起点，也就是式中L′的值［4-5］，如表2所示。

实验过程中，通过比较阴极到荧光屏的距离L1=0.193 m、栅极到荧光屏的距离L2=0.190 m和第二阳极到荧光屏的距离L3=0.153 m之后，该值较接近于第二阳极的后极距荧光屏距离的实测值。但是我们不能盲目断定螺旋线的起点位置，而是应该理性考虑这一结论，考虑到电子束管内部电磁场分布的复杂性。我们提出等效起点的概念，即螺旋线的起点位置不是一个固定的仪器的某一个具体的参考点，而是由复杂的各种因素共同决定的一个物理点。这样学生在学习时也比较容易接受。当然根据实际情况，我们可以采取文献［5］所得第二阳极的后极的结论。

表2 据实验数据倒推L′的值

由表2可计算出L′的平均值为0.152 m。

3 结束语

为消除地磁场的影响，可将螺线管东西方向放置，或改变励磁电流方向测两次取平均值；为消除某些随机因素的影响，可改变加速电压重复测量几次，取平均值。实验结果显示，根据实验所用电子束线管具体结构的不同，电子束螺旋线的起点具有很大的不确定性，所以提出等效起点的概念是比较合理的方案。

［1］陈秀洪，苏未安.关于磁聚焦实验中荧光屏上显示的线段与所加电场之间的关系［J］.大学物理，2007（7）：45-47.

［2］王勤，黄丽清.关于磁聚焦法测定电子荷质比实验中荧光屏上显示的线段与所加励磁电流的关系［J］.大学物理实验，2004（3）：4-7.

［3］王琪，卢佃清，李新华.电子束实验仪测荷质比及其测量结果的不确定度评定［J］.实验技术与管理，2006，23（2）：26-28.

［4］盛飞，江洪建.电子束聚焦测量电子荷质比的误差分析与研究［J］.天津理工大学学报，2006（3）：66-69.

［5］李金波，高海林.磁聚焦法测定电子荷质比实验电子束螺旋线起点的确定［J］.南阳师范学院学报：自然科学版，2009（9）：37-38.

Analysis of Magnetic Focusing Method to Electron Charge-mass Ratio Experiment

YIN Shehui，TIAN Rui
（Department of Basic Teaching，Henan Polytechnic Institute，Nanyang 473009，China）

The experimental phenomena and the experimental data of electron beam electron chargemass ratiomeasurementwere analyzed.DS-Ⅲtype experimental device has been used to finish thismeasurement by usingmagnetic focusingmethod.The experiment of electron beam spiral cleared starting position uncertainty and the conceptof equivalent starting position has been put forward.

magnetic focusingmethod；electron chargemass ratio；equivalent starting position；experiment

O441.5

A

10.3969/j.issn.1672-4550.2014.02.001

2013-03-26

南阳市科技攻关项目（2012GG035）。

尹社会（1979-），男，硕士，讲师，研究方向：物理课程与教学理论。