钢筋石笼起动流速试验与流场结构数模分析

叶恩立，周宜红,，肖焕雄，任 磊

钢筋石笼起动流速试验与流场结构数模分析

叶恩立1，周宜红1,2，肖焕雄1，任 磊3

(1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 三峡大学水利与环境学院，宜昌 443002；3. 爱尔兰国立大学工程与信息学院，高威)

介绍了钢筋石笼起动流速的研究现状，针对其不足，用石笼实际边长代替化引直径，经过理论推导，提出了以拖拽力系数为主要待定参数的钢筋石笼起动流速简化公式，并在此基础上进行了aac××形石笼的起动流速水槽试验．通过试验，分析了扁度与稳定性的关系，得到了不同扁度所对应的拖拽力系数值并讨论了底部摩擦力系数f给钢筋石笼稳定性所带来的重要影响．此外，为更好地了解钢筋石笼周围流场的特性，构建了一个透水性绕流数值模型，并以大涡模拟为计算手段，对透水性绕流场进行了三维数值模拟．通过将模拟结果与非透水性绕流场从流场结构、涡体脱落、静压强分布以及拖拽力系数等方面进行定性、定量的对比分析，得到了透水性对流场的具体影响结果．

钢筋石笼；起动流速；水槽试验；方钝体透水性绕流；大涡模拟

如何减轻截流难度，一直是水利水电工程设计、施工中颇受关注的问题．从增大抛投料自身稳定性从而减轻截流难度的角度出发，钢筋石笼尤其是钢筋石笼串在立堵截流工程中得到了越来越多的应用．

钢筋石笼是将工程开挖料或现场易于获得的天然中小石料装入已编制好的钢筋笼而制成的，具有相对较强的透水性和柔性．葛洲坝、三峡以及溪洛渡等工程的截流实践表明，其稳定性优于同吨位的混凝土块体且不逊于同吨位的特大石．同时，其材料的获取和制作的过程却要比特大石和混凝土块体方便得多，因此，受到越来越多的关注和应用．但到目前为止，国内外有关钢筋石笼稳定性的研究成果很少，使得钢筋石笼(串)在工程应用中缺少相应的理论指导，给截流设计工作带来了困难．因此，对钢筋石笼稳定性机理的研究具有实际意义和学术价值．针对钢筋石笼起动流速现行研究中的不足，本文从石笼的特性出发，用实际边长代替化引直径，对单个钢筋石笼的起动流速进行了理论推导，提出了以拖拽力系数为主要待定参数的钢筋石笼起动流速公式．结合aac××形石笼的起动流速水槽试验，分析了扁度与稳定性的关系，得到了不同扁度所对应的拖拽力系数值，并指出了底部摩擦力系数f对钢筋石笼稳定性的影响．此外，由于传统试验手段很难对钢筋石笼周围流场结构进行无干扰精确观测，所以为了更好地了解钢筋石笼周围流场的特性，构建了一个透水性绕流数值模型，并以大涡模拟为计算手段，对透水性绕流场进行了三维数值模拟．通过将模拟结果与非透水性绕流场从流场结构、涡体脱落、静压强分布以及拖拽力系数等方面进行定性、定量的对比分析，得到了透水性对流场的具体影响结果，为研究钢筋石笼稳定性机理提供了参考．

1 研究现状

目前，关于截流抛投材料的起动流速研究有很多成果，也出现了许多起动流速公式，其中大多数均脱胎于经典的伊兹巴斯公式[1]，即

式中v、K、D、sr、r分别为作用在截流材料上的来流平均速度、稳定系数、抛投块体化引直径、抛投块体容重以及水的容重．

伊兹巴斯公式及其类似公式(以下简称伊类公式)中的未知自变量少，应用起来相对简单，但其将影响材料稳定性的接触面粗糙程度、拖拽力系数、上举力系数、流速分布等因素全部用稳定系数K来体现和替代，不免显得过于笼统，K值的物理意义也不够明确，最终导致其值波动较大．汪定扬[2]根据试验和收集到的资料，发现K值的变化范围是0.4～2.7，这样就给在实际应用伊类公式时K值的准确选取带来了困难．为此汪定扬通过多年的试验研究，利用日本学者岩恒雄一的摩擦系数公式[3]对K值进行了分解，得到了块体稳定实用计算公式，其基本关系为

式中：A、B、n为待定参数，根据平堵、立堵等形式的不同由试验确定；H为截流龙口水深；/HD为相对水深；/DΔ为相对糙度；α为断面流速分布系数，根据不同情况由试验确定．

以上所述是针对一般截流块体所提出来的，而有关钢筋石笼稳定性的研究成果却很少．2010年，李学海[3]对钢筋石笼的稳定性进行了一系列卓有成效的试验研究，引入了泥沙研究中所常用的扁度系数λ[4]，并结合块体稳定实用计算公式，提出了钢筋石笼抗冲稳定计算公式，其基本关系为

式中：a、b、c分别为钢筋石笼长、中、短轴的长度；A、B的值分起动和止动两种情况，通过试验拟合得到．

在文献[3]中，经过验证，式(3)具有相当的精度．但以上研究仍然存在以下两方面不足．

(1) 用化引直径D来简化与球体形状偏离较大的方块体，则化引过程(一般是等体积化引)缺乏清晰的物理和数学根据；并且，块体的摆放方式也不能得到体现，例如，长轴横水向摆放与顺水向摆放时的起动流速显然不同，而采用化引直径则认为与摆放方式无关了(因为此时不存在长、短轴了)．虽然式(3)有扁度系数的矫正，而且在应用时也能够得到工程允许的结果，但从学术研究的角度，用3个几何尺度来定义钢筋石笼的形状，则能更清楚地研究影响其稳定性的因素，有助于理解其稳定性机理．

(2) 式(2)和式(3)都没能很好地处理块体底部摩擦力的问题．例如，假定块体与底部接触面十分光滑(接近于没有摩擦力并忽略分子间的作用力)，那么根据经典力学，块体即使受到很小的力(接近于零)的作用也会发生起动，即起动流速接近于零．这一点从式(2)和式(3)中并不能得到体现，说明此类公式并没能全面地反映出起动流速关系．

本文正是针对以上不足作为研究出发点．

2 问题分析

钢筋石笼在水流的作用下主要受5个力的作用：拖拽力DF、上举力LF、重力G、浮力fF和阻力zF，其受力分析如图1所示．从图中可以看出，钢筋石笼与其他截流材料相比，在受力个数及性质方面都一样．导致钢筋石笼与其他截流材料稳定性的不同主要是与其他截流材料相比，钢筋石笼有3方面的差异：一是透水性不同；二是与水体接触产生的表面摩擦力不同；三是与河床接触产生的底部摩擦力不同．研究钢筋石笼的起动流速需将重点放在这3点不同上，其中，前两方面的不同是通过拖拽力和上举力体现出来的．

图1 钢筋石笼受力分析示意Fig.1 Schematic diagram of force analysis of rock-filled steel cage

浸没在水中的物体在与水流发生相对运动的情况下，由于水的黏性，在其运动方向上会产生拖拽力FD．拖拽力FD由压差阻力Fpress和摩擦阻力Ffric组成，两者的比例关系取决于物体的形状[5]．但在计算拖拽力时，并没有将两者分开来，其计算式为

式中：DC为拖拽力系数；tA为特征面面积．

特征面的选取需根据块体的形状而定，分为下列3种情况．

(1) 迎水面．适合迎水面相对较大、短粗类钝体，例如球体、圆柱体、导弹、鱼雷等形体．

(2) 俯视面．即为来流方向上的投影面，适合扁平形体，例如机翼、平板等．

(3) 湿面．主要适用于船只等浮体．

此处，研究钢筋石笼时，应该选择第1种，即选择迎水面为特征面来计算拖拽力．

钢筋石笼在流水中，由于顶部和底部的流速不相等，根据伯努利方程，会产生压力差，表现为上举力FL，其计算公式为

式中：CL为上举力系数；A1为钢筋石笼在来流方向的投影面积．

上述CD和CL并不是常数，而是根据块体形状、雷诺数、攻角等的不同而发生变化．对于它们之间变化的规律，有很多经验性的公式和成果，但还远远不够，不能给出成熟的计算公式．对于不同的问题，往往还是通过试验，根据式(4)和式(5)反求CD和CL．针对本文要研究的六面体类的块体，CD只和块体形状有关，CL只和来流雷诺数有关[6]．

以滑动为条件，列出钢筋石笼起动时的力学平衡方程，即FD=Fz，可得

式中f为底部摩擦力系数．

如上所述，钢筋石笼与相同形状的六面体混凝土块体相比有3方面的差别，前两方面的差别在式(6)中是通过DC和LC体现出来的．所以当底部情况一定时，研究钢筋石笼起动流速的关键在于确定式(6)中的DC和LC．当然，不同的钢筋石笼还涉及到密实度的问题，这在式(6)中可以通过sr来体现．

3 模型试验及分析

钢筋石笼起动流速试验是在1∶50的水槽中进行的．水槽长22,m，宽32,cm，深30,cm，槽身、槽底均采用有机玻璃制造．本试验以1∶50的比尺、按不同的质量、分不同形状制作了试验所需的钢筋石笼，具体规格见表1．其中，由于工程中用立方体和长条形(包括扁形)的钢筋石笼居多，所以与韩其为[4]在泥沙研究中所定义的扁度系数不同，这里重新定义了扁度系数，即(a、b、c所示尺寸见图1)．另外，为了排除迎水面摆放形式(即将a边垂直于底板放置还是平行于底板放置)给问题分析所带来的影响，本次试验只制作了aac××形(即ab=)的钢筋石笼，后文得到的DC与gλ的关系也仅限于aac××形的钢筋石笼．

起动试验程序：预先将试验钢筋石笼放置在试验段底板上，为减小位置随机性所带来的影响，每次将石笼放置在同一位置上；然后调节上游闸门的开度，直至石笼开始滑动(滑动速度较慢)为止，取出石笼，用小旋桨流速仪测量钢筋石笼迎水面中心点处的流速，每次起动后记录15次流速，分析时取算数平均．为降低脉动随机性带来的影响，以2,min为调节上游开度的时间间隔．需要说明的是，由于本文研究的流速不是沿垂线的平均流速，并且不用像研究泥沙细颗粒时需要考虑薄膜水附加下压力[7-8]，所以在这里不用考虑每次试验的水深．

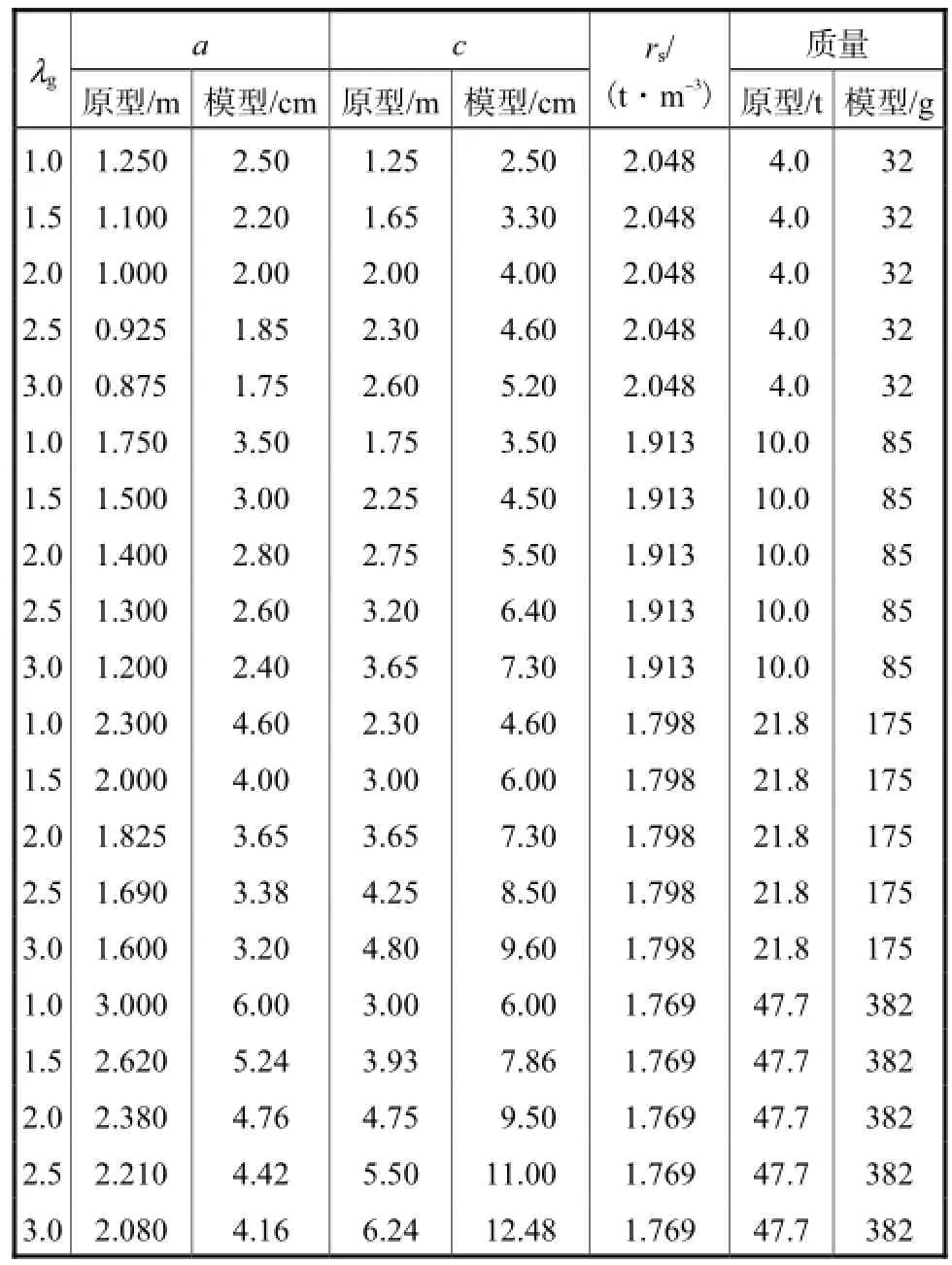
表1 试验钢筋石笼规格Tab.1 Size of rock-filled steel cages for test

经过多组反复试验，经过算数平均整理过的试验结果见表2和图2．

表2 流速试验结果Tab.2 Results of velocity tests

从图2中可以发现，λg的值从1.0到2.5变化时，钢筋石笼的起动流速有逐渐增大的趋势，并且在λg=2.5时起动流速达到最大．究其原因，从拖拽力来看，随着λg值的增大，迎水面的面积在减小，假定拖拽力系数不变，则拖拽力越小，起动流速就越大．但在λg=3.0时有所减小，则很可能是由于底部面积增大，上举力的影响超过了拖拽力，导致了起动流速的减小．

图2 不同λg对应的质量和速度关系Fig.2 Relationship between mass and velocity under different λg

由于本次试验条件的限制，缺乏单独针对CD和CL而进行的试验，并且考虑到石笼的透水性，在底部面积不大时，上举力的影响远小于拖拽力对稳定性的影响，所以为了分析方便，将上举力和拖拽力的影响都通过拖拽力系数来体现，为此，式(6)简化为

式(7)就是钢筋石笼起动流速简化计算公式．式(7)从参数来看，仿佛与石笼的迎水面边长a、b没关系，其实，当c一定时，a、b对石笼稳定性的影响可以通过DC来体现，因为正如上文所述，DC是形状的函数．

需要说明的是，对于钢筋石笼来讲，其sr(体现了透水性强弱)也会对DC产生影响，但考虑到本次试验钢筋石笼(实际工程中也一样)的sr变化不大，对DC产生的影响有限，所以本文在分析DC时，就忽略了sr的变化对DC产生的影响．

根据试验所得流速数据以及实际测得的f值(0.21f=)，代入式(7)，就可以得到aac××形钢筋石笼不同gλ值所对应的拖拽力系数DC(见表3)．

表3 不同gλ对应的DC值Tab.3 Values ofDC under differentgλ

为了验证式(7)在钢筋石笼为aac××形时的准确性，现以李学海[3]在光滑水泥面上所进行的立面体钢筋石笼起动流速试验数据为基础，对g1.0λ=情况下(缺少其他情况资料)这两次试验的数据和由公式计算出的数值进行了对比，结果见图3，其中，根据对钢筋石笼与光滑水泥面的摩擦系数所进行的试验，摩擦系数取为0.48．

图3 gλ=1.0时不同f值对应的质量和速度试验及计算数据Fig.3 Relationship between mass weight and velocity accord-ing to computation and test under different f whengλ=1.0

由图3可知，本文公式具有一定的精度和适用性．另外可以看出，摩擦系数f对钢筋石笼的稳定性有很大的影响．例如当0.21f=时，47.7,t的钢筋石笼的起动流速为3.65,m/s，而当0.48f=时，2,t的钢筋石笼就已经可以抵抗4,m/s的流速了．需要说明的是，底部摩擦系数对稳定性的这种影响不是钢筋石笼所特有的，对所有块体的稳定性研究都需十分重视摩擦系数的影响．现阶段由于缺乏对摩擦系数实质性的研究(事实上，关于摩擦力的本质目前尚未有定论)，所以在实际应用中还不能够由函数关系来对摩擦系数做出确定，往往还需要用试验来确定，有时甚至不直接考虑摩擦系数的影响．因此，怎样实现和评估试验环境中的摩擦系数与实际工程中的摩擦系数之间的转换值得深入研究，否则，由于摩擦系数的重要影响，当把室内试验所获得的结论向实际情况转化的过程中就会存在较大的差别，从而使室内试验失去了其指导实际工程的作用．

4 数值模拟及分析

用传统试验手段很难对精细流场结构进行清晰的观察，并且任何接触性测量都不能对反映流场性质的物理量进行无干扰地测量，所以本文以发展较快的CFD技术为研究手段，建立了一个透水性方钝体绕流模型，以更好地观察钢筋石笼周围流场的特性，继而从另一个角度来帮助理解透水性对钢筋石笼稳定性的影响．

4.1 模型建立

4.1.1 湍流模型选取

钝体绕流，特别是像方钝体这样带有锐缘(sharp edge)的绕流，周围流场结构相当复杂，其中涉及到碰撞、分离、回流以及非定常涡体脱落等复杂的湍流现象，具有高度的三维特性．目前，在计算流体力学领域，一般有3种方法用于模拟湍流：直接数值模拟(DNS)、雷诺平均法(RANS)和大涡模拟(LES)．

DNS在计算复杂的湍流时，必须采用很小的时间和空间步长，网格划分需要达到科尔莫戈洛夫微尺度(Kolmogorov microscale)的精度．据计算[9]，当雷诺数达到1×106时，应用DNS计算三维问题需要的网格节点数约为1×1013，所以，用DNS模拟湍流计算代价过高，很难实现．

RANS模型中，主要包括标准k-ε模型、修正k-ε模型以及雷诺应力(RSM)模型．

20世纪80年代，Mochida等[10]首次发现了标准k-ε模型在模拟像方钝体绕流这样带有碰撞现象的三维流动时，在碰撞区域会产生湍动能k过大的失真现象，如图4[10]所示．之后，Rodi[11]通过与试验[12]对比，发现标准k-ε模型对方钝体顶部流动的模拟与试验结果有较大的出入；之后，经过修正的k-ε模型，例如Kato等[13-14]提出的LK k-ε模型，由于较好地克服了湍动能过大现象，其模拟结果相对于标准k-ε模型来讲，与试验结果符合得较好．然而，对于方钝体后部回流区的模拟，所有RANS模型的模拟结果都存在回流区长度过长而失真的现象，而大涡模拟则能够更好地处理以上问题[12]．所以本文以大涡模拟方法为研究手段(并不对大涡模拟数值方法本身进行讨论)对问题展开研究．

图4 标准k-ε 模型模拟时产生的湍动能过大现象(取中垂面)Fig.4 Over-production of turbulent energy by the standard k-ε model(center section of cube)

4.1.2 计算条件

本文来流雷诺数Re=2.2×104(依据方钝体边长和进口平均流速得到)，参考前人[13-16]计算经验，规定本文模拟的计算条件，见表4．

文中采用标准Smagorinsky亚格子格式，Cs取0.12．用二阶中心差分离散空间导数，用Adams-Bashforth格式离散对流项，Crank-Nicolson格式离散扩散项．采用变时间步长，当迭代收敛性较好且趋于稳定时，采用的时间步长Δt=0.0002s ．文中进行了5×105个时间步的计算，以达到稳定的周期条件，随后又进一步进行了5×105个时间步的计算，以便在做数理统计处理时能得到较为可靠的平均值．为了使方钝体具有透水性，在方钝体迎水面、背水面、侧面及顶面开口，具体尺寸见图5，计算域网格如图6所示．

表4 计算条件Tab.4 Computational conditions

图5 计算模型示意Fig.5 A schematic diagram of computational model

图6 计算域网格划分Fig.6 Meshes of computational domain

4.2 计算结果及分析

4.2.1 流场结构观察

图7显示了在6.5xH=的截面上，透水性和非透水性绕流在不同时刻的速度场云图．从图中可以看出，无论是透水性还是非透水性绕流，在方钝体后都会产生涡体脱落现象．但由于透水性的影响，与非透水性绕流相比，在此截面上透水性绕流场主要有4个方面的不同：①方钝体后部涡体产生能力强，涡体形态更加丰富，流态更加复杂；②透水体顶部没有产生明显的回流；③绕流场最大流速较非透水性绕流下降了约12.5%；④涡体脱落过程没有明显的周期性．

图7 =6.5xH截面各时刻非透水性和透水性绕流速度场云图Fig.7 Contours of velocity on the =6.5xH plane of flow passing a non-pervious body and a pervious body at different times

以上特性是基于对x=6.5H截面上各时刻的速度场云图进行观察而得出的，但绕流场具有高度的三维特性，进一步分析则需要更多不同的观察角度．

图8显示了在t=60.5s 以及t=61.0s时刻各截面的速度场云图．从图中可以发现，以x=6.5H截面为界，方体两侧流场结构各自相似．涡体的产生能力，在t=60.5s时刻，从x=7.0H截面至x=6.0H截面呈递增趋势，而在t=61.0s 时刻呈递减趋势．在其他时刻，这种递增、递减现象交替出现，呈现出一定的周期性．此种现象，很可能是由于当流体经过透水体两侧时产生的涡体不对称脱落所造成的(类似于卡门涡街)．

4.2.2 静压强分布

从方钝体周围的静压强方面，透水性绕流和非透水性绕流也有着显著的差别，如图9所示．从图中可以发现：在迎水面的透水部位，静压强较非透水体相同部位要小得多；在顶部，透水体静压强分布比较平稳，几乎没有波动，且其绝对值也要小于非透水体相应部位的静压强值；另外，透水体下游侧所受静压强，除了从BC过渡到CD时，在C点至透水部位有一个较大的波动外，其余部位压强分布较为平稳，同时，从图7和图9可以发现，C点附近也正是透水体背水面产生涡体脱落以及流体分离的主要部位．

图8 纵向各截面速度场云图Fig.8 Contours of velocity in several sections

通过以上对方钝体边壁上静压强分布的分析，可以推断出透水体受力，无论是压差阻力还是上举力，都较非透水体要小．这也从一定程度上解释了在水流作用下，透水性块体的稳定性优于相同形状相同质量的非透水性块体．

图9 沿6.5xH=截面轮廓线平均静压强分布曲线Fig.9 Distribution of time-averaged value of static pressure along the outline of 6.5xH= plane

4.2.3 拖拽力系数计算

拖拽力系数DC定义为

式中：0τ和p分别为方钝体表面微元面积dA上的切应力和压应力；θ为表面微元上的法线与流速方向的夹角．根据式(8)结合数值模拟可提取的结果，可以算出在本文计算条件下，透水体的拖拽力系数约为0.63，非透水体的拖拽力系数约为1.02．其中，透水情况下的拖拽力系数与试验部分相同情况下所测得的拖拽力系数值0.68(见表3)符合得较好．

5 结 论

本文用石笼实际边长代替化引直径，提出了钢筋石笼起动流速简化公式(式(7))．式中以拖拽力系数为主要待定参数，相对于稳定系数K，选取更加方便且有依据(根据扁度系数选取)．通过将公式应用于不同工况，验证了公式的准确性和适用性．通过对aac××形石笼进行水槽试验，以及对透水性绕流场的三维数值模拟，本文还得出了以下结论：

(1) aac××形石笼稳定性随gλ值的增加先提高后减小，并在λg=2.5时达到最稳状态；

(2) 透水体顶部没有明显回流，流场最大流速较非透水性绕流流场下降了约12.5%；涡体主要在下游回流区尾部产生且脱落过程随机性较强，没有明显的周期性，而两侧的涡体交替产生，呈现出一定的周期性；

(3) 通过压强分析，发现透水体所受压差阻力和上举力都要远小于非透水体；

(4) 由数值模拟计算出透水体的拖拽力系数为0.63，与试验结果相差不大．

限于试验条件，本文没有将上举力系数分离出来进行研究，并且部分结论也只适用于单个石笼的特定形状，更复杂的情况可做进一步研究．另外，摩擦系数对截流块体稳定性的研究影响显著，值得引起注意.

［1］ 肖焕雄. 施工水力学[M]. 北京：水利电力出版社，1992.

Xiao Huanxiong. Hydraulics in Construction[M]. Beijing：China Waterpower Press，1992(in Chinese).

［2］ 汪定扬. 立堵截流实用水力学计算[J]. 水利学报，1983(9)：11-19.

Wang Dingyang. Practical hydraulic calculation in enddump river closure[J]. Journal of HydraulicEngineering，1983(9)：11-19(in Chinese).

［3］ 李学海. 深厚覆盖层河床截流若干关键技术问题研究[D]. 武汉：武汉大学水资源与水电工程科学国家重点实验室，2010.

Li Xuehai. Several Key Technology Study for Deep-Thick Covering Layer Riverbed Closure[D]. Wuhan：State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，2010(in Chinese).

［4］ 韩其为. 川江卵石形态与堆积特征调查[G]//全国重点水库泥沙观测研究协作组．推移质泥沙测验技术文件汇编．1980.

Han Qiwei. Research on the shape and the characteristic of gravel in China[G]//Cooperation Group of Research on the Sediment in Important Reservoir of China. Technical Test Documentation of Bedload Sediment．1980(in Chinese).

［5］ White F M. Fluid Mechanics[M]. New York：McGraw-Hill Book Companies，1994.

［6］ Evett J B. Fundamentals of Fluid Mechanics[M]. New York：McGraw-Hill Book Companies，1987.

［7］ 窦国仁. 论泥沙起动流速[J]. 水利学报，1960(4)：44-60.

Dou Guoren. Studies on the critical velocity of sediment[J]. Journal of Hydraulic Engineering，1960(4)：44-60(in Chinese).

［8］ 张瑞瑾，谢鉴衡，陈文彪. 河流动力学[M]. 武汉：武汉大学出版社，2007.

Zhang Ruijin，Xie Jianheng，Chen Wenbiao. River Dynamics[M]. Wuhan：Wuhan University Press，2007(in Chinese).

［9］ Murakami S. Overview of turbulence models applied in CWE-1997[C]//2nd European & African Conference on Wind Engineering. Genova，Italy，1997：22-26.

［10］ Mochida A，Murakami S，Hibi K. Comparison of wind tunnel experiment with numerical simulation by means of k-ε model and LES concerning turbulent flow field and gas diffusion around cubic model[C]// Proc of Architectural Institute of Japan Annual Meeting. Japan，1986：283-284.

［11］ Rodi W. Comparison of LES and RANS calculations of the flow around bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics，1997(69/70/ 71)：55-75.

［12］ Martinuzzi R，Tropea C. The flow around a surfacemounted prismatic obstacle placed in a fully developed channel flow[J]. J Fluids Eng，1993，115：85-92.

［13］ Kato M，Launder B E. The modeling of turbulent flow around stationary and vibrating square cylinders [C]//9th Symp Turbulent Shear Flows. Kyoto，Japan，1993.

［14］ Edwards J R，Boles J A，Baurle R A. Large-eddy/ Reynolds averaged Navier-Stokes simulation of a supersonic reacting wall jet[J]. Combustion and Flame，2012，159：1127-1138.

［15］ Qi Xiaoni，Liu Yongqi，Du Guangsheng. Experimental and numerical studies of aerodynamic performance of trucks [J]. Journal of Hydrodynamics，2011，23(6)：752-758.

［16］ 王小华，朱文芳，何钟怡. 方形钝体受限绕流的三维数值模拟[J]. 计算力学学报，2008，25(5)：671-675.

Wang Xiaohua，Zhu Wenfang，He Zhongyi. Three dimensional large eddy simulation of the flow field and energy loss characterization of a ribbed duct turbulent flow [J]. Chinese Journal of Computational Mechanics，2008，25(5)：671-675(in Chinese).

（责任编辑：金顺爱）

Critical Velocity Test and Flow-Field-Structure Numerical Analysis of Rock-Filled Steel Cage Under Water

Ye Enli1，Zhou Yihong1,2，Xiao Huanxiong1，Ren Lei3
(1. State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；2. College of Hydraulic and Environmental Engineering，Three Gorges University，Yichang 443002，China；3. College of Engineering and Informatics，National University of Ireland，Galway，Ireland)

An introduction to the status of research in the field of the critical velocity of rock-filled steel cage is described. Considering the deficiencies of studies in the past，a concise formula in which the drag coefficient is the main undetermined parameter is proposed to calculate the critical velocity of rock-filled steel cage. In the formula，cage length，instead of the transformed diameter，is employed. A flume test is also carried out for the cage in the shape of aac××. According to the experimental results，the relationshipbetween the flatness and the stability of the cage under water is analyzed，and the value of drag coefficient under different flatness is obtained. The great influence of friction coefficient on the stability of rock-filled steel cage is also discussed. Besides，for a better understanding of the flow field around the cage，a large eddy simulation is employed to simulate the three dimensional structure of the flow passing a pervious cubic-blunt body at Re=2.2×104. Thus，the characteristics of this kind of flow field and its concrete effects are concluded from the aspects of flow field structure，vortex shedding，drag coefficient and static pressure distribution.

rock-filled steel cage；critical velocity；flume test；flow passing a pervious cubic-blunt body；large eddy simulation

TV131.61

A

0493-2137(2014)02-0108-08

10.11784/tdxbz201206059

2012-06-26；

2012-09-04.

国家“十一五”科技支撑计划项目(2008BAB29B02-2-2).

叶恩立（1987— ），男，博士研究生，yeenli2005@aliyun.com.

周宜红，zyhwhu2003@163.com.