转台分度误差的检定及补偿模型的建立

郭敬滨，曹红艳，王克新，齐永岳(. 天津大学精密测试技术及仪器国家重点实验室，天津 30007；. 温州市计量技术研究院，温州 35000)

转台分度误差的检定及补偿模型的建立

郭敬滨1，曹红艳1，王克新2，齐永岳1
(1. 天津大学精密测试技术及仪器国家重点实验室，天津 300072；2. 温州市计量技术研究院，温州 325000)

用误差补偿的方法提高转台分度精度是一种经济、有效的技术措施，用比较法对转台的分度误差进行了检定，并分析了其测量不确定度；从转台分度误差的来源出发，根据转台分度误差的周期性等特点和谐波分析的结果，并结合最小二乘法、三次样条插值、傅里叶级数拟合3种模型的特点，通过分析，选择傅里叶级数作为转台分度误差的补偿模型，并对3种模型的拟合效果进行了比较．应用傅里叶级数模型对精度为17.82″ 的转台进行补偿，补偿后转台的分度误差最大值为2.36″，从而验证了分度误差模型的正确性和可行性．

分度误差；检定；数据拟合；傅里叶级数；补偿模型

转台是进行圆分度的常用设备，经常作为机床附件进行零件的圆分度加工．为了测量齿轮等回转体零件，也常用到转台．随着科学技术的不断发展，对齿轮测量精度的要求也越来越高[1-2]．转台精度会影响齿轮等回转体零件的测量精度，通过软件误差补偿的方法可以简单、有效地提高转台的精度，以较低的成本达到较高的精度要求．

由于在转台的分度误差中，系统误差占主要成分，从而可以用非实时误差补偿的方法对转台分度误差进行修正，基本思想是以精度更高的仪器作为基准，将转台分度误差先检定出来，选择合适的拟合或插值函数作为转台分度误差的补偿模型，对转台分度误差进行补偿．由此可知，在转台分度误差补偿中，误差的检定和模型的选择将直接影响补偿效果，是分度误差补偿的关键．

针对采用多面棱体检定时受多面棱体面数限制测量间隔不能太小的问题，笔者提出采用多齿分度台与平面反射镜组合构建可回转的多角度基准的检定方法，并对该方法的测量不确定度进行了分析．对采用最小二乘多项式拟合、傅里叶级数拟合和三次样条插值3种补偿模型进行了分析对比，由于分度误差具有周期性特点，采用傅里叶变换的方法建立补偿模型效果更好．

1 分度误差检定及测量不确定度分析

1.1 分度误差来源

转台的分度误差主要包括圆光栅本身的制造误差和机械装配误差等．

制造圆光栅的方法有机械刻画法和光电式刻画法．采用机械法刻画圆光栅时，其刻画误差与圆刻机的蜗轮副误差、传动链误差、调整误差等有关[3]．目前，常采用光电式刻画法，主要有接触式光刻法、接近式光刻法及投影式光刻法[4-5]，光电式刻画法精度高，不受齿轮传动系统误差、蜗轮副的制造偏差等影响，其制造精度与制造工艺有关．圆光栅的制造误差是以2π为周期的函数，因此可以将其展成傅里叶级数，即多次谐波叠加的形式．

装配误差包括圆光栅的安装偏心、倾斜等，安装偏心会引起一次谐波误差，倾斜会引起二次谐波误

差[6-9]．

以上各误差分量都具有周期性，空间基周期为2π，因此，转台的分度误差函数为多次谐波的叠加．

1.2 误差的检定

为了补偿转台的分度误差，首先需要对其进行检定．常用的检定方法是以正多面棱体作为圆分度标准器，用自准直仪进行读数测量．为了提高检定精度，常采用全组合测量法，但全组合测量法工作量大，而且受多面棱体面数的限制，测量间隔不能太小．目前常用的多面棱体面数最多为72面，可达到的最小测量间隔为5°，且一个多面棱体只能实现一种或几种角度间隔的测量．多齿分度台具有较易获得高的分度精度、对使用环境要求不高、操作简便等优点，作为圆分度标准器可以实现较高的精度[10-12]．因此，本文利用多齿分度台与平面反射镜组合，形成一种可回转的多角度基准，能够测量正多面棱体不能实现的角度间隔，且工作量小、精度高．

用多齿分度台检定转台分度误差的基本思想是：以多齿分度台为分度基准件、其回转的角度作为标准角度，转台实际转过的角度与标准角度比较，由光电自准直仪读取角度偏差．其测量原理如图1所示．

多齿分度台安装在转台工作面的中心，平面反射镜固定在多齿分度台上，利用自准直仪进行瞄准．测量时，先将被检转台置零位，读取自准直仪的初始值f0，然后多齿分度台及反射镜随转台一起转动φ角度(φ=360°/n，n为整数，且需满足φ是多齿分度台最小分度间隔的整数倍，实验中采用360齿精密多齿分度台，可实现的最小间隔为1°)，当反射镜随多齿分度台向相反方向回转相同的角度后，光电自准直仪再次瞄准反射镜并读取测量值f1．两次读数之差即为该角度间隔的分度误差Δφ=f1-f0=φ′-φ(其中φ′为转台实际转过的角度)，如此顺序对各被检角度进行测量(记第i个测量点读数为fi)，直至整周．各测量点读数与初始值之差xi(xi=fi-f0)即是转台相对于零位的分度误差．

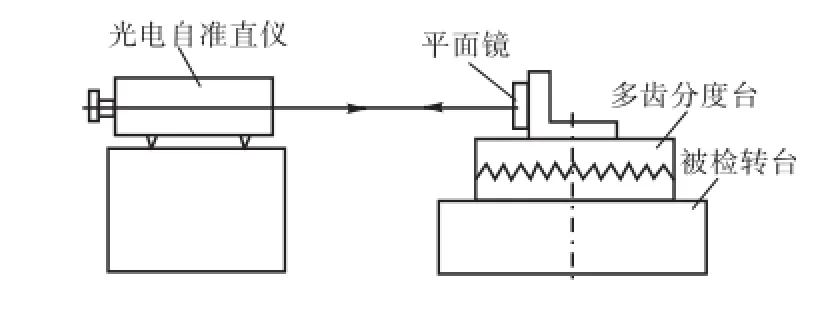
图1 检测装置示意Fig.1 Schematic diagram of detection device

1.3 不确定度分析

当多齿分度台存在安装偏心时，通过分析可知，安装偏心不会引起自准直仪示值变化，仅使光线照射在反射镜上的位置发生了改变ΔL．如果反射镜存在平面度误差，由位置变化引起的误差与反射镜的平面度有关．因此影响测量结果的因素主要有多齿分度台的分度误差和重复性误差、光电自准直仪的示值误差和稳定性误差、反射镜的平面度误差以及外界环境的影响等．

本实验使用的360齿精密多齿分度台分度误差u1=0.3′′，重复性误差u2=0.18′′；双轴光电自准直仪测量精度为u3=0.5′′，重复性误差u4=0.3′′；反射镜反射面宽度H=60,mm，平面度误差δ=λ/8≈0.079 μm，当光线偏离原来位置的距离ΔL=2,mm时，引入的误差u5=8δΔLρ/H2=0.07′′，其中ρ=206265′′，表示1弧度对应的秒值．

由于上述各项不确定度分量相互独立，则合成不确定度(即测量不确定度)为

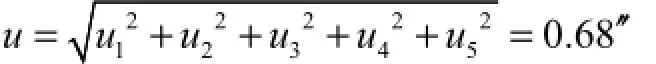
2 分度误差补偿模型的建立

转台分度误差检定后，给出的是一系列离散点的分度误差，而在实施误差修正时，补偿点可能不在测量点上，需要对检定结果进行插值或拟合处理，找出转台的分度误差X与转角θ之间的关系，建立数学模型，从而求得转台任意补偿点处的分度误差．数学上常用的拟合方法有最小二乘法、三次样条法和分段多项式插值等．

最小二乘多项式拟合可以得到较高的精度，表达式唯一，易于计算，但当拟合的曲线比较复杂时，多项式次数高，会产生Runge现象，导致拟合精度较低．因此，对于比较复杂的曲线，不适宜采用最小二乘法多项式拟合．

在用插值算法时，高次多项式插值会产生振荡现象，数值稳定性差，导致插值误差增大；分段低次多项式插值简单、收敛性好，但在节点处光滑性较差．三次样条插值(记为S(θ))不存在这些问题，它在每个子区间[θi,θi+1]上都是3次多项式，即S(θ)=aθ3+bθ2+cθ+d．三次样条插值可以用较低的阶数来对比较复杂的数据进行拟合，并且在节点处具有二阶连续导数，从而可以保证光滑连接．

根据检定得到的各节点处的分度误差，可得插值函数

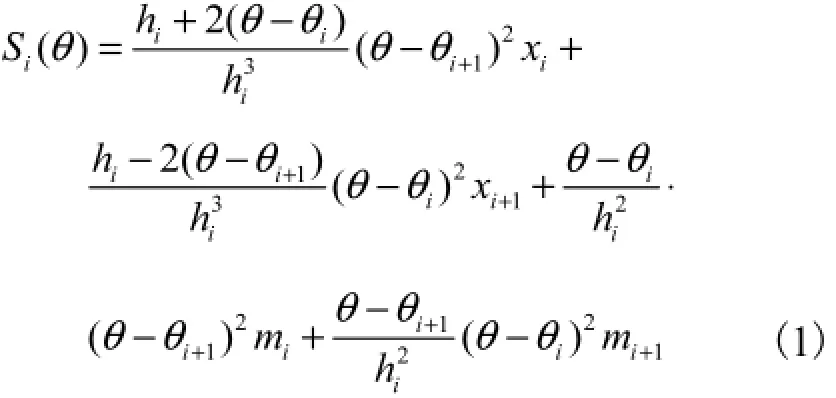
式中：θ为转台转角；θi、θi+1分别为第i、i+1个检定点处的转角；hi=θi+1-θi．以第一类边界条件为例，mi可根据线性方程组(2)求得．

根据检定得到的数据，由式(2)即可求得mi，代入式(1)可得到各子区间[θi,θi+1]上的3次多项式．为了求得转台转角θ处的分度误差，首先要判断θ所在的区间，再将θ代入该区间上的3次多项式即可．

通过以上分析可知，三次样条插值计算过程复杂，且由于在实测数据中总是存在误差，对数据进行三次样条插值，随机误差没有被均化，影响拟合精度.

傅里叶级数是以三角函数表示的无穷级数，特别适合对周期性函数进行描述，在工程技术领域应用广泛[13-15]．设转台的分度误差为()Xθ，由于它是以2,π为周期的函数，根据傅里叶级数展开和收敛定理可知，()Xθ可以展开成傅里叶级数，即

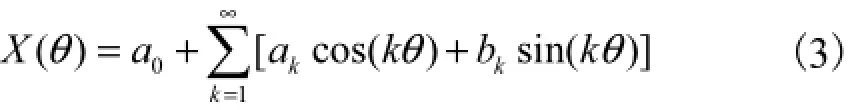
式中：k为谐波次数；a0、ak、bk为傅里叶系数．

式(3)由无限个谐波叠加而成，但由于在实际检定时测量点数n有限，因此只能取有限项谐波叠加来逼近X(θ)．设傅里叶级数拟合中周期项个数为m(m≤[n/2])，则拟合得到的转台分度误差函数F(θ)为

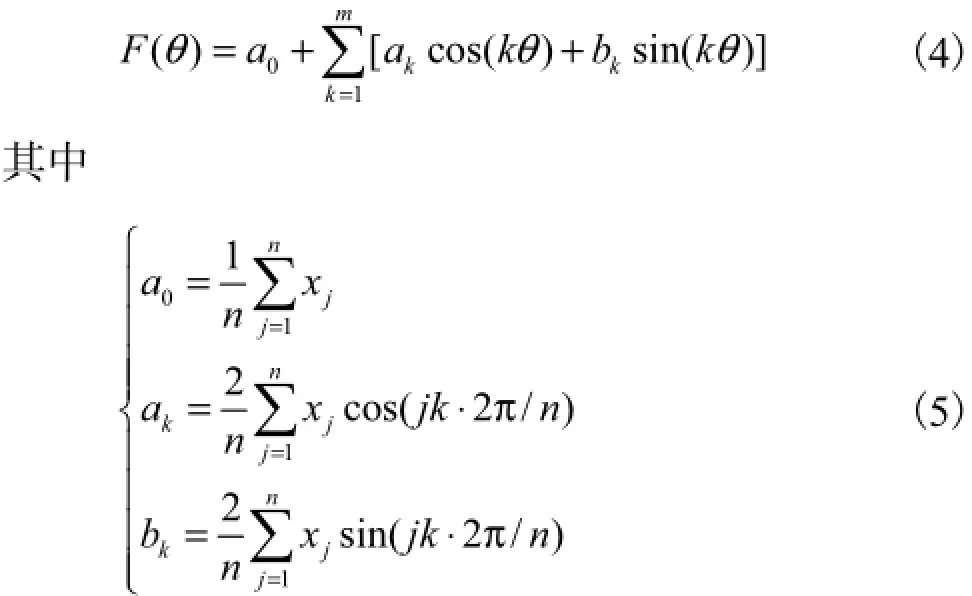
根据测量得到的离散数据，由式(5)求出傅里叶级数拟合方程中各系数，将各次谐波叠加，即可得到连续函数F(θ)．

由式(4)和式(5)可知，傅里叶级数拟合模型计算过程简单，能很好地反映数值的周期现象，对复杂曲线的拟合能力强；根据拟合函数中各次谐波的幅值大小，可以为加工者寻找、分析误差源，也可为使用者寻求最佳使用方法提供有用的信息，而且傅里叶级数拟合可以抑制测量数据中随机误差的影响．在拟合过程中由于m的取值受测量点数n的限制(m≤n/2)，因此，拟合精度与n有关，当精度要求较高时，需要通过适当增大n值来获得较高的拟合精度．

通过以上的分析可知，3种模型各有优缺点，实际应用时应根据拟合对象的特点来选择合适的拟合模型．

误差检定时选定测量间隔为5°，测量得到的离散数据及经谐波分析得到的各次谐波幅值大小如图2所示．

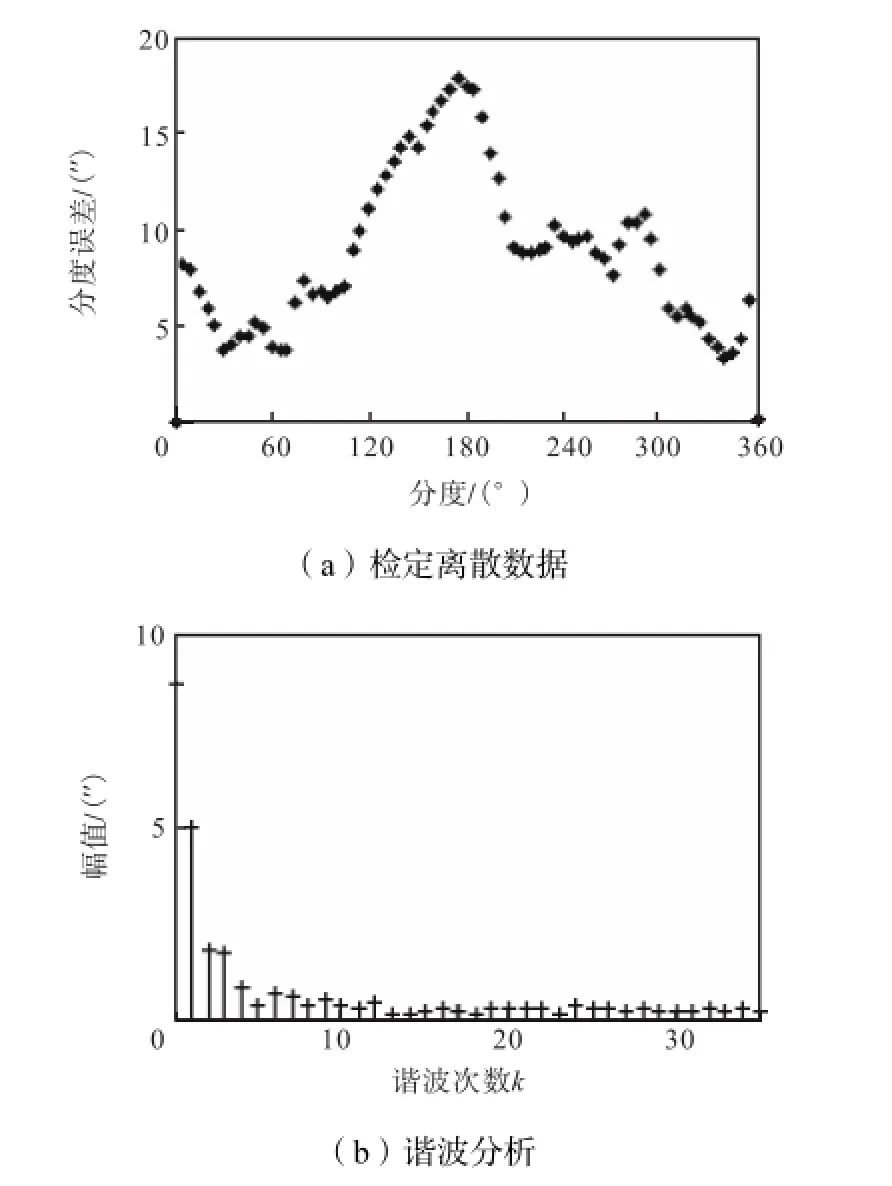
图2 转台分度误差检定结果Fig.2 Test results of indexing error

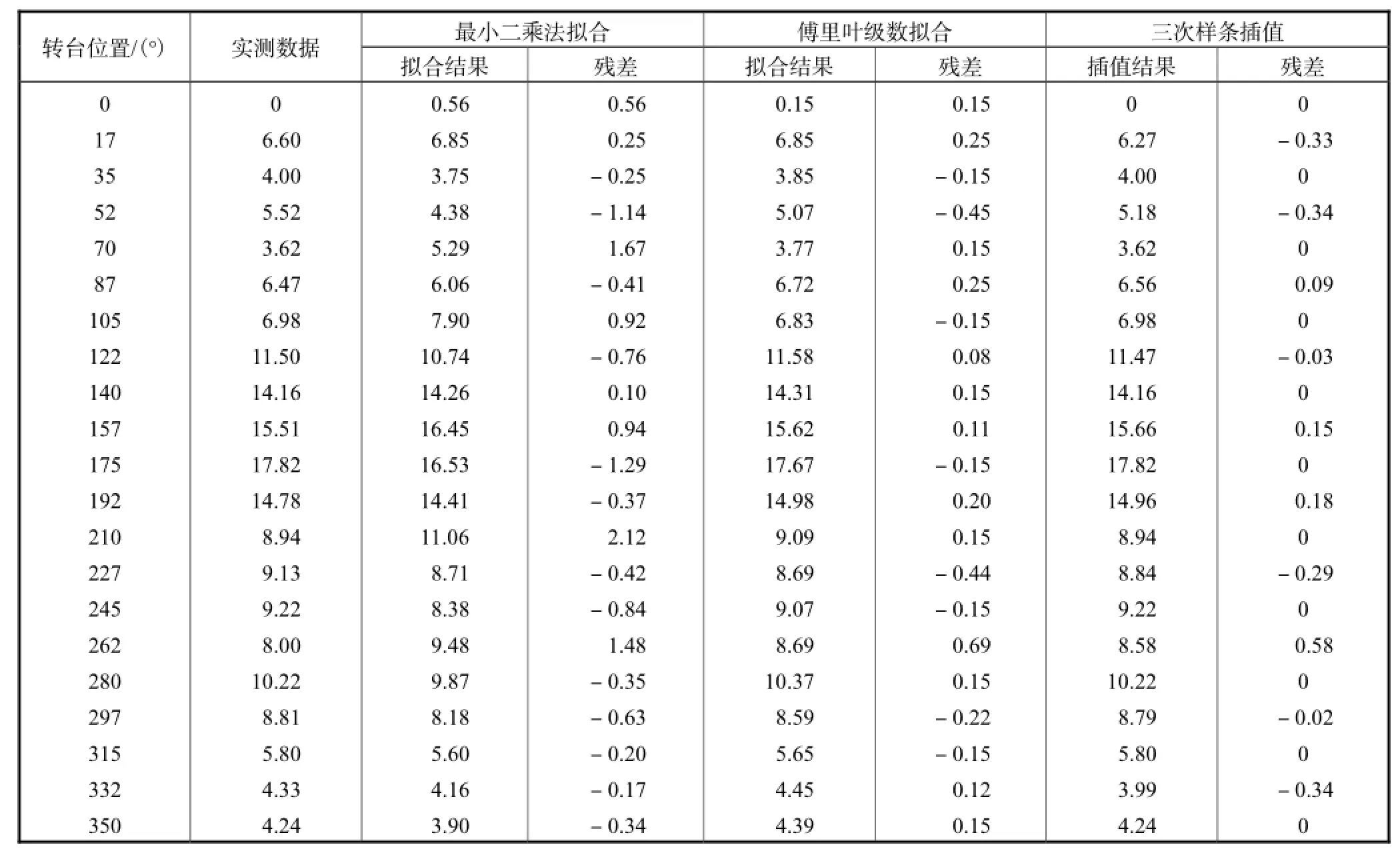
表1 3种模型拟合结果对比Tab.1 Comparison of three kinds of fitting models (″)

由图2可知，检定得到的离散数据比较复杂，因此，不适宜采用最小二乘多项式拟合．转台分度误差为周期函数，是以2π为基周期的多次谐波的叠加，而三次样条插值不能反映数据的周期性．由图2(b)谐波分析结果可以看出，转台分度误差以低次谐波为主，由于傅里叶级数适用于对周期函数进行描述，对复杂曲线的拟合能力强，针对转台分度误差的周期性、误差来源以及数据的复杂程度等特点，选择傅里叶级数作为转台分度误差的拟合模型．

为了验证傅里叶级数拟合方法的有效性和可行性，本文针对检定数据分别建立了转台分度误差的最小二乘多项式拟合模型、傅里叶级数拟合模型和三次样条插值模型，并对它们的拟合效果进行了比较．

为了使比较具有一般性，从0°起每隔18°或17°选取比较点，从而使选取的点既包括检定点也包括中间点．分别根据3种模型计算各点的分度误差值，与实测得到的数据对比，求得各点的残差，数据见表1，残差曲线如图3所示．

拟合精度由残差平方和来评定，认为残差平方和越小，曲线的拟合效果越好[15]．通过计算求得最小二乘法拟合残差平方和为17.08，傅里叶级数拟合为1.35，三次样条插值为0.83．通过对比可以看出，傅里叶级数比最小二乘多项式拟合精度高，与三次样条插值模型的拟合结果很接近．由于三次样条插值函数需要求解线性方程组，且对于给定的θ角，需要判断θ所在的区间，计算过程复杂[16]；傅里叶级数拟合中，根据式(5)可求得各次谐波的系数，再将θ代入式(4)求解即可得到转台转角为θ时的分度误差，易于计算，且能体现分度误差的周期性，因此，选择傅里叶级数()Fθ作为转台分度误差的拟合模型，是一种简单有效的数据处理方法．

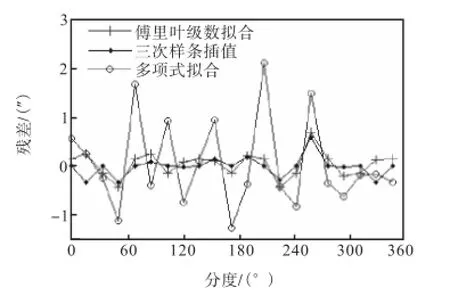
图3 残差曲线Fig.3 Residual curves

3 实验验证

在对分度误差进行检定和拟合完成以后，就可以对其进行补偿．误差补偿后对转台的分度误差进行5次测量，并对转台反转时的补偿效果进行了实验．补偿前后的分度误差曲线如图4所示(补偿后测量点数n为144)．可以看出，补偿前转台的分度误差最大值为17.82''；补偿后正转和反转时分度误差大部分分布在±0.5"之间，且具有随机性，与补偿之前相比，定位精度得到了明显的改善．5次测量中最大分度误差的平均值为2.36''，重复性标准差(用实验标准偏差表示)σ=0.40"．该重复性误差是由转台本身的重复性、测角系统的重复性误差(包括自准直仪读数重复性、多齿分度台测角重复性等)以及环境等因素引起的．通过以上的分析可知，该补偿方法对转台正、反转时都适用，且重复性较好．

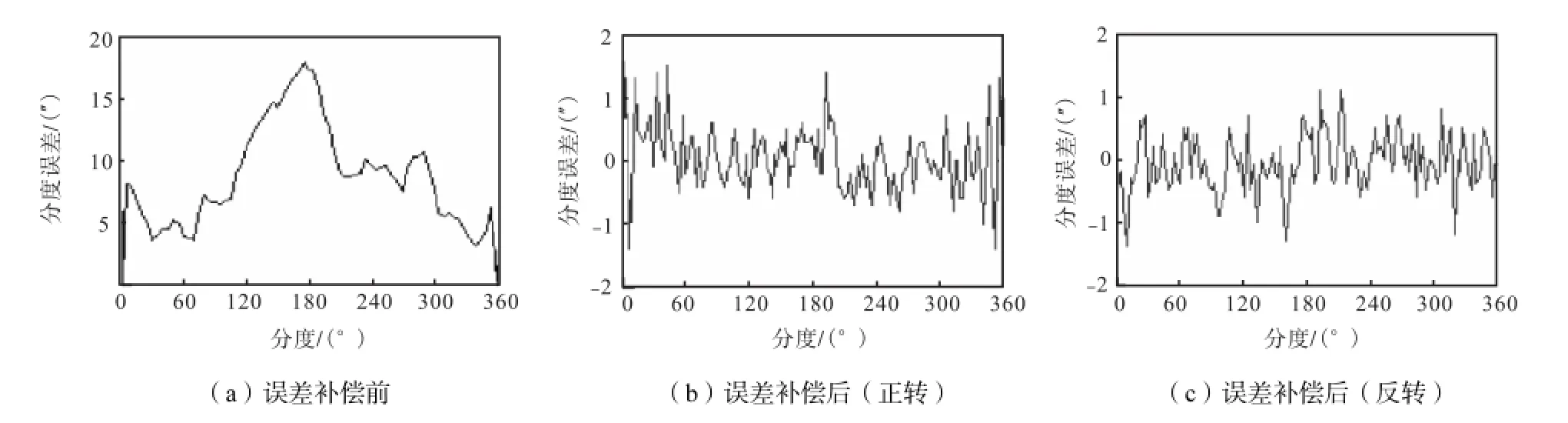
图4 误差补偿效果Fig.4 Effect of error compensation

4 结 语

本文对转台分度误差的来源进行了分析，利用多齿分度台和双轴光电自准直仪对转台的分度误差进行检定，根据谐波分析的结果和分度误差的周期性等特点以及数据的复杂程度，选择傅里叶级数拟合作为转台分度误差的补偿模型．与其他两种模型相比，该模型计算简单且适用于对周期性函数的描述．对3种模型的拟合效果进行对比，结果表明，傅里叶级数具有较高的拟合精度．最后，对转台分度误差进行补偿实验，补偿后效果很好，大大提高了转台的分度精度，从而验证了分度误差模型的合理性和正确性．

［1］ 郭敬滨，张大厦，张继承. 大齿轮齿形测量中补偿安装偏心的理论分析[J]. 天津大学学报，2012，42(5)：435-439. Guo Jingbin，Zhang Dasha，Zhang Jicheng. Compensation theory analysis of installation eccentricity in measurement of large gear tooth[J]. Journal of Tianjin University，2012，42(5)：435-439(in Chinese).

［2］ 郭敬滨，王 娴，刘海军，等. 摆线齿轮误差的测量及修形量计算[J]. 天津大学学报，2011，44(1)：85-89. Guo Jingbin，Wang Xian，Liu Haijun，et al. Measurement of cycloidal gear error and calculation of modification[J]. Journal of Tianjin University，2011，44(1)：85-89(in Chinese).

［3］ 杨永才，陈 林，孙银春，等. 圆光栅刻划误差的自动校正[J]. 华东工业大学学报，1996，18(3)：85-90. Yang Yongcai，Chen Lin，Sun Yinchun，et al. Auto-matic correction for dividing errors of radial grating [J]. East China University of Technology，1996，18(3)：85-90(in Chinese).

［4］ 曹天宁，周鹏飞. 光学零件制造工艺学[M]. 北京：机械工业出版社，1987. Cao Tianning，Zhou Pengfei. Optical Parts Manufacturing Technology [M]. Beijing：China Machine Press，1987(in Chinese).

［5］ 曹向群，黄维实，金 彤. 光栅计量技术[M]. 杭州：浙江大学出版社，1992. Cao Xiangqun，Huang Weishi，Jin Tong. Grating Measurement Technology[M]. Hangzhou：Zhejiang University Press，1992(in Chinese).

［6］ 赵人杰，马文礼. 利用误差谐波补偿法提高金属圆光栅测角精度[J]. 仪器仪表用户，2009，16(3)：69-71. Zhao Renjie，Ma Wenli. Improving the accuracy of newtype encoders using error harmonic compensation [J]. Instrumentation Customer，2009，16(3)：69-71(in Chinese).

［7］ 黄宗升，秦石乔，王省书，等. 光栅角编码器误差分析及用激光陀螺标校的研究[J]. 仪器仪表学报，2007，28(10)：1866-1869. Huang Zongsheng，Qin Shiqiao，Wang Xingshu，et al. Error analysis of optical angular encoder and its calibration with ring laser gyro [J]. Chinese Journal of Scientific Instrument，2007，28(10)：1866-1869(in Chinese).

［8］ 张礼松，管炳良. 关节坐标测量机研制中圆光栅误差修正技术[J]. 计测技术，2007，27(4)：41-43，69. Zhang Lisong，Guan Bingliang. Error correction and its application to multi-joint CMM research [J]. Measuring Technique，2007，27(4)：41-43，69(in Chinese).

［9］ Qin Shiqiao，Huang Zongsheng，Wang Xingshu. Optical angular encoder installation error measurement and calibration by ring laser gyroscope [J]. Instrumentation and Measurement，2010，59(3)：506-511.

［10］ Hatiris E，Orton P A，Poliakoff J F，et al. Eccentricity error compensation models for an incremental motion encoder[C]//Proceedings of the 16th European Simulation Multiconference on Modelling and Simulation 2002. Darmstadt，Germany：ESM，2002：328-331.

［11］ 《角度计量》编写组. 角度计量[M]. 北京：中国标准出版社，1984. Compilation Group of 《Angle Measurement》. Angle Measurement [M]. Beijing：The Standards Press of China，1984(in Chinese).

［12］ Kaul S K，Tickoo A K，Koul R，et al. Improving the accuracy of low-cost resolver-based encoders using harmonic analysis[J]. Nuclear Instruments and Methods in Physics Research Section A：Accelerators，Spectrometers，Detectors and Associated Equipment，2008，586(A)：345-355.

［13］ 李友峰. N次谐波法拟合供油凸轮型线的探讨[J]. 内燃机车，2006，386(4)：15-17. Li Youfeng. Study for Nth harmonic method fitting fuel cam profile [J]. Diesel Locomotive，2006，386(4)：15-17(in Chinese).

［14］ Mahmoud F. Harmonic analysis and applications [J]. Kybernetes，2012，41(1)：129-144.

［15］ 魏玉业，赵凤阳. 曲线最佳拟合的评价标准[J]. 测绘科学，2010，35(1)：195-196. Wei Yuye，Zhao Fengyang. The evaluation criteria of optimal curve fitting [J]. Science of Surveying and Mapping，2010，35(1)：195-196(in Chinese).

［16］ 高贯斌，王 文，林 铿，等. 圆光栅角度传感器的误差补偿及参数辨识[J]. 光学精密工程，2010，18(8)：1766-1772. Gao Guanbin，Wang Wen，Lin Keng，et al. Error compensation and parameter identification of circular grating angle sensors [J]. Optics and Precision Engineering，2010，18(8)：1766-1772(in Chinese).

(责任编辑：赵艳静)

Check of Indexing Error for Turntable and Establishment of Its Compensation Model

Guo Jingbin1，Cao Hongyan1，Wang Kexin2，Qi Yongyue1
(1. State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China；2. Wenzhou Institute of Measurement Technology，Wenzhou 325000，China)

Error compensation method is an economical and effective technical measure to improve the indexing accuracy for turntable. The indexing error was checked by comparison method，and the measurement uncertainty was also analyzed in this paper. According to the periodicity of indexing error and the harmonic analysis results，and combined with the characteristics of least square method，cubic spline interpolation and Fourier series，this paper chooses Fourier series as the compensation model for turntable indexing error and compares the fitting effects of the three models. By using the Fourier series，the maximum indexing error is 2.36″ after compensation the turntable with 17.82″，which has verified the validity and feasibility of the compensation model.

indexing error；check；data fitting；Fourier series；compensation model

TB922

A

0493-2137(2014)06-0524-06

10.11784/tdxbz201207027

2012-07-09；

2012-10-12.

天津市自然科学基金资助项目(10JCYBJC06600).

郭敬滨（1959— ），男，副教授.

郭敬滨，guojingbin@tju.edu.cn.