斜拉索表面水膜形态及斜拉索气动力变化规律

毕继红，王 剑，逯 鹏，鲍 春(. 天津大学建筑工程学院，天津 30007；. 滨海土木工程结构与安全教育部重点实验室，天津 30007)

斜拉索表面水膜形态及斜拉索气动力变化规律

毕继红1,2，王 剑1，逯 鹏1，鲍 春1
(1. 天津大学建筑工程学院，天津 300072；2. 滨海土木工程结构与安全教育部重点实验室，天津 300072)

斜拉索表面水线的形成与振荡是斜拉索发生风雨激振的重要原因之一．为研究水线运动与风雨激振现象间的内在联系，本文将滑移理论与计算流体力学相结合，考虑斜拉索表面水膜形态对风压力系数和风摩擦力系数的影响，建立了一个模拟风雨条件下斜拉索表面水膜形态变化的理论模型；在此模型基础上推导出风雨作用下斜拉索气动力计算公式，通过数值模拟得到不同风速下的斜拉索表面水膜形态及气动力变化规律，分析二者间的内在联系．与已有的试验结果对比发现：当斜拉索发生风雨激振现象时，水线形态变化与气动力变化频率相同，且接近拉索的自振频率，说明风雨激振现象的产生原因是水线形态的周期性变化引起拉索的共振．

风雨激振；斜拉索；水线；水膜；气动力；滑移理论

风雨激振是指斜拉桥拉索或拱桥吊杆在风雨条件下发生的一种低频大幅度振动[1]．各国研究人员多次在野外观测到风雨激振现象[2-4]，并通过一系列风洞试验[5-8]再现了这一现象，发现斜拉索表面水线的形成和振荡是产生风雨激振现象的关键因素．

由于观测技术的限制，作用在斜拉索上的气动力难以通过现场观测或风洞试验测得，已有的理论模型中的拉索气动力都进行了一定程度的假设和简化[9-13]，无法准确反映不同水线形态下拉索的气动力；而斜拉索风雨激振现象涉及到气、液、固三相耦合，且气动力分析是揭示风雨激振现象形成机制的重要手段，因此有必要精确求得风雨作用下的斜拉索气动力．本文在Lemaitre等[14]的水膜计算模型基础上，推导出斜拉索的气动力，为今后建立水膜运动和斜拉索振动的耦合模型提供重要的理论依据．考虑拉索倾角和风偏角，将滑移理论与计算流体力学软件Fluent相结合，通过数值求解得到不同风速下斜拉索表面水膜形态及拉索气动力变化规律；将计算结果与前人的试验[7]及数值模拟结果[15]进行比对以验证模型的合理性；在此基础上研究水膜形态与拉索气动力间的内在联系，揭示风雨激振现象的产生机理．

1 模 型

1.1 基于滑移理论的水膜运动方程

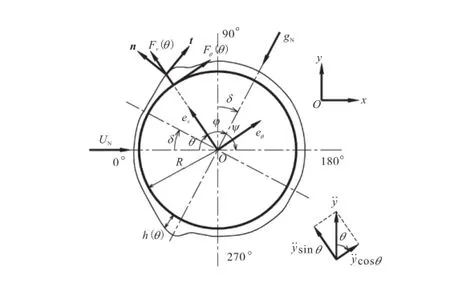
考虑半径为R、水平倾角为α(0°≤α≤90°)的拉索受水平方向风力和重力的共同作用，如图1所示，风速为U0，风偏角为β(0°≤β≤90°)，风攻角为0°．

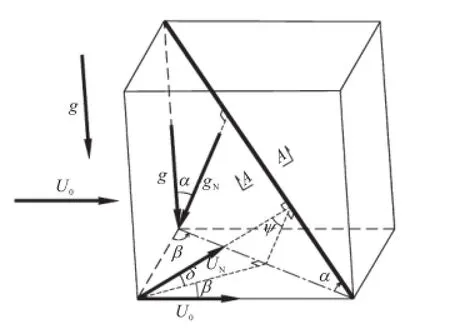
图1 斜拉索空间姿态Fig.1 Schematic diagram of the inclination angle and wind yaw angle of cable

取图1中的斜拉索A-A断面为研究对象，其表面上的水膜受力如图2所示．

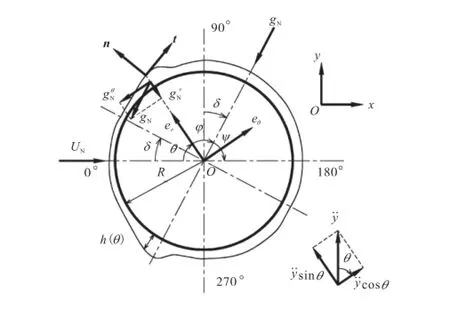
图2 斜拉索表面水膜受力Fig.2 Force of water film around cable

忽略重力沿拉索轴向的分量，则作用在拉索断面内的重力分量Ng为

采用准定常假设，忽略轴向流的影响，只考虑垂直于斜拉索的气流作用，则拉索断面内的风速NU为

NN

根据滑移理论，假设拉索表面存在一层连续的水膜，极坐标系(er,eθ)下水膜内任一点的坐标为(r,θ)，R≤r≤R+h，水膜厚度为h(θ,t)，h＞0，水膜内的流场速度u可表示为分量形式u=urer+uθeθ，则无量纲化的流场速度分布为

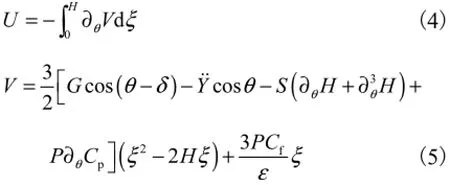
无量纲化的水膜运动方程可表示为

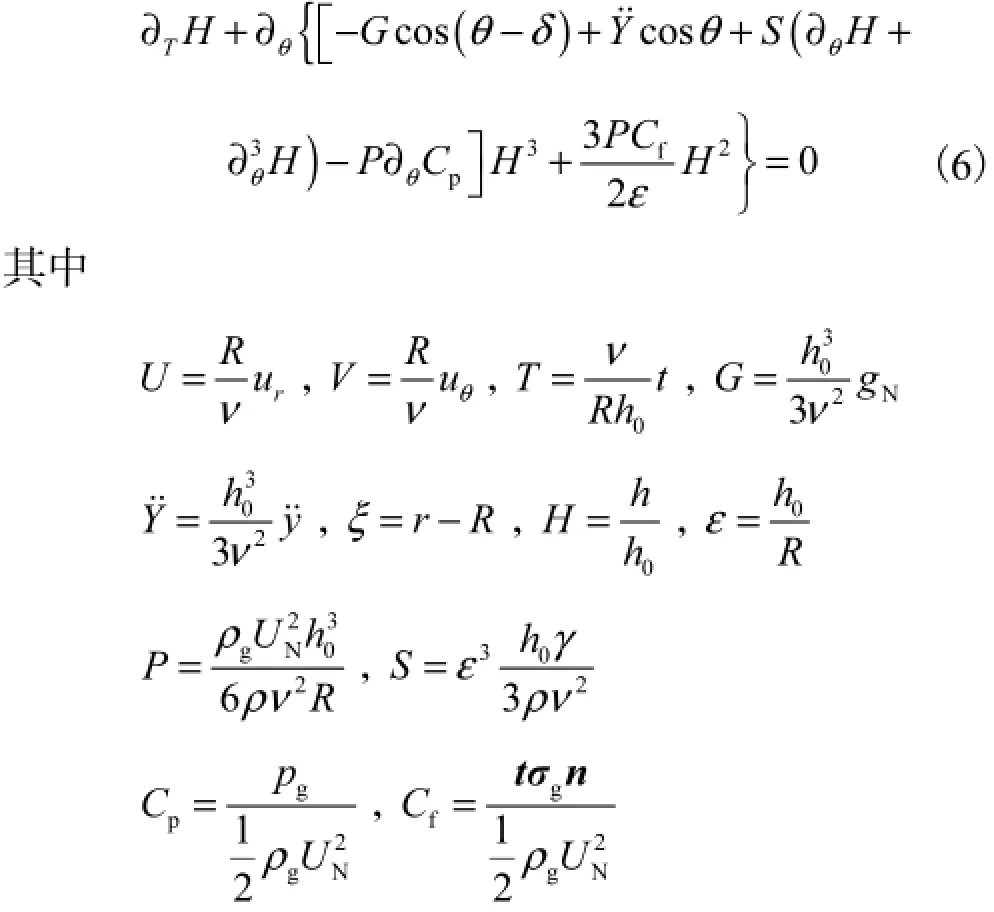
式中：n和t分别为水膜表面的法向量和切向量；gσ为空气应力张量；γ为水在空气中的表面张力系数(γ与θ无关)；gρ为空气密度；gp为水膜表面所受的空气压力；ρ为水膜的密度；p为水膜内的压强；ν为水的运动黏性系数．

推导过程详见文献[14]．

1.2 斜拉索断面的气动力

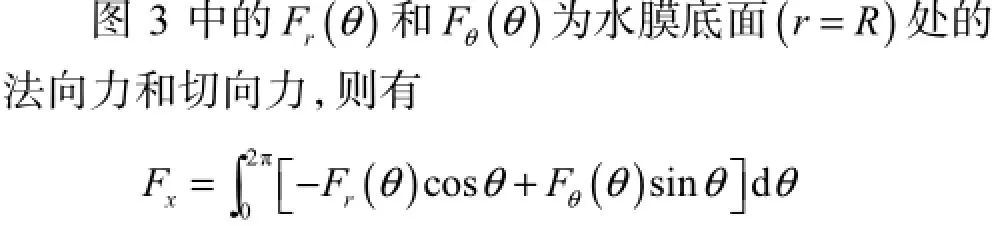
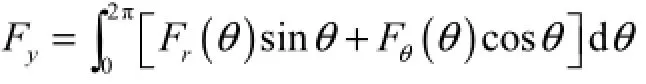
式中xF和yF分别为风雨作用下斜拉索断面的顺风向阻力和横风向升力．

水膜底面的应力张量为

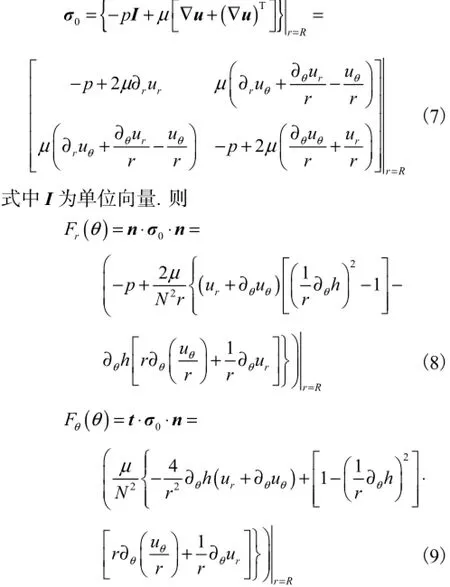
将式(6)定义的无量纲参数分别代入式(8)和式(9)，化简后得到无量纲的法向力和切向力

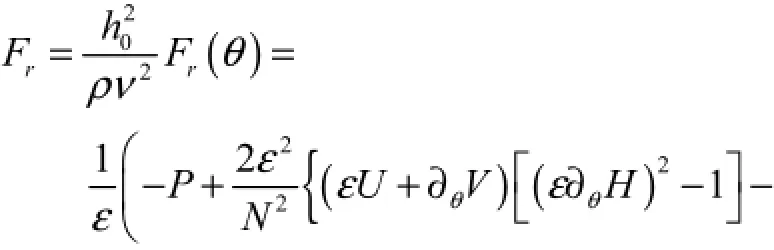
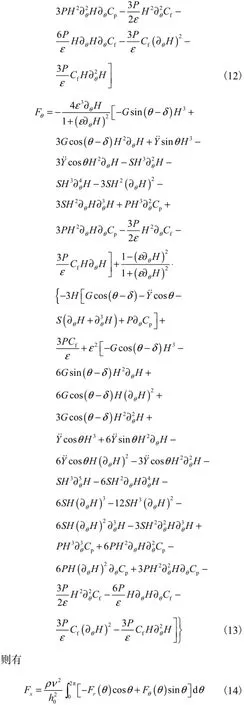
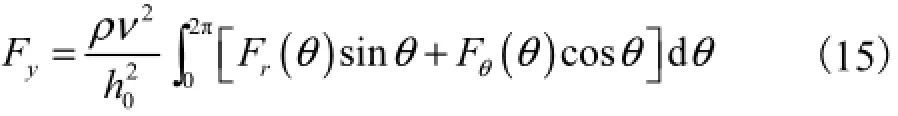
2 数值求解

2.1 风压力系数Cp和风摩擦力系数Cf的确定

水膜运动方程中的风压力系数Cp和风摩擦力系数Cf是影响水膜运动的关键参数．Lemaitre等[14]在求解方程时采用由Achenbach[16]通过试验确定的表面光滑、干燥的圆柱体的风压力系数Cp和风摩擦力系数Cf，由于Cp和Cf是固定不变的，导致迭代求解方程只能得到上、下水线的初始形成位置，而不能模拟水线在斜拉索表面的运动．由于风雨激振中斜拉索表面水膜形态随时都会发生变化，求解方程时需要确定每一时刻的风压力系数Cp和风摩擦力系数Cf分布；而现阶段已有的研究成果只是对光滑索面及在某些特定位置固定了人工水线的拉索的风压力系数Cp和风摩擦力系数Cf进行风洞试验[17]和数值模拟[18]，无法满足求解水膜运动方程的需要，只有采用参数化的数值模拟方法才能求得任一时刻任意水膜形态的Cp和Cf，进而模拟水膜形态的变化．

下面对这一方法进行简要介绍并进行验证．本文仍采用Lemaitre等[14]的假设，即假设作用在水膜上的风荷载与作用在干燥拉索表面的风荷载相等．采用Fluent软件，将水膜考虑为固体(柱体)置于定常流场中进行数值模拟．设拉索直径为d，计算区域取边长为18d×12d的矩形加上半径为6d的半圆，将柱体中心置于坐标原点，柱体中心距离入口6d，距离出口18d，距离上下边界6d，采用Gambit软件划分网格如图4所示．

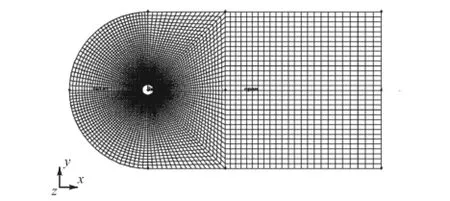
图4 流场网格Fig.4 Numerical grids of flow field

计算区域的边界条件如下：

(1) 来流面(入口)和上下边界均采用速度入口边界条件(velocity-inlet)u=UN，v=0；

(2) 出流面(出口)采用压力出口边界条件(pressure-outlet)p=0；

(3) 柱体表面采用壁面(wall)，即无滑移边界条件u=0，v=0．

应用准定常假设，采用定常流计算，选用k-ωSST过渡流模型和压力求解器(pressure based slover)，压力梯度的计算采用基于单元的最小二乘法(cell-based least squares)，控制方程使用基于单元中心的有限体积法离散，速度-压力耦合使用Coupled算法，对流项应用二阶迎风差分格式，扩散项应用二阶中心差分格式，湍动能k输运方程和耗散率ω输运方程均采用二阶迎风差分格式．

为验证应用数值方法求得Cp和Cf的合理性，将应用Fluent软件计算的结果与Achenbach[16]、Fage和Falkner[19]的实验数据及Celika和Shaffer[20]的数值计算结果进行对比．考虑圆柱直径d=0.16m、风速U=10m/s 的情况，此时的雷诺数Re=≈1×105.Ng图5为Reg=1×105时的圆柱表面风压力系数Cp和风摩擦力系数Cf分布．可以看出，应用Fluent软件计算得到的Cp和Cf与前人的实验数据及数值计算结果比较接近，说明这一方法切实可行．

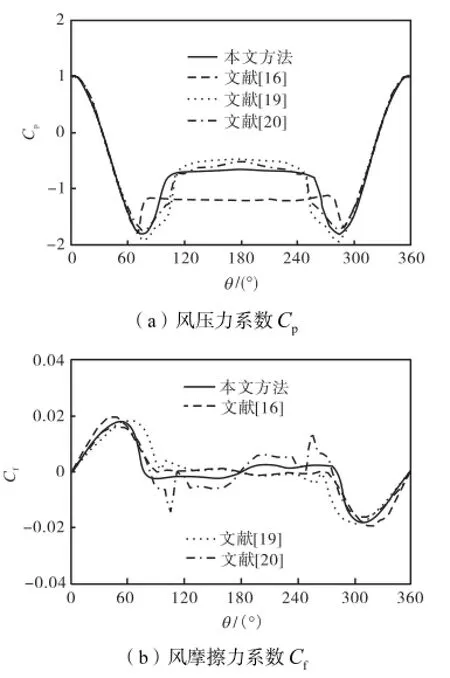
图5 Reg=1×105时的圆柱表面风压力系数Cp和风摩擦力系数Cf的分布Fig.5 Distribution of wind pressure coefficient Cpand friction coefficient Cfaround cylinder when Reg=1×105

下面将应用计算流体力学方法求得的同一风速下拉索表面有、无水线存在时的pC和fC进行对比，有水线的拉索断面如图6所示，上、下水线位置是任意选取的，分别位于θupper=55°和θlower=278°．

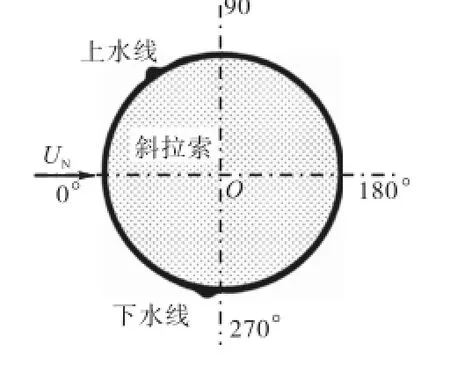
图6 带有上、下水线的拉索断面Fig.6Cross- section of stay cable with upper and lower rivulets

从图7所示的Cp和Cf分布对比可以发现，Cp和Cf在上、下水线位置附近均发生显著变化，这进一步说明在求解水膜运动方程时考虑Cp和Cf随水膜形态的变化是十分必要的．

图7 拉索表面有、无水线时的风压力系数Cp和风摩擦力系数Cf分布对比Fig.7Comparison of wind pressure coefficient Cpand friction coefficient Cfof cable with and without rivulets

2.2 基本参数及数值求解流程

图8显示了用Matlab软件数值求解水膜运动方程式(6)并计算斜拉索受力及用Fluent软件计算风压力系数pC和风摩擦力系数fC的基本流程．

计算pC和fC时用Gambit软件划分流场网格，在这一过程中需要用到前一时刻的水膜形态，因此在划分网格时需进行参数化处理；应用Fourier级数将通过Fluent软件计算的Cp和Cf拟合成连续函数Cp(θ)和Cf(θ)；水膜运动方程式(6)为四阶非线性偏微分方程，采用拟谱法进行数值求解，即在空间上采用Fourier谱方法，在时间上采用四阶Runge-Kutta法；应用数值积分方法按照式(15)计算水膜运动对拉索的升力Fy．将水膜在圆周空间上离散为N=128个点，并选取无量纲化的时间步长dT =5×10-6(dt=5× 10-5s)．初始条件为h(0,θ)=h，即H(0,θ)=1.计算中

0假设水膜质量守恒，并根据Li等[7]的试验设定水膜初始厚度h0=0.2mm，最大厚度hmax=1.0mm；为保证水膜的连续性，设定水膜的最小厚度hmin= 0.02mm.忽略斜拉索运动对水膜形态变化的影响，即˙y=0．其他基本参数详见表1．

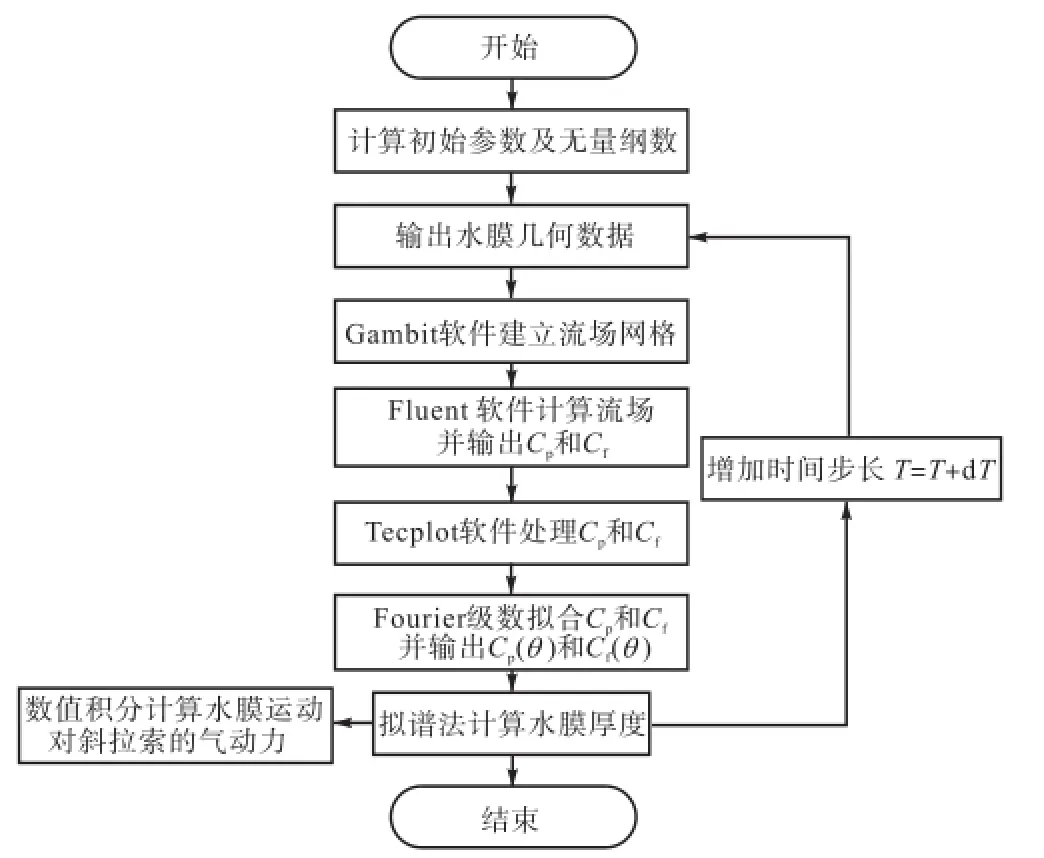
图8 数值计算流程Fig.8 Flow chart of numerical calculation

表1 数值计算基本参数Tab.1 Parameters for numerical calculation

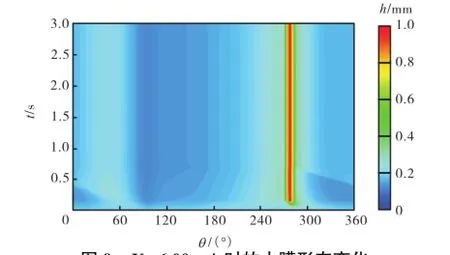
图9 U0=6.00 m/s时的水膜形态变化Fig.9 Temporal evolution of water film morphology when U0=6.00 m/s

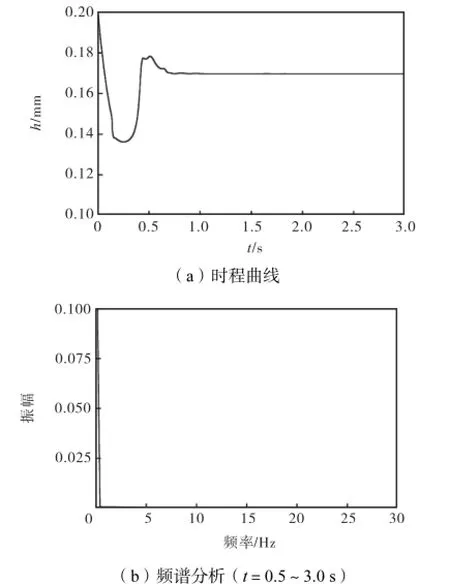
图10 U0=6.00 m/s 时=0°θ位置处的水膜厚度Fig.10Water-film thickness at the position of =0°θ when U0=6.00 m/s

2.3 计算结果

根据已有研究成果[21]，只有当风向与斜拉索的下倾方向一致且风速处于某一特定区域内时才会产生风雨激振现象．在Li等[7]的试验中发生风雨激振时风速范围是U0=6.76～8.04 m/s ，许林汕等[8]也进行类似试验并得到相同结果．对此，本文分别选取U0=6.00m/s 、U0=7.40m/s 、U0=7.72m/s和U0= 9.00m/s4种工况进行数值计算，分析不同风速条件下的水膜形态变化及其引起的斜拉索气动力变化规律.

2.3.1 U0=6.00m/s时

图9为U0=6.00ms 时t=0～3.0s 内的水膜形态变化．水膜在重力、表面张力及气流的作用下逐渐积聚，于t=0.14s前后在θ≈278.4°附近形成下水线，高度约为1.0,mm，宽度约为7.4,mm；由于风速较小，水膜在迎风侧上部的积聚并不显著，没有形成明显的上水线．在t=0.14～0.66s 时间段内有一微小水膜受重力作用自θ≈60°处向迎风侧滑落，最终同下水线汇合到一起，图10所示的θ=0°位置处的水膜厚度变化很好地显示了这一过程．

从图11所示的拉索气动力变化可以看出，阻力Fx和升力Fy的变化趋势基本一致：其在t=0～0.14s内的变化是由于下水线的形成导致的；而在t=0.14～0.66s内发生变化则是因为从上水线分离出一部分水线并与下水线汇合；至t=0.66s 后由于水膜形态保持稳定，阻力Fx和升力Fy均趋于定值．

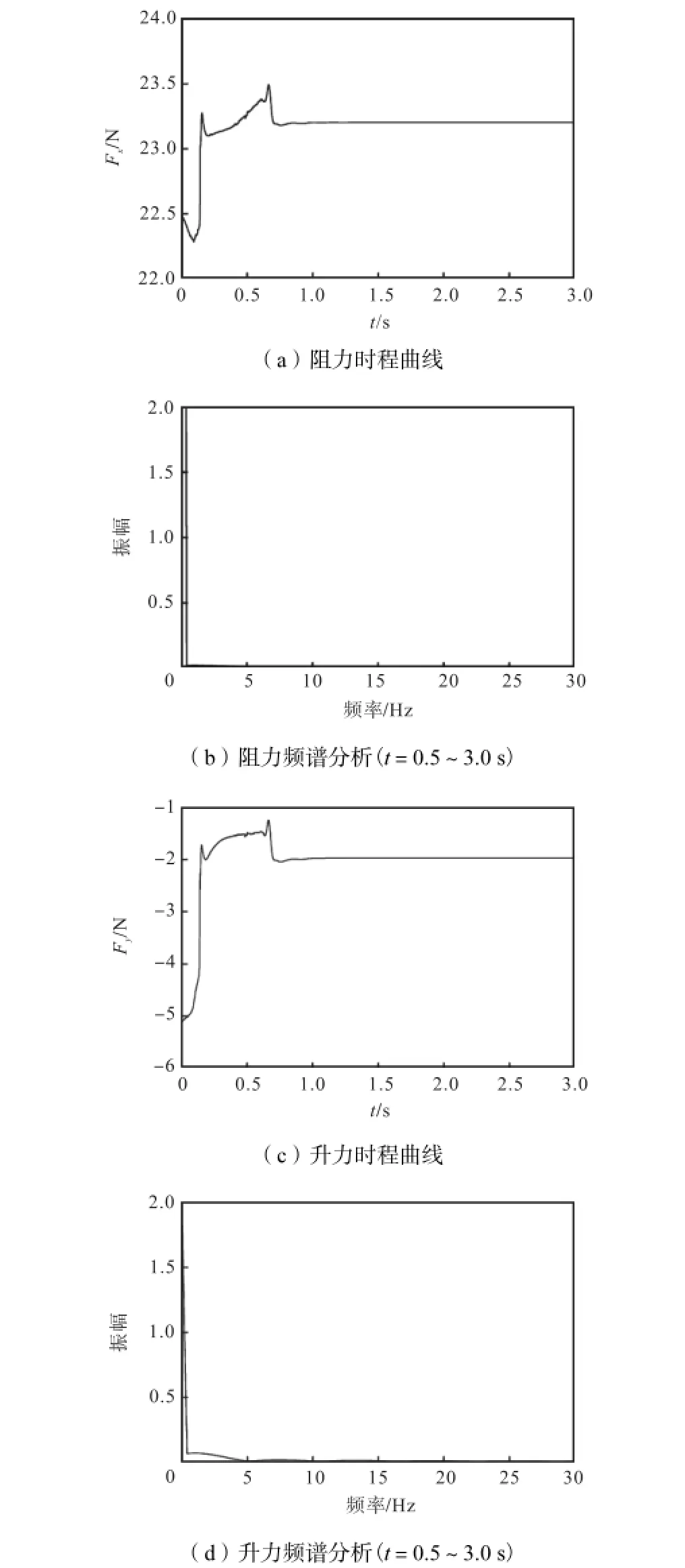
图11 U0=6.00m/s 时的拉索气动力Fig.11 Aerodynamic force of cable when U0=6.00m/s

2.3.2 U0=7.40m/s 时

图12为U0=7.40 ms时的水膜形态时程变化．随着风速的加大，斜拉索表面的水膜形态变化规律与前几个工况相比有了明显变化．下水线在t=0.10 s 时形成于θ≈279.8°处，而后在θ=270.0°～281.3°范围内振荡，最大高度为1.0 mm，宽度变化范围为b=7.4～9.8 mm．气流产生的风压力和风摩擦力使得水膜在迎风侧逐渐积聚，但由于重力作用仍大于气流作用，这部分水膜并未形成稳定的上水线，而是沿迎风侧向下滑落，并不断重复出现这一现象．

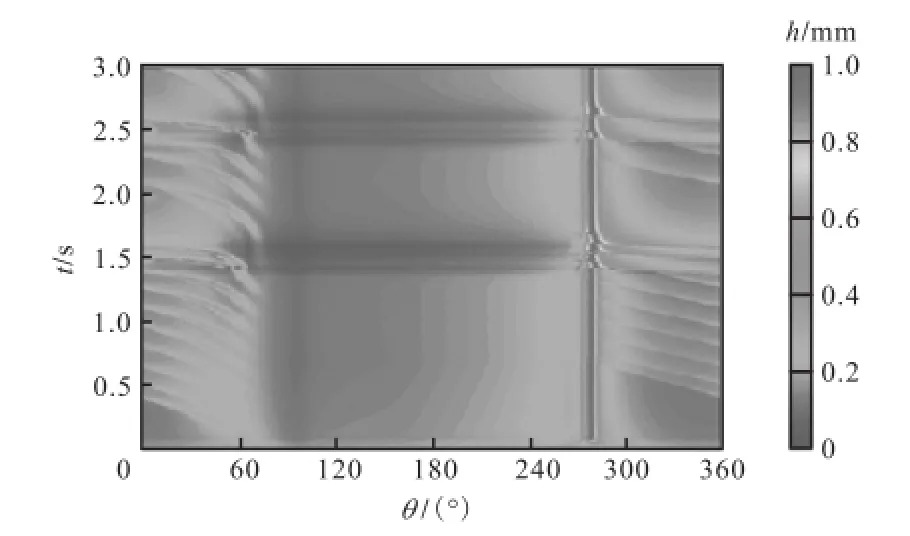
图12 U0=7.40ms时的水膜形态时程变化Fig.12Temporal evolution of water film morphology whenU0=7.40ms

为研究水膜形态随时间变化的规律，选取θ=0°处的水膜厚度变化作为研究对象．随着水线不断向下滑落，θ=0°处的水膜厚度发生显著变化，如图13(a)所示．对t=0.5～3.0 s 内的水膜厚度时程变化曲线进行频谱分析(见图13(b))，发现其振荡主频为f1≈0.800Hz和f2≈3.998 Hz ，分别接近试验中斜拉索的一阶和四阶自振频率．

U0=7.40 ms时的斜拉索气动力变化如图14所示，在上水线形成之前斜拉索气动力的变化与U0=6.00 ms时基本一致，但自t=0.43 s 前后开始不断有水线从迎风侧向下滑落并与下水线汇合，使得斜拉索气动力发生显著变化，对t=0.5～3.0s内的阻力和升力时程变化曲线进行频谱分析(见图14(b)和14(d))，可以看出阻力和升力的振荡频率分别为fx≈1.200 Hz 和fy≈0.800 Hz ，与Li等[15]在风洞试验基础上采用子结构法数值模拟得到的气动力频率相近，进一步证实了这一方法的合理性．升力的振荡频率与θ=0°处的水膜厚度振荡频率相同，说明升力的周期性振荡与水线从迎风侧向下滑落并与下水线汇合现象的周期性出现有密切联系．由于U0=7.40 ms位于风洞试验中发生风雨激振现象的显著风速范围内[7-8]，而升力及水线形态变化的频率与斜拉索的自振频率比较接近，说明风雨激振现象的产生是由于水线形态的周期性变化导致斜拉索气动力的周期性变化，进而导致斜拉索发生共振．

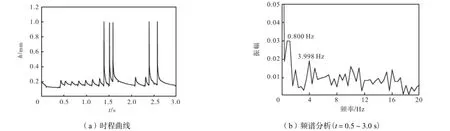
U0=7.40ms时=0°θ位置处的水膜厚度Fig.13Water-film thickness at the position of =0°θ when图13 U0=7.40ms

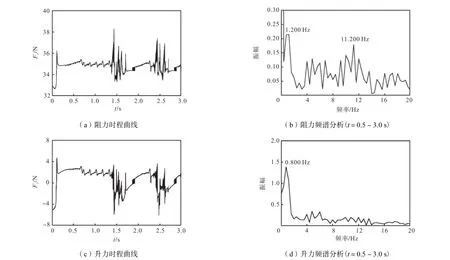
图14 U0=7.40m/s 时的拉索气动力Fig.14 Aerodynamic force of cable whenU0=7.40m/s

图15 U0=7.72ms时的水膜形态时程变化Fig.15Temporal evolution of water film morphology whenU0=7.72ms

2.3.3 U0=7.72m/s时

当风速增大到U0=7.72 ms 时，斜拉索表面水线的出现时间进一步提前，水膜形态变化也比U0=7.40 ms 时剧烈，如图15所示．下水线在t=0.09 s时形成于θ≈277.4°处，至t=0.66 s一直保持稳定，高度约为1.0 mm，宽度约为5.3 mm；在t=0.66 s后下水线开始出现振荡，其振荡区间大致位于θ=265.0°～285.9°，最大高度仍为1.0 mm，宽度变化范围为b=3.0～8.3 mm ．气流产生的风压力和风摩擦力使得水膜在迎风侧逐渐积聚，但由于重力的存在，这部分水膜并未形成上水线，而是沿迎风侧不断向下滑落，直到t=0.45 s 左右才出现了明显的上水线(θ≈57.7°)，高度约为1.0 mm，宽度约为4.0 mm；在t=0.49 s时又出现了第2条上水线(θ≈72.0°)，高度约为1.0 mm，宽度约为3.6 mm．上水线的形态要比下水线复杂得多，出现了1条上水线、2条上水线和3条上水线交替形成的现象，其振荡区间大致位于θ=44.1°～80.2°．当存在2条以上的上水线或上水线宽度较大时，受重力影响，上水线不断地从迎风侧分离出一部分水线向下滑落并与下水线汇合；而当只有1条较窄的上水线存在时就不出现上述现象．

以θ=0°处的水膜为研究对象，可以清楚地看出其厚度随着水线的不断滑落而发生变化，如图16(a)所示．从图16(b)所示的频谱分析图中可以发现其振荡频率f≈1.15Hz，与试验中拉索的自振频率f0≈0.952Hz比较接近．

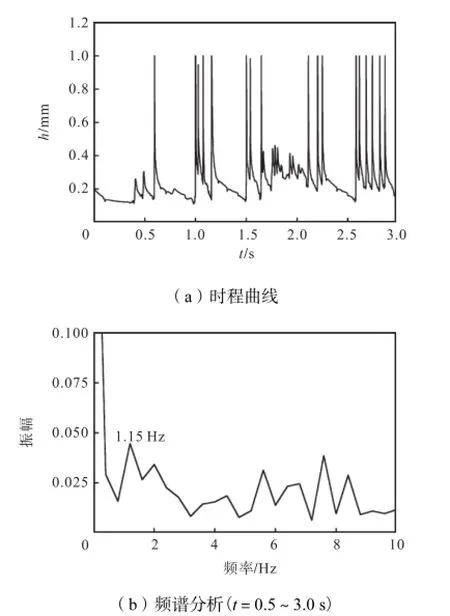
图16 U0=7.72m/s 时θ=0°位置处的水膜厚度Fig.16 Water-film thickness at the position of θ=0° when U0=7.72m/s

图17 所示的U0=7.72m/`s 时的拉索气动力变化与U0=7.40m/s时相似，但其幅值要大于U0=7.40m/s工况．对t=0.5～3.0s内的阻力和升力时程变化曲线进行频谱分析，可以得到阻力和升力的振荡频率分别为fx≈1.99Hz 和fy≈1.18Hz ，亦与文献[14]应用子结构法得到的结果相近．与U0=7.40m/s时相同，升力的振荡频率和θ=0°处的水膜厚度振荡频率均与拉索的自振频率相近，而U0=7.72m/s 同样位于风洞试验中发生风雨激振现象的显著风速范围内[7-8]，进一步说明水线形态的周期性变化引起拉索气动力的周期性变化，进而导致拉索发生共振，产生风雨激振现象．

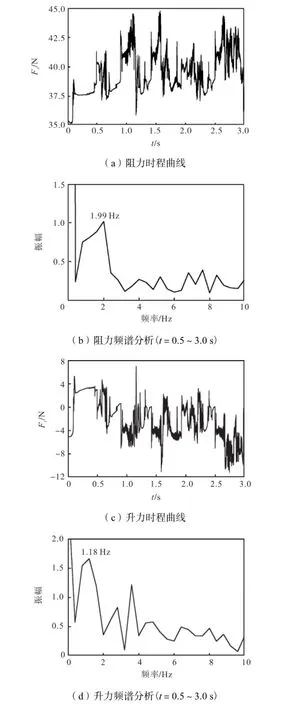
图17 U0=7.72ms时的拉索气动力Fig.17 Aerodynamic force of cable when U0=7.72m/s

2.3.4 U0=9.00m/s 时

随着风速的进一步加大，斜拉索表面水线的出现时间也越来越早，如图18所示．当U0=9.00m/s 时，下水线在t=0.07s 时形成于θ≈280.3°处，其振荡区间大致位于θ=267.3°～287.6°，最大高度为1.0,mm，宽度变化范围为b=3.2～8.5mm ．上水线的形成时间则提前到t=0.15s ，中心位置为θ≈63.5°，然后快速向背风侧移动，至t=0.17s 稳定在θ≈66.4°附近，高度约为1.0,mm，宽度约为3.5,mm；在t=0.19s 时又出现了第2条上水线，中心位置为θ≈52.6°，高度约为1.0,mm，宽度约为3.6,mm，而后一直保持稳定形态．从t=0.22s 开始，不断有水线在θ≈42.4°附近形成并从迎风侧沿拉索表面滑落至下水线并与下水线汇合，t=0.80s 前水线高度为1.0,mm，t=0.80s后水线高度逐渐减小至0.3,mm左右．

图18 U0=9.00m/s 时的水膜形态时程变化Fig.18 Temporal evolution of water film morphology when U0=9.00m/s

对应于拉索表面的某一固定位置则表现为水膜厚度的振荡，如图19所示．对t=0.5～3.0s 内θ=0°处的水膜厚度时程变化曲线进行频谱分析，发现其振荡频率f≈14.5Hz ，远远大于拉索的自振频率．

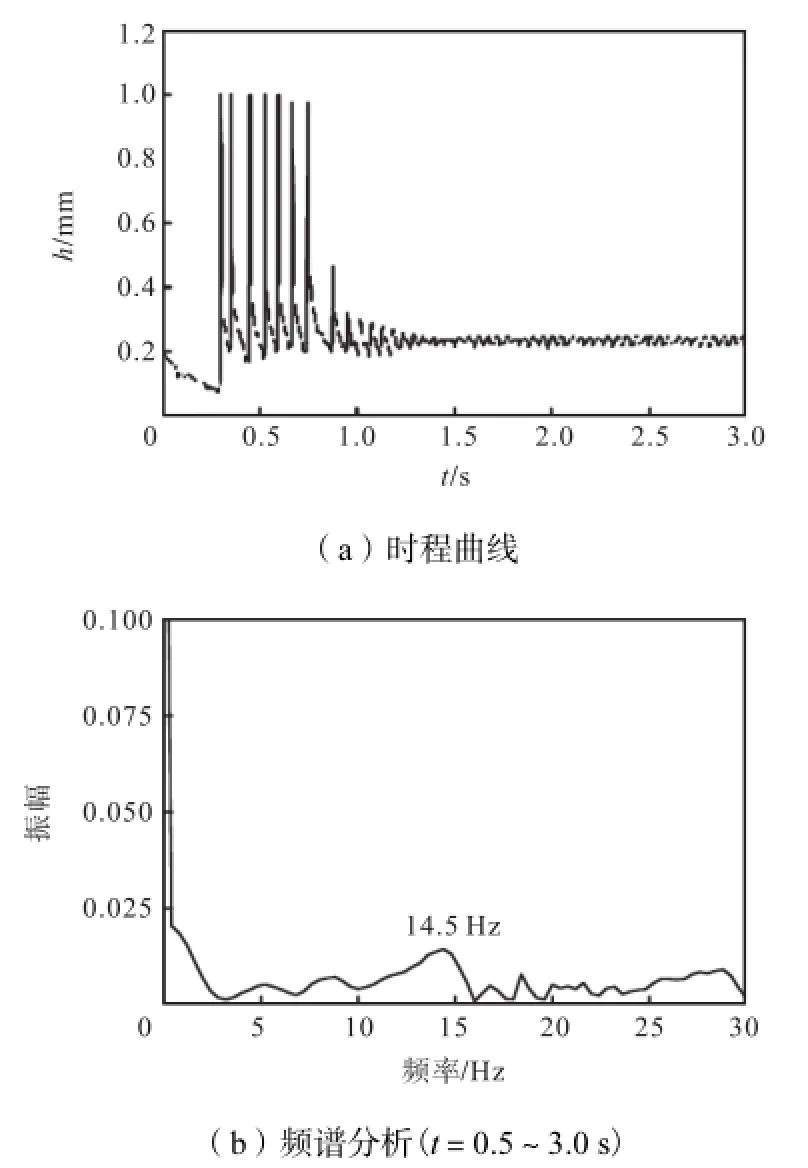
图19 U0=9.00ms时θ=0°位置处的水膜厚度Fig.19 Water-film thickness at the position of θ=0° when U0=9.00m/s

与U0=7.40m/s 和U0=7.72m/s时的情况类似，上水线形成前的拉索气动力变化仍与U0=6.00m/s时相似，随后上水线的形成和不断有水线向下滑落并与下水线汇合使得拉索气动力发生剧烈变化，风速的增大使得变化幅值也进一步增大，如图20(a)所示．通过对t=0.5～3.0s 内的阻力、升力时程变化曲线进行频谱分析，发现阻力和升力的频率基本相同(fx≈fy≈21.2Hz)，如图20(b)所示，但远大于拉索的自振频率．由于试验中U0=9.00m/s 时拉索不会发生风雨激振现象[7-8]，这也从侧面说明风雨激振现象的产生原因是水线与拉索的共振．

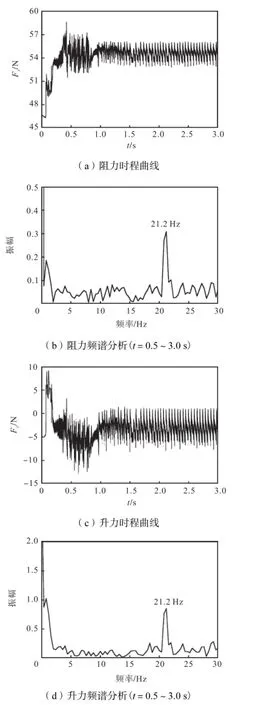
图20 U0=9.00m/s 时的拉索气动力Fig.20 Aerodynamic force of cable when U0=9.00m/s

3 结 论

本文应用滑移理论，从水膜运动方程出发，推导出斜拉索气动力计算公式，并且在数值计算中将滑移理论与计算流体力学相结合，应用Fluent软件获取每一时刻水膜表面的风压力系数Cp和风摩擦力系数Cf，建立了一个模拟风雨条件下斜拉索表面水膜形态变化的理论模型，考虑拉索倾斜角和风偏角，分析不同风速下斜拉索表面的水膜形态及拉索气动力的变化规律，得到以下结论．

(1) 风压力系数Cp和风摩擦力系数Cf在水线附近会发生显著变化．

(2) 水膜在重力、表面张力、气流产生的风压力和风摩擦力的作用下形成水线，但只有当风速大到一定程度时才会形成上水线；且上水线出现的时间要晚于下水线，形成上、下水线所需的时间随风速的增大而减少．

(3) 水膜形态的各种变化都会引起斜拉索升力的改变．当风速较小时，水膜形态稳定，斜拉索升力变化很小；当风速较大时，会从上水线分离出一部分水线与下水线汇合，导致斜拉索受力发生振荡，且振幅随风速的增大而增大．

(4) 与已有的试验结论[7]相一致，当气流方向与斜拉索下倾方向相同，且风速位于某一特定区域内时，水膜形态变化及其引起的拉索气动力变化均具有明显的周期性，二者频率基本相同，且接近拉索的自振频率；而当风速超过斜拉索发生风雨激振的最大风速时，拉索气动力频率远大于自振频率，说明风雨激振现象的产生是由于水线形态的周期性变化导致拉索气动力的周期性变化，进而导致拉索发生共振．

［1］ Bosdogianni A，Olivari D. Wind-and-rain-induced oscillations of cables of stayed bridges [J]. Journal of Wind Engineering and Industrial Aerodynamics，1996，64(2/3)：171-185.

［2］ Hikami Y，Shiraishi N. Rain-wind induced vibrations of cables stayed bridges [J]. Journal of Wind Engineering and Industrial Aerodynamics，1988，29(1/2/3)：409-418.

［3］ Ni Y Q，Wang X Y，Chen Z Q，et al. Field observations of rain wind induced cable vibration in cable stayed Dongting Lake Bridge [J]. Journal of Wind Engineering and Industrial Aerodynamics，2007，95(5)：303-328.

［4］ Zuo D，Jones N P，Main J A. Field observation of vortex and rain wind induced stay-cable vibrations in a three-dimensional environment [J]. Journal of Wind Engineering and Industrial Aerodynamics，2008，96(6/7)：1124-1133.

［5］ Gu M，Du X Q. Experimental investigation of rainwind-induced vibration of cables in cable-stayed bridges and its mitigation [J]. Journal of Wind Engineering and Industrial Aerodynamics，2005，93(1)：79-95.

［6］ Gu M. On wind-rain induced vibration of cables of cablestayed bridges based on quasi-steady assumption [J]. Journal of Wind Engineering and Industrial Aerodynamics，2009，97(7/8)：381-391.

［7］ Li F C，Chen W L，Li H，et al. An ultrasonic transmission thickness measurement system for study of water rivulets characteristics of stay cables suffering from wind-rain-induced vibration [J]. Sensors and Actuators A：Physical，2010，159(1)：12-23.

［8］ 许林汕，赵 林，葛耀君. 发生风雨激振拉索表面水膜形态数值分析和实测初探[J]. 空气动力学学报，2011，29(1)：91-96. Xu Linshan，Zhao Lin，Ge Yaojun. Numerical analysis and real-time measurement of water-film on rain-wind induced vibration cable [J]. Acta Aerodynamica Sinica，2011，29(1)：91-96(in Chinese).

［9］ Yamaguchi H. Analytical study on growth mechanism of rain vibration of cable [J]. Journal of Wind Engineering and Industrial Aerodynamics，1990，33(1/2)：73-80.

［10］ Gu M，Liu C J，Xu Y L，et al. Response characteristics of wind excited cables with artificial rivulet [J]. Applied Mathematics and Mechanics，2002，23(10)：1176-1187.

［11］ Xu Y L，Wang L Y. Analytical study of wind-rain induced cable vibration：SDOF mode [J]. Journal of Wind Engineering and Industrial Aerodynamics，2003，91(1/2)：27-40.

［12］ 毕继红，王青太，尹元彪. 拉索风雨激振机理及减振措施的研究[J]. 工程力学，2010，27(12)：229-237. Bi Jihong，Wang Qingtai，Yin Yuanbiao. The analysis of the mechanism of rain-wind-induced vibration and displacement-restriction device [J]. Engineering Me-chanics，2010，27(12)：229-237(in Chinese).

［13］ 李伟义，张琪昌，何学军. 斜拉索风雨激振面内运动的非线性分析[J]. 天津大学学报，2010，43(2)：156-160. Li Weiyi，Zhang Qichang，He Xuejun. Nonlinear analysis of in-plane motion of rain-wind-induced vibration of stay cable [J]. Journal of Tianjin University，2010，43(2)：156-160(in Chinese).

［14］ Lemaitre C，Hémon C，Langre E. Thin water film around a cable subject to wind [J]. Journal of Wind Engineering and Industrial Aerodynamics，2007，95(9/10/11)：1259-1271.

［15］ Li H，Chen W L，Xu F. A numerical and experimental hybrid approach for the investigation of aerodynamic forces on stay cables suffering from rain-wind induced vibration [J]. Journal of Fluids and Structures，2010，26(7/8)：1195-1215.

［16］ Achenbach E. Distribution of local pressure and skin friction around a circular cylinder in a cross-flow up to Re=5×10-6[J]. Journal of Fluid Mechanics，1968，34(4)：625-639.

［17］ 顾 明，杜晓庆. 带人工雨线的斜拉桥拉索模型测压试验研究[J]. 空气动力学学报，2005，23(4)：419-424. Gu Ming，Du Xiaoqing. Testing study on wind pressure distributions of stayed cables with an artificial rivulet [J]. Acta Aerodynamica Sinica，2005，23(4)：419-424 (in Chinese).

［18］ 李寿英，顾 明. 带固定人工水线拉索绕流的数值模拟[J]. 同济大学学报：自然科学版，2004，32(10)：1334-1338. Li Shouying，Gu Ming. Numerical simulation of flow around stayed cable with artificial rivulet [J]. Journal of Tongji University：Natural Science，2004，32(10)：1334-1338(in Chinese).

［19］ Fage A，Falkner V M. Further Experiments on the Flow Around a Circular Cylinder [M]. London：HM Stationery Office，1931.

［20］ Celika I，Shaffer F D. Long time-averaged solutions of turbulent flow past a circular cylinder [J]. Journal of Wind Engineering and Industrial Aerodynamics，1995，56(2/3)：185-212.

［21］ 陈政清，项海帆. 桥梁风工程[M]. 北京：人民交通出版社，2005. Chen Zhengqing，Xiang Haifan. Wind Engineering of Bridge[M]. Beijing：China Communications Press，2005(in Chinese).

(责任编辑：樊素英)

Variation of Water Film Morphology and Aerodynamic Force of Stay Cable

Bi Jihong1,2，Wang Jian1，Lu Peng1，Bao Chun1
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin 300072，China)

The formation and oscillation of rivulets around stay cable play an important role in rain-wind induced vibration(RWIV). To study the influence of rivulet motion on the RWIV of stay cable，with lubrication theory and computational fluid dynamics method combined，a theoretical model for simulating the morphological change of water film around stay cable under wind and rain is presented，and a formula for the aerodynamic force of stay cable is derived from water-film motion equation. The variations of water film morphology and aerodynamic forceof stay cable are obtained by numerical simulation，and the internal relationships between them are analysed. Compared with the existing experimental results，it can be found that when RWIV of stay cable occurs，the change frequenciesof rivulet morphology and aerodynamic force are close to the natural frequency of stay cable，which indicates thatthe cause of RWIV is the resonance of cable induced by the periodic change of rivulet morphology.

rain-wind induced vibration(RWIV)；stay cable；rivulet；water film；aerodynamic force；lubrication theory

U443.38

A

0493-2137(2014)06-0479-12

10.11784/tdxbz201208050

2012-08-29；

2013-04-23.

国家自然科学基金资助项目(61002027).

毕继红（1965— ），女，教授，博导．

毕继红，jhbi@sohu.com．

时间：2014-03-18.

http://www.cnki.net/kcms/doi/10.11784/tdxbz201208050.html.