高超声速飞行器自适应高阶终端滑模控制

宗 群，苏 芮，王 婕，田栢苓

(天津大学电气与自动化工程学院，天津 300072)

高超声速飞行器自适应高阶终端滑模控制

宗 群，苏 芮，王 婕，田栢苓

(天津大学电气与自动化工程学院，天津 300072)

针对高超声速飞行器的纵向运动模型，研究了飞行器输出跟踪控制问题，提出了一种将动态逆方法与高阶终端滑模控制相结合的鲁棒自适应控制方法. 首先，利用反馈线性化方法对高超声速飞行器纵向模型输入输出线性化；通过设计具有全局鲁棒性的终端滑模面，提高系统的输出收敛速度；同时，采用自适应高阶滑模控制律，在不确定上界未知条件下对其进行自适应估计，从而实现控制器增益的实时在线调整，减少系统抖振；最后，基于Lyapunov理论证明了此控制策略可以保证闭环系统稳定. 仿真结果表明，所设计的控制器能够实现高超声速飞行器纵向爬升机动中速度和高度的稳定跟踪控制.

鲁棒自适应控制；飞行控制；高阶滑模；终端滑模

高超声速飞行器飞行环境复杂、飞行包线跨度大、动态特性易变且采用机体/发动机一体化设计技术，导致气动参数与发动机推力之间存在强烈耦合．这些特点对飞行控制系统研究设计提出了许多新的挑战，使高超声速飞行控制成为当前飞行器控制研究领域的前沿问题．

目前在控制领域中受到广泛采用和认可的模型是美国空军实验室学者Bolender和Doman[1]研究的一体化解析式模型，该模型全面地刻画了吸气式高超声速飞行器的纵向动力学行为．在此基础上Parker等[2]考虑高超声速飞行器的气推耦合和弹性振动，建立了曲线拟合模型，利用线性二次型调节器(LQR)理论设计了一种多输入多输出的最优控制器；随后，文献[3]提出增加鸭翼变量，消除控制舵面对升力的气动耦合项所导致的非最小相位行为，设计了基于反馈线性化方法的LQR控制器．Rehman等[4]针对反馈线性化方法应用中存在的输入耦合和模型不确定性问题，提出了一种由鲁棒反馈线性化和最小最大LQR相结合的控制方法，但该方法无法满足飞行器控制的实时性．

为了获得更好的控制性能，一些学者提出Terminal滑模控制策略[5]，确保滑模面上的跟踪误差在有限时间内收敛到零．进一步，文献[6]提出了适用于高阶非线性系统的Terminal滑模面，克服了滑模面函数导数不连续的缺点，消除了滑模控制的到达阶段，保证了系统的全局鲁棒性．虽然Terminal滑模控制可以使系统状态在有限时间内收敛，提高收敛速度和跟踪精度，但是仍然没有克服抖振问题．近年提出的高阶滑模控制方法将高频切换控制转移到滑模变量的高阶导数上，有效消除了抖振，同时保留着传统滑模的良好特性[7-8]．此外，Su等[9]采用自适应律对有界不确定性进行估计，提出了自适应滑模控制，并应用于机械臂的跟踪控制．

为了针对高超声速飞行器直接设计高性能的自适应鲁棒非线性控制器，本文将高次幂多项式型非奇异终端滑模与高阶滑模控制方法相结合，用于消除抖振并提高系统控制性能．针对飞行器输入输出线性化模型设计非奇异终端滑模面，同时利用自适应方法估计有界的不确定上界，进一步利用自适应高阶滑模控制策略，实时在线调整控制增益，使系统的状态收敛至平衡点，消除控制抖振，对高超声速飞行器速度与高度的阶跃参考信号实现稳定跟踪.

1 模型描述

1.1 吸气式高超声速飞行器模型

本文考虑的吸气式高超声速飞行器纵向动力学模型来源于文献[1]的研究成果．基于平面地球假设，将飞行器建模为一个弹性结构，推导的运动方程中包含弹性效应，同时刚体动力学和弹性动力学之间通过气动力产生耦合．运动方程表达式为

式中：v为速度；h为高度；γ为航迹角；α为攻角；Q为俯仰角速率；它们为系统的5个刚体状态；iη和 η˙i(i=1,2,3)为系统的6个弹性状态．选择速度v和高度h为系统输出量，控制输入为油门开度φ、升降舵偏转量δe、鸭翼偏转量δc和扩散面积比Ad．控制输入通过气动力(升力L和阻力D)、俯仰力矩M、广义力Ni和发动机推力T影响飞行器动态．在标准质量下，弹性结构的阻尼和自然频率分别为ςm,i和ωm,i．其他变量此处不再说明，其具体含义可参见文献[3，10]．

将前体转角τ1和后体转角τ2的变化量分别记为Δτ1和Δτ2，广义坐标与Δτ1、Δτ2满足线性映射关系，该线性映射与飞行器质量m相关．俯仰力矩M、气动力(升力L和阻力D)、广义力Ni及发动机推力T的表达式分别为

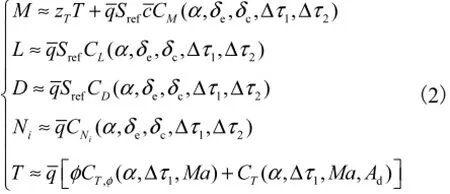
式中：CM为俯仰力矩系数；CL和CD分别为气动力升力系数和阻力系数；CNi为广义力系数；CT,φ和CT为推力系数．这些系数的计算式分别为

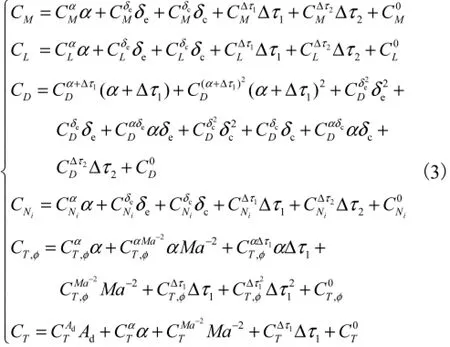
此外，动压q和自由流马赫数Ma的表达式为

式中：c为声速；k0为比热系数，k0=1.4；R为气体常数，R=286.9,J/(kg·K)；T∞(h)为自由流温度；ρ(h)为与高度相关的空气密度．T∞(h)和ρ(h)由1976年美国标准大气中以高度为参数查询获得．文中选取的物理参数如下所示：参考面积Sref=1.579,m2，平均气动弦长c=5.181,6,m，惯性力矩Iyy=677,909,kg/m，弹性结构的阻尼为ςm,i=0.02，重力加速度g= 9.81,m/s，自然频率为ωm,1=21.17,rad/s，ωm,2= 53.92,rad/s，ωm,3=109.1,rad/s[11]．

1.2 高超声速飞行器模型输入输出线性化

针对高超声速飞行器模型(1)进行输入输出线性化．首先，忽略弹性状态ηi和η˙i的影响，并将鸭翼偏转量δc设为舵偏转量δe的函数，具体表达式为

式中kec为比例系数，k=-()，这样即可消除

ec控制舵面对升力的气动耦合项所导致的非最小相位行为[4]．在此基础上，进一步忽略力和力矩系数式(3)中控制舵面对升力、阻力系数的耦合项以及弹性模态引起的不确定性，将式(3)简化为

简化后的模型只含有5个刚体状态，即系统阶数为5．考虑到动态逆条件[12]，即系统的阶数与系统的相对阶相等，引入二阶执行器动态使系统阶数升为7，其具体形式为

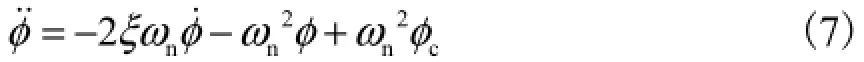
式中φc为燃油当量比．

经过上述对模型的简化与处理，下面将给出系统相对阶的计算过程．

假设在实际飞行过程中油门全开，即扩散面积比Ad=1，对系统输出y=[vh]Τ分别求3次与4次导数，直至出现控制输入u =[φcδe]Τ，得到

其中vf、hf、11b、12b、21b、22b的具体表达式分别为

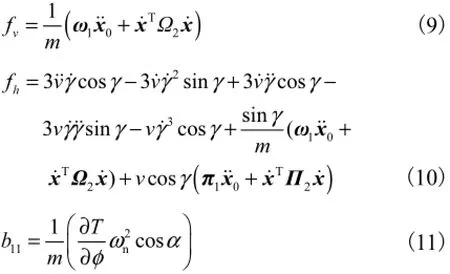
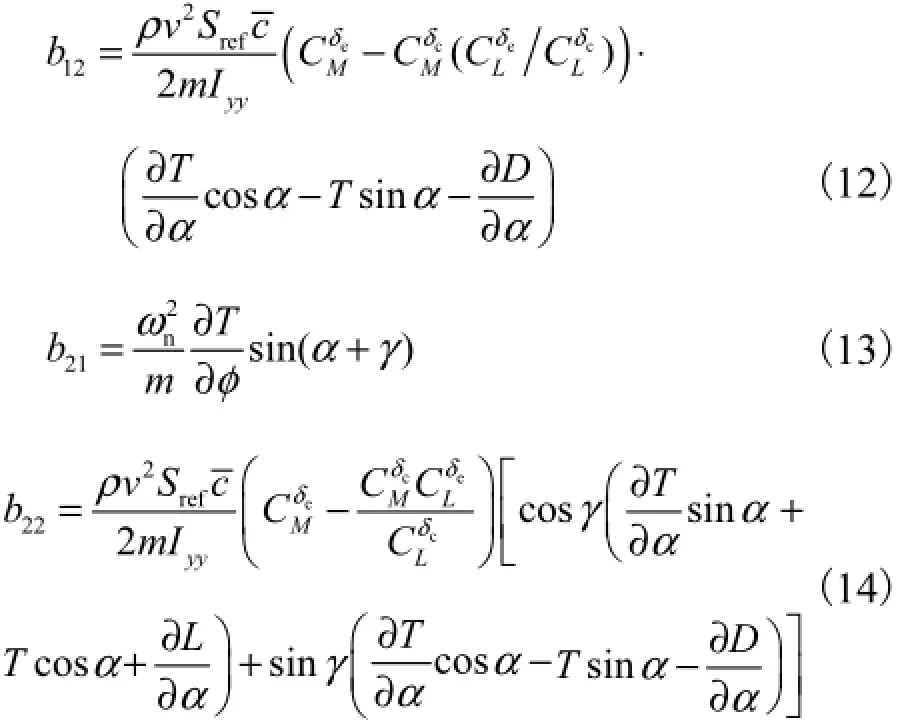
由式(8)可知，对速度v和高度h分别微分3次和4次，控制输入u =[φcδe]Τ出现在最后的微分式子中，则系统的相对阶为7，与系统的阶数相等，满足动态逆条件，系统的零动态是稳定的，因此高超声速飞行器纵向模型可以实现输入输出线性化．令，考虑弹性飞行器模型的不确定性，相应地方程(8)可写为积分链形式，即

2 自适应高阶终端滑模控制器设计

本文讨论的高超声速飞行器跟踪控制问题是针对弹性飞行器模型(1)存在不确定的情形下，设计高阶终端滑模控制器，使得速度v和高度h实现对期望速度dv和期望高度dh的稳定跟踪．

2.1 终端滑模面设计

定义飞行速度与高度的跟踪误差分别为

基于跟踪误差，分别设计速度滑模面vS与高度滑模面hS[12]为

式中：cv和ch为正系数向量，cv=[c11,c12,c13]，ch=

分析可知，式(19)与式(20)及后续稳定性证明过程中需要用到ve以及he的高阶导数，而其高阶导数无法直接测量．本文利用具有鲁棒性强、精度高、收敛快等优点的高阶滑模微分器[14]，获取状态ve与he的微分估计值．由于篇幅所限，这里只给出ve的高阶滑模微分器的表达式为

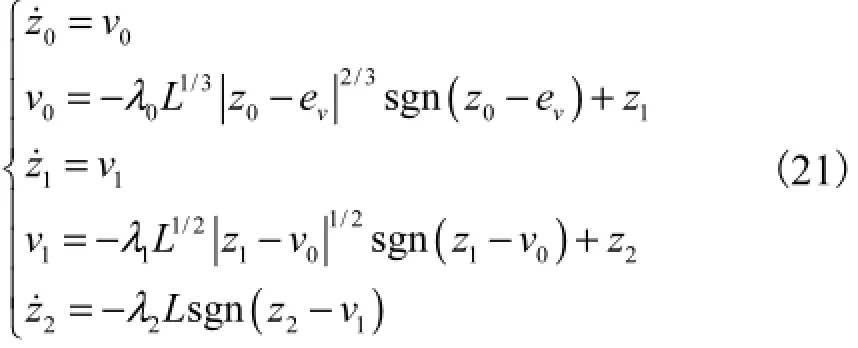
式中：ev为待微分信号；vi(i=0,1)为ev的第i+1阶微分估计值；zk(k=1,2)为系统(21)中的内部状态；λ0,λ1,λ2为微分器的设计参数．

根据文献[6]的研究，Pv(t)=[pv(t),p˙v(t),˙p˙v(t)]Τ与Ph(t)=[ph(t),p˙h(t),˙p˙h(t),˙p˙˙h(t)]Τ满足下列假设.

假设1：P(t)∈C3[0,∞)，P(t)∈C4[0,∞)且

vh当t≥t时P(t)和P(t)恒为零

0

vh (i=1,2,3;j =1,2,3,4)．

设计Pv(t)和Ph(t )的表达式分别为

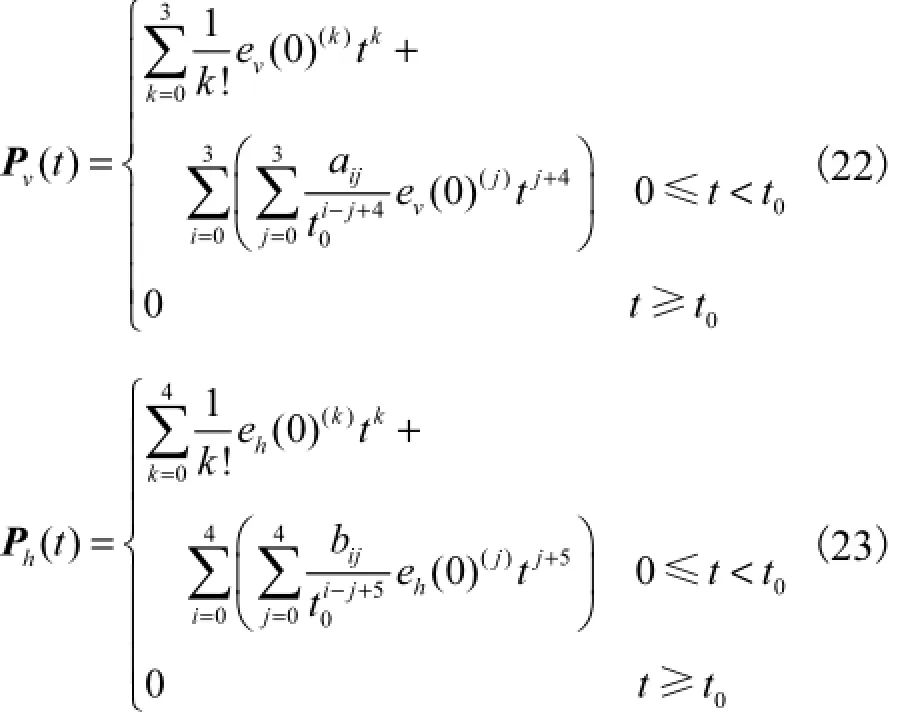
根据假设1，Pv(t)和Ph(t)应为连续光滑函数，因而当t=t0时，Pv(t)和Ph(t)及其导数为零．相应地，可求出系数aij(i=1,2,3;j =1,2,3)与bij(i=1,…,4; j=1,…,4)的具体值，具体求解过程可参考文献[6]．

假设2：假设Δ1和Δ2是有界的，即max{Δ1,Δ2}≤M0，其中M0为不确定上界．

2.2 终端滑模控制器设计

通过式(19)和式(20)可知，系统的初始状态在滑模面上，消除了滑模到达过程，控制器设计具有全局鲁棒性．

定理1：针对非线性不确定系统式(15)和式(16)，若假设1与假设2成立，则控制律

能够确保Sv、Sh及误差变量Ev与Eh快速收敛到零，其中B=[b1,b2]Τ、b1=[b11b12]、b2=[b21b22]，切换增益系数K满足K≥max{c13M0,c24M0}．

证明：记S =[SvSh]Τ，取Lyapunov函数为

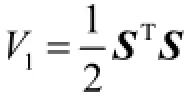
由式(19)和式(20)可知，分别对速度滑模变量Sv与高度滑模变量Sh求一阶导数可出现控制量u，即

令μ1=K-c13M0，μ2=K-c24M0，则μ1和μ2均为非负值．对求取一阶导数，并将定理1中控制律u代入，得到

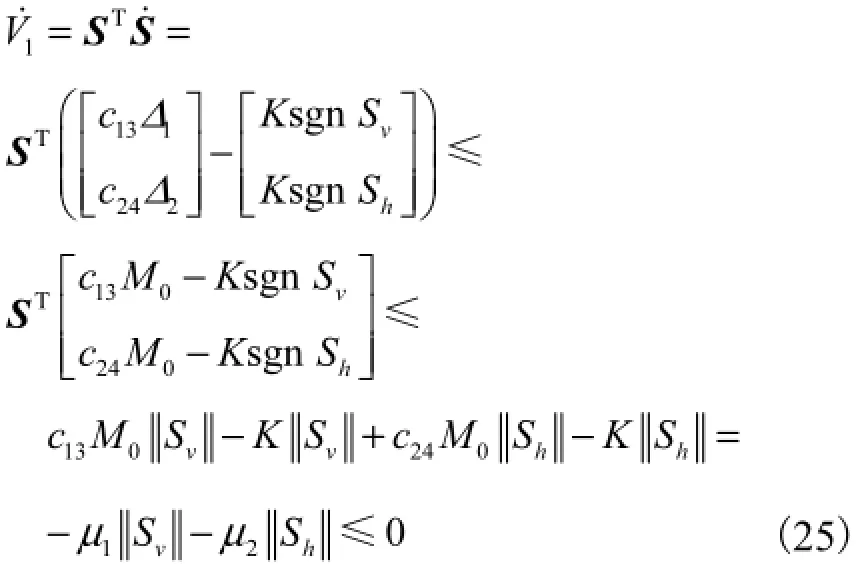
设计上述的高阶滑模控制律需要知道不确定的上界，即要求M0的值已知，但实际应用中很难预先获得M0的确定值．因此，为满足滑模面函数S=0的可达性，控制器的增益往往取得过大，带有很大的保守性，容易导致抖振．下文将提出一种自适应控制律的设计方法，控制增益能够根据系统状态自动调节，不需事先知道系统不确定的上界．

根据式(25)设计控制律

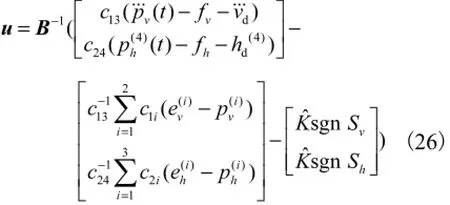
式中ˆK为自适应增益系数．

根据式(25)将集中的不确定记为

假设存在正数Kd为系统稳定后Kˆ的最终值，则Kd必须满足Kd＞Δ．设计自适应律为

式中：μ为自适应调整参数，μ＞0；Kˆ自动调节的速率取决于μ的大小．下面将通过Lyapunov方法证明控制律(26)的有效性．令σ=Kd-Δ，则α＞0．此外，令K˜=Kˆ-Kd．

选取Lyapunov函数为

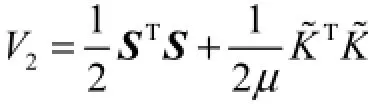
对其求取一阶导数为

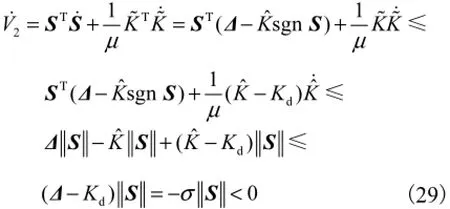
证毕．

3 仿真分析

将上述控制器(26)在Matlab/Simulink环境中进行仿真以验证其有效性．针对飞行器纵向爬升机动过程，分别考虑飞行速度阶跃变化量vΔ=30.5,m/s及飞行高度阶跃变化量hΔ=610,m.其中，飞行器的初值设置及两种测试情形下的稳态值见表1．

表1 飞行器初始状态及两种情形下的稳态值Tab.1 Initial condition of the flight vehicle and steady-state values for two different cases

选取自适应调整参数μ=0.2，滑模面增益设为cv=[662]与ch=[6664]．跟踪速度阶跃参考信号时，飞行器的状态(速度和高度)变化情况见图1，控制输入燃油当量比cφ与升降舵偏转量eδ的变化见图2，自适应增益ˆK的变化如图3所示．同理，跟踪高度阶跃参考信号时，飞行器的状态、控制输入及自适应增益ˆK的变化如图4～图6所示．

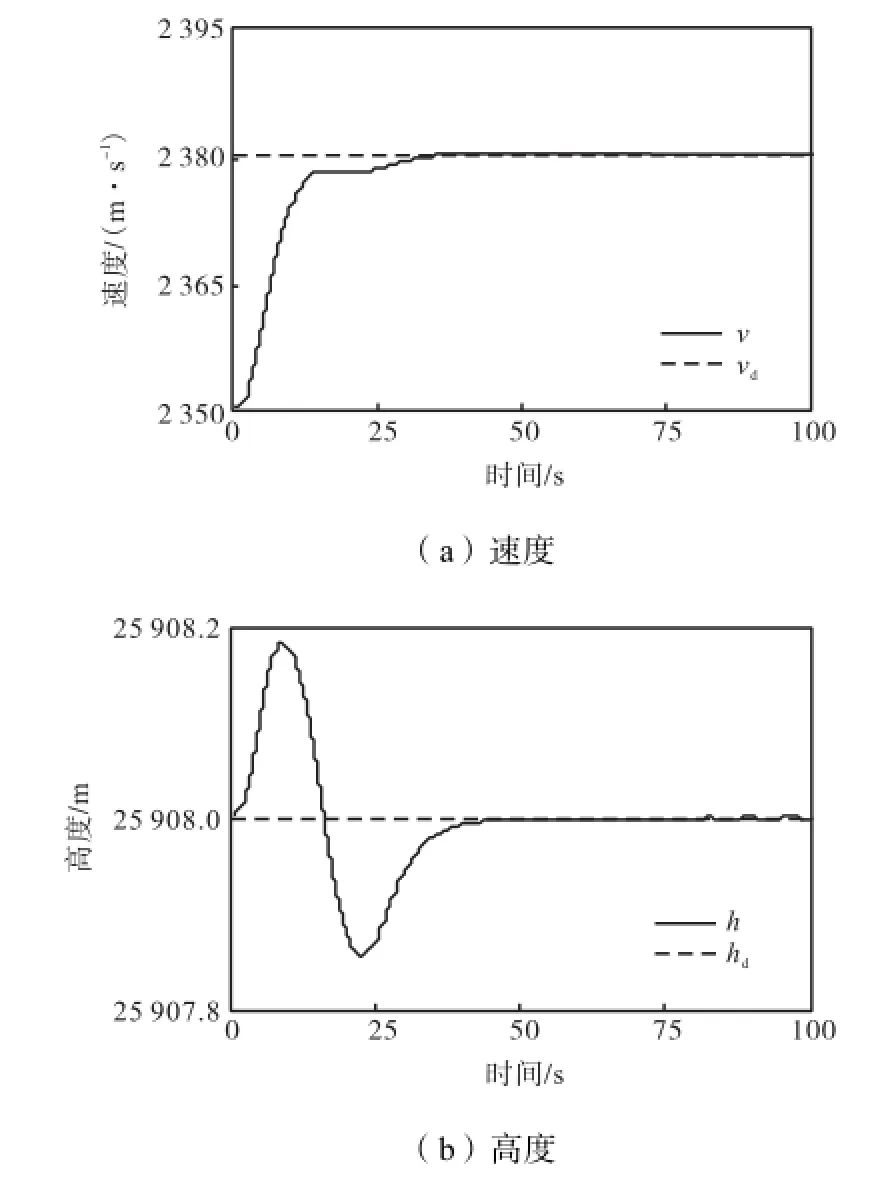
图1 飞行器状态变化情况(跟踪30.5,m/s速度阶跃指令)Fig.1 Change of vehicle state(tracking a 30.5,m/s stepvelocity command)

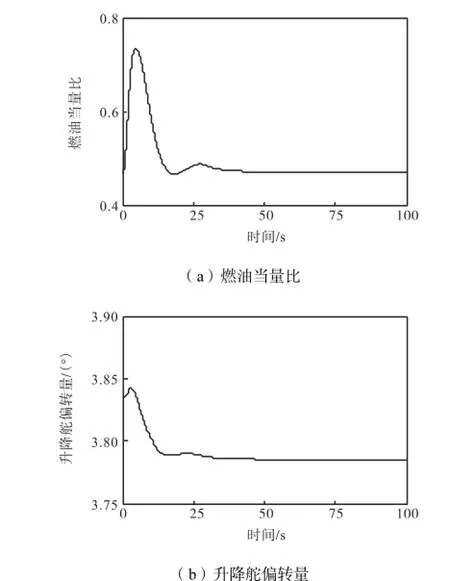
图2 控制量变化情况(跟踪30.5,m/s速度阶跃指令)Fig.2 Change of the control inputs(tracking a 30.5,m/s step-velocity command)

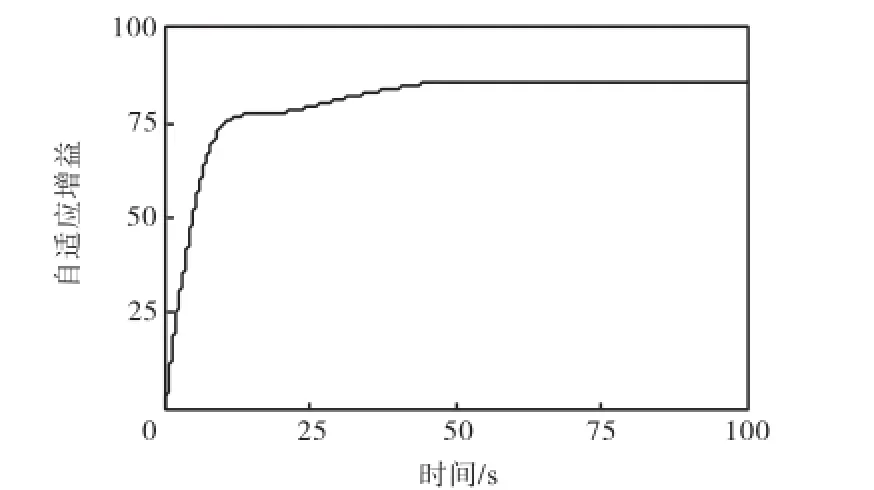
图3 跟踪速度阶跃指令(30.5,m/s)时的自适应增益ˆKFig.3 Adaptive gain parameter ˆK of tracking a 30.5,m/s step-velocity command

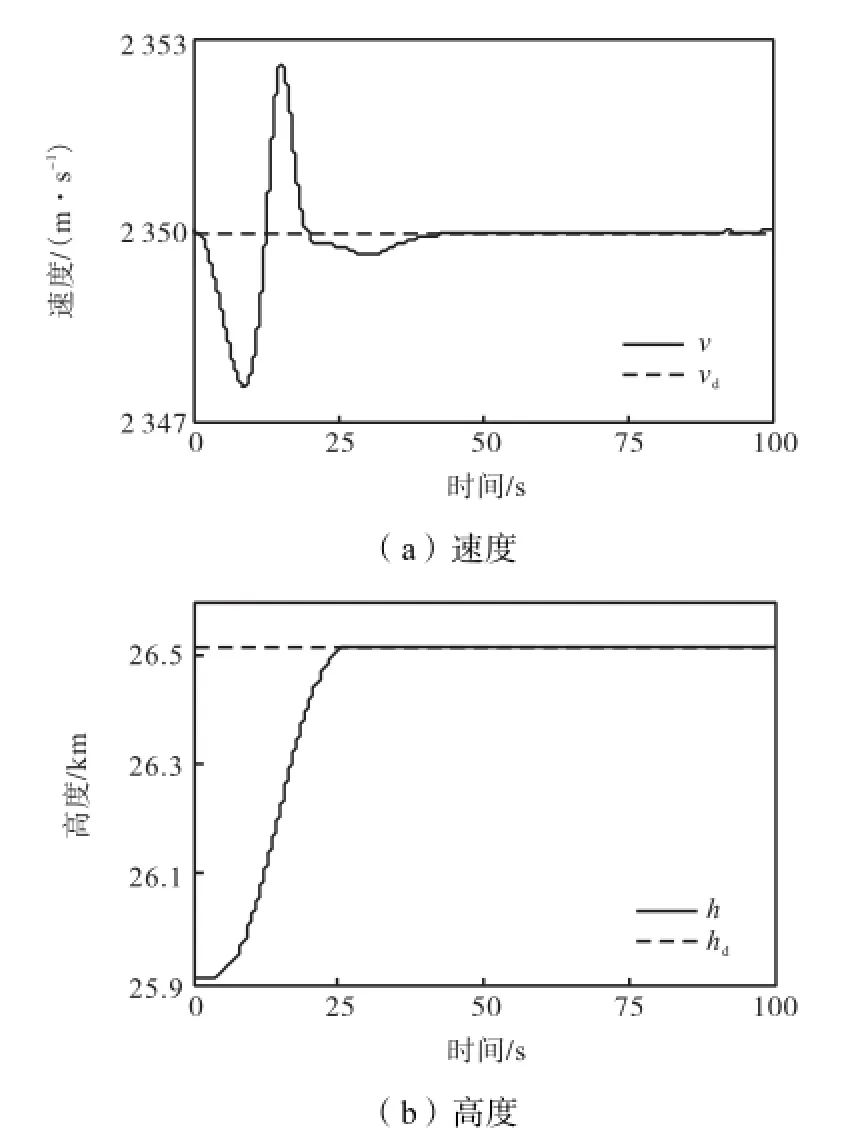
图4 飞行器状态变化情况(跟踪610,m高度阶跃指令)Fig.4 Change of the vehicle state(tracking a 610,m stepaltitude command)

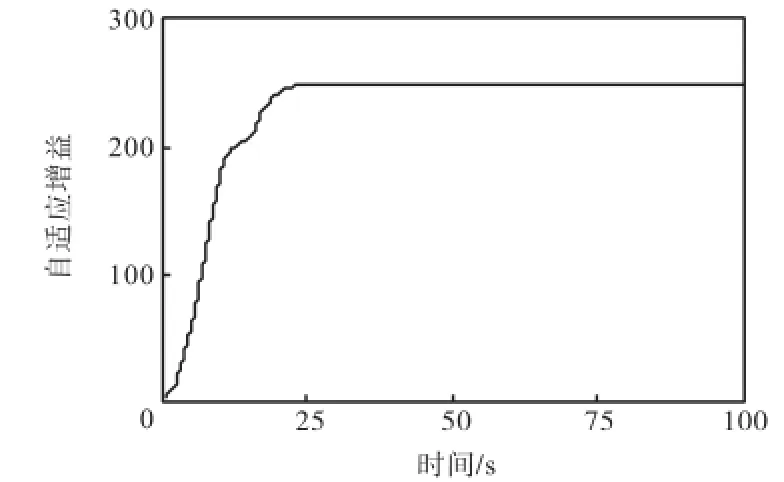
图5 跟踪610,m高度阶跃指令时的自适应增益ˆKFig.5 Adaptive gain parameter ˆK of tracking a 610,m step-altitude command

从仿真结果可以看出，自适应高阶终端滑模控制保证高超声速飞行器飞行速度和高度能快速跟踪上各自的参考指令值，并且没有稳态误差，控制输入cφ与eδ在飞行器进入稳定状态后都各自趋于稳态值．

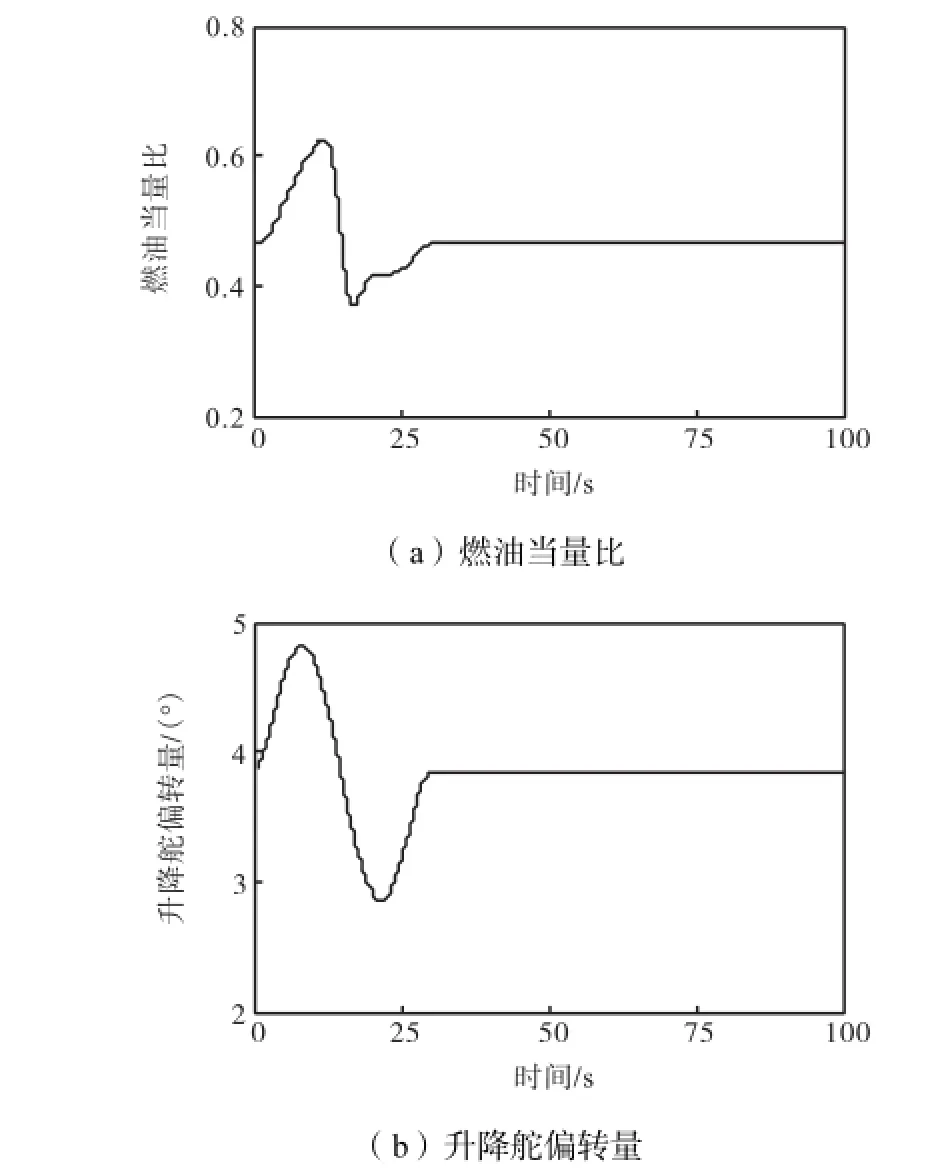
图6 控制量变化情况(跟踪610,m高度阶跃指令)Fig.6 Change of the control inputs(tracking a 610,m stepaltitude command)

4 结 语

本文针对高超声速飞行器纵向运动学模型具有高度非线性、多变量耦合、多不确定及易受弹性影响等特点，提出了一种基于非线性动态逆的自适应高阶终端滑模鲁棒控制器设计方法．采用非线性动态逆方法设计飞行器速度与高度跟踪的高阶终端滑模控制器，并采用自适应策略降低了系统对模型有界不确定的保守性．仿真结果表明，所提出的控制方法具有较好的跟踪性能与鲁棒性．

［1］ Bolender M A，Doman D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle [J]. Journal of Spacecraft and Rockets，2007，44(2)：374-387.

［2］ Parker J T，Serrani A，Yurkovich S，et al. Approximate feedback linearization of an air-breathing hypersonic vehicle[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit. Keystone，Colorado：American Institute of Aeronautics and Astronautics，2006：1-16.

［3］ Parker J T，Serrani A，Yurkovich S，et al. Controloriented modeling of an air-breathing hypersonic vehicle[J]. Journal of Guidance，Control and Dynamics，2007，30(3)：856-869.

［4］ Rehman O U，Fidan B，Petersen I. Uncertainty modeling and robust minimax LQR control of hypersonic flight vehicles[C]//AIAA Guidance，Navigation，and Control Conference. Toronto，Ontario，Canada：American Institute of Aeronautics and Astronautics，2010：1-15.

［5］ Wu Y Q，Yu X，Man Z H. Terminal sliding mode control design for uncertain dynamic system [J]. Systems and Control Letters，1998，34(2)：281-287.

［6］ Zhuang Kaiyu，Su Hongye，Zhang Keqin，et al. Adaptive terminal sliding mode control for high order nonlinear dynamic systems [J]. Journal of Zhejiang University Science，2003，4(1)：58-63.

［7］ Levant A. High order sliding modes，differentiation and output feedback control [J]. International Journal of Control，2003，76(9)：924-941.

［8］ Defoort M，Floquet T，Kokosy A，et al. A novel higher order sliding mode control scheme [J]. System & Control Letters，2009，58(2)：102-108.

［9］ Su C Y，Leung T P. A sliding mode controller with bound estimation for robot manipulators [J]. IEEE Transactions on Robotics and Automation，1993，9(2)：208-214.

［10］Wang Jie，Zong Qun，Tian Bailing，et al. Flight control for flexible hypersonic vehicle based on quasicontinuous high-order sliding mode[J]. Journal of Systems Engineering and Electronics，2013，24(2)：288-295.

［11］Sigthorsson D O，Serrani A. Development of linear parameter-varying models of hypersonic air-breathing vehicles[C]//AIAA Guidance，Navigation，and Control Conference. Chicago，Illinois：American Institute of Aeronautics and Astronautics，2009：1-21.

［12］Isidori A. Nonlinear Control Systems [M]. Berlin：Springer-Verlag，1995.

［13］Xu H J，Mirmirani M D，Ioannou P A. Adaptive sliding mode control design for hypersonic flight vehicle [J]. Journal of Guidance，Control，and Dynamics，2004，27(5)：829-838.

［14］Levant A. High-order sliding modes，differentiation and output-feedback control [J]. International Journal of Control，2003，76(9/10)：924-941.

(责任编辑：孙立华)

Adaptive High-Order Terminal Sliding Mode Control for Hypersonic Flight Vehicle

Zong Qun，Su Rui，Wang Jie，Tian Bailing
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

A robust control strategy combining adaptive high order terminal sliding mode with dynamic inversion was designed for the uncertain longitudinal dynamics of hypersonic vehicles about the output tracking problem. The feedback linearization method was adopted in this paper to linearize the input and output of a hypersonic vehicle longitudinal model. Then，the terminal sliding surface which possessed the global robustness was designed to improve the convergence rate of the output vector. Afterwards，the gain of the controller achieved real-time online adjustment by the adaptive high order sliding mode control strategy，through which the chattering was reduced. Finally，the finitetime stability of the closed-loop system was guaranteed based on the Lyapunov theory. Simulation results show that the designed controller is effective in climbing maneuvers of velocity and altitude reference commands respectively.

robust adaptive control；flight control；high-order sliding mode；terminal sliding mode

TP273

A

0493-2137(2014)11-1031-07

10.11784/tdxbz201309014

2013-09-03；修回日期：2013-11-01.

国家自然科学基金资助项目(61273092，61203012)；教育部科学技术研究重大资助项目(311012)；天津市自然科学基金资助项目(12JCZDJC30300)；中国航空科学基金资助项目(20125848004)；天津市过程检测与控制重点实验室开放基金资助项目(TKLPMC-201315)；天津大学自主创新基金资助项目(2013XQ-0022).

宗 群（1961— ），男，博士，教授．

宗 群，zongqun@tju.edu.cn

时间：2014-03-25.

http：//www.cnki.net/kcms/doi/10.11784/tdxbz201309014.html.