等弯曲强度条件下渐开线少齿数齿轮副的变位

孙月海，刘彦峰，段路茜，葛 楠

等弯曲强度条件下渐开线少齿数齿轮副的变位

孙月海1,2，刘彦峰1，段路茜3，葛 楠1

(1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 天津大学轻型动力教育部工程研究中心，天津 300072；3. 装甲兵工程学院机械工程系，北京 100072)

针对渐开线少齿数齿轮副强度较弱的问题，以平面渐开线少齿数齿轮副为研究对象，以增强小齿轮轮齿弯曲强度并使大小齿轮具有相同或接近的弯曲强度为设计条件，对渐开线少齿数齿轮副大小齿轮的径向变位系数和切向变位系数的选择进行了研究．通过对齿轮副轮齿最大弯曲应力的分析，推导出大小齿轮径向变位系数和切向变位系数应满足一定的函数关系．径向变位系数的选择需要考虑轮齿根切和齿轮副无侧隙啮合两方面因素，即小齿轮的径向变位系数应满足避免根切的条件，而齿轮副径向变位系数之和要满足一定函数关系．切向变位系数的选择需要考虑切向变位对大小齿轮啮合情况与弯曲强度的相互影响，小齿轮切向变位过大会使大齿轮的齿厚过小，削弱大齿轮的弯曲强度，同时有可能引起小齿轮齿根齿廓干涉．对于齿数、模数确定的少齿数齿轮副，以大小齿轮径向变位系数和切向变位系数应满足的各个函数条件为依据，通过建立变位系数的数学模型，可以获得轮齿副等弯曲强度条件下大小齿轮径向和切向变位系数的最佳组合．

齿轮；少齿数齿轮副；弯曲强度；变位系数

少齿数齿轮副一般是指小齿轮齿数小于8的齿轮副．近年来，少齿数齿轮副越来越多地被用于传动比大而空间位置有特殊要求的航空航天、精密仪器等传动装置中．但由于齿数少、齿轮端面尺寸小，使小齿轮的强度特别是轮齿弯曲强度较弱，造成少齿数齿轮副的承载能力较低，影响了该类齿轮副的广泛使用．

Ishibashi等[1]为了能使少齿数齿轮副具有较高的承载能力，对齿轮副的径向变位进行了研究．结果表明，过大的径向变位系数会引起少齿数齿轮轮齿变尖、齿高缩短，降低齿轮的重合度，影响齿轮副的承载能力．Ishibashi等[2]还研究了小齿轮齿数为3～5的渐开线齿轮与圆弧齿轮的承载能力对比情况. Chen等[3]利用齿轮的径向变位结合齿条型刀具齿廓修形的方法提出了无根切、高重合度、高强度的少齿数齿轮副的设计制造方法．Pan等[4]基于少齿数齿轮连续传动性差和根切等问题，对齿轮的径向变位系数和螺旋角的选择进行了研究，得到了较好的设计参数．蒋军[5]提出在径向变位的基础上引入切向变位，通过改变齿条刀具的齿厚来改变被切制齿轮的齿厚和齿高，对于提高齿轮副的承载能力具有较好的借鉴意义，但对于如何确定变位系数并未见诸报道．王树平[6]基于提高少齿数齿轮副的承载能力，进行了少齿数齿轮的齿形设计研究，提出了齿轮副廓形界限域的概念，为提高齿轮副的承载能力提供了新思路．赵向飞等[7]对少齿数齿轮的变位系数进行了研究，通过增大滚刀刀顶圆角半径的方法，使小齿轮齿顶厚和重合度都有所提升．孙伏等[8]对渐开线少齿数齿轮弯曲疲劳应力的计算系数进行了研究，通过设计相关实验，对齿数为4～11的齿轮进行了分析，得到了弯曲疲劳应力计算中齿形系数和应力修正系数变化曲线、齿顶变尖极限曲线和齿根根切极限曲线，对少齿数齿轮的弯曲强度计算具有一定的借鉴意义．

在齿轮传动中，齿轮副获得高承载能力的基础设计方法之一是使轮齿副具有相同或接近的弯曲强度．对于具有通常齿数的渐开线齿轮副设计，一般大小齿轮的轮齿形状较为接近，或相差并不悬殊．而少齿数(特别是齿数小于6)的齿轮齿形偏小，其弯曲强度较与之啮合的大齿轮轮齿差别较大．为此，本文以平面渐开线少齿数齿轮副为研究对象，以获得大小齿轮达到相等或接近的轮齿弯曲强度为设计条件，对少齿数齿轮副大小齿轮的径向变位系数和切向变位系数数值的选择计算进行了研究．

1 少齿数齿轮副等弯曲强度参数设计

在一些情况下，大小齿轮具有相同或接近的弯曲强度是齿轮副获得高强度设计的主要条件．本文主要研究齿轮副的两个轮齿具有相同弯曲强度的参数关系．

1.1 小齿轮的最大弯曲应力分析

小齿轮齿数小于6的齿轮副的端面啮合重合度一般小于1，小齿轮齿数为6、7、8时会出现重合度略大于1的情况．但考虑到制造和安装误差的影响，很有可能会出现单对齿承担所有载荷的情况，因此，本研究以单齿啮合为条件开展少齿数齿轮副的弯曲应力分析．图1所示为小齿轮齿顶A处和大齿轮啮合的情况，此时小齿轮齿根处产生的弯曲应力最大，是判断小齿轮最高弯曲强度的依据．将此时的弯曲应力作为小齿轮的计算弯曲应力．

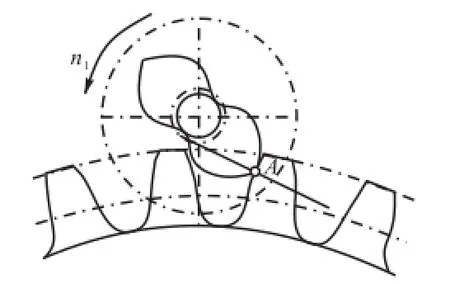
图1 小齿轮齿顶与大齿轮啮合Fig.1 Meshing of pinion and big gear

求解齿轮弯曲应力的基本公式[9]为

式中：Fσ为齿根危险截面所受的最大弯曲应力；M为齿根危险截面所受的最大弯矩；W为轮齿危险截面的抗弯截面系数．

按照轮齿等效悬臂梁的材料力学分析模型，小齿轮齿根危险截面的最大弯矩1M为

式中：nF为啮合点处小齿轮所受的法向力；kα为小齿轮啮合点A处压力角；1l为等效悬臂梁长度．

轮齿危险截面的抗弯截面系数1W为

式中：1b为小齿轮轮齿宽度；1s为危险截面宽度．

由于少齿数的小齿轮齿数很少，其危险截面的确定不同于齿数较多的一般渐开线齿轮．为确定齿数为2～6的渐开线小齿轮轮齿的危险截面位置，对小齿轮在一定载荷条件下所受弯曲应力的情况进行了有限元受力分析，如图2所示(z1为齿数)．齿轮所用材料弹性模量均为210MPa，泊松比为0.3．

图2 齿数2～6的小齿轮弯曲应力有限元分析Fig.2 Finite element analysis of bending strength of pinion with z1from 2 to 6

根据有限元分析结果，齿数为2的齿轮危险截面位于两轮齿的中间位置，而齿数3～6的齿轮危险截面基本处于rw1=(rm1+rf1)/2处，rf1为齿根圆半径，rm1为齿根过渡曲线与渐开线工作齿廓的连接点所在圆的半径，如图3所示．根据齿轮加工原理可以求得小齿轮rm1为

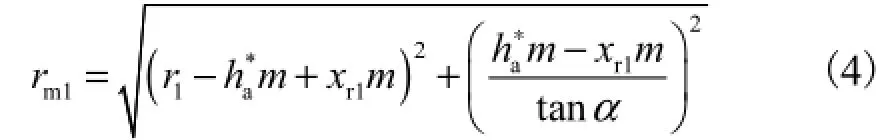
式中：m为齿轮模数；ha*为齿顶高系数；α为分度圆压力角；xr1为小齿轮径向变位系数；r1为小齿轮分度圆半径．

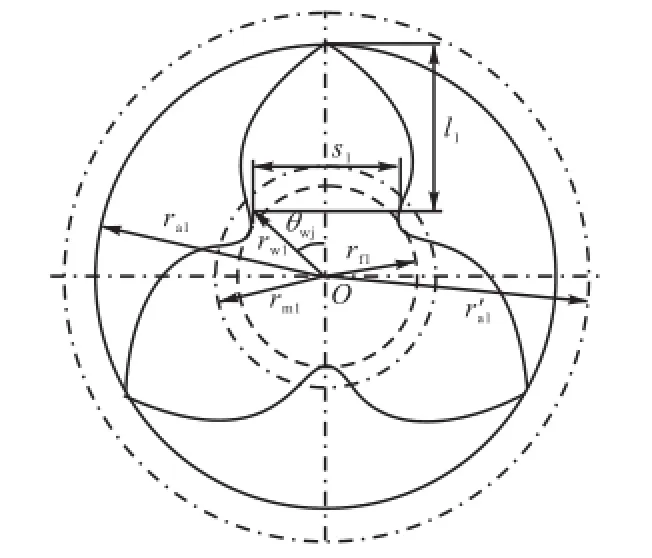
图3 小齿轮危险截面示意Fig.3 Diagram of dangerous cross-section of pinion

由此可得到危险截面宽度s1和等效悬臂梁长度l1分别为

式中：a1r为小齿轮实际齿顶圆半径；wjθ为轮齿危险截面所对应圆心角的1/2，可根据齿轮啮合原理[10-11]求得．

为便于计算，忽略摩擦功耗，将法向力nF用转矩T和小齿轮基圆半径b1r表示为nb1/FTr=，并将式(2)、式(3)、式(5)和式(6)代入式(1)中，可得小齿轮最大弯曲应力F1σ表达式为

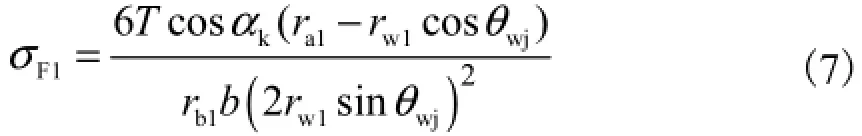
1.2 大齿轮最大弯曲应力分析

大齿轮在齿顶处啮合时其齿根处所受弯曲应力最大．采用30°切线法确定大齿轮危险截面宽度s2及等效悬臂梁长度l2，如图4所示．线段KN的长度即为等效悬臂梁的长度l2，rb2为大齿轮的基圆半径，r2为大齿轮分度圆半径，ra2为大齿轮的齿顶圆半径，θb为齿顶齿厚所对圆心角的1/2，αa2为大齿轮齿顶圆处渐开线齿廓的压力角．假定大齿轮由齿条刀具切削而成，图5为刀具齿廓示意，ha0为刀具中线到刀具齿顶的距离，e为刀具圆角中心到刀具齿廓中心线的距离．

图4 30°切线法Fig.4 30° tangent method

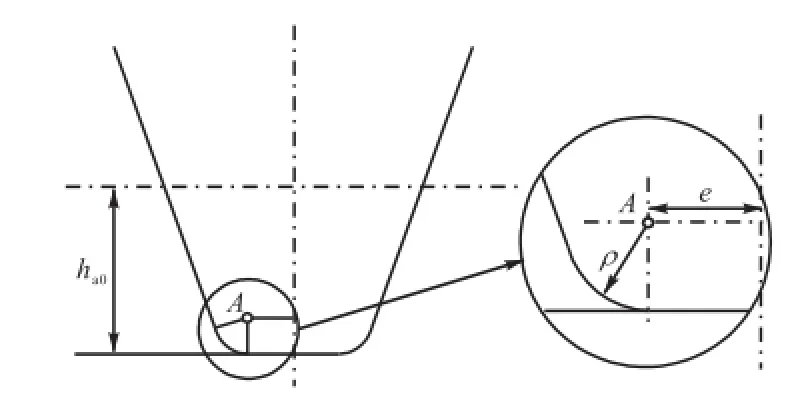
图5 齿轮刀具廓形Fig.5 Profile of gear cutter

图6 所示为刀具切制齿轮的示意[12]，图中P为节点，位置Ⅰ和位置Ⅱ为轮齿转动角度为ϕ时的两个工作位置，在位置Ⅱ时齿根过渡曲线与30°切线的切点S恰好为此时的啮合点．根据刀具和齿轮的几何关系可以求得轮齿危险截面宽度2s及等效悬臂梁长度2l，即

式中：2z为大齿轮齿数；r2x为大齿轮的径向变位系数；θ为在位置Ⅱ时直线AP与位置Ⅰ时坐标轴y的夹角．

θ与ϕ的关系为π/3ϕθ=-，且满足

式中B为刀具圆角中心到齿廓中心线的距离．

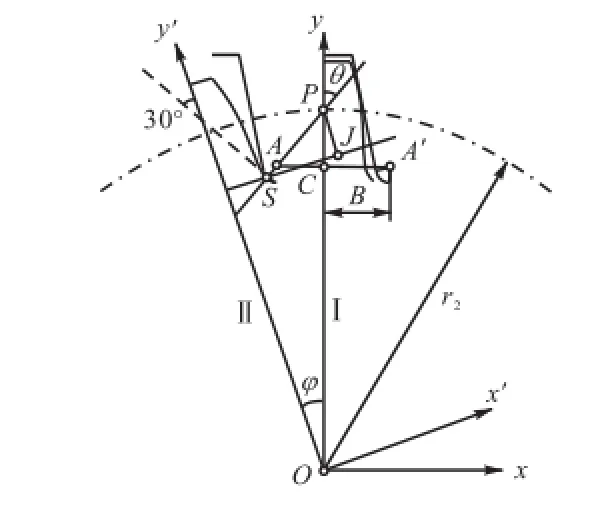
图6 大齿轮2s和2l求解Fig.6 Solution of2s and2lof big gear

在确定危险截面宽度2s及等效悬臂梁长度2l后，可以求得齿根最大弯矩2M和轮齿危险截面的抗弯截面系数2W，即

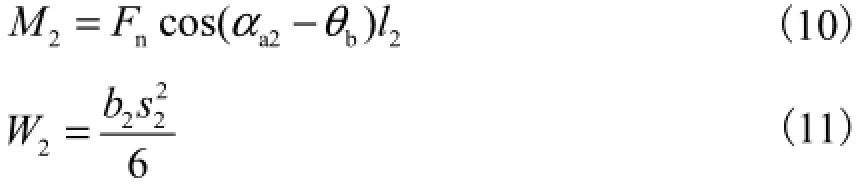
将nb1/FTr=和式(10)、式(11)代入式(1)，得到大齿轮最大弯曲应力

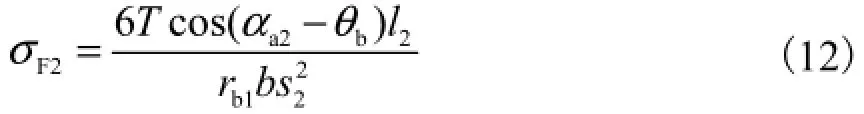
1.3 齿轮副等弯曲强度条件

为设计弯曲强度相同的少齿数齿轮副，应使前述小齿轮和大齿轮的齿根弯曲应力满足

式中Fα为小齿轮和大齿轮材料的许用弯曲应力F1][σ和F2][σ之比，即

将式(7)和式(12)代入式(13)，得到齿轮副等弯曲强度条件式为

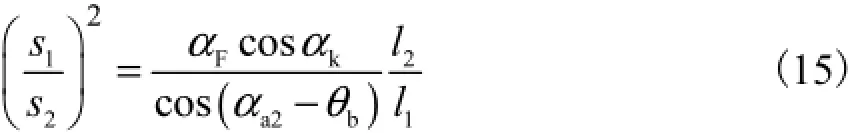
s1、l1、s2和l2分别由式(5)、式(6)、式(8)和式(9)决定．

2 变位系数选择的限制性条件

在少齿数齿轮副变位系数数值的选择上，需要考虑避免轮齿根切、齿廓干涉、齿高缩短、变尖等因素的影响．

2.1 径向变位系数的选择

首先，小齿轮为了避免根切，需满足

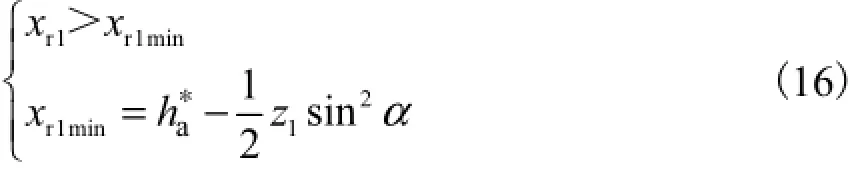
式中xr1min是为避免根切，理论上小齿轮采用的最小径向变位系数．

其次，为了获得高弯曲强度的齿轮传动，应采用无侧隙啮合设计，即小齿轮的节圆齿厚s1′要和大齿轮的节圆齿槽宽e2′相等，即s1′=e′2(或s′2=e1′)．据此可得到满足无侧隙啮合条件的大小齿轮径向变位系数xr1和xr2的关系，即

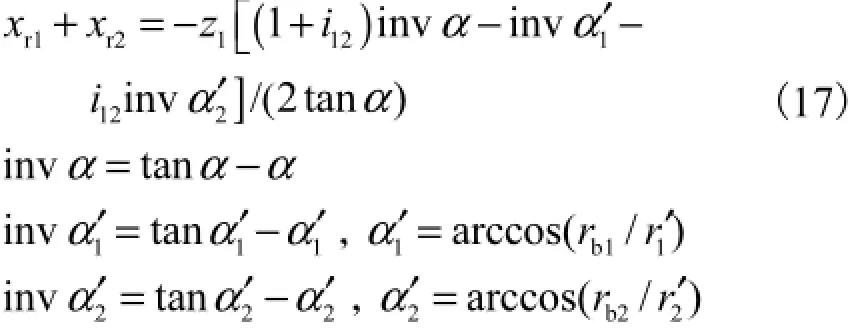
式中：12i为齿轮副传动比，1221/izz=；1α′为小齿轮节圆上的压力角；1r′为小齿轮的节圆半径；2α′为大齿轮节圆上的压力角；2r′为大齿轮的节圆半径．

2.2 切向变位系数的选择

切向变位是指通过改变刀具的齿厚来改变切制齿轮的齿厚，切制出的齿轮称为切向变位齿轮．刀具齿厚的改变量称为切向变位量，大小为xτm ，其中m为模数，xτ为切向变位系数．本文设定刀具齿厚减小，被切制齿轮齿厚增大时刀具切向变位系数为正变位(即xτ＞0)．切向变位的刀具如图7所示．

在少齿数齿轮传动中，切向变位的目的是在无侧隙啮合条件下协调大小齿轮轮齿的齿厚．由此也可获得大小齿轮轮齿具有相同或接近的弯曲强度．一般情况下是优先增加小齿轮的齿厚．但由齿轮啮合原理可知，如果小齿轮的齿厚增加过多，则会使与之啮合的大齿轮的齿厚减小过大，造成大齿轮弯曲应力过大．图8所示为齿数60的大齿轮轮齿齿形随切向变位系数变化的情况(2xτ为大齿轮切向变位系数)．

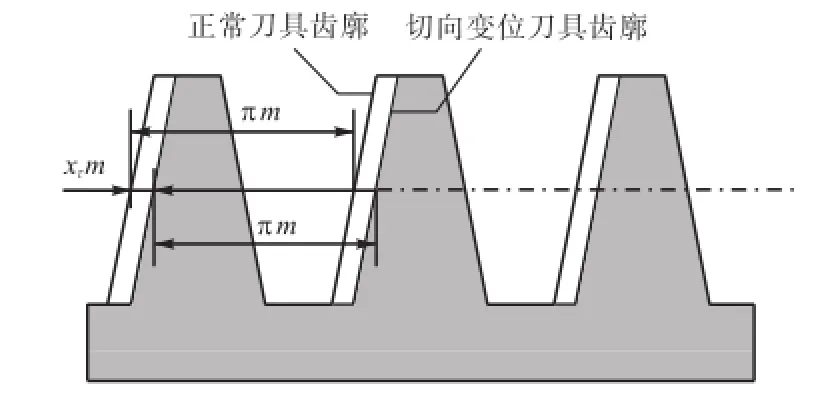
图7 切向变位刀具示意Fig.7 Cutter with tangent modification

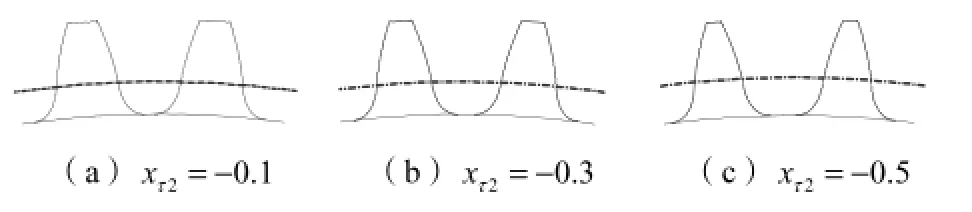
图8 切向变位系数对大齿轮齿形的影响Fig.8 Tangent modification influence on the big gear profile

从小齿轮方面考虑，如果切向变位系数过大则会出现图9(a)所示的齿廓干涉(此时对应的刀具齿廓如图9(c)所示，也不完整)，使轮齿齿廓的加工和啮合传动不能正常进行．

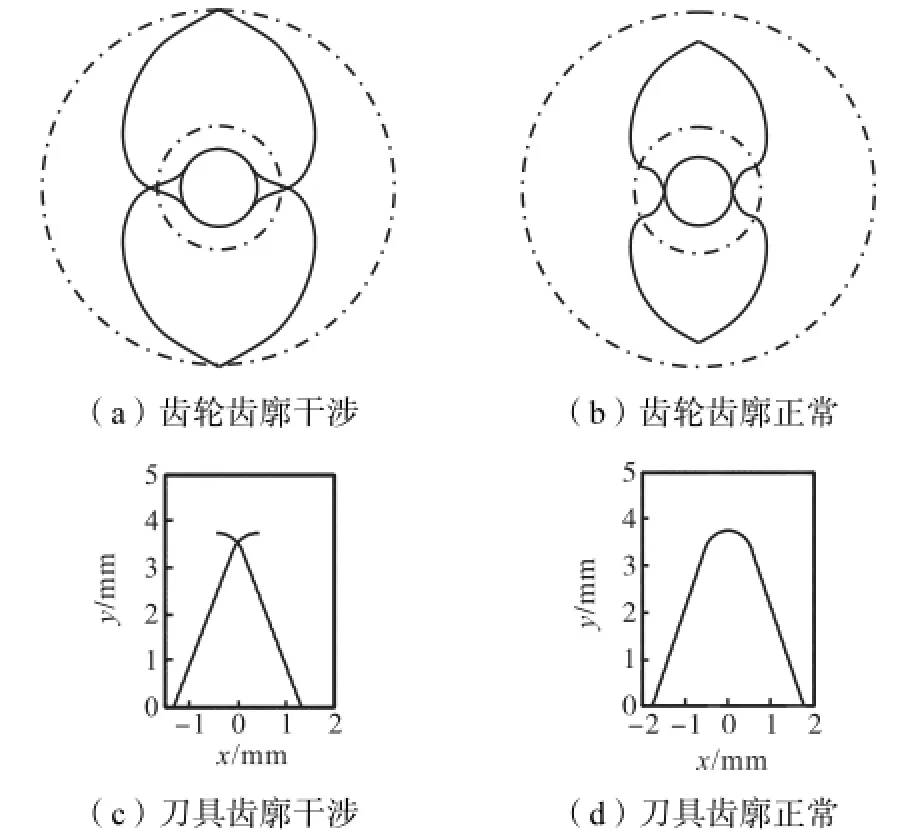
图9 切向变位与齿廓干涉刀具齿廓Fig.9 Profile of tangent modification gear and cutter

为了避免因过大的切向变位使小齿轮齿廓出现图9(a)的情况，需要对切向变位系数加以限制，使齿条刀具齿廓相对完整，防止出现图9(c)中刀具齿顶圆角相交的情况．为此，就要使图5中的刀具圆角中心到刀具齿廓中心线的距离0e≥，即需满足

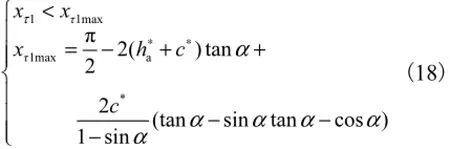
式中：xτ1为小齿轮切向变位系数；xτ1max为保证切制小齿轮刀具正常齿廓的最大切向变位系数；c∗为齿轮顶隙系数．

2.3 小齿轮齿高分析

小齿轮采用较大的径向变位，会使轮齿出现变尖、齿高缩短、齿轮副啮合重合度减小的现象；而切向正变位可使小齿轮齿厚加大，并可增加齿高或减小齿高缩短的程度．

为了保证良好的啮合性能，应通过采用合理的径向和切向变位系数使小齿轮保持一定的齿高．为此，对小齿轮轮齿尖点到理论齿顶圆的距离进行研究．在图10中，点F表示小齿轮齿廓的尖点，在坐标系Oxy中的坐标为(xa1,ya1)，且xa1=0，则小齿轮轮齿尖点与理论齿顶圆的距离f可表示为在通过选取切向变位系数的齿形设计中，应使f尽量选取较小值．

图10 小齿轮轮齿尖点与理论齿顶圆的距离Fig.10Distance top point of pinion and theoretical addendum circle

3 计算变位系数的数学模型

3.1 数学模型的建立

通过上述对如何选择径向变位系数和切向变位系数的研究，得到了高强度的渐开线少齿数齿轮副变位系数应满足的条件：①满足大小齿轮轮齿等弯曲强度条件式(15)的要求；②满足齿轮副无侧隙啮合，大小齿轮的径向变位系数之和应满足条件式(17)；③径向变位系数的数值应满足避免根切的要求；④切向变位系数的数值应满足避免出现齿廓干涉的现象；⑤在满足上述条件之后，选取小齿轮轮齿尖点到理论齿顶圆的距离最小的变位系数组合．

为此，可采用优化方法求解最优变位系数组合．将式(19)作为目标函数，求其最小值，将等弯曲强度条件式(15)、避免根切条件式(16)、无侧隙啮合条件式(17)、切向变位系数选择式(18)作为约束条件，建立优化数学模型

3.2 计算实例

以大小齿轮齿数分别为60和4、模数1.5,mm、中心距为48.3,mm、使用相同材料强度的齿轮副为例，材料弹性模量为210MPa，泊松比为0.3．采用了3种变位系数设计方案：①单纯为了避免小齿轮的根切，只采用径向变位；②在①的基础上增加切向变位、增大小齿轮齿厚，给定切向变位系数xτ1=0.1，xτ2=-0.1；③采用式(20)模型计算得到齿轮副的变位系数．具体计算结果见表1．在小齿轮转矩为2.8×102N·mm 的条件下，用有限元软件进行了轮齿应力分析，得到齿轮副最大的应力即齿根弯曲应力，结果如表1所示．采用3种变位系数的齿轮副端面齿形，如图11所示．

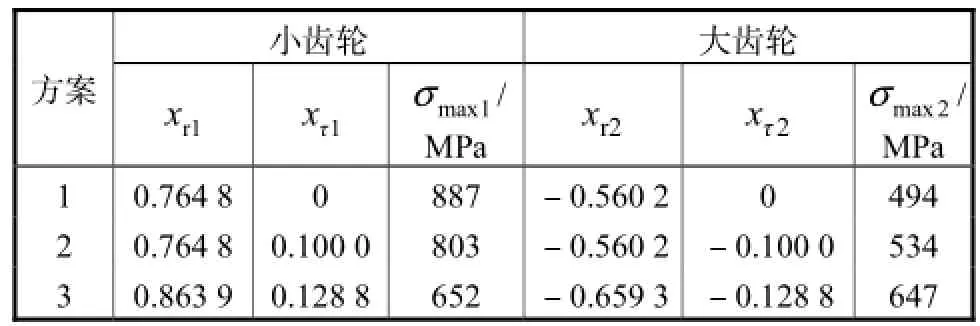
表1 齿轮副变位系数选取与最大弯曲应力Tab.1 Selection of gear modification coefficients and maximum bending stress

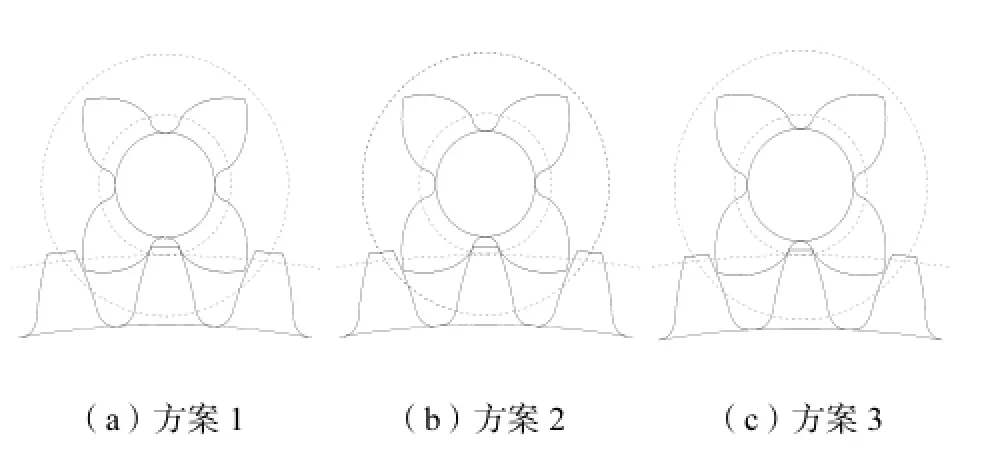
图11 齿轮副端面齿形Fig.11 Transverse tooth profile of gear pair

图11 中，3个方案的小齿轮分度圆齿厚分别为4.199,mm、4.499,mm和4.802,mm，有限元应力分析表明，采用切向变位的齿轮副，大小齿轮的最大弯曲应力差值明显减小，而采用本文模型式(20)计算齿轮副径向和切向变位系数后，大小齿轮的最大应力差值很小，接近于等弯曲强度设计，如图12所示．

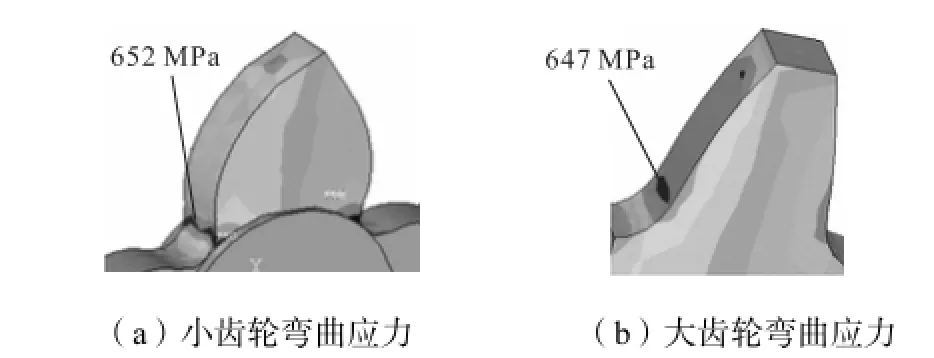
图12 优化求解变位系数的齿轮副应力分析Fig.12Stress analysis of gear pair with the optimization modification coefficient

4 结 论

(1) 在轮齿等弯曲强度设计条件下，渐开线少齿数齿轮副的径向变位系数和切向变位系数的选择应协同考虑，并满足一定的函数关系．

(2) 径向变位系数的选择需要考虑轮齿根切和齿轮副无侧隙啮合两方面因素，即小齿轮的径向变位系数应满足避免根切的条件，而齿轮副径向变位系数之和要满足一定函数关系．

(3) 切向变位系数的选择需要考虑切向变位对大小齿轮啮合情况与弯曲强度的相互影响．小齿轮切向变位过大会使大齿轮的齿厚过小，削弱大齿轮的弯曲强度，同时有可能引起小齿轮齿根齿廓干涉的问题．

(4) 对于齿数、模数确定的少齿数齿轮副，通过建立变位系数的数学模型，可获得轮齿副等弯曲强度条件下大小齿轮径向和切向变位系数的最佳组合．

［1］ Ishibashi Akira，Yoshino Hidehiro，Nakashima Iwao. Design and manufacturing processes and load carrying capacity of cylindrical gear pairs with 2 to 4 pinion teeth for high gear ratios(1st report design and manufacture and surface durability of gears with 2 to 3 pinion teeth)[J]. Transactions of the Japan Society of Mechanical Engineers：Series C47，1981，416：507-515.

［2］ Ishibashi Akira，Yoshino Hidehiro. Design manufacture and load carrying capacity of novikov gears with 3—5 pinion teeth for high gear ratios(1st report，design，manufacture and power transmission efficiency)[J]. Transactions of the Japan Society of Mechanical Engineers：Series C49，1983，447：2039-2047.

［3］ Chen Chien-Fa，Tsay Chung-Biau. Tooth profile designfor the manufacture of helical gear sets with small number of teeth[J]. International Journal of Machine Tools & Manufacture，2005，45(12/13)：1531-1541.

［4］ Pan Fengzhang，Jing Xiubing，Meng Caifang. Involute gearing with small tooth number[J]. Chinese Mechanical Engineering Society：English Edition，2004，17(Suppl)：113-115.

［5］ 蒋 军. 双向变位少齿数圆柱齿轮副：中国，ZL 94208649. X[P]. 1995-05-24.

Jiang Jun. Little Teeth Number Cylindrical Gear Pair with Bilateral Modification：China，ZL94208649.X [P]. 1995-05-24(in Chinese).

［6］ 王树平. 平面啮合少齿数齿轮副齿形设计研究[D]. 天津：天津大学机械工程学院，2012.

Wang Shuping. Study on the Tooth Profile Design for Planar Meshed Gear Sets with Small Number of Teeth[D]. Tianjin：School of Mechanical Engineering，Tianjin University，2012(in Chinese).

［7］ 赵向飞，田 燕，刘红旗，等. 少齿数齿轮变位系数的研究[J]. 合肥工业大学学报：自然科学版，2013，36(6)：655-659.

Zhao Xiangfei，Tian Yan，Liu Hongqi，et al. Study of modification coefficients of gear with fewer teeth[J]. Journal of Hefei University of Technology：Natural Science，2013，36(6)：655-659(in Chinese).

［8］ 孙 伏，张 杰. 渐开线少齿数齿轮弯曲疲劳应力计算系数的研究[J]. 机械设计与制造，2010(6)：40-41.

Sun Fu，Zhang Jie. The research of coefficient in calculating bending fatigue stress of involute gear with fewer teeth[J]. Machinery Design & Manufacture，2010(6)：40-41(in Chinese).

［9］ 齿轮手册编委会. 齿轮手册[M]. 北京：机械工业出版社，2000.

Gear Manual Editing Committee. Gear Manual[M]. Beijing：China Machine Press，2000(in Chinese).

［10］ 吴序堂. 齿轮啮合原理[M]. 西安：西安交通大学出版社，2009.

Wu Xutang. Principle of Gear Meshing[M]. Xi’an：Xi’an Jiaotong University Press，2009(in Chinese).

［11］ 李特文 F L. 齿轮几何学与应用理论[M]. 上海：上海科学技术出版社，2008.

Litvin F L. Gear Geometry and Applied Theory [M]. Shanghai：Shanghai Science and Technology Press，2008(in Chinese).

［12］ 刘平娟，孔伟程. 渐开线齿轮齿形系数的计算公式[J]. 机械设计，1984(4)：66-69.

Liu Pingjuan，Kong Weicheng. Calculation formula of coefficient of involute gear tooth profile[J]. Journal of Machine Design，1984(4)：66-69(in Chinese).

(责任编辑：金顺爱)

Modification of Involute Gear Pair with Fewer Teeth Based on Equal Bending Strength

Sun Yuehai1,2，Liu Yanfeng1，Duan Luqian3，Ge Nan1
(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300072，China；2. Engineering Research Center of Light-Duty Power Machine of Ministry of Education，Tianjin University，Tianjin 300072，China；3. Department of Mechanical Engineering，Academy of Armored Forces Engineering，Beijing 100072，China)

To solve the problem of the weak strength of involute gear pair with fewer teeth，research is doneon the selection of its addendum modification coefficient and tangent modification coefficient，taking the planar involute gear pair with fewer teeth as the research object with the designing intention of enhancing the bending strength of pinion and obtaining the same or approximately bending strength of gear pair. By the analyzing the maximum bending stress of gear pair，it is deduced that addendum modification coefficient and tangent modification coefficient of gear pair should be related functionally. Two factors must be considered for the selection of addendum modification coefficient，i. e. undercut and no lateral clearance meshing. Theaddendum modification coefficient of pinion must meet the condition that undercut is avoided，and the sum of addendum modification coefficients of gear pair must be in a certain functional relation. The selection of tangent modification coefficient need to consider the mutual influence between tangent modification and meshing of gear pair and bending strength. If the tangent modification coefficient of the pinion is excessively big，the tooth thickness of gearwheel will be reduced，its bending strength be weakened，and the tooth profile and root of the pinion be interfered. According to the above conditions，for involute gear pair with fewer teeth with ascertained tooth number and modulus，the optimum modification coefficients are found basedon equal bending strength through establishing the mathematical model for solving the modification coefficients.

gear；gear pair with fewer teeth；bending strength；modification coefficient

TH132.413

A

0493-2137(2014)11-1001-07

10.11784/tdxbz201311008

2013-11-04；

2013-12-03.

国家自然科学基金资助项目(51175369)．

孙月海（1964— ），男，博士，教授.

孙月海，yuehaisun@tju.edu.cn.

时间：2014-01-03.

http：//www.cnki.net/kcms/doi/10.11784/tdxbz201311008.html.