爆炸作用下RC柱损伤快速评估模型

李忠献，钟 波，师燕超

爆炸作用下RC柱损伤快速评估模型

李忠献，钟 波，师燕超

(滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072)

基于BP神经网络，以7个结构参数和2个荷载参数作为输入，损伤值作为输出，建立了爆炸作用下钢筋混凝土(RC)柱损伤的快速评估模型．在模型中，采用以精细化有限元模拟得到的1,032组RC柱损伤的数据训练网络，采用遗传算法和粒子群算法优化网络的初始权值和阈值，并以216个新损伤样本对模型的预测能力进行测试．研究表明，所建立的评估模型能够较准确地用于爆炸作用下RC柱损伤的快速评估；所得到的损伤分区图可以有效并直观地用于RC柱的爆炸风险评估．

爆炸作用；钢筋混凝土柱；损伤评估；风险评估；BP神经网络

爆炸作用下RC柱的损伤评估对结构的防护设计具有重要意义．目前，常用等效单自由度体系或精细化有限元模拟模型进行RC柱的损伤预测．精细化有限元模拟模型的预测结果，能反映RC柱在爆炸作用下的各种破坏模式，计算精度高，但计算效率低，仅适用于对特定的或少量的RC柱的损伤评估，而无法用于对大量RC柱的损伤评估，即不适合于工程应用．相对而言，等效单自由度体系通过一些简化假定，将构件等效为一个质量-弹簧体系[1]，求解参数少，计算效率高，能快速地进行大量RC柱的损伤预测，但其中的一些简化假定(如变形模式)使得求解精度较低，尤其是在构件高阶响应贡献较大时[2]．因此，等效单自由度体系一般多用于以弯曲破坏为主的构件，虽然Krauthammer等[3]提出了同时考虑弯曲、剪切与张力膜效应的等效单自由度体系，但是对使用者要求较高，抗力函数获取难度较大．

针对等效单自由度体系与精细化有限元模拟模型的缺点，Bao等[4]使用LS-DYNA研究了RC柱在爆炸作用下的非线性动力响应，并通过参数分析拟合了一个预测轴向残余承载率的公式，然而由于该公式中含有爆炸作用后构件跨中的残余变形，仍然需要建模进行求解．Shi等[5]对于判定爆炸作用下RC柱破坏程度，提出了一种新的基于竖向剩余承载力的破坏准则，建立了爆炸作用下RC矩形柱压力-冲量(p-I)曲线的预测公式，进一步建立了RC柱基于p-I曲线的损伤程度评估新方法，适于工程应用．因此，考虑影响爆炸作用下RC柱损伤程度的各参数，建立各影响参数与RC柱损伤程度的非线性映射关系，可实现对RC柱损伤的快速评估．影响爆炸作用下RC柱损伤程度的因素很多，很难建立一个较为通用的预测公式．

人工神经网络对多参数影响的复杂非线性关系可进行合理描述，已在土木工程领域得到了较广泛的应用[6-7]，尤其在结构健康监测方面[8]，但在结构抗爆领域还仅有一些初步探索．Ibrahim等[9]基于人工神经网络，建立了近爆作用下RC板的损伤预测模型，能较准确地预测损伤尺寸，与工程中使用的设计图表吻合良好．Flood等[10]结合粗粒度仿真方法与人工神经网络，建立了模拟复杂环境中爆炸波传播的高效模型，兼具效率与通用的优点，弥补了经验方法与计算流体动力学方法的不足．Stewart[11]基于人工神经网络，建立了爆炸作用后钢柱剩余承载力的快速评估方法，可用于爆炸风险评估，为初步防护设计提供安全距离，但由于模型的输入参数太少，训练样本量偏少，损伤预测精度较低．

本文基于BP神经网络，充分考虑影响爆炸作用下RC柱损伤程度的各参数，通过精细化有限元模拟模型，得到足够的有代表性的损伤样本值，以此作为网络的训练样本，然后以均方误差为适应度函数，利用遗传算法和粒子群算法优化网络的初始权值和阈值，建立爆炸作用下RC柱动力响应的主要参数与RC柱损伤值之间的非线性映射关系，以快速评估爆炸作用下RC柱的损伤程度以及RC柱的爆炸风险．

1 基于BP神经网络的损伤快速评估模型

1.1 BP神经网络模型

人工神经网络(artificial neural networks，ANNs)是一种模拟生物神经网络行为特征，进行分布式并行信息处理的数学模型，已被广泛用于模式识别、信号处理、专家系统及优化组合等领域．神经元是人工神经网络的基本信息处理单位，其模型如图1所示，由一组连接、一个加法器、一个激活函数以及外部偏置组成，将大量的神经元进行连接，即可构成人工神经网络．神经元可表示为

式中：xi(i=1,2,…,m)为网络的输入，m为输入参数的个数；wik(i=1,2,…,m)为网络的权值，k表示第k个输出参数；ku表示输入的线性组合；kb为网络的阈值；ky为网络的输出．

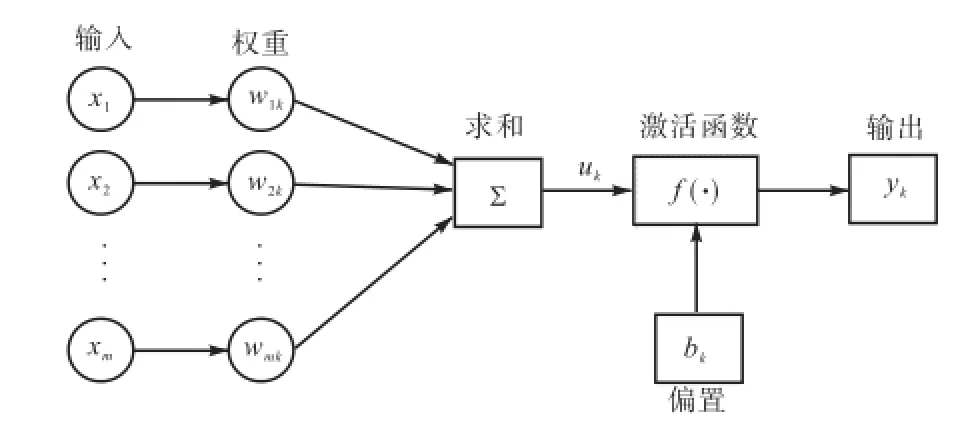
图1 神经元模型Fig.1 Neuron model

BP神经网络是目前研究最为成熟、应用最为广泛的人工神经网络模型之一．它采用误差反向传播算法调整各层神经元之间的连接权值，以使网络达到更好的逼近能力．该算法的实质是根据神经网络实际输出与期望输出之间误差的负梯度方向，从后往前逐层地迭代修正各层神经元之间的连接权值．网络的期望输出值与实际输出值之差为()ew，网络的学习误差函数为()Ew，训练网络的过程便是不断地调整权值和阈值使得误差()Ew降低到允许的范围内．当得到满足条件的权值和阈值后，便能使用该网络进行预测．()ew和()Ew可表示为

式中：t为期望输出向量；o(w)为网络实际输出向量．

L-M算法[12]为标准BP算法的改进形式，通过将Hessian矩阵分解为Jacobian矩阵乘积后求逆以减少计算复杂度．每次迭代的权值或阈值可按下式计算，即

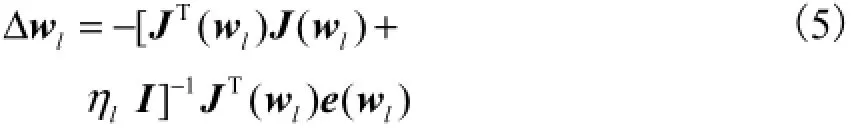
式中：l为迭代的次数；I为单位方阵；J为网络误差函数的雅克比矩阵；lη为控制收敛的参数，当其为0时，L-M算法即变为牛顿法．

1.2 损伤评估神经网络的输入参数

考虑影响爆炸作用下RC柱动力响应的各参数，选用9个参数作为RC柱损伤评估BP神经网络的输入参数，其中7个为结构参数，分别为截面宽度b、截面高度h、构件长度L、箍筋配箍率sρ、纵筋配筋率lρ、轴压比μ(本文取模型施加的轴向压力与混凝土轴心抗压强度标准值和截面积乘积的比值)和混凝土轴心抗压强度标准值cf；2个为荷载参数，即炸药质量m和比例距离Z．表1列出了各输入参数及其取值范围．

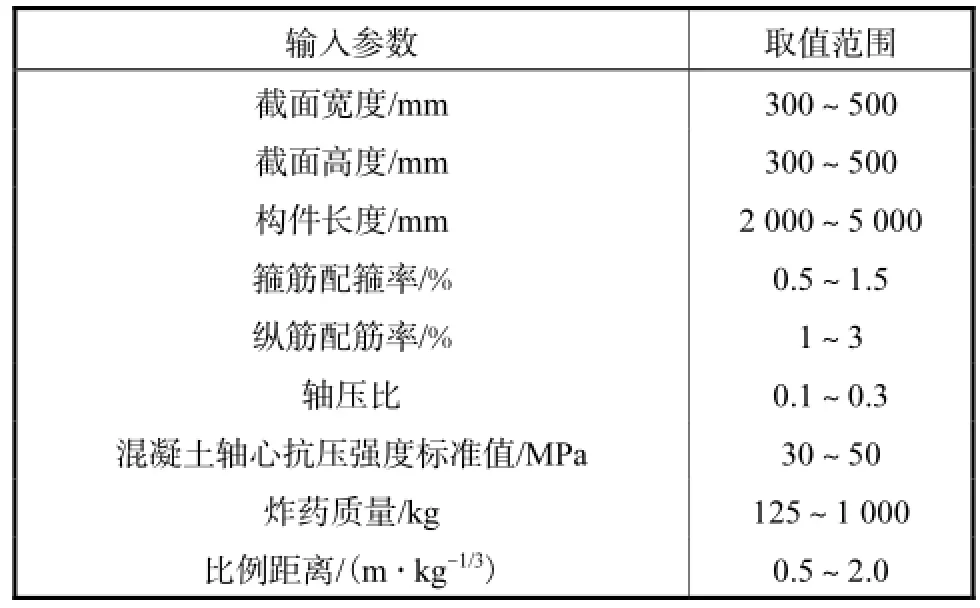
表1 损伤评估网络的输入参数及取值范围Tab.1 Input parameters and their range of damage assessment network

1.3 RC柱损伤评估神经网络模型

由于RC柱主要为竖向承重构件，其竖向承载力的退化程度可以用于评估各种破坏模式的损伤，因此，采用Shi等[5]提出的RC柱基于竖向剩余承载力的损伤准则，即定义损伤指数D为

式中：rP为爆炸作用后RC柱的剩余承载力；pP为柱顶初始施加的轴向力；NP为柱的初始轴向承载力．

RC柱的有限元模型与文献[5]相同，模型网格尺寸25,mm，混凝土与钢筋采用分离式建模，混凝土用*Mat_Concrete_Damage_Rel3模拟，钢筋用*Mat_ Plastic_Kinematic模拟．爆炸荷载通过*Load_Blast施加，炸药离地面的高度为1,m．首先根据相应的轴压比在柱顶施加一恒定的轴力，待达到静力平衡后，炸药起爆，RC柱在爆炸作用下产生一定的损伤，当重新达到静力平衡时，对柱顶进行位移控制加载，直到彻底破坏，得到整个过程RC柱的轴力时程曲线如图2所示，根据该曲线的特点，得到柱的竖向剩余承载力rP，进而求得爆炸作用产生的损伤值．

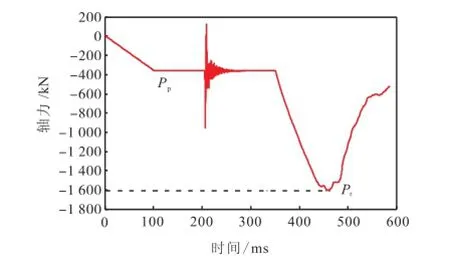
图2 RC柱轴力时程曲线Fig.2 Time history of axial force of RC columns

据此计算RC柱的损伤值，共得到1,032个样本数据，其损伤值在0.032,1～1之间．

由Kolmogorov定理可知，一个3层前馈型神经网络足以完成任意的n维到m维的映射，即选用一个隐层的BP神经网络便可以满足任意非线性目标函数逼近的要求[13]．由于输入、输出层神经元的数量是确定的，因此，确定隐层神经元的数量就可以确定网络结构．隐层神经元的数量与网络的计算复杂度联系密切，如果隐层神经元数量偏少，网络不具备必要的学习能力和信息处理能力，会呈现出学习误差下降缓慢，甚至出现达不到目标精度的不拟合现象；若隐层神经元的数量过多，会造成网络结构庞大、网络运算和泛化能力降低等问题．在反复试验的基础上，本文中隐层神经元数量确定为9，此时所得到的均方误差最小．BP神经网络结构如图3所示．

图3 损伤评估BP神经网络Fig.3 BP neural networks for damage assessment

为了提高网络模型的泛化推广能力，防止模型出现过拟合现象，网络训练采用提前终止法．将1,032组数据随机分成训练集、确认集和测试集，其中，训练集占70%(722个样本)，确认集与测试集各占15%(共310个样本)．由于网络训练的初始权值和阈值是随机生成的，不合适的初始值易使网络陷入局部极小点，因此，本文通过遗传算法和粒子群算法寻求BP神经网络的最优初始权值和阈值，适应度函数取为网络的均方误差．图4为遗传算法和粒子群算法优化过程中适应度值的变化，从中可以看出，粒子群算法使网络的均方误差更小，其优化效果较遗传算法好．以粒子群算法优化得到的初始权值和阈值对网络进行训练，当该网络的训练次数为86时，确认样本集的误差连续增加的次数已达到预先设定的6次，此时，为了防止网络出现“过适配”，网络训练提前终止，返回训练次数为80次时的权值和阈值，如图5所示．图6～图8分别给出了预测模型对训练集、确认集与测试集数据的拟合效果，从中可以看出，所有数据点基本都在理想参考线y＝x的附近，相关性系数R均为0.997，表明该模型对1,032组数据有较好的拟合效果．

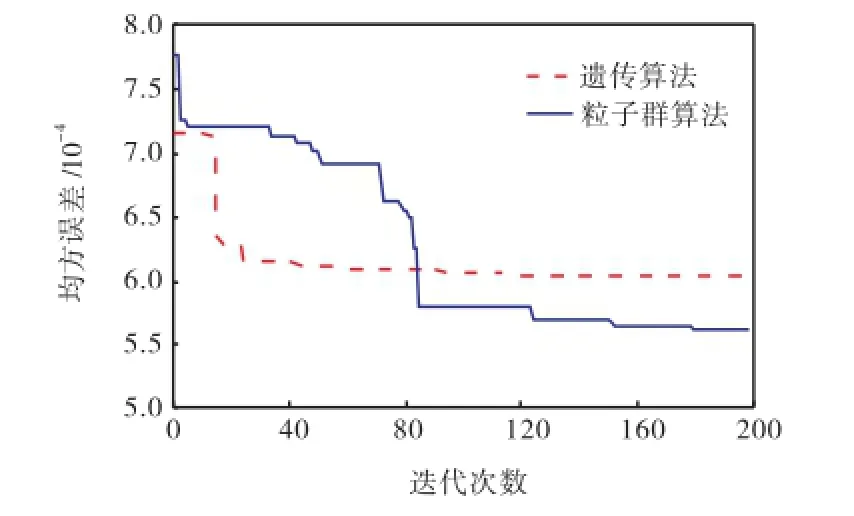
图4 网络优化算法的适应度值变化过程Fig.4 Change process of fitness value of different optimization algorithms

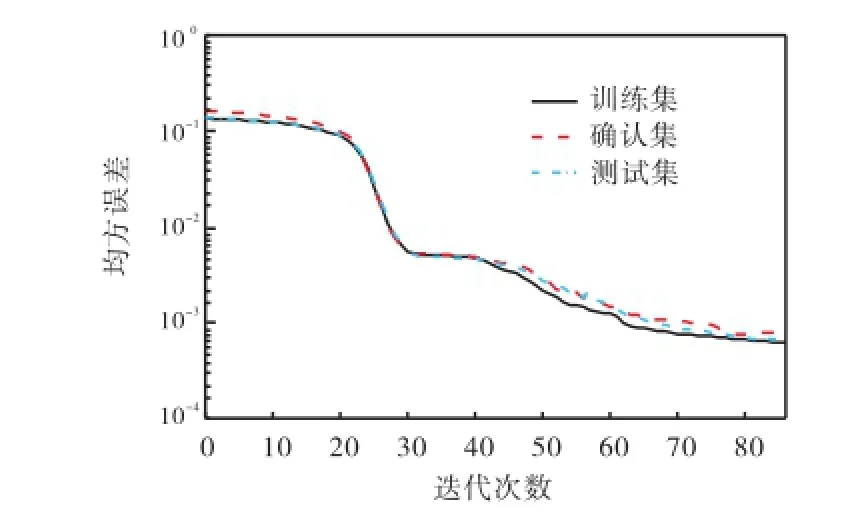
图5 网络的训练过程Fig.5 Training process of the networks

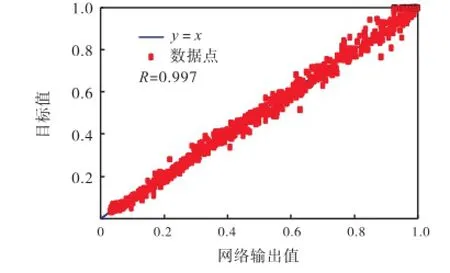
图6 训练集的拟合结果Fig.6 Fitting results of training set

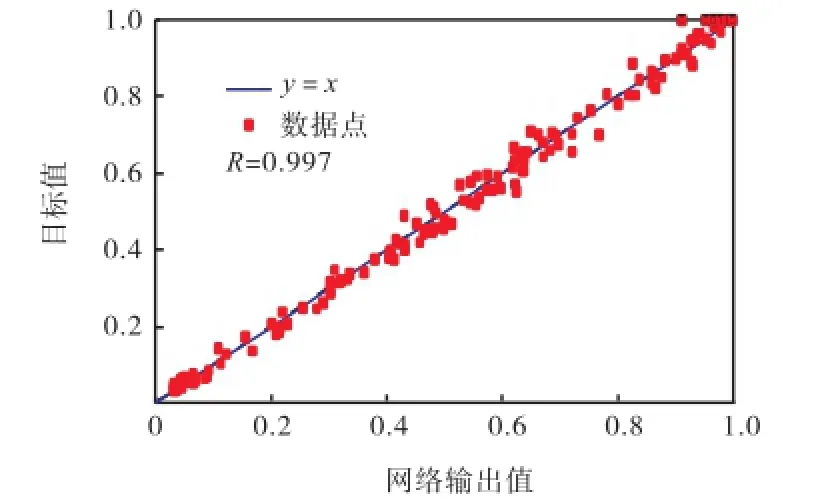
图7 确认集的拟合结果Fig.7 Fitting results of validation set

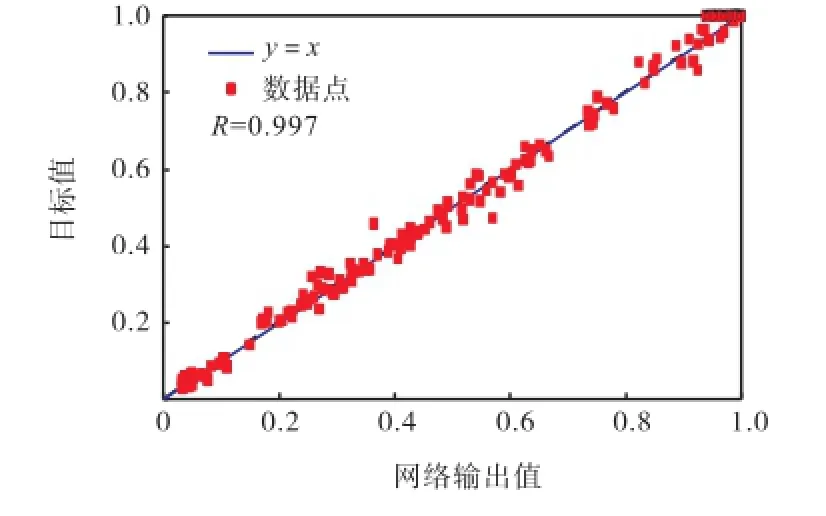
图8 测试集的拟合结果Fig.8 Fitting results of testing set

1.4 损伤评估神经网络模型的性能评价

为评价本文所建立的RC柱损伤评估神经网络模型的预测能力，采用权重法计算神经网络模型输入参数对输出结果的相对重要性指数RI，即各个输入神经元对输出神经元的权重贡献[14]为

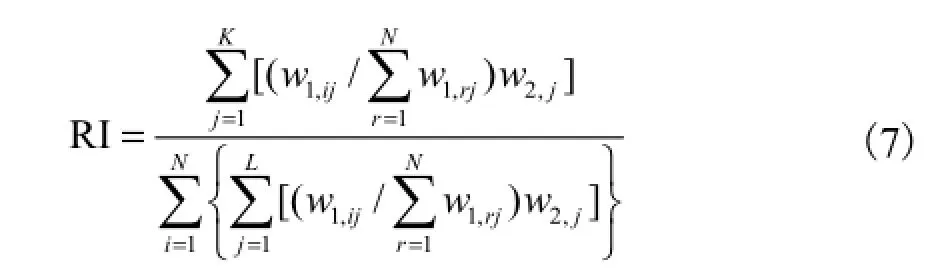
式中：1,ijw为第i个输入神经元与第j个隐层神经元的连接权重；2,jw为第j个隐层神经元与输出神经元的连接权重；K为隐层神经元的数量；N为输入神经元的数量．

表2给出了由式(7)计算得到的各输入参数的相对重要性指数．由此可以看出，比例距离Z的相对重要性达到了36.7%，其对爆炸作用下RC柱的损伤值影响最为显著，即比例距离发生较小的变化也可能导致损伤值发生较大的变化．因此，为了验证本文所建立的损伤预测模型具有较好的泛化推广能力，应在测试样本集中尽量多包含1,032个训练样本中未使用的比例距离．

通过第1.3节的方法计算得到216个新损伤样本，炸药质量M为1,000,kg，其他输入参数限定在表1的取值范围内．图9为216个新样本在比例距离-损伤值空间的分布，其中含有大量训练样本中未使用的比例距离值(训练样本中用到的比例距离为0.5m/kg1/3、1.0m/kg1/3和2.0m/kg1/3)．基于前文建立的预测模型对这216个样本的输出进行预测，得到的结果如图10所示，有限元模拟结果与网络预测结果组成的坐标点基本分布在理想参考线y＝x附近，相关性系数R达到了0.997，表明本文模型具有良好的预测能力．图11和图12分别为损伤预测值与期望值的绝对误差及绝对误差频数分布直方图．其中最大绝对误差为0.096，约94%的数据点绝对误差都控制在0.04以内．

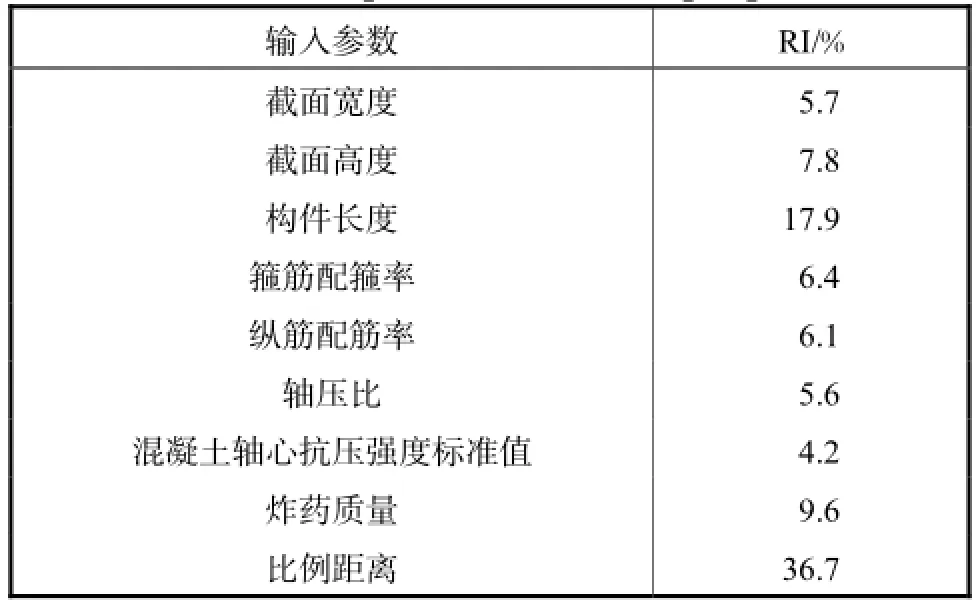
表2 输入参数的相对重要性指数Tab.2 Relative importance index of input parameters

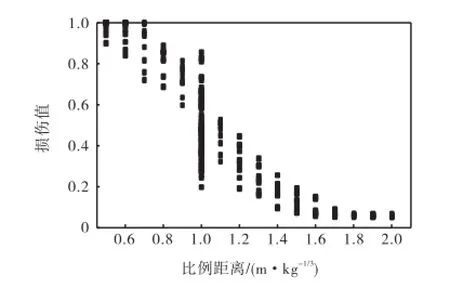
图9 216个新损伤样本的分布Fig.9 Distribution of 216 new damage samples

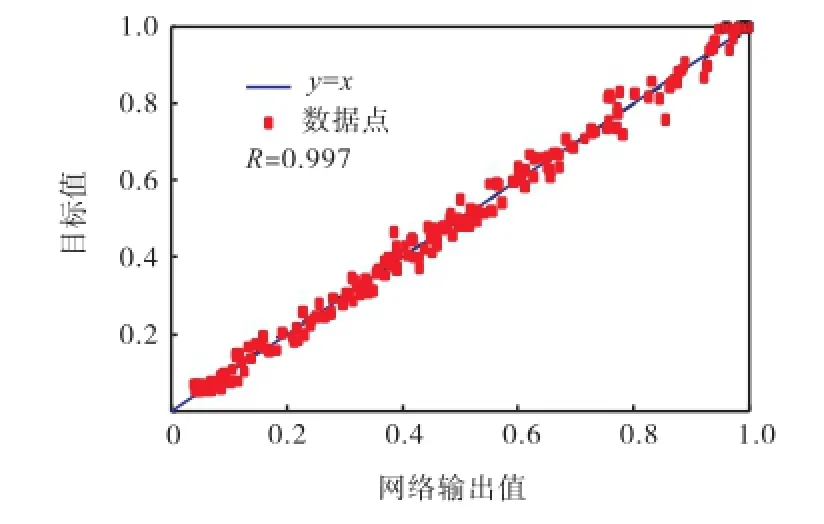
图10 216个新损伤样本的拟合结果Fig.10 Fitting results of 216 new damage samples

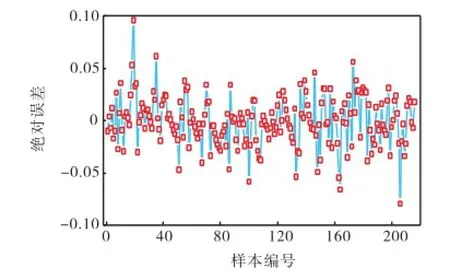
图11 网络预测的绝对误差Fig.11 Absolute error of predictions

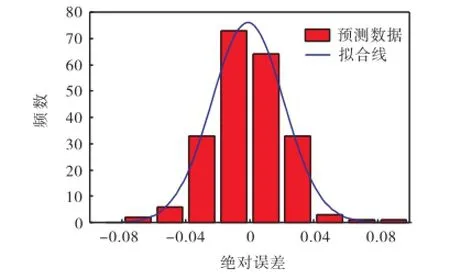
图12 绝对误差频数分布直方图Fig.12 Frequency distribution histogram of absolute error

2 RC柱的爆炸风险评估

对结构或构件的潜在爆炸风险进行评估通常需要在一个相对快速的分析模型框架内进行．目前大部分的爆炸风险评估模型都是基于等效单自由度体系，但由于等效单自由度体系的一些固有缺陷，必然导致分析结果的可靠性受到影响．本文建立的损伤快速评估模型兼具精细化有限元模型准确性高与等效单自由度体系效率高的优点，非常适合于RC柱的爆炸风险评估．下面通过一个算例说明本文模型用于爆炸风险评估的过程．

[11]，考虑某临街的重要RC结构，如图13所示，其底层柱的参数为：b＝h＝400,mm，L＝3,000,mm，ρs=0.5%，ρl=1%，μ=0.1，fc= 30MPa．结构面临的可能威胁为汽车炸弹袭击，考虑其等效TNT质量为200～1,000,kg．结构与街道间可以设置混凝土防撞栏以提供一定的安全防护距离SD(safe distance)，现在需要对该结构进行爆炸风险评估并确定一个合理的SD值．

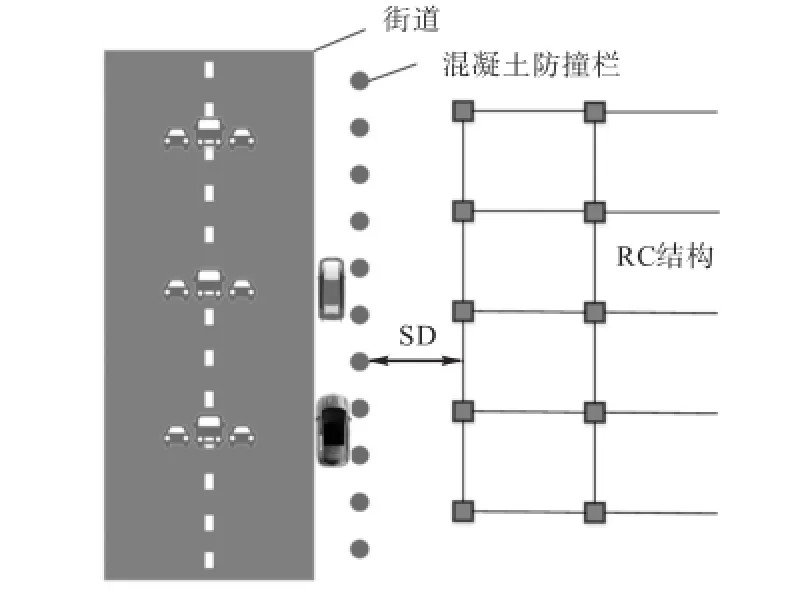
图13 临街RC结构爆炸威胁算例Fig.13Blast threat scenario example of RC structure along the street

按文献[5]中提供的方法，将爆炸作用下RC柱的损伤程度分为4个等级：D＝0～0.2，轻度损伤；D＝0.2～0.5，中度损伤；D＝0.5～0.8，重度损伤；D＝0.8～1.0，倒塌．设轻度损伤和中度损伤为能够接受的损伤状态．在表1中参数m和Z的取值范围内，将其分别等分为s和n份，本算例取s＝175，n＝150，即m-Z空间中总共得到26,576个点；然后通过Matlab编制程序生成模型的输入文件，使用本文建立的快速损伤评估模型预测相应的损伤值；最后将损伤值绘制在m-Z空间，并根据损伤程度分级得到了图14所示的RC柱损伤分区．若等效TNT质量为512,kg的汽车炸弹在距离结构7,m处发生爆炸，反映到m-Z空间的损伤分区图中，如图14中黑色菱形点所示，该菱形点落在了重度损伤区域，表明结构的底层RC柱处于重度损伤状态，超出了可接受的损伤程度，需要将混凝土防撞栏设置在7,m以外的某处以减小损伤程度．

本算例中爆炸威胁为等效TNT质量200～1,000,kg，考虑其上限1,000,kg，并将可接受损伤程度上限在m-Z空间中用黑色圆点表示，对应的比例距离约为1.24,m/kg1/3，进而可以求得合理的安全防护距离SD为12.4,m．可见，本文模型用于RC柱爆炸风险评估的过程可以概括为：通过Matlab绘制特定RC柱在m-Z空间的损伤分区图；根据可能的具体爆炸威胁确定其损伤程度或者偏保守地根据可接受损伤程度上限确定一个合理的安全距离SD．

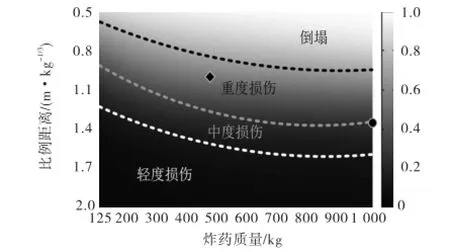
图14 爆炸作用下RC柱损伤的分区Fig.14 Partition of damage of RC columns under blast loading

3 结 语

本文通过有限元精细化模拟模型计算爆炸作用下RC柱的损伤值，以此作为BP神经网络的训练样本，结合遗传算法和粒子群算法对网络的初始权值和阈值进行优化，建立了爆炸作用下RC柱的损伤快速评估模型，并验证了其准确性；使用该模型得到了特定RC柱炸药m-Z空间的损伤分布图，可以有效并直观地用于爆炸风险评估并确定结构安全防护距离SD.

参考文献：

［1］ Biggs J M. Introduction to Structural Dynamics[M]. McGraw-Hill College，1964.

［2］ El-Dakhakhni W W，Mekky W F，Rezaei S C. Validity of SDOF models for analyzing two-way reinforced concrete panels under blast loading[J]. Journal of Performance of Constructed Facilities，2009，24(4)：311-325.

［3］ Astarlioglu S，Krauthammer T，Morency D，et al. Behavior of reinforced concrete columns under combined effects of axial and blast-induced transverse loads[J]. Engineering Structures，2013，55：26-34．

［4］ Bao X，Li B. Residual strength of blast damaged reinforced concrete columns[J]. International Journal of Impact Engineering，2010，37(3)：295-308.

［5］ Shi Y C，Hao H，Li Z X. Numerical derivation of pressure-impulse diagrams for prediction of RC column damage to blast loads[J]. International Journal of Impact Engineering，2008，35(11)：1213-1227.

［6］ Flood I，Kartam N. Neural networks in civil engineering(Ⅰ)：Principles and understanding[J]. Journal of Computing in Civil Engineering，1994，8(2)：131-148.

［7］ Flood I，Kartam N. Neural networks in civil engineering(Ⅱ)：Systems and application[J]. Journal of Computing in Civil Engineering，1994，8(2)：149-162.

［8］ Li Z X，Yang X M. Damage identification for beams using ANN based on statistical property of structural responses[J]. Computers & Structures，2008，86(1)：64-71.

［9］ Ibrahim A，Salim H，Flood I. Damage prediction for RC slabs under near-field blasts using artificial neural network[J]. International Journal of Protective Structures，2011，2(3)：315-332.

［10］ Flood I，Bewick B T，Dinan R J，et al. Modeling blast wave propagation using artificial neural network methods[J]. Advanced Engineering Informatics，2009，23(4)：418-423.

［11］ Stewart L K. Testing and Analysis of Structural Steel Columns Subjected to Blast Loads[D]. San Diego：University of California，2010.

［12］ Hagan M T，Demuth H B，Beale M H. Neural Network Design[M]. Boston：Pws Pub，1996.

［13］ Gupta M M，Jin L，Homma N. Static and Dynamic Neural Networks：From Fundamentals to Advanced Theory[M]. New York：John Wiley & Sons，2004.

［14］ Garson G D. Interpreting neural-network connection weights[J]. AI Expert，1991，6(4)：46-51.

(责任编辑：樊素英)

Fast Assessment Model for Damage of RC Columns Under Blast Loading

Li Zhongxian，Zhong Bo，Shi Yanchao
(Key Laboratory of Coast Civil Structure Safety of Ministry of Education(Tianjin University)，Tianjin 300072，China)

A fast assessment model for damage of RC columns under blast loading is proposed based on BP neural networks，by defining 7 structural parameters and 2 loading parameters as input，damage values as output. In the model，the network is trained using 1,032 groups of damage values of RC columns obtained from refined finite element simulation，and the initial weights and bias are optimized by genetic algorithm and particle swarm optimization. The predictive ability of the model is verified by 216 new samples of damage. The research indicates that the developed model can be used for the fast assessment of damage of RC columns under blast loading with reasonable accuracy，and the generated partition figure of damage can be effectively and intuitively used for the blasting risk assessment of RC columns.

blast loading；RC column；damage assessment；risk assessment；BP neural networks

TU375.3

A

0493-2137(2014)11-0973-06

10.11784/tdxbz201310018

2013-10-09；

2013-12-18．

国家科技支撑计划资助项目(2012BAJ07B05)；国家自然科学基金资助项目(51238007，51021004，51008209)．作者简介：李忠献（1961— ），男，博士，长江学者特聘教授，zxli@tju.edu.cn.

师燕超，yanchaoshi@tju.edu.cn.