关于等价无穷小代换求极限的补充说明

沈 燕

(嘉兴学院 平湖校区,浙江嘉兴314200)

函数极限是高等数学的一个重要内容,利用等价无穷小代换求极限是高等数学中求极限的一个重要方法,恰当地使用等价无穷小代换求极限,可化繁为简,变难为易.但对一个分式如果随意利用等价无穷小代换求极限,则很容易出错.在对此问题进行探讨时,有人以定理形式给出对一个分式利用等价无穷小代换求极限的适用范围,但却缺少对一个分式为什么不能随意利用等价无穷小代换求极限进行分析说明.[1]对学习高等数学的学生来说,也是一知半解地照搬那些定理,知其然不知其所以然,造成学习的一大缺憾.笔者拟对此做一些分析与说明.

为叙述方便先给出下面的定义和定理：

定义：设α和β在自变量的同一变化过程中均为无穷小,即：li mα=0,li mβ=0.若li m=c≠0(c为常数),则称α与β是同阶无穷小.特别地,当c=1时,即li m=1,则称α与β是等价无穷小,记作：α～β.

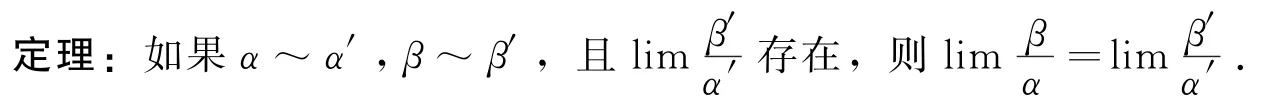
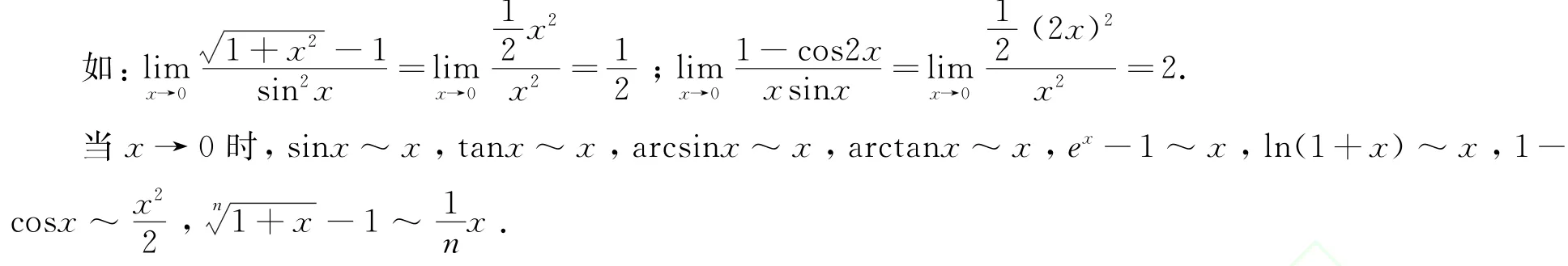
许多书上指出：等价无穷小代换是对分子分母的整体替换 (或对分子分母的因式进行替换),不能对 “+”“-”号连接的各部分分别替换.[2]如：

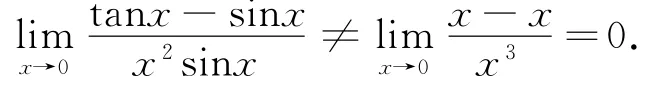
但上题若把分子化成积的形式,就可用无穷小等价代换计算：

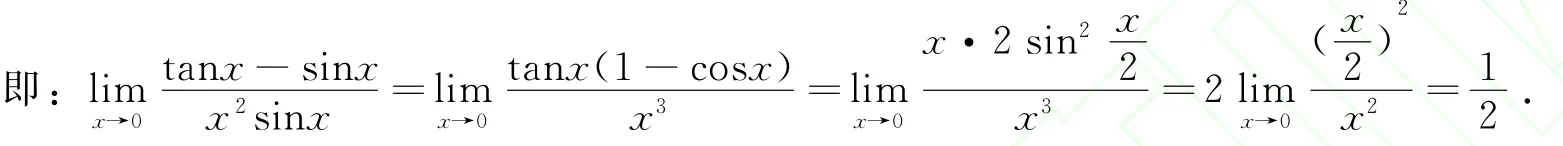
细辨 “不能对 ‘+’‘-’号连接的各部分分别替换”就会发现这是一个假命题,反例如下：

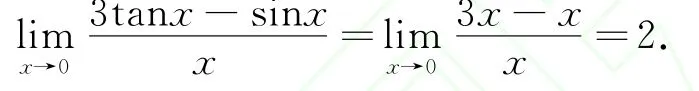
即：有些函数的极限,分子或分母各项用 “+”“-”号连接的各部分仍然可以用等价无穷小去代换.究其原因,可以从极限的运算法则去说明：

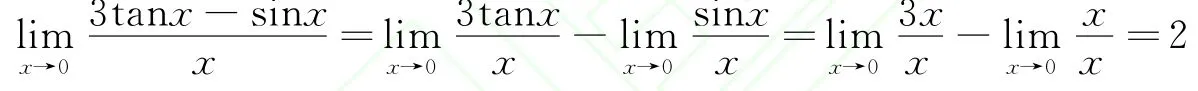
何种情况下等价无穷小代换能对 “+”“-”号连接的各部分分别替换,引起了数学老师对这部分教学内容的探究,如刘静等在 《关于等价无穷小代换求极限方法的一点补充》一文中,对非乘积因子进行等价无穷小的代换方法,以命题形式给出：[3]

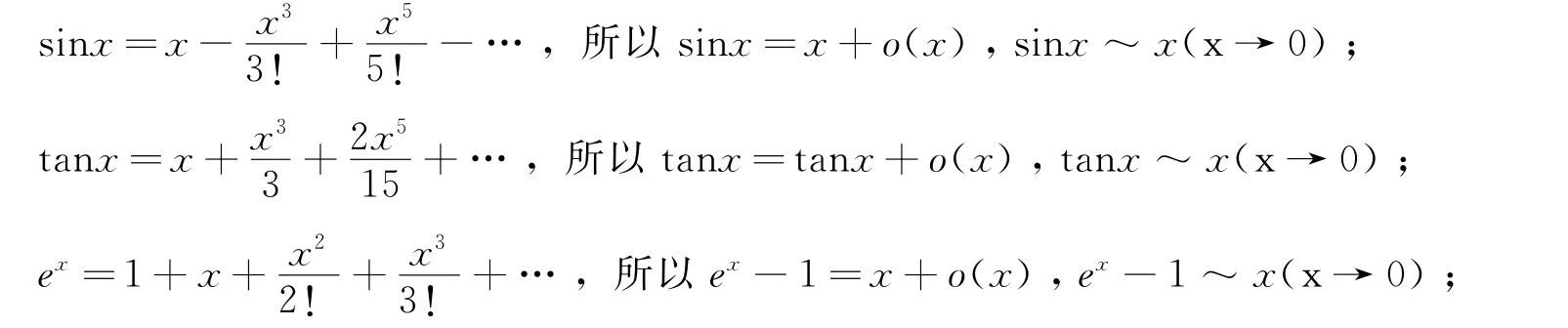
这与把分子化成积的形式后,各因式再用无穷小等价代换的计算结果一致.

总之,等价无穷小代换是对分子分母的整体替换 (或对分子分母的因式进行替换),对 “+”“-”号连接的各部分根据具体情况也可分别替换.

1)求一个分式的极限,当分式中分子、分母中的和或差项只要都是xα(α为常数)的同阶无穷小,则分式中分子、分母的各项都可用等价无穷小直接代换.如：

2)求一个分式的极限,当分式中分子的和或差项是xα(α为常数)的高阶无穷小,分母的和或差项是xα(α为常数)的同阶无穷小,则其值为0;相反,当一个分式中分母的和或差项是xα(α为常数)的高阶无穷小,分子的和或差项是xα(α为常数)的同阶无穷小,则其值为∞;如：

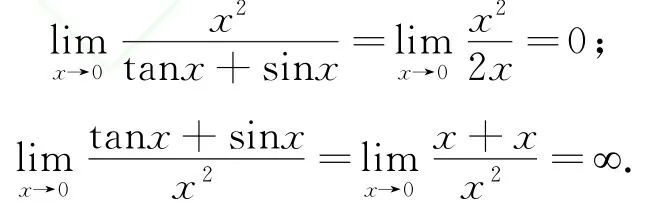
3)求一个分式的极限,当分子、分母中的和或差项同是xα(α为常数)的高阶无穷小,则用其他方法去求极限,如洛必达法则或泰勒展开公式,或先化分子、分母为积的形式,等等.

解法一：

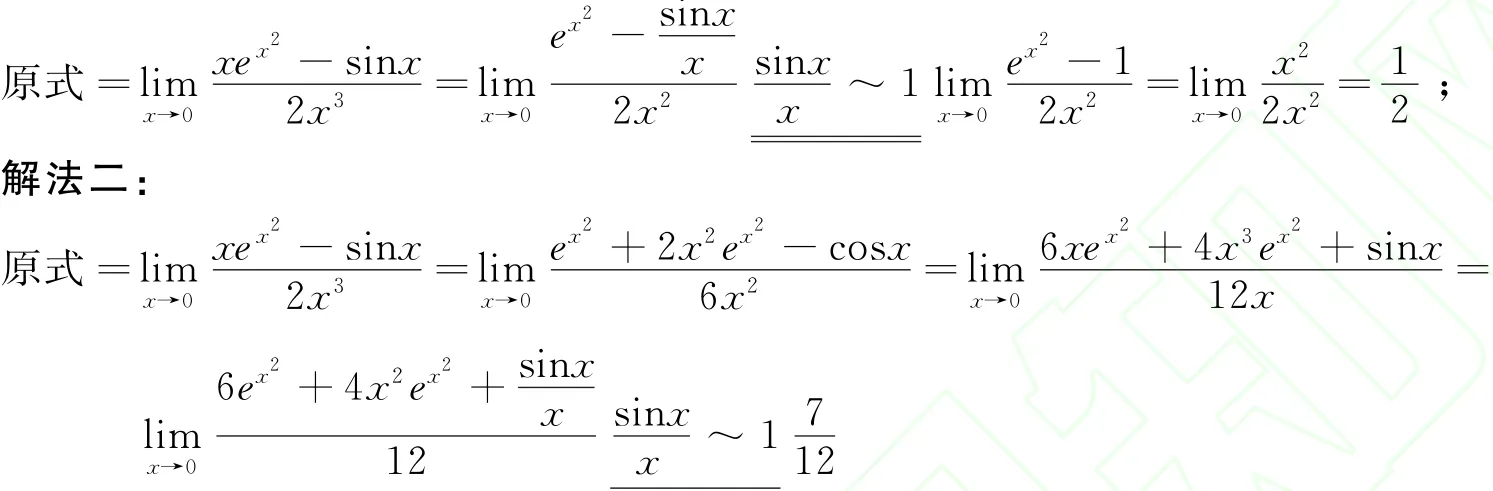
同一题得到两个不同的结果,至少有一个答案是错的,问题出在解法一.

[1]殷君芳.用等价无穷小代换求极限的误区及一点补充 [J].宜春学院学报,2011(4)：25-26.

[2]吴素敏.经济数学 [M].北京：高等教育出版社,2008：24.

[3]刘静,峥嵘.关于等价无穷小代换求极限方法的一点补充 [J].嘉兴学院学报,2005(5)：23-25.