风帽结构设计优化模型的建立

李 哲

(嘉兴学院设计学院,浙江嘉兴314001)

风帽结构设计优化模型的建立

李 哲

(嘉兴学院设计学院,浙江嘉兴314001)

通过测量头部和颈部在各种活动状态下各部位的尺寸,分析出符合头部、颈部活动变化需求的风帽各结构(如帽长、帽宽)的参数.根据参数绘制出两片型风帽结构,经过与人体数据的比较分析得出,两片型风帽在合体性和美观性上都有所欠缺,而分割型风帽则比较合体.同时,通过SPSS软件的多元线性回归分析得出分割型风帽小片量与头围长及帽长的数学模型,进而以人体头围长及帽长的尺寸得到最优化的分割型风帽.

分割型风帽;结构;优化设计;活动尺度

风帽,也叫连衣帽,是一种典型的罩帽,将整个头部包裹,仅露出脸部,常见与上衣相连,成为服装的领帽部分.[1]风帽同其他类型的帽子一样,都具有遮阳、遮雨、防风、保暖、安全及审美装饰等主要功能.[2-3]不同于其他帽子的是它直接与衣身相连,不仅充当一种服饰配件,也是服装上衣不可或缺的重要组成部分.因此,风帽的结构设计比一般的帽子更加复杂,所要考虑的因素更多,帽型结构的变化也更加丰富.在设计风帽结构时不仅要将人体头部的结构特征考虑进去,还要把人体头颈部的运动形态作为一个重要的参考因素,[4-5]而时下的风帽结构设计往往没有完全考虑到这些因素,使得风帽在功能性及合体性上都还不尽如人意,研究风帽结构优化可以改善风帽的服用性能,有一定的市场应用价值.

1 头颈部数据测量

影响风帽结构的因素主要包括人体的头围和头长,人体头长指的是从头顶点至侧颈点的弧线长度.人体的头围长决定了风帽的帽宽取值,而人体头长是影响帽长取值的重要因素.人体的头部及颈部在做向上伸长或向左向右倾斜时,从头顶点至侧颈点的弧线长度将会发生变化,使得帽长成为了一个变量,可见人体头颈部的运动形态也是设计风帽结构时不可忽视的一个重要因素.如果只考虑头颈部正常静态状态下各部位的尺寸来制作风帽,这样得到的风帽显然不能满足人体头部的活动需求,不符合对其合体性及科学性的要求.

本文以10名20~25岁年龄段的大学生为研究对象,相关的人体头颈部尺寸及测量方法如下:[6]

1)头围长——经头部眉间点、头后突点围量一周得到;

2)静态帽中弧长——头颈部呈正常直立状态下,从前额到后颈点的最短曲线长度;

3)动态帽中弧长——颈部向前屈至最大角度时,从前额到后颈点的最短曲线长度;

4)静态头长——头颈部呈正常直立状态下,从头顶点到侧颈点的最短曲线长度;

5)动态头长——颈部向左(或向右)做最大侧屈时,从头顶点向右(或向左)到侧颈点的最短曲线长度;

6)静态头高——头颈部呈正常直立状态下,下颌点到头顶点的垂直距离;

7)动态头高——颈部向上直立伸长至最大程度时,测量下颌点到头顶点的垂直距离.

以上各部位尺寸的测量数据如表1所示.

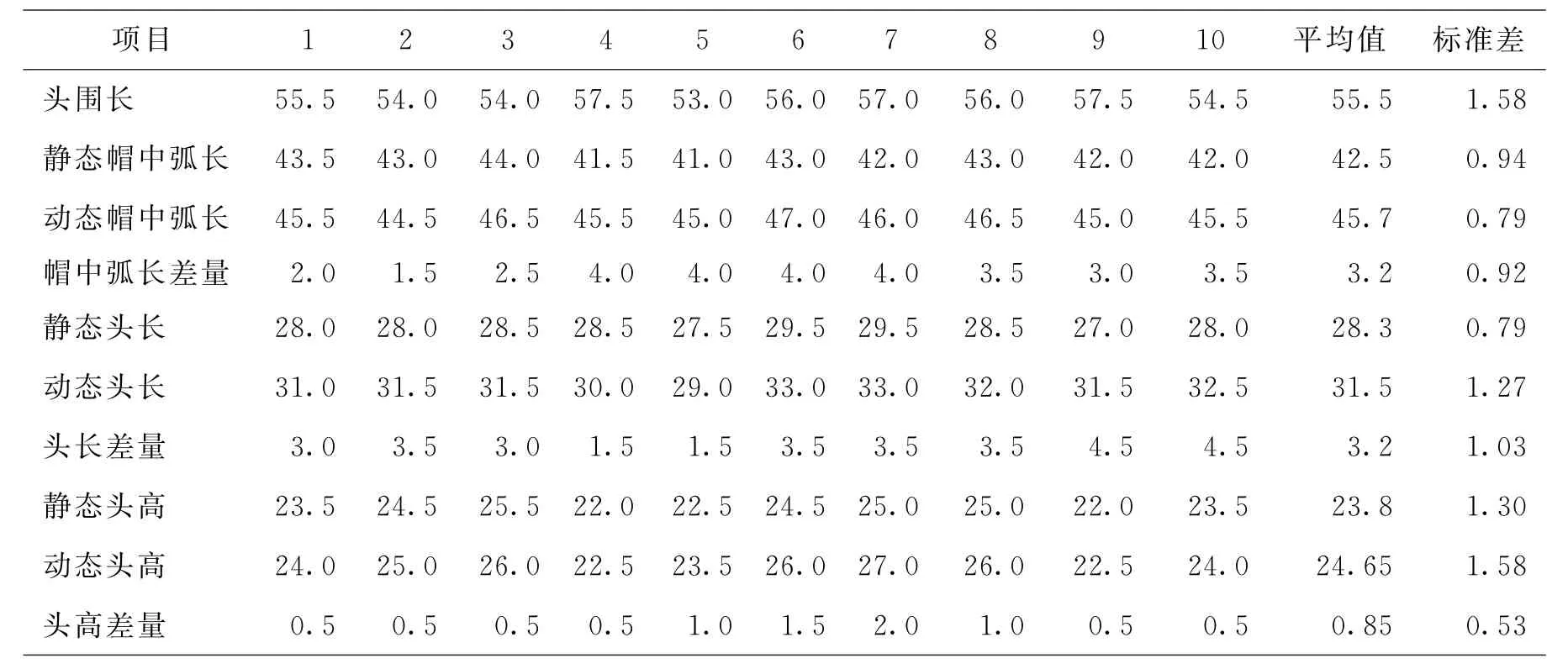
表1 头颈部各部位测量数据 cm

从表1中我们可以看出,动态与静态相比,头高的增加量比头长的增加量明显要小,因此,可以将动态头长作为确定帽长参数的主要参考因素来分析,而帽宽则是根据头围长来确定.

2 两片型风帽的结构设计

两片型的风帽结构比较简单,因此其结构制图方法的运用比较普遍,一般的两片型风帽的制图方法是:先将后衣身在前衣身肩线的延长线上拼合.在后颈点BNP下部取2nb定为帽座,帽座量一般取0~3 cm,画顺帽下口线,使A~BNP＝A’~BNP’.帽下口线向外延长3 cm画垂线,在垂线上取动态头长作为帽长,再画帽长线的垂线,在垂线上取帽宽＝头围的1/2.在帽后顶部各取边长13 cm画圆弧形帽顶,并将帽前部下落2~3 cm,画顺造型.[7]如图1所示.

然而,仅仅依靠合理的帽长及帽宽并不能够设计出完全合体的风帽.可运用CAD软件,在上述的两片型风帽结构制图方法的基础上,根据实际测得的各帽宽及帽长数据,绘制出对应的风帽结构,然后通过CAD软件中的测量长度工具测量出帽中弧长的长度,[8]将得到的数据与实际人体上测得的颈部向前屈至最大角度时,从前额到后颈点的最短曲线长度进行比较(见表2),可以看出,通过上述的两片型风帽结构制图方法所得到的风帽对人体头部来说过于宽松,这样的风帽结构在合体性和美观性上都有所欠缺.因此,要在合理的帽长及帽宽数据的基础上对两片型风帽的结构加以改进,以得到更合体的风帽结构.

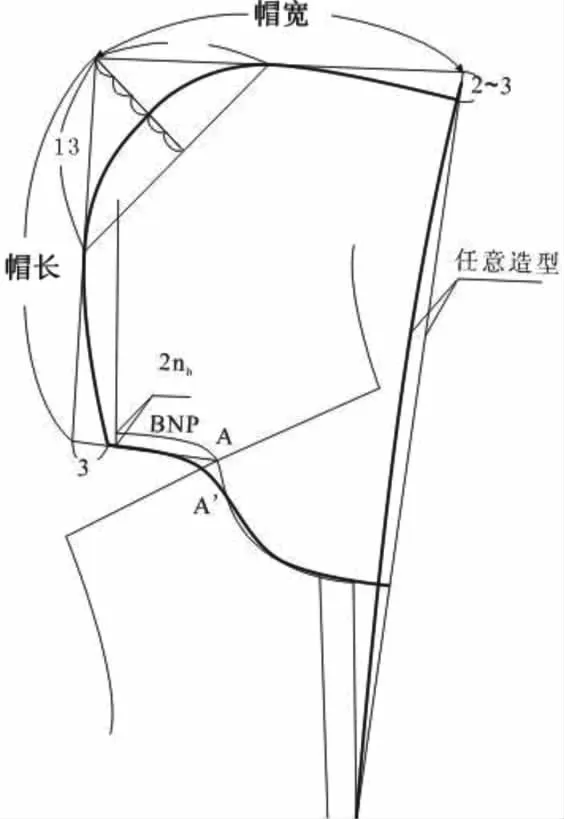
图1 两片型风帽的结构制图

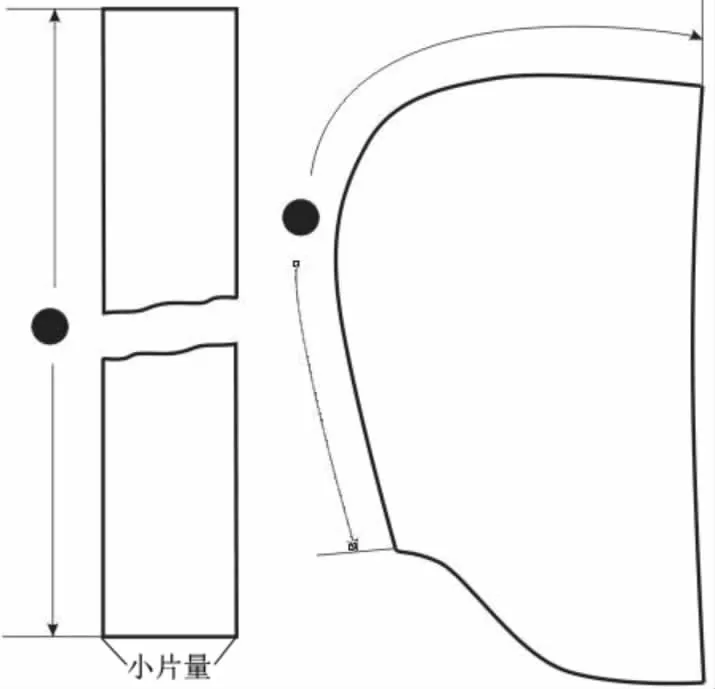
图2 分割型风帽的结构制图

3 风帽的结构设计优化

为了使风帽更符合人体的头部形态,可以将帽中弧长上多余的量通过收省的方式从帽中弧长上减掉.对于这8 cm左右的省道量,可以将其分成3个小量的省道在风帽结构的不同位置来进行收省,但是由于省道太多,影响帽子的美观性,故可以采用分割型的风帽结构.

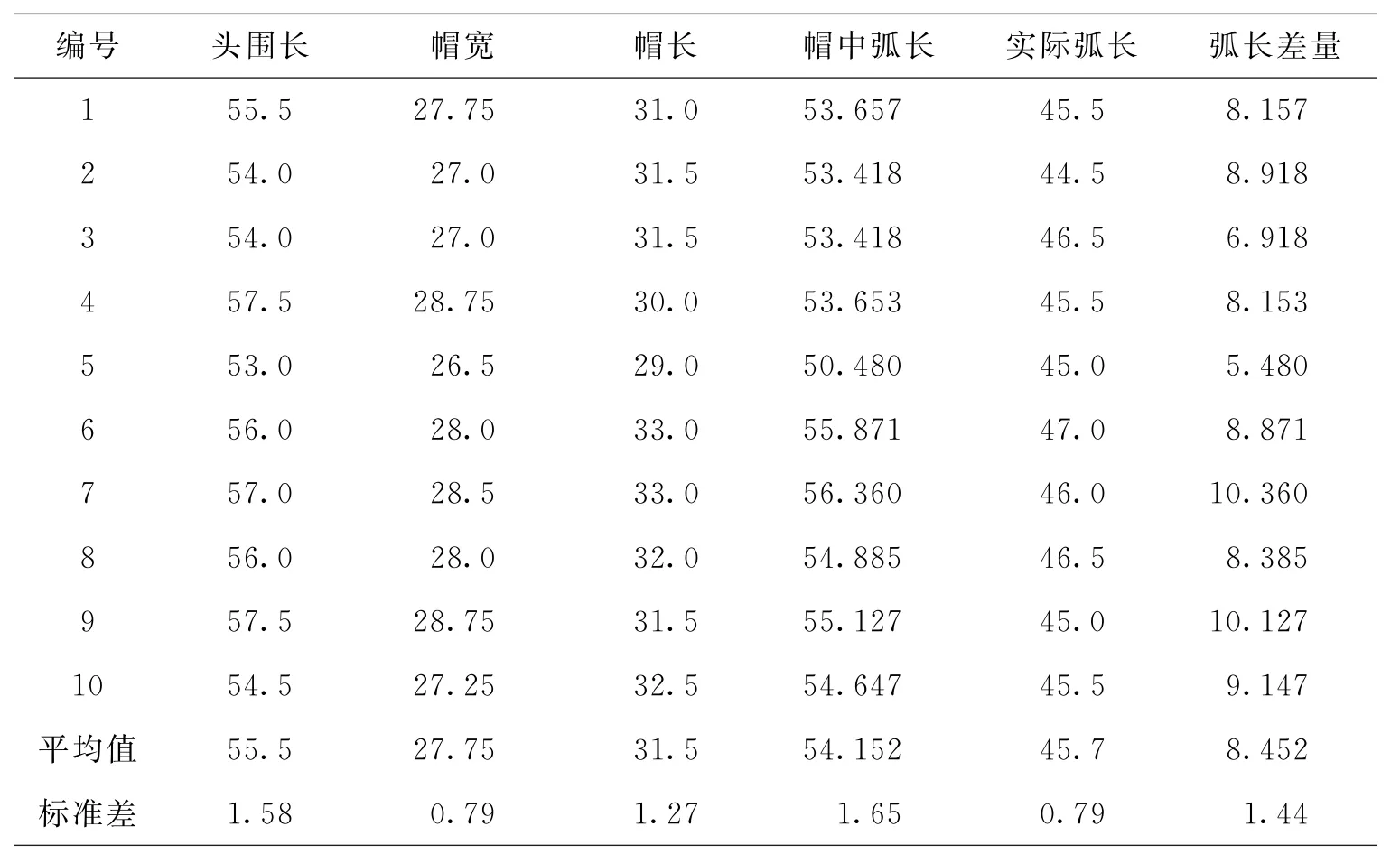
表2 两片型风帽帽中弧线长与实际弧长的比较 cm

3.1 分割型风帽的结构设计

分割型风帽也是在两片型风帽结构的基础上进行制图的,具体的方法是从两片型风帽的帽顶边缘分割出一个小片制作成左右相连的帽条,并且是用直料裁制,剩下的帽身在下口线处去除一定的省道量,使帽身符合人体头部的形态,并且与领窝弧线等长,如图2所示.

3.2 分割型风帽的参数确定

分割型风帽的结构制图并不难,主要是要确定好中间分割出的小片宽的大小(小片量),我们可以利用小片的长度与分割后剩下的帽身的上沿弧线的长度相等,并与头部向前屈至最大角度时所需前额到后颈点的曲线长度相符合这一点来确定其宽的大小.具体的方法是通过依次设定不同数值的小片量,在两片型风帽结构的基础上利用CAD软件绘制出对应的帽身,并用软件中的测量长度工具测量相应的帽身上沿弧线的长度,将其与实际测得的颈部向前屈至最大角度时,从前额到后颈点的最短曲线长度进行比较,得出最合适的小片量,测得的数据如表3所示.

表3 不同头围长及帽长对应的小片量 cm

使用SPSS统计软件的多元线性回归分析功能对上面这些数据进行综合分析,采用向前选择法,先将最大相关的变量进入模型,如果通过F检验,则在剩余的变量中寻找具有最大偏相关系数的变量,直到将所有符合条件的自变量全部加入到模型中.[9-10]最后得到如表4的输出结果,可以看出,其T统计量对应的显著性水平都小于0.05,说明这个多元回归模型是有意义的.

表4 多元回归模型的回归系数表

根据表4中的数据可得出小片量与头围长及帽长的数学模型为:Y＝0.535X1+0.9X2-47.379 (Y是小片量,X1是头围长,X2是帽长).

3.3 小片量数学模型的验证

通过选定研究对象来制作分割型风帽,测得头围长为57 cm,帽长为34 cm,根据上面得到的小片量与头围长及帽长的数学模型可以计算出其所需小片量的大小为13.716 cm.利用CAD软件根据头围长和帽长的数值,在小片量确定为13.716 cm的前提下,在两片型风帽结构的基础上绘制出对应的分割型风帽,再制作出实物,如图3所示.可见这款分割型风帽无论是在合体性还是外观上都非常符合我们对合理性风帽的要求,而且能满足人体头部的动态需求,因此,用小片量数学模型所得的分割型风帽是最优化的风帽结构设计.

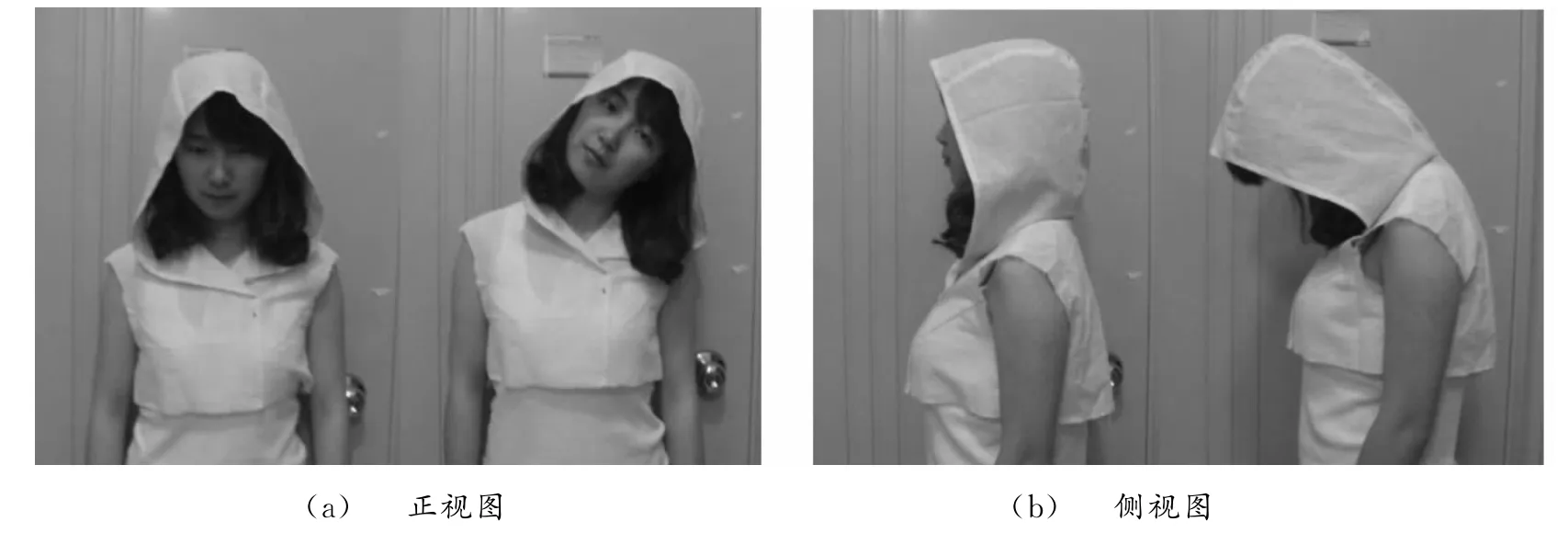
图3 分割型风帽成品展示

4 结论

通过对人体头部及颈部在静态和动态状态下各部位数据的测量,分析出决定风帽结构的帽长、帽宽参数,并结合原有的两片型风帽结构制图方法加以分析,得出分割型风帽是更合体的风帽结构.

分割型风帽是在两片型风帽的结构基础上制图而成的.其中风帽中间的小片量对分割型风帽结构的确定有着重要的作用.本文利用SPSS统计软件的多元线性回归分析功能可得出一个小片量与头围长及帽长的数学模型:Z＝0.535X+0.9Y-47.379(Z是小片量,X是头围长,Y是帽长),由此小片量的大小就可以通过较易测得的头围长及帽长数据得到.通过这种方法制作的分割型风帽科学、合理,是最优化的风帽结构.

[1]吴厚林.帽子结构设计研究[J].西安工程科技学院学报,2006,20(3):280-283.

[2]邓洪涛,李哲.平顶休闲帽的制图与裁剪[J].嘉兴学院学报,2002,14(6):71-73.

[3]马蓉.服饰品设计[M].北京:中国轻工业出版社,2001:7-10.

[4]刘瑞璞.服装纸样设计原理与应用[M].北京:中国纺织出版社,2008:34.

[5]王秀芝,徐静,李敬华.基于颈部运动特征的立领造型研究[J].山东纺织经济,2006(2):44-45.

[6]顾韵芬.服装结构设计与制推板技术[M].沈阳:辽宁美术出版社,2002:44.

[7]张文斌.服装结构设计[M].北京:中国纺织出版社,2007:184-185.

[8]李哲.服装CAD技术运用[M].北京:中国轻工业出版社,2010:172.

[9]朱建平,殷瑞飞.SPSS在统计分析中的应用[M].北京:清华大学出版社,2007:113.

[10]尹海洁,刘耳.社会统计软件SPSS for Windows简明教程[M].北京:社会科学文献出版社,2003:110.

(责任编辑 张争)

Optimized Design of Hood Structure

Li Zhe
(College of Design,Jiaxing University,Jiaxing,Zhejiang314001)

This research is to optimize the hood structure through measurement the sizes of the head and neck at all kinds of activity state,getting the parameters of the structure of hood,such as the length and the width of hood,which accord with the movement of the head and neck.According to the parameters and by comparison and analysis with human body data,it can be drawn the two-piece hood is not good in fitness and aesthetics and three-piece hood is more fitted structure.A mathematical model about the relationship between the width of the middle piece with the head circumference and hood length can be got with the multiple linear regression in SPSS,so that the optimal three-piece hood can be got just with head circumference and hood length.The result shows that the three-piece hood made by this method is the optimal hood structure.

Hood;Structure;Optimal design;Activity scale

TS941.72

A.

1671-3079(2014)03-0120-05

10.3969 /i.issn.1671-3079.2014.03.023

2013-11-17

李哲(1971- ),女,浙江金华人,嘉兴学院设计学院讲师,硕士,主要研究领域包括服装的舒适性、服装结构设计、服装CAD等.

时间:2014-04-02 11:07 网络出版地址:http://www.cnki.net/kcms/detail/33.1273.Z.20140402.1107.008.html