基于知识板的协同粒子滤波算法

王雁鹏，王 磊，邹 锋，钱新桥



基于知识板的协同粒子滤波算法

王雁鹏，王 磊，邹 锋，钱新桥

(西安理工大学计算机科学与工程学院，西安 710048)

在当前的粒子滤波中，粒子可能出现退化现象和重采样，导致样本枯竭从而破坏粒子多样性。针对该问题，借鉴知识板和协同进化理论，提出一种基于知识板的协同粒子滤波算法。该算法对重要性密度函数进行采样，形成采样粒子样本，并将粒子划分为若干个子采样粒子群，对每个子采样粒子群在不同的区域进行搜索，通过子采样粒子群之间的通信，最终找到动态系统的最佳状态估计。理论分析与仿真结果表明，该算法能提高经典粒子滤波算法的群体多样性，在加快收敛速度和降低计算复杂度方面有较大优势。

粒子滤波；多样性；知识板；协同；采样；优化

1 概述

20世纪60年代末自动控制领域引入粒子滤波(Particle Filtering, PF)方法并在70年代得到发展[1-2]。PF是基于Monte Carlo方法和Bayes估计理论，但粒子滤波有粒子退化现象[3]。1993年，Gordon等人提出自举粒子滤波(bootstrap particle filtering)算法，该算法引入重新采样的思想[4]。

粒子滤波技术在非线性[5]、非高斯系统表现出来的优越性，决定了它的应用范围非常广泛。另外粒子滤波器[6]的多模态处理能力，是它应用广泛的原因之一。国际上粒子滤波已被应用于各个领域。在经济学领域它被应用在经济数据预测；在交通管制领域它被应用在对车或人视频监控；另外，它还用于机器人的全局定位、协同跟踪等领域[7]。

粒子滤波由于采用了重新采样的思想，能够在一定程度上缓和粒子退化的加剧及无效粒子的增加，但是又会产生一个新的问题，也就是样本枯竭问题：随着算法迭代的进行，样本只是那些拥有较大权重的粒子经过反复复制后的后代，而拥有较小权重的粒子被丢弃，导致采样样本中有着大量的相同粒子，致使粒子多样性丢失。

本文提出一种免重采样的基于知识板的协同粒子滤波算法(Knowledge-based Cooperative Particle Filter, KCPF)，以期保证粒子多样性，并且从某种程度上抑制粒子退化现象，最终提高算法在状态估计中的性能。

2 基于知识板的协同粒子滤波算法设计

2.1 粒子滤波算法

粒子滤波[8-9]基于Monte Carlo[10]思想和递归Bayes估计，是利用Monte Carlo方法求解Bayes估计中的积分。粒子滤波的核心思想是：根据动态系统状态向量的经验条件分布，在动态系统状态空间产生一组随机样本集合，这些样本称为粒子；依据观测的结果不断调节粒子的位置和权重；根据调节后的粒子信息修正原先的经验条件分布。

粒子滤波算法过程描述如下：

Step2更新。更新粒子的权值：

Step3重采样。

2.2 KCPSO算法

KCPSO[11]基于知识板和协同进化理论。知识板的局部知识集和全局知识集都是使用一个五元集合来表示，包括子群体或是整个群体的多样性、搜索能力、生存状态、最优系统状态、重要性权值信息。

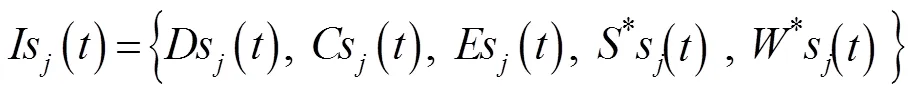
子群体多样性可以使用采样粒子相对于当前子采样粒子群平均粒子位置的平均值来计算。而群体多样性的计算可以使用各个子群体的最优系统状态估计相对于当前所有子群体的平均最优系统状态估计的平均值来计算。

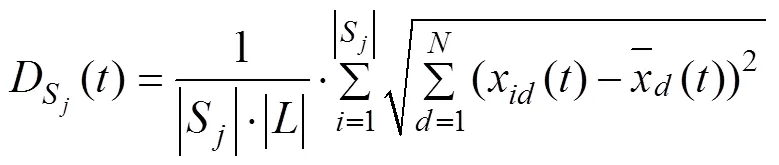
Cs()是用来评价群体的搜索能力的，具体定义如下：

显然，Cs()的值越大，该子群体的搜索能力越强，反之越弱。同样，C()的值越大，整个群体的搜索能力越强，反之越弱。

Es()和E()描述的子群体和整个群体的生存状态。 3个生存状态分别定义为：

在对动态系统进行状态估计时，每个采样子粒子群都有它自己的生命周期，从初始化开始(对重要密度函数进行采样，并对采样粒子群粒子赋上初值)，经过成长，到成熟收敛，整个过程中的不同信息将不断被抽取用于知识板上局部知识的更新。

在子粒子群或整体粒子群处于成长状态，则在进行局部搜索过程中，粒子的信息更新可以根据下式进行：

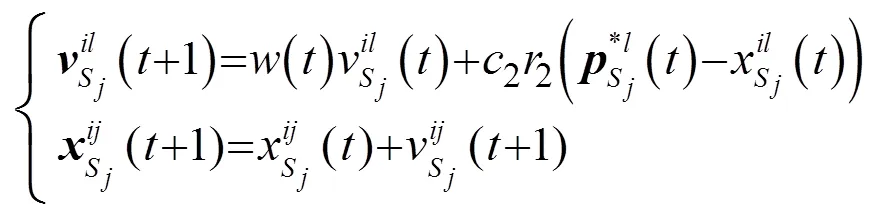
当任一子粒子群体处于伪成熟状态时为协同行为，粒子的位置和速度更新方程如下：

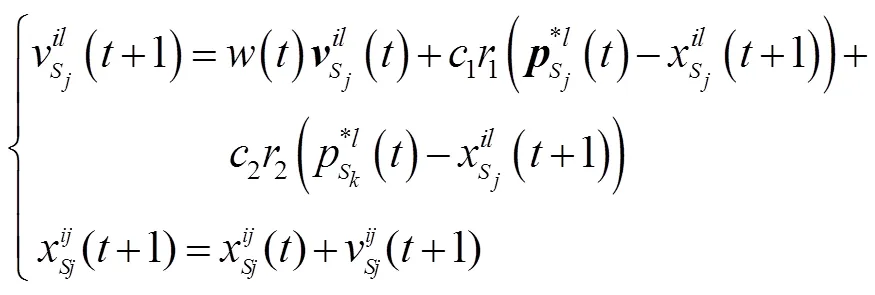
2.3 KCPF算法

KCPF核心思想：对重要性密度函数进行采样形成采样粒子样本并对粒子样本划分若干个子采样粒子群，每个子采样粒子群在不同的局部区域进行搜索，并通过子采样粒子群之间的通信，最终找到动态系统的最佳状态估计。这样做有2个好处：有利于维持种群搜索过程中的多样性，防止粒子退化现象；可通过众多局部极值点的搜索信息来引导对全局极值点的搜索，从而增加算法全局收敛的概率。

对系统进行状态估计时，首先在采样过程中引入最新的观测值，定义适应度函数：

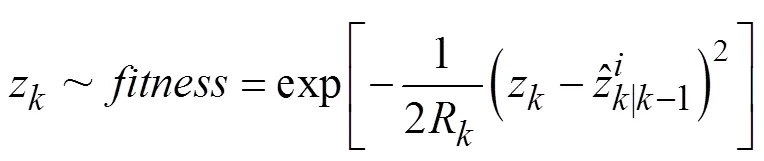
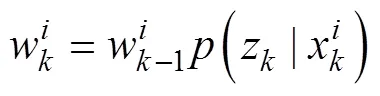
观测值计算由式(8)获得，算法具体步骤描述如下：

Step1 采样粒子并初始化。

Step2计算重要性权值。

Step3根据最优值更新采样粒子，使采样粒子不断的向真实状态靠近。

Step3.1 如果满足终止条件(重要性权值是否符合预设的阈值)，则转到Step4；否则，转到步骤Step3.2。

Step3.2如果任一子采样粒子群体的生存状态为成长状态，则子采样粒子群体按式(6)更新采样粒子的速度和位置，否则转到步骤Step3.3。

Step3.3 如果任一子采样粒子群体的生存状态为伪成熟状态，则子采样粒子群体按式(7)更新采样粒子的速度和位置；否则，转到步骤Step3.4。

Step3.4 如果任一子采样粒子群体的生存状态为成熟状态，则对子采样粒子群中任一采样粒子进行重新初始化，并计算重要性权值。

Step3.5 计算每一个子采样粒子群体中的采样粒子适应值(重要性权值)，统计分析每一个子采样粒子群体的多样性、搜索能力、生存状态等，更新知识板上的知识元素，转到步骤Step3.1。

Step6如果符合结束条件，则退出算法，否则，继续Step1。

KCPF算法流程描述如图1所示。

图1 KCPF算法流程

3 仿真实验与结果分析

3.1 控制系统状态跟踪实验

假设系统模型如下：

状态方程：

观测方程为：

在仿真实验中，设定后验概率密度分布中2.5%~97.5%的间隔范围为置信度95%的置信区间，高置信水平的代价是宽的置信区间，通过保证置信区间中最有效的包含目标状态的真实值而使目标估计具有最小的误差。分别对EKF滤波算法、KCPF算法的置信区间进行分析，其中KCPF算法的采样粒子数为2 000。仿真结果如图2、图3所示。

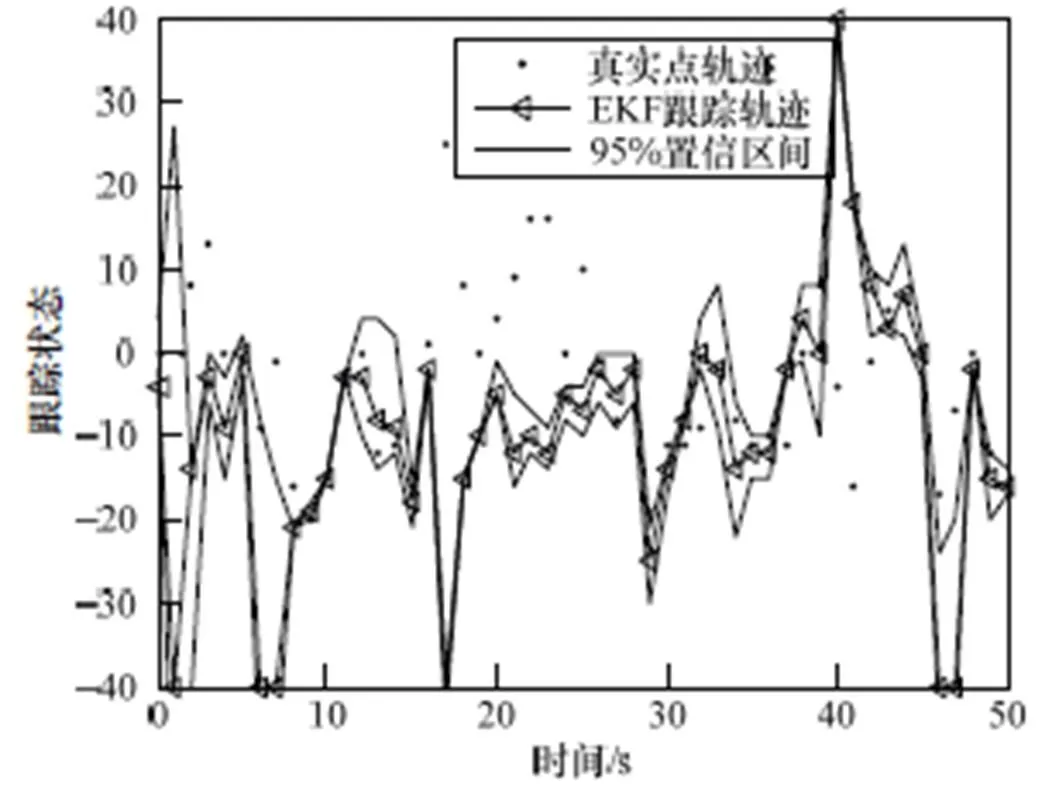
图2 EKF的置信区间分析

图3 KCPF的置信区间分析

通过图2、图3分析可以得知：EKF算法的置信区间最小，很明显KCPF的置信区间是最大的，这也说明KCPF算法的效果要比较好，这是由于KCPF算法通过将采样粒子样本分解成若干子粒子样本，增加了采样粒子的多样性，从而扩大了估计的置信区间，在置信区间中更好的包含了状态的真实值的同时也使跟踪的准确性有所增加。

3.2 转弯模型状态跟踪实验

假设机动目标的运动模型是协同转弯模型，并假设空间维数是二维。假设目标的初始位置为：=[–2 000 m,0]，初始速度为：=300+(为[0,1]之间的随机数)，仿真实验的时间长度为：180 s，在第0~66 s处做匀速直线运动，在第67 s~85 s处做圆周运动，在第86 s~180 s处重新做匀速直线运动，转弯处的加速度为50。采样粒子3 000。

使用KCPF算法和EKF滤波算法跟踪机动目标的轨迹及轴和轴方向的误差如图4~图6所示。通过对比可以知道，EKF算法在机动目标跟踪系统的运动模型和协同转弯模型的时候，跟踪误差要比KCPF算法在机动目标跟踪中的跟踪误差要大很多。因为大多数目标跟踪系统是以协同转弯模型为运动模型的，所以KCPF在目标跟踪中具有比较好的应用。基于转弯模型状态跟踪仿真实验也说明了KCPF算法在目标跟踪中应用的有效性。

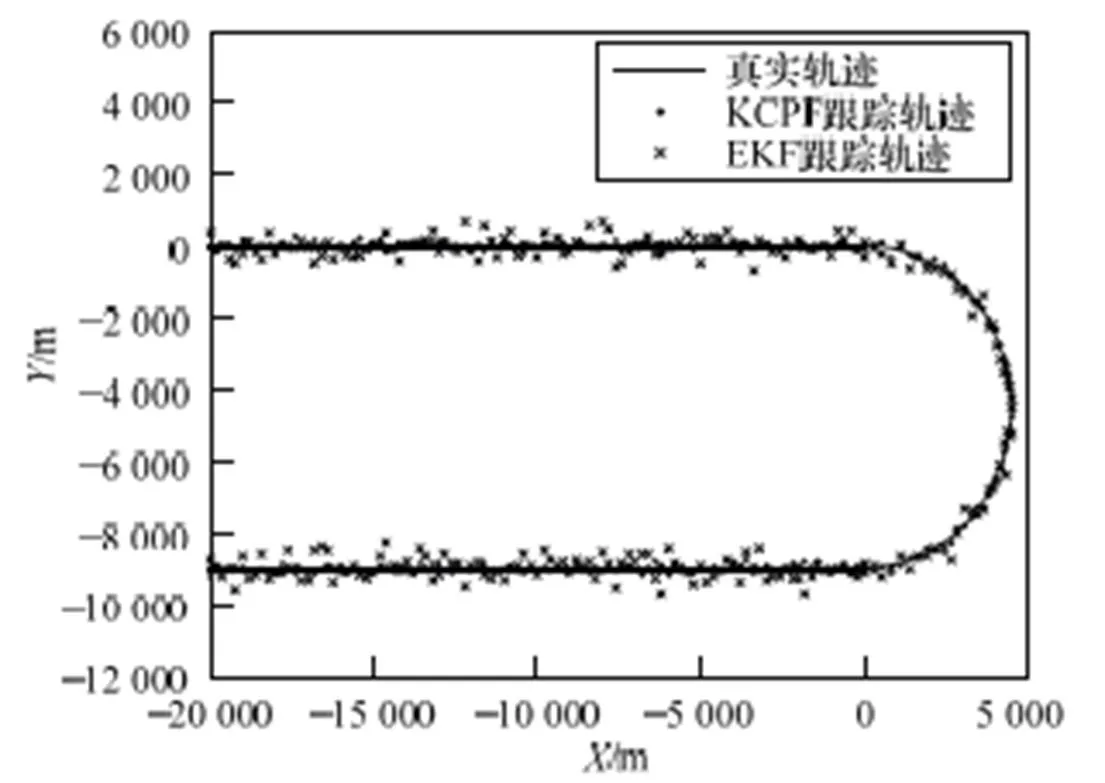
图4 KCPF和EKF的跟踪轨迹

图5 KCPF的跟踪误差

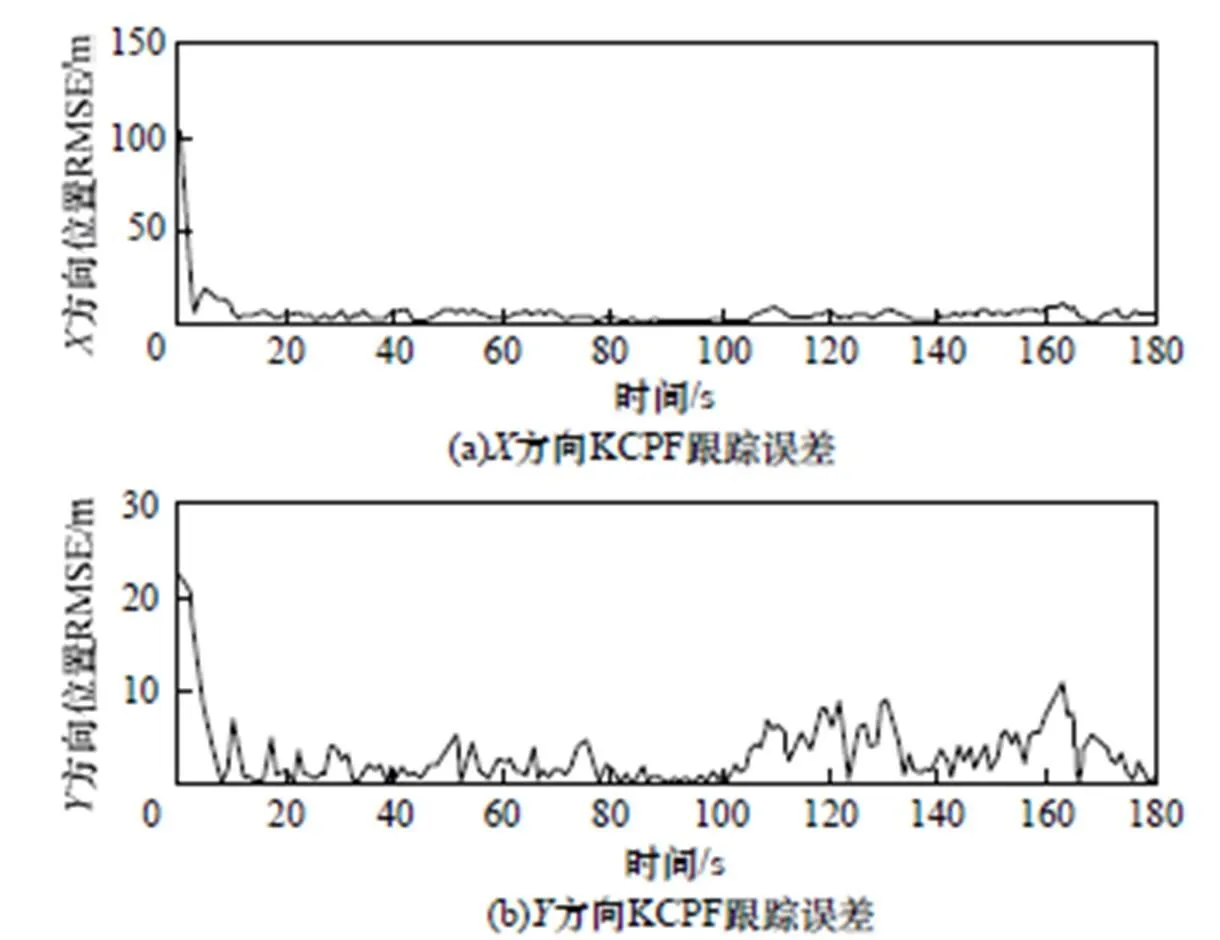
图6 EKF的跟踪误差

4 结束语

本文提出的KCPF算法借鉴KCPSO算法中基于知识板的协同理论，通过将采样粒子群分为若干个子粒子群，各个子采样粒子群在各自的解空间中进行寻优，同时通过知识板的通信，在算法的运行过程中，保证采样粒子的多样性。另外由于KCPF算法是免重采样的，解决了由重采样带来的样本枯竭问题。基于控制系统状态跟踪和转弯模型状态跟踪的仿真实验结果表明KCPF算法达到了优化[12]粒子滤波的目的。

[1] Handschin J E, Mayne D Q. Monte Carlo Techniques to Estimate the Conditional Expectation in Multi-stage Non-linear Filtering[J]. International Journal of Control, 1969, 9(5): 547-559.

[2] Zaritsky V S, Svetnik V B, Shimelevich L I. Monte Carlo Techniques in Problems of Optimal Information Processing[J]. Automation and Remote Control, 1975, 36(3): 2015-2022.

[3] Godsill S, Clapp T. Improvement Strategies for Monte Carlo Particle Filters[J]. Signal Processing, 1998, 2(1): 17-23.

[4] Gordon N J, Salmond D J, Smith A F M. Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation[J]. Radar and Signal Processing, 1993, 140(2): 107-113.

[5] Carpenter J, Clifford P, Fearnhead R. Improved Particle Filter for Nonlinear Problems[J]. IEE Proceedings Radar, Sonar and Navigation, 1999, 146(1): 2-7.

[6] Nummiaro K, Koller-Meier E, van Gool L, et al. An Adaptive Color-based Particle Filter[J]. Image and Vision Computing, 2003, 21(1): 99-110.

[7] Hue C, Cadre J, Perez P. Tracking Multiple Objects with Particle Filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 791-812.

[8] Doucet A, de Freitas N, Gordon N. An Introduction to Sequential Monte Carlo Methods. Sequential Monte Carlo Methods in Practical[M]. New York, USA: Springer-Verlag, 2001.

[9] Hu Xiaoli, Schon T B, Ljung L. A Basic Convergence Result for Particle Filtering[J]. IEEE Transactions on Signal Processing, 2008, 56(4): 1337-1348.

[10] Crisan D, Doucet A. Convergence of Sequential Monte Carlo Methods[M]. Cambridge, UK: Cambridge University Press, 2000.

[11] Jie Jin, Zeng Jianchao, Han Chongzhao, et al. Knowledge- based Cooperative Particle Swarm Optimization[J]. Applied Mathematics and Computation, 2008, 205(2): 861-873.

[12] Bergh F V D. An Analysis of Particle Swarm Optimizers[D]. Cape Town, South Africa: Department of Computer Science, University of Pretoria, 2002.

编辑 索书志

Cooperative Particle Filtering Algorithm Based on Knowledge Plate

WANG Yan-peng, WANG Lei, ZOU Feng, QIAN Xin-qiao

(School of Computer Science and Engineering, Xi’an University of Technology, Xi’an 710048, China)

For the degeneracy phenomenon of particles caused by evoluting and the impoverishment problem of particles caused by resampling. This paper proposes a novel particle filtering algorithm based on knowledge plate and coevolution. The main idea of this algorithm is to sample from the importance density function and generate particle samples which are divided into several sub-sample groups. Each sub-sample group searches among different area and finds the optimal state estimation of this dynamical system by means of the communication between each other. Theoretical analysis and experimental simulation results show that the proposed algorithm improves population diversity and has potential advantages in convergence rate and computational complexity, thus enhances the searching performance of the algorithm.

particle filtering; diversity; knowledge plate; cooperative; sampling; optimization

1000-3428(2014)03-0228-04

A

TP18

国家自然科学基金资助项目(61073091, 61100173)；陕西省自然科学基金资助项目(2010JM8028)。

王雁鹏(1985－)，男，硕士，主研方向：智能信息处理，系统可靠性分析与设计；王 磊(通讯作者)，教授、博士生导师；邹 锋，讲师、博士；钱新桥，硕士。

2012-09-26

2013-01-12 E-mail：wangleeei@163.com

10.3969/j.issn.1000-3428.2014.03.048