基于混沌多目标粒子群优化算法的云服务选择

王 娜，卫 波，王晋东，张恒巍



基于混沌多目标粒子群优化算法的云服务选择

王 娜，卫 波，王晋东，张恒巍

(解放军信息工程大学密码工程学院，郑州 450001)

随着云计算环境中各种服务数量的急剧增长，如何从功能相同或相似的云服务中选择满足用户需求的服务成为云计算研究中亟待解决的关键问题。为此，建立带服务质量约束的多目标服务组合优化模型，针对传统多目标粒子群优化(MOPSO)算法中解的多样性差、易陷入局部最优等缺点，设计基于混沌多目标粒子群优化(CMOPSO)算法的云服务选择方法。采用信息熵理论来维护非支配解集，以保持解的多样性和分布的均匀性。当种群多样性丢失时，引入混沌扰动机制，以提高种群多样性和算法全局寻优能力，避免陷入局部最优。实验结果表明，与MOPSO算法相比，CMOPSO算法的收敛性和解集多样性均得到改善，能够更好地解决云计算环境下服务动态选择问题。

云计算；服务选择；服务质量；多目标粒子群优化算法；信息熵；混沌

1 概述

云计算[1]是一种新兴的计算模式，它通过将大量的网络资源(计算资源、存储资源与软件资源等)以服务的形式链接在一起，形成巨大规模的共享虚拟资源池，为用户和应用系统提供“能力无限”的云服务资源。在云计算环境中有大量功能相同、非功能属性各异的云服务，而单个云服务的功能有限，因此，如何将云计算环境中多个云服务组合起来形成新的、增值的大粒度组合服务来满足复杂多变的应用需要，是当前迫切需要解决的问题。

服务组合指将现有服务按照一定的业务逻辑进行无缝集成，从而更好地满足用户的需求。服务组合广义上可以分为静态组合、半自动组合和自动组合[2]。云计算环境是一个动态开放的环境，云服务的状态随时可能发生变化，静态的组合无法满足实际的应用需求。同时，由于完全智能的自动组合是一个十分复杂的过程，因此很多关于服务组合的应用和研究工作都侧重于半自动方式[3]。半自动组合的实现，首先由业务人员根据特定的任务需求建立服务组合流程模型。服务组合模型由多个服务节点组合，每个节点有多个功能相同、服务质量(Quality of Service, QoS)不同的候选服务。如何从众多的候选服务中动态地选择合适的服务实例，形成一个QoS全局最优的可执行组合服务来完成用户的需求，成为服务组合中的一个关键问题，本文称其为QoS全局最优动态服务选择。

QoS全局最优动态服务选择问题已被证明为NP完全问题[4]，受到国内外众多学者的关注。文献[5-6]把服务节点的候选服务的QoS属性进行加权排序，然后选择加权和最大的服务实例来完成服务节点的功能，但没有考虑服务节点之间的逻辑关系，属于局部最优的服务选择方法，无法得到QoS全局最优的组合；文献[7-8]虽然引入智能优化算法，但需要把组合服务的各个QoS参数线性加权转化为一个单目标函数，转化时难以协调各目标函数值，加权系数的设定具有盲目性，且无法产生多个可行解，用户没有可选择余地；文献[9-10]将QoS全局最优动态服务选择问题转换为多目标优化问题，但前者采用较复杂的遗传算法，收敛速度较慢；后者利用粒子群算法求解，但对非支配解集的多样性考虑不足，优化解的质量有待提高。

针对多目标粒子群算法存在非支配解集多样性差、易陷入局部最优等缺陷，本文改进传统多目标粒子群优化(Multi-objective Particle Swarm Optimization, MOPSO)算法，提出一种基于混沌多目标粒子群优化算法(Chaotic MOPSO,CMOPSO)的动态服务选择实现方法。将云计算环境下的服务动态选择问题转化为带QoS约束的多目标服务组合优化问题，通过同时优化组合服务的多个QoS参数，产生一组满足约束条件的非支配解。用户可以根据实时需求选择最满意的解，而未被选中的非支配解则作为备选方案，以供所选组合服务失效时启用，保证用户获得满足要求的高质量云服务。

2 服务组合优化问题描述

在云计算环境下的服务选择问题中，服务组合流程是由一组服务节点按照一定的逻辑关系组成的，服务节点并不是具体的服务实例，而是一组具有相同功能描述和接口信息的候选服务实例的抽象，各候选服务拥有不同的QoS。假设一服务组合流程模型包含个服务节点，每个节点S有n个候选服务，服务组合流程模型如图1所示。

图1 服务组合流程模型

表1 基本结构的QoS计算公式

QoS全局最优的服务动态选择就是在组合流程模型执行过程中，从各个服务节点对应的候选服务集中选择具体的服务实例组成一个可执行的组合服务，使组合服务在满足特定的QoS约束情况下，多个目标(QoS参数)达到最优。为阐述方便，本文将执行时间，执行费用作为2个目标准则，希望得到最小的执行时间和最少的执行费用。将服务可靠性、服务信誉作为2个约束条件，表明该组合服务的所要求的最低可靠性和信誉度。一个带约束的多目标服务组合优化模型可描述为：

在多数情况下，由于服务QoS属性之间具有不可公度性和矛盾性等特点，造成服务组合优化各目标函数之间相互冲突，无法同时使多个目标均达到最优。因此多目标组合优化问题的结果不是单一解，而是满足约束条件下的一组非支配解。以下介绍多目标优化中常用的3个基本定义[11]：

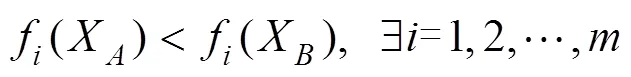
定义3(非支配解集) 非支配解集是指所有非支配解的集合，也称Pareto最优解集，定义如下：

3 混沌多目标粒子群优化算法

MOPSO在求解多目标优化问题时取得很好效果，但是仍存在以下问题：优化问题的非支配解分布不均匀，难以保持解集的多样性；容易陷入局部最优，出现早熟收敛情况。因此，本文利用混沌序列初始化粒子群，采用基于信息熵的多样性保持策略，确保非支配解分布均匀；在算法执行后期，当种群多样性丢失时，引入混沌扰动机制，增强种群多样性，提高算法全局寻优能力，避免陷入局部最优。

3.1 粒子群初始化

粒子群的初始化需要使粒子均匀分布在解空间里，扩展可行解的搜索范围，有助于提高算法求解效率和解的质量。混沌是自然界广泛存在的一种非线性现象，具有随机性和遍历性等特性，已被广泛应用随机优化[12]。因此本文利用混沌序列初始化粒子群，提高种群的多样性和搜索的遍历性，这里采用简单的一维Logistic混沌映射模型进行粒子群的初始化，其定义如下：

3.2 粒子速度和位置的更新

3.3 非支配解集的更新与维护

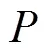
(2)根据粒子的信息熵计算2个粒子之间的相似程度：

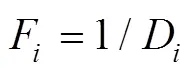
通过基于信息熵的适应度计算可知，非支配解集中相似个体越多则个体适应度越小，因此将非支配解集内的粒子按适应度降序排列，当解集中的粒子数目超过预定的阈值，则删除排在后端的适应度小的粒子，使非支配解集中的粒子能够均匀分布，保证了解集的多样性。

3.4 局部最优位置和全局最优位置的选择

3.5 混沌扰动操作

非支配解集中粒子适应度越小相似个体越多，粒子越密集。当多样性较差时，种群容易陷入局部最优，种群中的粒子速度会趋于0，并向解集中适应度小的密集粒子聚集，导致种群出现停滞现象，从而失去寻优能力。因此，为了提高种群多样性，避免种群陷入局部最优，将混沌的思想引入粒子群算法中。

当种群的多样性低于预先设定的阈值时，选择解集中排在前端/2个适应度大的稀疏粒子，对每个粒子进行多次混沌扰动，产生该粒子的多个邻域点，并根据支配关系选出这些邻域点中的非支配粒子，若存在多个非支配粒子，则随机选取其中一个作为新的粒子。经过混沌扰动操作可得到/2个新粒子，随机替代种群中的/2个粒子，且保持这些粒子当前的搜索速度和局部最优位置不变。具体实现过程如下：

(1)监测种群多样性是否满足预定阈值，种群的多样性测量公式如下：

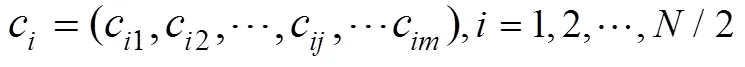
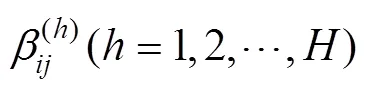
(3)求粒子每一维位置变量上产生的扰动偏差：

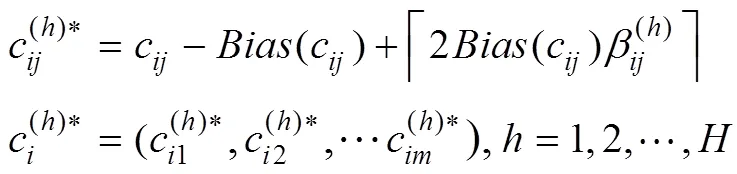
通过以上混沌扰动机制，在解集的稀疏粒子附近产生许多新的粒子，引导种群向解集的稀疏空间探索，增强了种群的多样性，避免种群陷入局部最优的束缚，使种群重新获得寻优能力，快速地向Pareto最优解集收敛，克服了算法易陷入局部最优的缺点。

3.6 算法流程

求解服务组合优化的CMOPSO算法流程如图2所示。

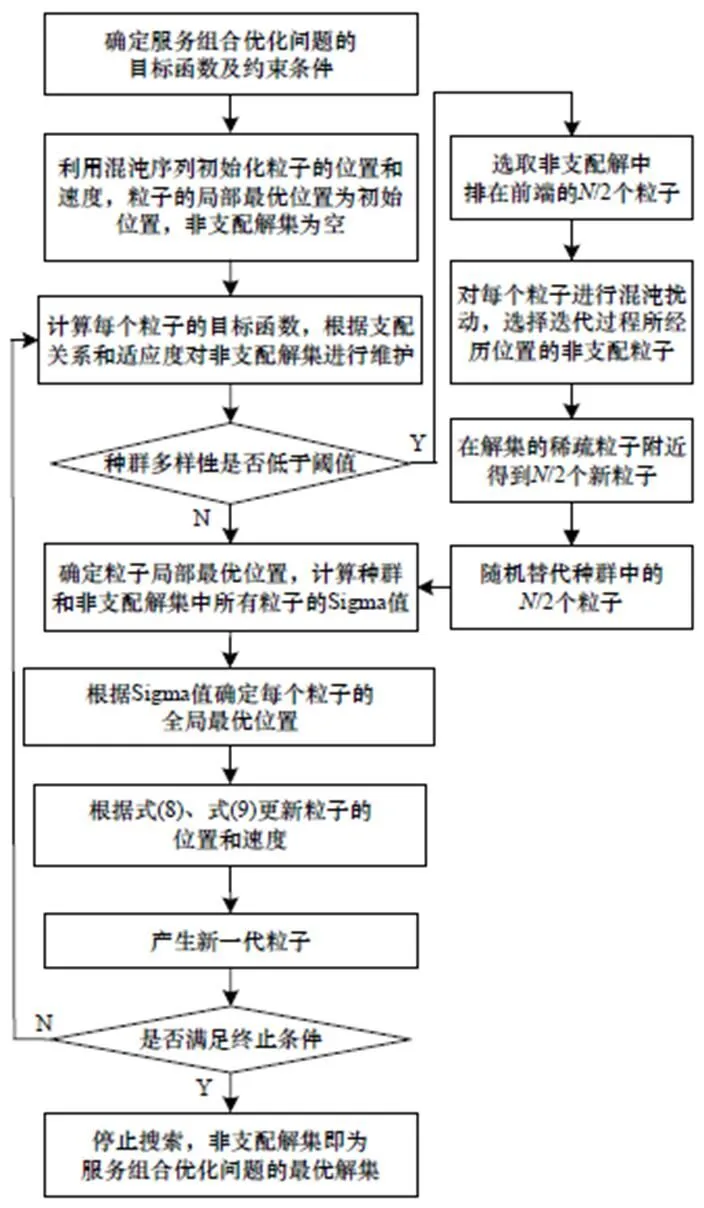
图2 CMOPSO算法流程

4 仿真实验与分析

本文从算法收敛性和优化解的质量2个方面对CMOPSO与MOPSO的求解结果进行对比分析。图3和图4分别显示了2种算法的迭代收敛过程和优化解的分布情况。

从算法迭代收敛过程来看，在迭代前期，CMOPSO和MOPSO收敛曲线基本一致，随着迭代过程的进行，CMOPSO搜索到的最优解数量明显多于MOPSO，CMOPSO在第35代收敛到非支配解规模上限，而MOPSO在第43代才完成算法收敛，因此，CMOPSO的收敛速度要优于MOPSO。

从优化解分布情况来看，MOPSO求的解分布比较集中，个体相似度比较高，部分可行解区域内不存在非支配解，相比之下，CMOPSO搜索到的非支配解分布比较均匀，保持了较好的多样性，优化结果更接近理想Pareto最优解集，求得组合优化解的质量好，能更好地满足用户的多样性需求。

通过以上实验分析可知，本文算法在求解服务选择问题时有较好的优化性能，有效避免算法早熟收敛现象，具有良好的全局寻优能力，能够快速地向理想的非支配解集收敛，并且保持优化解的多样性和分布的均匀性，最终得到一组满足约束条件的非支配解，用户可以根据不同偏好或实际情况，灵活地从非支配解集中选择合适的优化解。

图3 迭代收敛性比较

图4 非支配解分布情况比较

5 结束语

本文将云计算环境下的服务动态选择问题转化为带QoS约束的多目标服务组合优化问题，设计基于CMOPSO算法的动态服务选择求解方法，采用信息熵的理论保持了解集的多样性。在算法执行后期，当种群多样性丢失时，引入混沌扰动机制在解集的稀疏粒子附近产生许多新的粒子，提高种群的多样性和全局寻优能力，避免陷入局部最优，快速地向理想的非支配解集收敛。实验结果表明，相比传统MOPSO算法，CMOPSO算法的收敛性和解集多样性更好，能更有效地解决云计算环境下的服务动态选择问题。

[1] 罗军舟, 金嘉晖, 宋爱波, 等. 云计算: 体系架构与关键技术[J]. 通信学报, 2011, 32(7): 3-21.

[2] Majithia S, Walker D W, Gray W A. A Framework for Automated Service Composition in Service-oriented Archi- tectures[C]//Proc. of ESWS’04. Berlin, Germany: Springer- Verlag, 2004: 269-283.

[3] Zeng Liangzhao, Benatallah B, Dumas M. Quality Driven Web Service Composition[C]//Proc. of the 12th International Conference on World Wide Web. Budapest, Hungary: ACM Press, 2003: 411-421.

[4] Yu Tao, Lin K J. Service Selection Algorithms for Composing Complex Services with Multiple QoS Constraints[C]//Proc. of the 3rd International Conference on Service Oriented Computing. Amsterdam, Holland: Springer-Verlag, 2005: 130- 143.

[5] Ran Shuping. A Model for Web Services Discovery with QoS[J]. ACM SIGecom Exchanges, 2003, 4(1): 1-10.

[6] Liu Yutu, Ngu A H, Zeng Liangzhao. QoS Computation and Policing in Dynamic Web Service Selection[C]//Proc. of the 13th International Conference on World Wide Web. New York, USA: ACM Press, 2004: 66-73.

[7] 古凌岚, 孙素云. 基于遗传算法的组合服务选择方法[J]. 计算机工程与设计, 2011, 32(11): 3877-3880.

[8] 董元元, 倪 宏, 邓浩江, 等. QoS全局最优化的服务选择策略[J]. 小型微型计算机系统, 2011, 32(3): 455-459.

[9] 刘书雷, 刘云翔, 张 帆. 一种服务聚合中QoS全局最优服务动态选择算法[J]. 软件学报, 2007, 18(3): 646-656.

[10] 孙黎阳, 林剑柠, 毛少杰. 基于改进粒子群优化算法的网络化仿真任务共同体服务选择[J]. 兵工学报, 2012, 33(11): 1393-1403.

[11] 郑金华. 多目标进化算法及其应用[M]. 北京: 科学出版社, 2007.

[12] 张春慨, 徐立云, 邵惠鹤. 改进混沌优化及其在非线性约束优化问题中的应用[J]. 上海交通大学学报, 2000, 34(5): 593-595.

[13] 崔逊学, 林 闯. 基于多目标遗传算法的多播服务质量路由优化[J]. 计算机研究与发展, 2004, 41(7): 1144-1150.

[14] Mostaghim S, Teich J. Strategies for Finding Good Local Guides in Multi-objective Particle Swarm Optimization[C]// Proc. of 2003 IEEE Swarm Intelligence Symposium. Indianapolis, USA: IEEE Press, 2003: 26-33.

编辑 金胡考

Cloud Service Selection Based on Chaotic Multi-objective Particle Swarm Optimization Algorithm

WANG Na, WEI Bo, WANG Jin-dong, ZHANG Heng-wei

(Institute of Cipher Engineering, PLA Information Engineering University, Zhengzhou 450001, China)

With the explosive number growth of services in cloud computing environment, how to select the services that can meet user’s requirement from the services which have same or similar function becomes the key problem to be resolved in cloud computing. So a multi-objective service composition optimization model with Quality of Service(QoS) restriction is built, and since some disadvantages of the traditional Multi-objective Particle Swarm Optimization(MOPSO) algorithm, such as less diversity of solutions and falling into local extremum easily, a method of Chaotic MOPSO(CMOPSO) algorithm is proposed. This algorithm uses the information entropy theory to maintain non-dominated solution set so as to retain the diversity of solution and the uniformity of distribution. When the diversity of population disappears, it introduces chaotic disturbance mechanism to improve the diversity of population and the ability of global optimization algorithm to avoid falling into local extremum. Experimental result shows that the astringency and the diversity of solution set of CMOPSO algorithm are better than traditional MOPSO algorithm, and it can solve the problem of service dynamic selection under cloud computing environment more efficiently.

cloud computing; service selection; Quality of Service(QoS); Multi-objective Particle Swarm Optimization(MOPSO) algorithm; information entropy; chaotic

1000-3428(2014)03-0023-05

A

TP391.9

河南省科技攻关计划基金资助项目(122102310003)。

王 娜(1970－)，女，副教授、硕士，主研方向：服务计算，信息安全；卫 波，硕士研究生；王晋东，教授；张恒巍，讲师、博士。

2013-09-25

2013-10-30 E-mail：weibo7516@sina.com

10.3969/j.issn.1000-3428.2014.03.005