井下套管围压及第四等效应力分析
王小增,屈 展,窦益华
(1.西北工业大学,西安710072;2.西安石油大学,西安710065)
专题研究
井下套管围压及第四等效应力分析
王小增1,屈 展2,窦益华2
(1.西北工业大学,西安710072;2.西安石油大学,西安710065)
随着油田开采期限的延长和增产措施的应用,地应力产生粘弹性围岩蠕变造成套管围压的增加是套管损坏的主要原因之一。建立了固井段套管、水泥环和围岩的地质力学模型,得出了套管第四等效应力和围压的解析解;建立了套管、水泥环和围岩的有限元分析模型,得出了套管围压与第四等效应力的数值解。给定工况,远地应力作用下套管等效应力解析解比数值解大3.0%;套管围压解析解和数值解差别小于0.3%。建立的有限元模型和推导的计算公式可以分析地应力作用下套管的围压及第四等效应力。
套管;水泥环;围岩;围压;第四等效应力
国内外油气田开发过程中普遍存在套管损坏问题,例如挤扁,缩颈和错断等。套管损坏原因复杂[1-3],其中地应力作用下套管所受的围压超过其承载能力是套管损坏的主要原因。现场研究表明,由于地应力作用下固井段套管周围岩石的蠕变,油气井投产后套管的外载荷比刚完井时大[4-7]。为确保固井段套管不被损坏,保证油气井安全生产,分析远地应力作用下套管的围压及第四等效应力分布是十分必要的[8-9]。
建立了弹性围岩中固井段套管、水泥环和围岩的地质力学模型。通过对模型的基本假设,以弹性理论为基础,应用位移和径向应力连续条件,得出了套管围压和第四等效应力分布的解析解。建立了套管、水泥环和围岩的有限元分析模型,确定了套管围压和第四等效应力的数值解,并和解析解进行了对比分析。
1 套管和水泥环及围岩弹性状态分析
1.1 远地应力作用下套管力学分析模型
固井后,套管通过水泥环与地层紧密结合在一起。图1为远地应力作用下套管、水泥环和围岩的力学分析模型。其中:a为套管内半径,mm;b为套管外半径,mm;c为水泥环外半径,mm;po为远地应力,MPa;pi为套管内压,MPa。为能够得到套管围压和第四等效应力的解析解,结合井下实际情况做4个基本假设:
1) 套管、水泥环和地层为连续、均匀、各向同性的弹性体。
2) 套管和水泥环、水泥环和井壁之间完全接触,在结合处位移和径向应力连续。
3) 固井状态下,套管内表面为自由表面,套管体力不计。
4) 距离套管中心无穷远处为远地应力。
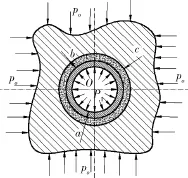
图1 远地应力作用下套管地质力学模型
1.2 套管弹性状态解答
套管内部受到液柱压力pi的作用,外壁受到远地应力产生的围压po的作用。基于前面基本假设,固井后的套管处于平面应变状态。在极坐标(r,φ)下,套管的弹性状态张量表示为:
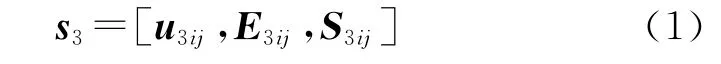
式中:E3ij为套管应变张量;u3ij套管的位移张量;S3ij为套管的应力张量。

由弹性力学理论可得,套管径向应力S3rr,环向应力S3φφ和轴向应力S3zz分量分别为:

套管的径向位移分量u3r为:
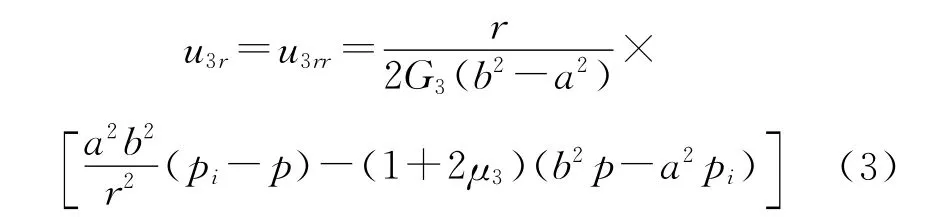
式中:E3为套管弹性模量,MPa;μ3为套管泊松比;G3为套管剪切弹性模量,MPa,G3=E3/(2(1+μ3))。
1.3 围岩弹性状态解答
围岩内壁为远地应力作用于水泥环的围压p2,外表面受到地层远地应力po的作用。基于前面基本假设,固井后的地层处于平面应变状态。围岩在极坐标(r,φ)下的弹性状态张量表示为:

式中:E1ij为围岩应变张量;u1ij为围岩位移张量;S1ij为围岩应力张量。
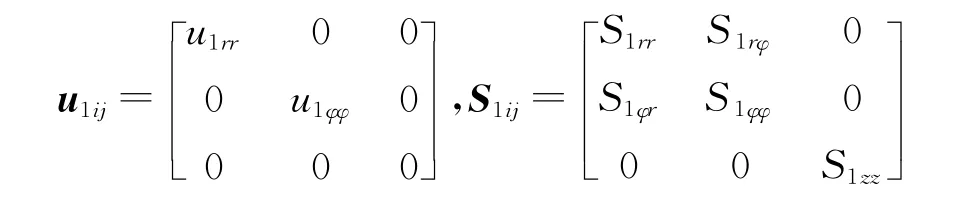
以井筒中心点O为圆心,假设存在半径趋于无穷大的圆。因地应力均匀作用于水泥环,则围岩相当于内壁半径为b,外壁半径为无穷大,受内压p2和外压po作用的圆筒。由弹性力学理论可得,围岩径向应力S1rr,环向应力S1φφ和轴向应力S1zz分别为:

围岩径向位移分量u1r为:
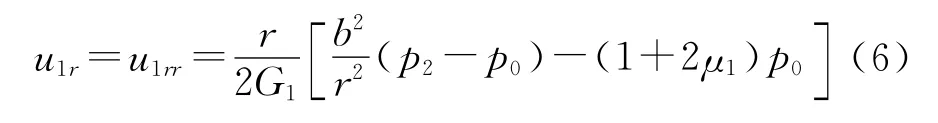
式中:E1为围岩弹性模量,MPa;μ1为围岩泊松比;G1为围岩剪切弹性模量,G1=E1/(2(1+μ1)),MPa。
1.4 水泥环弹性状态解答
水泥环内表面受与套管外部接触压力p的作用,外表面受围压p2的作用。基于前面基本假设,固井后的水泥环处于平面应变状态。水泥环在极坐标(r,φ)下的弹性状态张量表示为:
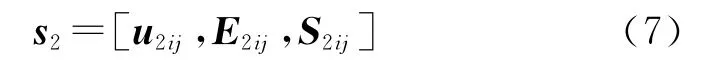
式中:E2ij为水泥环应变张量;u2ij水泥环位移;S2ij为水泥环应力张量。
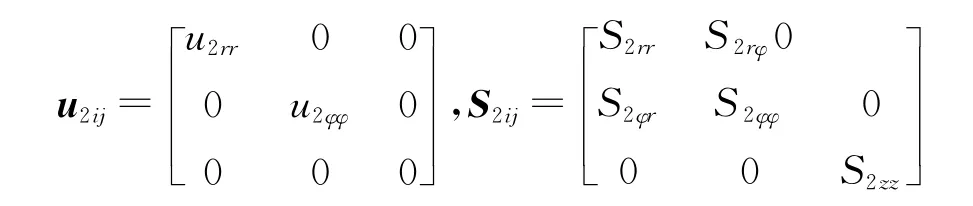
由弹性力学理论可得,水泥环径向应力S2rr,环向应力Sφφ和轴向应力S2zz分量分别为:

水泥环径向位移分量u2r为:

式中:E2为水泥环弹性模量,MPa;μ2为水泥环泊松比,G2为水泥环剪切弹性模量,MPa,G2=E2/(2(1+μ2))。
2 套管和水泥环围压分析
固井后,水泥环将套管与地层紧密结合在一起,在套管和水泥环、水泥环和围岩的2个交界面处完全接触,其径向位移连续,即有:
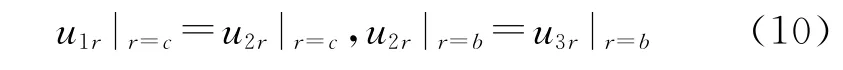
将式(3)、(6)、(9)带入径向位移连续条件式(10),可以求出弹性围岩作用下,套管所受的围压p和水泥环所受的围压p2:

式中:


3 套管第四等效应力的数值解
套管、水泥环和地层的有限元模型如图2所示。套管、水泥环和地层采用了Plane42单元类型,划分为映射网格。因为系统的对称性质,取套管、水泥环和地层力学分析模型的四分之一进行有限元分析。套管和水泥环、水泥环和地层之间为完全接触,不会发生相对滑动。分析中用到的套管、水泥环和地层的物理和几何参数如表1所示。
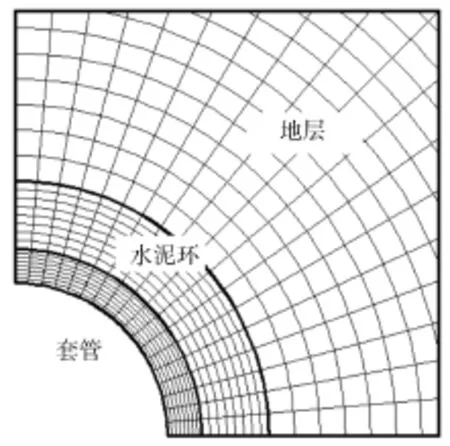
图2 套管和水泥环及地层的有限元模型
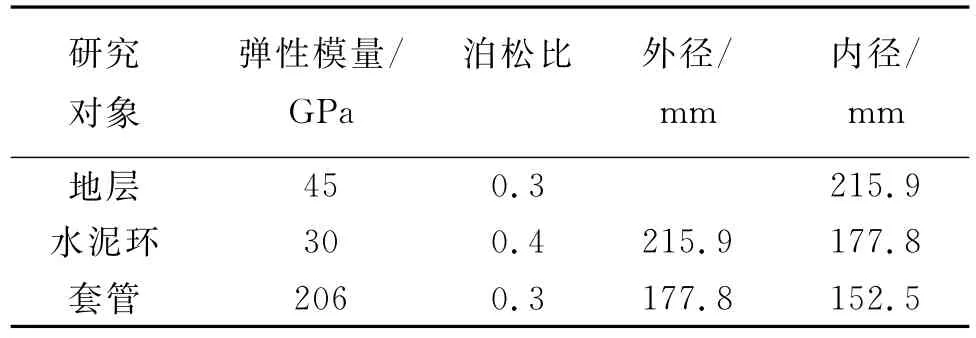
表1 套管和水泥环及地层物理和几何参数
某井试油工况下,地层压力为110 MPa(5 000 m井深,压力梯度取22 MPa/km),井底套管内压力为30~50 MPa。5 000 m井深,放喷求产时天然气压力梯度为3 MPa/km,井口压力为15 MPa,则井底套管内压力为30 MPa。井口压力增加到35 MPa,井底套管内压力为50 MPa。套管规格为177.8 mm×12.65 mm,钢级P110,下入约5 000 m深井中。钻头直径为215.9 mm(8⅟²英寸),井眼扩大系数取1.1、1.2、1.3、1.4、1.5,确定水泥环的厚度。试压值取套管抗内压强度的80%,套管内最多替成清水。若为低产气,井口压力低至15 MPa,井底压力低至30 MPa。在此工况下分析套管围压与应力、水泥环围压与第四等效应力。图3为套管等效应力分析云图,套管内表面第四等效应力518 MPa,套管外表面第四等效应力426 MPa。水泥环内表面第四等效应力99.6 MPa,水泥环外表面第四等效应力为99.4 MPa。套管和水泥环内部径向应力为压应力,从内到外逐渐增加。

图3 套管第四等效应力云图
4 井中套管模型的解析解和数值解对比
根据式(1)~(12)计算远地应力作用下套管和水泥环围压和第四等效应力的解析解,根据建立的套管、水泥环和围岩有限元模型,得到围压和第四等效应力的数值解,进行有限元数值解和解析解的对比分析。图4为套管第四等效应力理论与数值解对比,远地应力作用下套管第四等效应力解析解略大于其数值解值,相差小于3%。图5为套管围压解析解与数值解对比,远地应力作用下,内压小于40 MPa套管围压数值解略小于其解析解,套管内压大于40 MPa时,反之。套管围压数值解和解析解值相差不超过0.3%。

图4 套管第四等效应力解析解与数值解
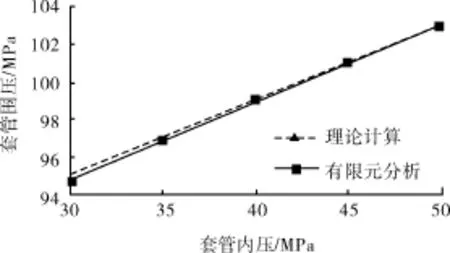
图5 套管围压解析解与数值解
5 结论
1) 根据建立的固井段套管、水泥环和围岩的力学模型得出了套管、围岩和地层围压和第四等效应力分布的解析解;根据套管,水泥环和地层的有限元模型得出了套管围压和第四等效应力的数值解。
2) 远地应力和内压共同作用下,套管第四等效应力解析解比其数值解大3.0%;
3) 远地应力和内压共同作用下,当套管内压小于40 MPa时套管围压解析解略大于其数值解;套管内压大于40 MPa,反之;套管围压理论和数值解之差小于0.3%。
4) 套管和水泥环围压和第四等效应力的解析解和数值解差别较小,建立的有限元模型和得到的计算公式可以分析地应力作用下套管的围压及第四等效应力分布。
[1] Xinpu Shen.Numerical analysis of casing failure under nonuniform loading in subsalt wells paradox basin[C].ARMA 11-176,2011.
[2] Mackay,F.,Inoue,N.Geomechanical effects of 3D vertical salt well drilling by FEA[C].ARMA 08-041,2008.
[3] Yong Li,Shouqiong Liu,Zhaohui Wang.Analysis of cement sheath coupling effects of temperature and pressure in non-uniform insitu stress field[C].SPE 131878,2010.
[4] 窦益华,樊正祥,邓跃辉,等.用遗传积分法计算蠕变地层中套管的围压[J].石油钻采工艺,1996,18(4):5-14.
[5] Willson S M,Fossum A F,Fredrich J T.Assessment of salt loading on well casings[J].Society of Petroleum Engineers,2003(3):13-21.
[6] 殷有泉,李志明,张广清,等.蠕变地层套管载荷分析研究[J].岩石力学与工程学报,2004,23(14):2381-2384.
[7] 刘合,王秀喜.大庆油田泥岩粘弹性本构方程及套管受力计算[J].中国科学技术大学学报,2005,35(1):118-123.
[8] 于桂杰,王瑞和.基于长效地应力机制下套管围压的分析计算方法[J].石油矿场机械,2010,39(5):1-6.
[9] 李平恩,殷有泉,苏先.流变地层地应力场中套管载荷的解析解[J].北京大学学报,2007,43(1):11-16.
[10] Feng Qian,Deli Gao.A mechanical model for predicting casing creep load in high temperature wells[J].Journal of Natural Gas Science and Engineering,2011(3)530-535.
Confining Pressure and Von Mises Stress of Downhole Casing
WANG Xiao-zeng1,QU Zhan2,DOU Yi-hua2
(1.Northwestern Polytechnical University,Xi’an 710072,China;2.Xi’an Shiyou University,Xi’an 710065,China)
With the extension of production period and the application of well stimulation in oil field,the confining pressures which result from the in-situ stress often lead to the damage of casing.Considering casing,cement and rock in cemented sections,a geomechanical model is established,while analytical solutions of Von Mises stress and confining pressure are obtained.A finite element method is developed to obtain the numerical solutions.The result shows that analytical and numerical solutions are almost equal.Under the action of the in-situ stress,compared to the numerical solution,the analytic solution of von Mises stress of casing is slightly increased by 3%.The difference between the analytic and numerical solution is less than 0.3%.Developed the finite element model of casing,cement and formation and analytic formulas can be used to analyze the confining pressure and Von Mises stress of casing under the action of the in-situ stress.
casing;cement;formation;confining pressure;von mises stress
TE931.202
A
10.3969/j.issn.1001-3482.2014.12.001
1001-3482(2014)12-0001-04
2014-06-01
国家自然科学基金项目“力学化学耦合下泥页岩井壁蠕变损伤失稳研究”(51174162)
王小增(1973-),男,辽宁绥中人,副教授,硕士,博士研究生,2003年毕业于西安石油大学机械电子工程专业,主要从事井筒完整性评价方面的研究,E-mail:21772778@qq.com。

