动力钳开口齿轮组结构优化设计与模态分析

刘志刚

（江苏如石机械有限公司，江苏如东226406）

设计计算

动力钳开口齿轮组结构优化设计与模态分析

刘志刚

（江苏如石机械有限公司，江苏如东226406）

开口齿轮是钻杆动力钳钳头部分的重要传动部件。目前，开口齿轮组的结构设计方法单一，造成体积较大。针对开口齿轮组的结构与布局，通过选取合适的结构参数作为输入变量，依据齿轮啮合条件和接触、弯曲疲劳强度等构造约束条件，以总体尺寸为优化目标，采用改进的粒子群算法（PSO）对开口齿轮组进行结构优化设计。分别将优化前后结构建模并导入ANSYS Workbench，通过模态分析对优化结果进一步论证。结果表明：采用改进PSO方法优化后的模型体积更小，同时各阶固有频率得到提高，说明该方法能够有效指导钻杆动力钳的开口齿轮结构设计，具有良好的工程应用价值。

钻杆动力钳；开口齿轮；结构优化；模态分析

随着石油、天然气等矿物能源的开采量增加，深井、超深井逐渐增多，使得修井机械装备不断发展，其中钻杆动力钳得到广泛开发与应用。开口齿轮是开口式动力钳钳头部位的主要受力部件，作为动力传递与钳头咬紧机构，开口齿轮组的结构参数与布局对于动力钳的力学性能及外观尺寸等都有着重要影响［1］。开口齿轮传动系统设计主要包括齿轮参数设计和传动机构位置布局设计。传统的传动齿轮参数设计方法需要参照标准传动齿轮设计规范设计，并考虑材料强度与齿轮载荷加入相应的安全系数，最后进行校核［2］。另一方面对于开口齿轮传动机构的布局确定方法通常是在给定的安装条件下带入多组数据找出所有可能的布局参数，最后根据其他制约条件选择最优布局参数。由于以上设计过程很多参数依靠经验确定，没有明确优化目标，易造成钻杆动力钳钳头的传动机构体积过大，材料成本增加。因此需要以开口齿轮组构成的传动机构体积精简为目标，进行多参数的齿轮组结构优化设计。

结构优化设计目前已在工程应用领域广泛使用［3］，但在开口齿轮组的优化设计中存在一些问题：①依赖经验选取的参数较多，较难确定；②优化过程计算量大，效率较低；③容易陷入局部最优解。针对上述的组合优化问题，现代智能优化算法可以在约束条件内快速有效找出全局最优解，其中粒子群算法（PSO）是一种基于迭代的随机全局最优优化算法［4］，该算法通过粒子群在解空间追随最优粒子搜索最优解，相比于经典的遗传算法具有简单易行、精度高和收敛快等特点，适合应用于开口齿轮组结构的多参数优化设计。

1 基本设计参数

1.1 传动机构要求

由于开口齿轮组是4个直齿圆柱齿轮相互啮合，属于过约束齿轮机构，因此在设计开口齿轮组时要考虑正确的安装条件，否则会导致卡死、安装错位等现象，使齿轮组不能正常工作。开口齿轮的安装原理简图如图1所示，其中开口齿轮齿数Z3，开口宽度为b，两个对称分布的惰轮齿数Z2，小齿轮齿数Z1，O2O3与O1O3夹角为α，O1O2与O2O3夹角为β，O1O2与O1O3夹角为γ。

图1 开口齿轮组安装简图

根据文献［5］给出的4齿轮机构约束条件，结合图1进行分析可以得到开口齿轮组正确安装条件：

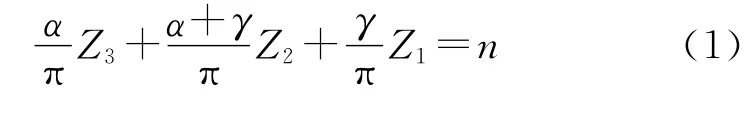
式中：da1，da2，da3分别为各齿轮齿顶圆直径。

在已知各齿轮模数和齿数时，要确定开口齿轮正确安装条件参数首先需要根据上述约束给出角度α的最大与最小值，并通过在该范围内对α多次试取值带入式（1）得到多组符合条件的n，最后根据其他制约条件选取α的最优值，并依此推导出其他参数，从而获得4齿轮开口齿轮组的正确安装条件。

除了安装条件，开口齿轮组各齿轮的模数、齿数以及齿宽等参数也会对最终总体机构体积和结构性能产生影响。所以设计开口齿轮传动机构需要综合考虑齿轮啮合原理和正确安装条件，并在此基础上进行优化。

1.2 原始设计参数

钻杆动力钳为开口式动力钳，最大适用管径216 mm。初始的开口齿轮组的基本参数包括：功率64 k W；输出转速4.2 r／min；传动比2.8；输出转矩135 k N·m。主要设计参数包括：开口宽度bk＝223.64 mm；啮合齿轮模数m＝12；开口齿轮齿数Z3＝67，齿宽b3＝100 mm；惰轮齿数Z2＝28，齿宽b2＝105 mm；小齿轮齿数Z1＝24，齿宽b1＝110 mm；夹角α＝31°。

式中：n为正整数，α、γ单位为rad。

2 结构优化条件

2.1 定义优化变量

通常情况下对于开口齿轮组的结构优化设计时需要考虑所有的相关参数，但同时也会增加计算和求解时的工作量与难度，所以只需要提取对优化目标影响较大的参数，精简优化问题的变量维数，便于问题求解并简化计算。这里对齿轮的压力角、齿顶高系数和顶隙系数均按标准直齿轮选取；开口齿轮的开口宽度是由最大管径决定的，因此该参数不做改变；一般啮合齿轮对中要求小齿轮宽度应比大齿轮宽5～10 mm，这里为了简化变量维数只设立开口齿轮Z3的齿宽系数φd为变量，而齿轮Z2和Z1齿宽的分别比齿轮Z3齿宽大5 mm和10 mm。因此开口齿轮的体积优化问题中关键变量参数最终可以确定为齿轮模数m，小齿轮齿数Z1，惰轮齿数Z2，开口齿轮齿数Z3，齿轮位置夹角α，开口齿轮齿宽系数φd。即：

2.2 约束条件确定

2.2.1 齿轮模数

由于传递大扭矩的开口齿轮模数不能过小，通过同类传动机构类比确定模数取值范围：

且x1取值按GB1357—1987标准圆柱齿轮模数选取。

2.2.2 齿数

各齿轮齿数都应取整数，同时应满足不产生根切，根据具体工况分析有：

并且允许传动比前后有0.05的误差：

2.2.3 齿宽

针对齿轮齿宽有：b＝φdd1。大齿轮齿宽系数φd选取范围0.2～2.4，d1为小齿轮分度圆直径，小齿比大齿宽5～10 mm，这里为简化程序取5 mm，所以只需对开口齿轮齿宽系数定义约束：

2.2.4 齿面接触疲劳强度

齿面接触疲劳强度校核公式为：

式中：ZE为弹性系数；ZH为区域系数；Zε为重合度系数；K为载荷系数；T1为小齿轮扭矩；μ为接触大齿轮齿数与小齿轮齿数之比。

开口齿轮组有2类啮合情况，分别带入优化变量参数简化有：

2.2.5 齿根弯曲疲劳强度

式中：YFa为齿形系数，Ysa为应力修正系数，Yε为重合度系数，σFP为许用弯曲应力。

分别带入齿轮的变量参数简化后有：

2.3 适应度函数确定

开口齿轮组以及动力钳钳头尺寸主要是由齿轮

齿根弯曲疲劳强度校核公式为：Z1和Z3中心距、Z2和Z4中心距和齿宽来确定，以此为依据，构造衡量开口齿轮组体积的适应度函数如下：

函数f（x）越小表明齿轮组总体积越小，以约束范围内全局最小值作为优化目标。

3 基于改进PSO的开口齿轮组结构优化设计

针对开口齿轮组结构的传统优化方法，一般通过经验多次试取或者对结构做近似分析，但传统优化方法往往不具备全局性，容易陷入局部最优解，而且随着设计变量增加和约束范围增大，优化分析的效率显著降低，优化结果也不理想。对于这类多条件约束的单目标优化问题，更适合智能优化算法解决。PSO算法是一种利用群体智能的随机优化算法，具有收敛快、易实现、全局搜索能力强等特点［6］。

3.1 PSO优化算法

PSO算法受鸟群觅食行为启发，将约束范围内的一个解称为粒子，而多个粒子构成的种群称为粒子群。假设xi＝（xi1，xi2，…，xin）为粒子i在解空间中的n维坐标，同时每个粒子都有决定其移动方向与距离的飞行速度向量Vi＝（Vi1，Vi2，……，Vin）；在第t次迭代过程中粒子i自身所找到的最优解的位置为Pi（t）＝（Pi1，Pi2，…，Pin），称为个体极值，函数P为适应度函数；整个粒子群搜索到的最优解位置Pg（t）＝（Pg1，Pg2，…，Pgn），称为全局极值。对于开口齿轮组结构体积最小的优化问题，目标函数值越小，对应的适应函数值越好。标准的粒子群算法粒子的速度与位置更新公式如下［7］：

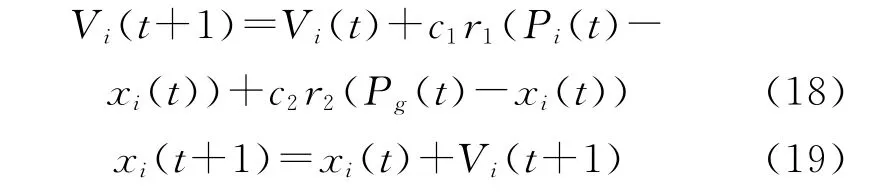
式中：c1、c2为加速常数，一般在0～2间取值；r1、r2为区间在（0，1）间的相互独立的随机函数。粒子速度Vi通常限定在［－Vmax，Vmax］。

3.2 改进的PSO优化算法

标准粒子群算法的求解主要研究所有粒子与种群中性能最优粒子的结构影响，但对于各粒子个体与领域粒子的关系及影响没有得到很好的体现。因此为了平衡算法的收敛速度和优化精度，对粒子速度更新引入惯性权重ω和周围极值的影响，粒子速度更新公式为：

式中：Pj（t）为当前粒子跟踪周围粒子的极值，c3为权重系数。

惯性权重ω较大可提高全局搜索能力，较小时可增强局部搜索能力。因此通过带入最大和最小权值ωmax、ωmin对ω作非线性调整：

式中：t为当前迭代数，Gen为总迭代数。此外根据文献［8］可知指数n取0.5时寻优能力最好。

3.3 算法流程

1） 根据开口齿轮组的优化变量X对粒子群初始的随机位置和速度进行初始化设定。

2） 依据式（17）计算各粒子的适应函数值。

3） 对每个粒子经历的位置适应值进行比较，将最优值作为当前粒子的局部最优解。

4） 对每个粒子将其当前的局部最优解与群体中的最优解比较，将最优解作为当前的全局最优解。

5） 根据式（20）、（21）对所有粒子位置和速度更新。

6） 若迭代次数未达到上限Gen则返回步骤2），否则结束。

4 优化结果分析

整个优化设计的硬件环境CPU为i5 2.5GHz内存4G的笔记本，软件平台为MATLAB7.0。PSO算法参数选取：学习因子c1＝c2＝1.4962，c3＝1.2，惯性权重ωmax＝0.729 8，ωmin＝0.316 2，种群数popsize＝50，最大迭代次数Gen＝100。算法全局最优值迭代曲线如图2。

图2 改进PSO算法迭代曲线

可以看出粒子群在第12次迭代时收敛到最优适应值。具体参数圆整后与原始参数对比如表1。

表1 优化前后参数对比

经过验证优化后参数符合设计要求，并且相比于原始设计参数体积更小，目标值相比于原始目标值减少了27.64%。

5 ANSYS Workbench开口齿轮组模态分析

通过在Pro／E环境下建立优化前后4齿轮的啮合模型，进一步导入ANSYS Workbench的静力学模态分析“Modal”模式中进行模态分析，对比优化前后结构性能。

1） 添加材料 开口齿轮组的齿轮材料均为42Cr Mo，弹性模量2.06×1011Pa，泊松比0.3，密度7 800 kg／m3。

2） 设定接触类型 齿轮传动为有摩擦接触类型，故定义为Frictional，摩擦因数0.06。

3） 网格划分 齿轮组的网格划分类型为自由划分，网格大小为3 mm。

4） 施加约束 对各个齿轮约束x，y，z方向平动自由度与x，y转动自由度，只保留轴向的z方向转动自由度。

5） 求解结果 一般对于齿轮的模态分析的阶数不需要太高，这里设定分析前5阶的模态。并在“solution”中选择“Insert｜Deformation｜Total”，添加1～5阶振动模态下的形变情况，并通过“solve”选项求解。得到优化前后各模态下形变云图，选取效果较为明显的的1、3、4阶模态下形变对比如图3所示。各阶固有频率与变形量均列在表2中。

图3 优化前后模态分析

从图3结果可以看出，无论优化前后各阶模态下最大形变位置都相差不多，形变主要集中在开口齿轮缺口附近齿上，其中1阶形变方向主要沿开口齿轮径向，而3和4阶形变方向沿开口齿轮轴向。在3阶和4阶的形变云图中可以看到各齿轮重要部位啮合处都在形变较小区域，而且优化后啮合处形变数值明显比优化前小。

表2 优化前后模态分析结果对比

从表2中的数据可以看出，优化后的开口齿轮组各阶的固有频率相比于原始参数下的齿轮组结构有提高，而3、4和5阶模态下的最大变形量也有所减少，充分说明优化后的开口齿轮组的结构性能及工作稳定性均有所提高。

6 结论

1） 针对钻杆动力钳开口齿轮组的设计参数与结构布局，创新提出动力钳开口齿轮结构优化设计方法。以体积最小为优化目标，采用基于惯性权重ω和周围极值的改进PSO算法求解结构优化问题，准确获取开口齿轮组体积最小时的结构与布局参数。

2） 采用ANSYS Workbench软件进行模态分析，验证了动力钳开口齿轮结构优化设计后能够减小体积，提高各阶模态下固有频率，同时高阶模态下最大变形量减少。

3） 通过本文的优化设计方法能够极大提高动力钳开口齿轮的设计效率，简化计算，减少试验成本，并且在保证设计结果安全可靠基础上精简体积，对于钻杆动力钳优化设计具有指导意义。

4） 当前的钻杆动力钳开口齿轮优化设计仅局限于齿轮组的尺寸与布局，而完整的开口齿轮组还需要包含转轴、上盖等部件，而整体部件的优化设计与分析更具有实际意义。因此，今后将研究开口齿轮组整体结构优化设计以及动力钳的整机模态分析。

［1］ 吴其尧.开口齿轮微变形的消除方法［J］.科技创新与应用，2012（32）：37-38.

［2］ 刘继权.钻杆动力钳性能分析与扭矩监控系统的研究［D］.阜新：辽宁工程技术大学，2007.

［3］ 胡桂川，刘敬花.基于CAE分析的机械结构优化设计［J］.机械设计与研究，2011，27（3）：73-76.

［4］ Yuguo Wu.A New Kind of Optimization Method for Gear Design［C］／／Digital Manufacturing＆amp；Automation III.2012：5-8.

［5］ 高翔，黄呜风，曹浪波，等.开口齿轮传动机构设计探讨［J］.石油矿场机械，2003，32（6）：37-39.

［6］ 郭广寒，王志刚.一种改进的粒子群算法［J］.哈尔滨理工大学学报，2010，15（2）：31-34.

［7］ KENNEDY J，EBERHART R C.Particle Swarm Optimization［C］／Proceedings of IEEE International Conference on Neural Networks，Piscataway，1995：1942-1948.

［8］ 张焱，高兴宝.一种改进的粒子群算法［J］.计算机工程与应用，2009，45（26）：58-59，93.

Structure Optimization Design and Modal Analysis of the Power Tong Notched Gears

LIU Zhi-gang
（Jiangsu Rushi Machinery Co.，Ltd.，Rudong 226406，China）

The notched gears are important transmission components of the drill pipe power tongs，but currently the methods for notched gear optimization are simple and there are no proper optimization methods.The improved PSO algorithm was used to optimize the design of the notched gear structure.The appropriate structure parameters were selected as input variables，and constraint conditions were built according to gear condition and bending fatigue strength etc.The optimization design was based on the overall size of the target.The models before and after optimization of notched gear were imported into ANSYS workbench for modal analysis，and the results illustrate that the optimized model is smaller and enhanced structurally，and the natural frequencies of the model is improved.The results can be concluded that the optimization method based on improved PSO can be considered as a valuable reference for the optimization design of notched gears and is with good engineering value.

drill pipe power tong；notched gear；structure optimization design；modal analysis

TE921.202

A

10.3969／j.issn.1001-3482.2014.12.007

1001-3482（2014）12-0026-05

2014-06-10

刘志刚（1966-），男，江苏如东人，高级工程师，现从事石油井口及工具的研制与管理工作。