哈林图Wiener指标的若干极值问题

刘顺琴

（福建师范大学闽南科技学院 福建泉州 362332）

哈林图Wiener指标的若干极值问题

刘顺琴

（福建师范大学闽南科技学院 福建泉州 362332）

一个连通图G的Wiener数(或Wiener指标)定义为G中所有(无序)顶点对的距离之和，给出了n阶哈林图中Wiener数的最小值和对应的极图；以及直径为3的树所对应的哈林图的Wiener数的最小值和最大值，并确定了相应的极图；最后，给出了哈林图Wiener数的一个不等式。

哈林图；Wiener指标；最大；最小

定义：哈林图是这样一类图，对于n(n≥4)阶的没有二度顶点的一棵树的平面嵌入，将其树叶按顺序连成一个圈，得到的平面图称为哈林图。

另外用 表示所有n阶哈林图的全体； 表示阶数为n(n≥6),直径为3的且在分支点的度数均大于等于3的树图所对应的哈林图的全体，如下图1所示(其中s+t=n-2,s≥t≥2)，并且定义如下的哈林图-n阶轮图L(n):

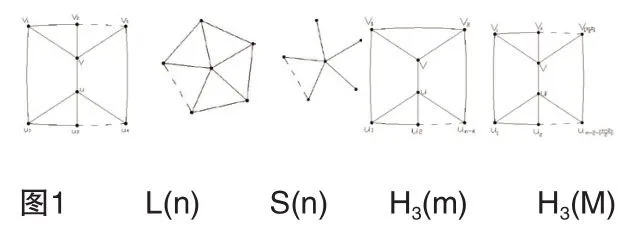
显然，L(n)是星形图S(n)(树)对应的哈林图，以上两个是n阶的直径为3的树对应的两个哈林图(H3(m)、H3(M))。

一、Wiener数最小的哈林图

证明：作为n(n≥4)阶树图，星图S(n)的叶子的个数为(n-1)．除星图之外，其它n阶树图的叶子数均小于n-1．因此，星图S(n)所对应的哈林图，即n阶轮图L(n)的总边数为2(n-1)，其它树图所对应的哈林图的边数均小于2(n-1).另一方面，在任何一个连通图G中，除了每条边所连接的两个顶点之间的距离为1之外，其余的顶点对之间的距离均不小于2，因此

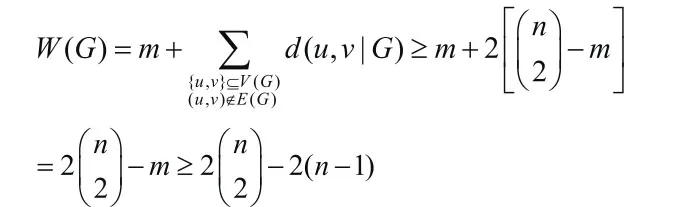
进一步地，当H是一个哈林图时，不难看出上述等号成立当且仅当H是轮图L(n)．定理证毕．

推论：n阶哈林图H有，W(H)≥(n-1)(n-2).

证明：n阶轮图L(n)中有2(n-1)个顶点对之间有边连接，剩

再由上面的定理1，推论自然成立.

二、直径为3的树对应的哈林极图

{u},{v},{u1,u2,……us},{v1,v2,……vt}, 对于H, 其直径小于等于3，故点与点之间的距离只有三种情况：距离为1，为2，为3。分别考虑这三种情况：

显然距离为1的点对的数目nd1即该图的边数m，所以

nd1=m=n-1+(n-2)=2n-3

距离为2的点对的数目由以下5个部分组成：

1.{u}和{v1,v2,……vt}, 其中u和{v1,v2,……vt}中的任何顶点距离均为2, 点对的数目为t；

2.{v}和{u1,u2,……us}，其中v和{u1,u2,……us}中的任何顶点的距离均为2, 点对的数目为s；

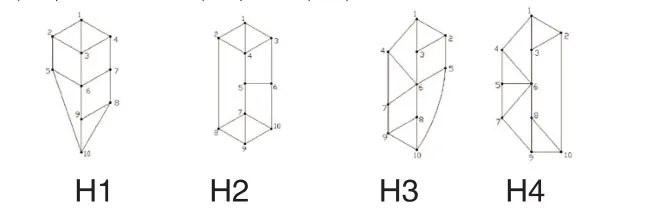
当树图的直径大于等于4时，在其对应的哈林图中，我们认为Wiener数最大和最小的哈林图并不唯一，下面我们分别给出了顶点数为10，直径为4的树图对应的哈林图，Wiener数最大两个图 和 ，Wiener数最小的两个图 和 :

W( H1)=W(H2)=85, W(H3)=W(H4)=83

三、不等式设T是满足分支点度数大于等于3的树，T有t片树叶，H是T对应的哈林图，则T和H的Wiener数之间存在着如下关系。

定理3: 设T是满足分支点度数大于等于3的树，T有t片树叶，H是T对应的哈林图，则W(H)≤W(T)-t.其中W(H)=W(T)-t当且仅当T是星图，而自然H是轮图。

证明：由于T有t片树叶，故不管这t片树叶按哪种顺序连接成一个圈使得T变成H时，总是加了t条边. 当两个树叶之间加一条边时，原本距离≥2的两个树叶的距离变成了1，故而每加一条边，距离至少少于1，加t条边，所以W(H)≤W(T)-t. 要使得等式成立，则要保证每加一条边时Wiener数刚好少1，则要求相邻的两个树叶之间的距离必须刚好为2，这就说明了相邻的两个树叶必须连接在同一个分支点上，也就是说所有的树叶必须连接在同一个分支点上，这样的树图就是星图，对应的哈林图当然是轮图. 证明完毕.

[1] L. B. Kier, L. H. Hall, The nature of structure-activity relationships and their relation to molecular connectivity, Europ. J. Med. Chem. 12 (1977) 307-312.

[2] X. Li, J. Zheng, A unified approach to the extremal trees for different indices, MATCH Commun. Math. Comput. Chem. 54 (2005) 195-208.

Some extremal problems of Halin graphs of Wiener index

Liu Shun-qin

(Minnan Science and Technology Institute of Fujian Normal University, Quanzhou Fujian,362332, China)

A connected graph G Wiener number (or Wiener) is defined as the G in all (disorder) vertex and distance. The pole figure of minimum values and the corresponding gives Wiener n order Halin graphs number; number and diameter of 3 Wiener corresponding to the tree Halin graphs of minimum and the maximum value, and determine the corresponding extreme graphs; finally, gives an inequality of Halin graphs of Wiener numbers

Harinto; Wiener index; maximum; minimum

O157.5

A

1000-9795（2014）05-0151-01

［责任编辑：刘丽杰］

2014-03-12

刘顺琴（1981-），女，福建人，讲师，从事图论方向的研究。