用特征多项式系数计算矩阵方幂的迹

张 卓

（西南大学数学与统计学院，重庆 400715）

用特征多项式系数计算矩阵方幂的迹

张 卓

（西南大学数学与统计学院，重庆 400715）

在矩阵特征多项式Lwverrier方法的基础上，利用特征多项式的系数计算矩阵方幂的迹，使得当矩阵未知或者阶数较大时计算的复杂度有所降低，并通过例子加以验证.

特征多项式；系数；矩阵；方幂；迹

迹作为矩阵的一个重要数字特征，在计算数学、逼近论以及估计等方面有着非常广泛的应用.求矩阵方幂的迹，可以按照矩阵乘法先求出矩阵的方幂，再求其主对角线元素之和.但是当阶数较大或者矩阵未知（仅已知特征多项式）时，要求得矩阵方幂的迹是相当复杂的.于是，此处就在特征多项式Lwverrier方法的基础上，利用特征多项式的系数直接计算矩阵方幂的迹.这样以来，问题就变得简单多了.

1 预备知识

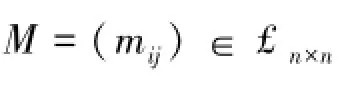
根据矩阵迹的定义，容易验证迹有如下性质［2］：（1）tr（M+N）=tr（M）+tr（N）；（2）tr（kM）=k tr（M）；（3）tr（M）=矩阵主对角线元素之和=所有特征值的和.

引理1［3］设n阶矩阵M的特征多项式

定义下列矩阵

引理1是用递推的方法证明特征多项式系数与矩阵乘积的迹之间的一些联系.文献［4］也是在此引理的基础上用矩阵方幂的迹给出了特征多项式系数的矩阵表示.由于在很多情况下直接求矩阵方幂的迹是相当复杂的，而特征多项式（系数）却可以用求伴随矩阵的方法很容易地计算出来.因此，可以利用特征多项式的系数反过来直接求矩阵方幂的迹.

2 用特征多项式的系数表示矩阵方幂的迹

定理1设n阶矩阵M的特征多项式

则

证明因为n阶矩阵M的特征多项式为

所以可以根据引理1定义一系列矩阵如式（1），并变形

因此

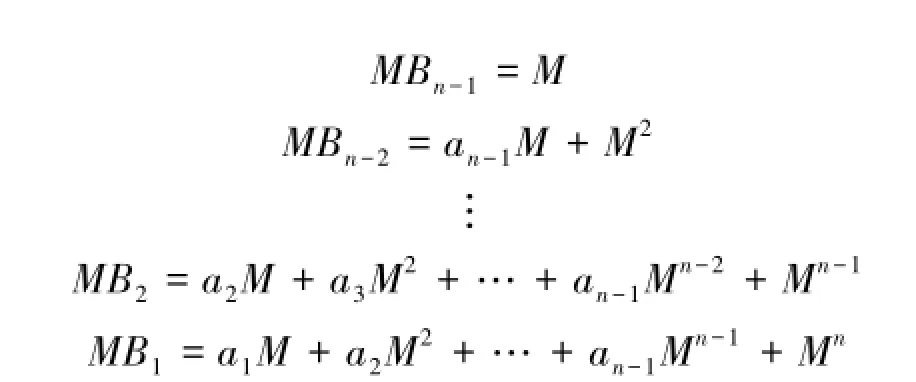
再由引理1中式（2）以及性质（1）（2）可得

依次把tr（M），tr（M2），…，tr（Mi-1）带入第i个方程，可得

例1已知3阶矩阵M的特征多项式p（λ）=λ3-10λ-9，求M，M2，M3的迹.

解设ai是p（λ）=λ3-10λ-9的i次项系数，则a3=1，a2=0，a1=-10，a0=-9，直接根据定理1可求得M方幂的迹为

解由于题目仅已知了矩阵而特征多项式未知，所以可以先用求伴随矩阵的方法算出M的特征多项式p（λ）=λ4-6λ3-4λ2，仍设ai为特征多项式p（λ）的i次项系数，于是a4=1，a3=-6，a2=-4，a1=0，a0=0.然后利用定理1求得M方幂的迹为tr（M）=6，tr（M2）=44，tr（M3）=288，tr（M4）=1 904.

3 小 结

求矩阵方幂的迹，既可以按照矩阵乘法先求出矩阵的方幂，再求其方幂的迹（主对角线元素之和），也可以先求出其特征多项式，再利用定理1的结论直接求其方幂的迹.前者仅适用于矩阵已知的情形，而当矩阵的阶数较大或者矩阵未知（仅已知特征多项式）时，后者的优势就显现出来了.当然，也可以通过编程使其变得更加简单明了.

［1］王萼芳，石生明.高等代数［M］.3版.北京：高等教育出版社，2003

［2］牛华伟，张厚超.关于矩阵迹的性质与应用［J］.宁波职业技术学院学报，2009（2）：41-43

［3］王卿文，杨家骐.“矩阵特征多项式的一种求法”的一个注记［J］.数学通报，1992（6）：35-36

［4］孙志和，窦在祥.特征多项式系数的矩阵表示［J］.青岛理工大学学报，2006，27（3）：112-115

On Computing the Trace of Matrix Power by Using Characteristic Polynomial Coefficient

ZHANG Zhuo
（School of Mathematics and Statistics，Southwest University，Chongqing 400715，China）

Based on characteristic polynomial Lwverrier method of a matrix，the trace of matrix power is computed by using characteristic polynomial coefficient so as to reduce computation complexity when a matrix is unknown or the order is larger，which is tested by examples.

characteristic polynomial；coefficient；matrix；power；trace

O151.21

A

1672-058X（2014）03-0027-03

责任编辑：李翠薇

2013-09-04；

2013-09-28.

张卓（1989-），女，河南邓州人，硕士研究生，从事计算数论研究.