Smith-RBF-PID控制算法在工业平缝机脚踏板调速模块中的应用
邓先智
(绵阳职业技术学院机电工程系 四川绵阳 621000)
在工业平缝机发展中,缝制效率是一个重要的课题。而缝制效率主要是由缝纫机的缝纫速度所决定。在缝制过程中,通过人工踩踏脚踏板控制缝纫机的启动、调速和结束缝制。高速工业平缝机控制系统对缝纫机的启动、停止和缝纫速度的技术要求非常严格。要求起动轻柔、迅速,升速从0 rpm到4 500 rpm的时间要小于100 ms;停针要迅速准确,速度从4 500 rpm减到0 rpm的时间小于120 ms。同时在调速过程中要求无级调速,速度变化要平稳。一般的系统在调速模块中采用的是PI[1]或改进的PID控制算法[2],此类算法虽然采取了高速和低速分段控制方法,但是当PID参数整定后,在这之间的控制过程都是固定不变的。而平缝机调速模块的伺服系统是一个多变量、非线性、强藕合、大滞后系统。在负载变化或者出现扰动时的滞后时间范围内,被控的参数是无法进行调整的,使得系统不能及时反应,立即补偿。致使产生较明显的超调量和需要较长的调节时间,无法满足系统要求。
Smith预估补偿控制是克服纯滞后的一个有效控制方法[3]。设计的原理是与PID控制器并联一个补偿环节,用来补偿被控对象中的纯滞后部分。
RBF神经网络有很强的非线性拟合能力,可映射任意复制的非线性关系,而且具有学习算法简单、运算量小、收敛快等优点。利用RBF神经网络在线自学习整定PID参数,构成一个具有自调节能力、稳定的控制器。
为了满足系统的抗扰性、快速性、稳定性,提高控制质量,本文提出了一种基于Smith预估补偿与RBF神经网络模糊PID控制算法。
1 Smith预估补偿控制原理
针对纯滞后系统闭环特征方程含有影响系统控制品质的纯滞后问题,1957年Smith提出了一种预估补偿控制方案,即在PID反馈控制基础上引入一个预估补偿环节,使闭环特征方程不含有纯滞后项,以提高控制质量[4]。
在图1所示的单回路控制系统中,控制器的传递函数为D(s),被控对象传递函数为Gp(s)e-τs,被控对象中不包含纯滞后部分的传递函数为Gp(s),被控对象纯滞后部分的传递函数为e-τs。
图1所示系统的闭环传递函数为:
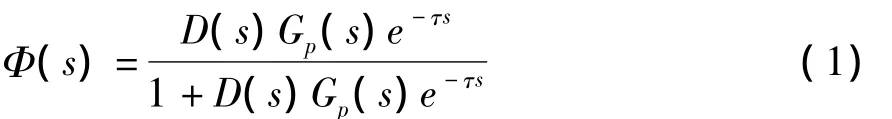
由式(1)可以看出,系统特征方程中含有纯滞后环节,它会降低系统的稳定性。如果能把图1中假想的变量N测量出来,那么就可以按照图2所示那样把N点信号反馈到控制器,这样就把纯滞后环节移到控制回路外边。
理想闭环系统结构示意图如图2所示。由图2可以得出闭环传递函数为:
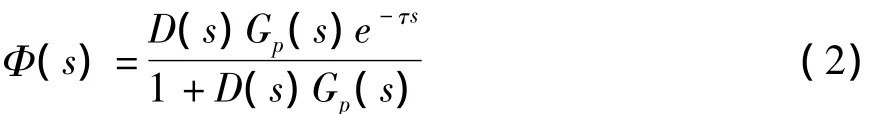
由上式可见,由于反馈信号N没有延迟,闭环特征方程中不含有纯滞后项,所以系统的响应将会大大改善。但是在实际情况中,脚踏板调速系统是大滞后系统,在N点将会出现负荷扰动,所以这种方案是无法实现的。

图1 纯滞后系统结构示意图Fig.1 Pure lag system structure diagram
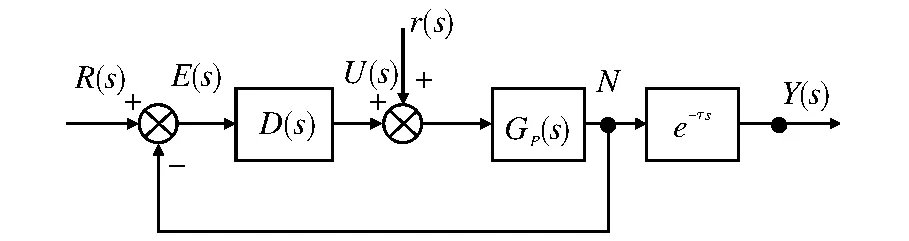
图2 理想闭环系统结构示意图Fig.2 Ideal closed - loop system structure diagram
实际工程上设计Smith预估器是在PID控制器中引入预估补偿器DC(s),其原理是将其并联在控制器D(s)上。如图3所示。其传递函数为:
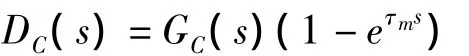
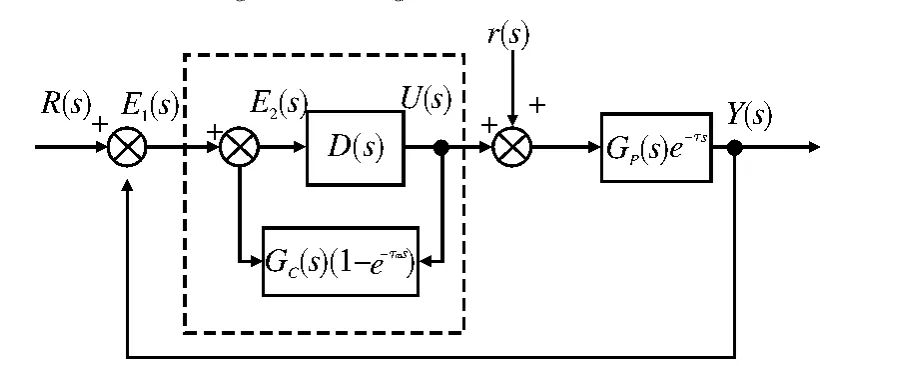
图3 Sm ith预估补偿控制系统框图Fig.3 Smith forecast compensation control system block diagram
图中虚线部分是带纯滞后补偿控制的控制器,其传递函数为:
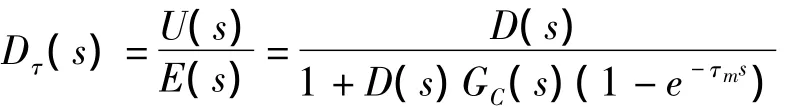
如果模型精确,可令GC(s)=GP(s),τm=τ且不存在负荷扰动,r(s)=0.
经过纯滞后补偿控制后系统的闭环传递函数为:
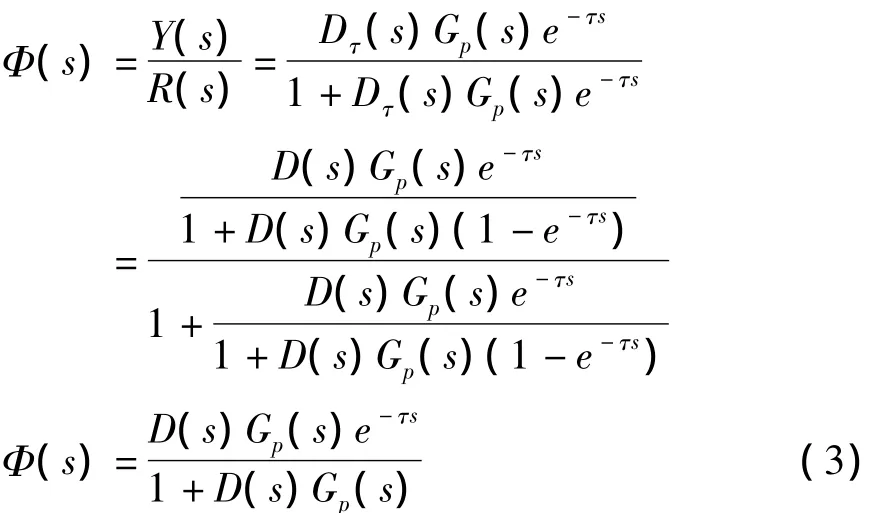
由式(3)可见,带纯滞后补偿的闭环系统与图2所示的理想结构是一致的,其特征方程为:1+D(s)Gp(s)=0。经补偿后 ,实现了将纯滞后环节移到闭环控制回路之外,纯滞后环节e-τs已经不出现在分母中,从而有效消除了纯滞后对控制系统的影响。由此可知,使用Smith控制方法建立精确的预估模型需要知道被控对象的数学模型[4]。
2 RBF神经网络的PID整定
神经网络有很强的非线性拟合能力,可映射任意复杂的非线性关系,而且学习规则简单,便于实现。可以克服Smith控制方法必须确切地知道被控对象的数学模型的缺点。本文采用的RBF神经网络的PID算法,是一种鲁棒性强、控制精度高的控制方法。它主要包括两个部分:一是采用增量式PID的控制算法;二是利用神经网络对Jacobian矩阵(信息)进行辨识[5]。
2.1 RBF神经网络算法
RBF神经网络是一种性能优良的三层前馈型神经网络,由输入到输出的映射是非线性的,而隐含层空间到输出空间的映射是非线性的,从而大大加快了学习速度并避免局部极小值问题。RBF网络结构如图4所示。

图4 RBF神经网络结构示意图Fig.4 RBF neural network structure diagram
在 RBF 网络结构中,X=[x1,x2,…,xn]T为网络的输入向量。设RBF网络的径向基向量H=[h1,h2,…,hj,…,hm]T,其中hj为高斯基函数:
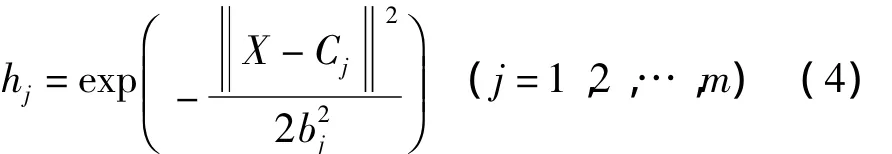
网络的第j个结点的中心矢量为Cj=[cj1,cj2,…,cji,…,cjn],其中,i=1,2,…,n。
设网络的基宽向量为:B=[b1,b2,…,bn]T,bj为节点j的基宽度参数且大于零。网络的权向量为:
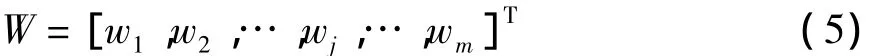
辨识网络的输出为:
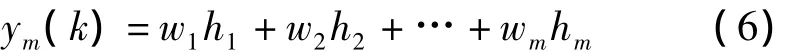
辨识器的性能指标函数为:
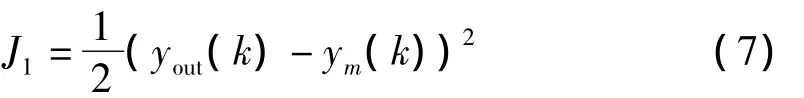
根据梯度下降法,输出权、节点中心及节点基宽参数的迭代算法如下:
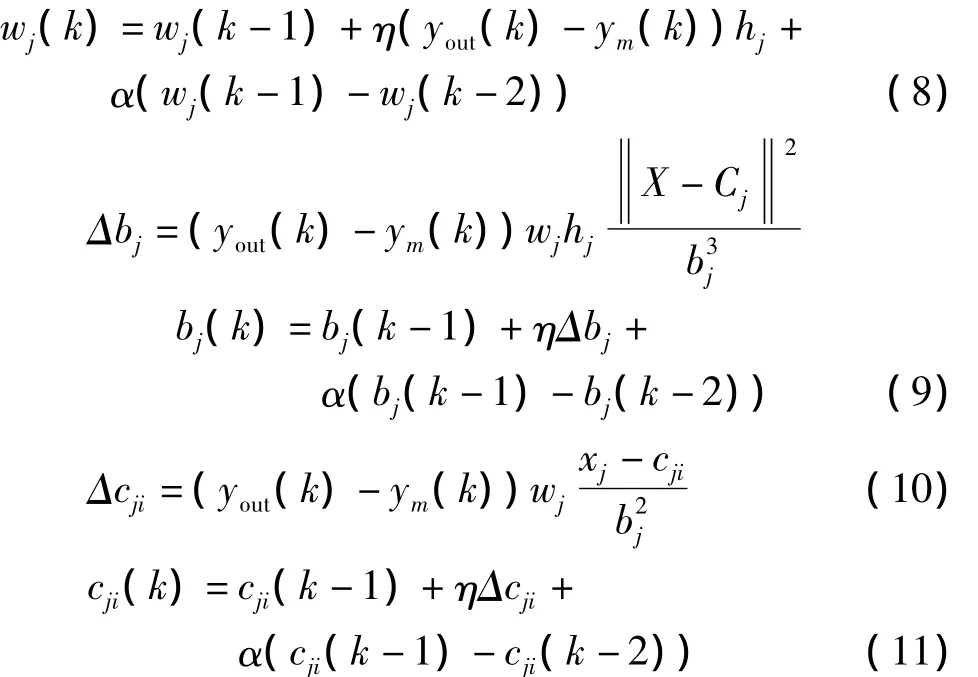
其中,η为学习速率,α为动量因子。
Jacobian矩阵(即为对象的输出对控制输入变化的灵敏度信息)算法为:
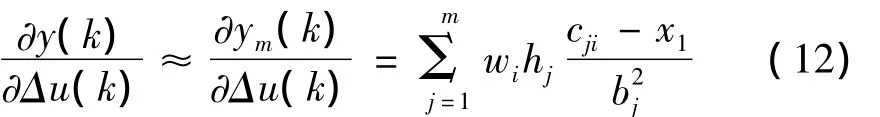
式中,x1=Δu(k)。
2.2 RBF网络PID整定原理
RBF网整定PID控制参数采用增量式PID控制器,控制误差为:

神经元PID控制器的三项输入为:

控制算法为:
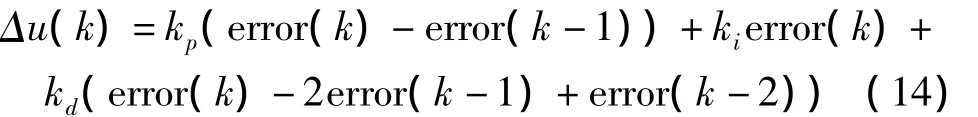
神经网络整定指标为:

kp,ki,kd的调整采用梯度下降法:
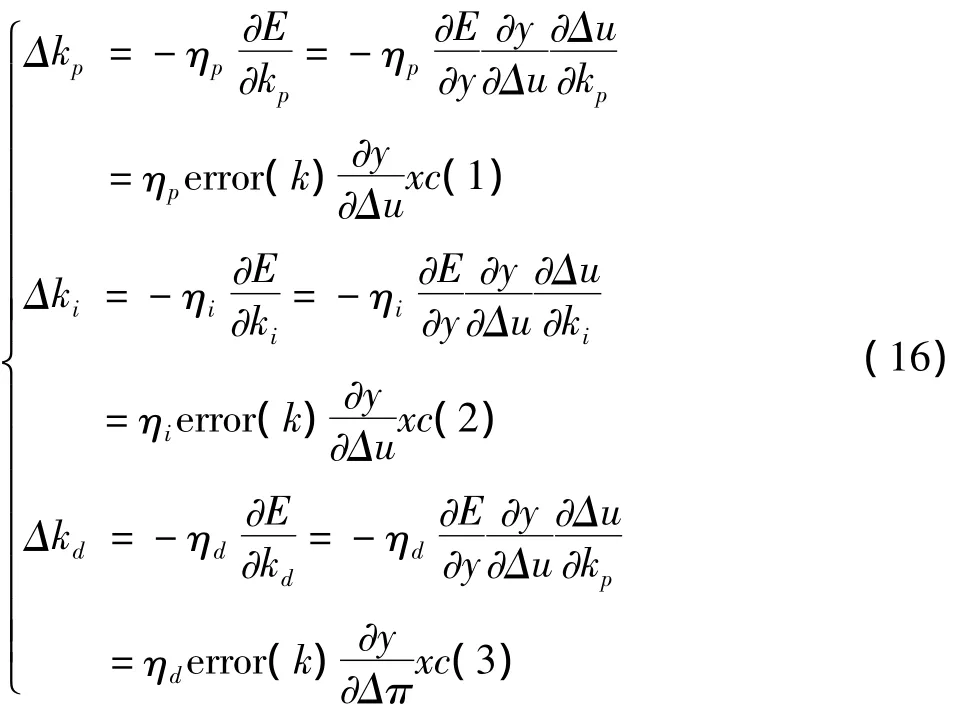
式中,ηp,ηi,ηd分别为比例、积分、微分的学习速率为被控对象的Jacobian信息,可通过神经网络的辨识而得[6]。
RBF整定PID控制系统结构图如图5所示。

图5 RBF网络整定PID控制框图Fig.5 RBF network setting PID control block diagram
3 基于Smith预估补偿与RBF神经网络PID控制算法及仿真结果
3.1 Smith预估补偿与RBF神经网络PID控制算法
Smith预估补偿与RBF神经网络PID控制结构图如图6所示。利用RBF神经网络不依赖于控制对象的精确模型的优点和在线学习方法,利用Smith预估补偿器对纯滞后系统的良好控制,以及利用PID控制能在小偏差范围内实现精确控制,达到优势互补的作用。
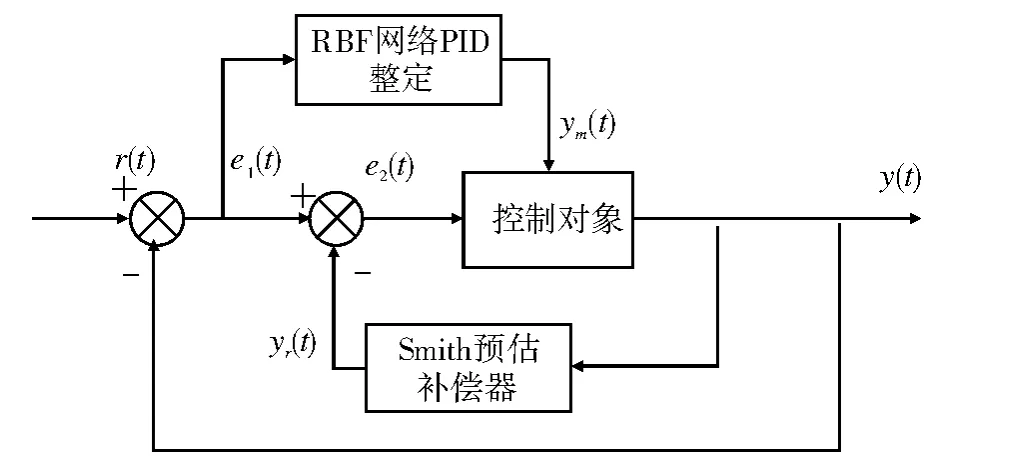
图6 Sm ith预估补偿与RBF神经网络模糊PID控制框图Fig.6 Smith forecast compensation and fuzzy RBF neural network PID control block diagram
3.2 仿真研究
本文研究的对象是平缝机调速模块的伺服系统,该系统可以用带有纯滞后的一阶模型模拟,控制对象为:Gp(s)=,采样时间为20 s,输入信号为方波响应。RBF的结构为3-6-1,网络辨识的3个输入为 rinm(k)=[Δu(k),yout(k),yout(k-1)],输出youtm(k)。用MATLAB 7.0进行仿真,控制器的仿真结果分别如图7-图10所示。
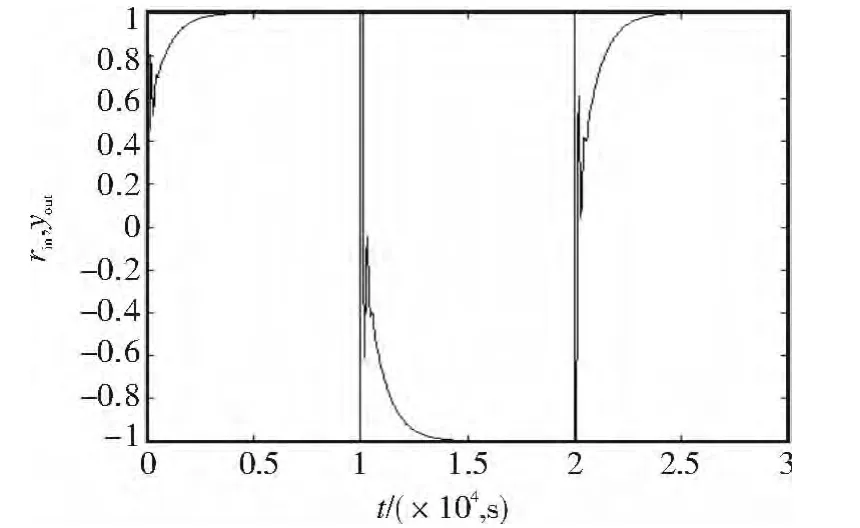
图7 PID控制的方波响应Fig.7 Square wave response of PID control

图8 精确模型Sm ith-PID控制的方波响应Fig.8 Precise Smith - square wave response of the PID controlmodel
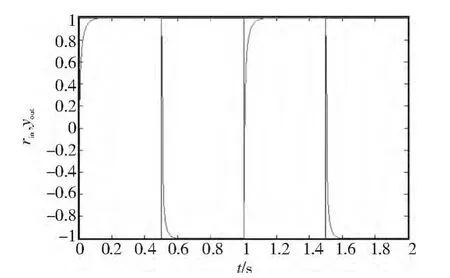
图9 RBF-Sm ith-PID控制的方波响应Fig.9 RBF-Smith-PID control square wave response
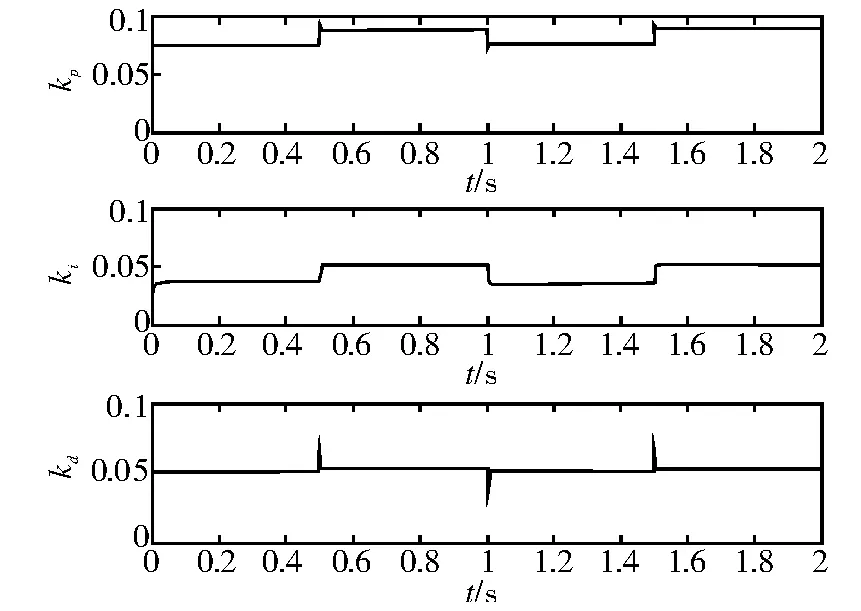
图10 RBF-Sm ith-PID控制参数自适应整定曲线Fig.10 RBF-Smith-adaptive PID control parameters setting curve
3.3 仿真结果分析
根据仿真结果可见,采用纯PID控制,当外界存在扰动时,系统具有较大的超调量,平缝机调速模块的控制精度变差,现场试验时会出现抖动现象;当采用精确模型Smith-PID控制时,系统超调量减小,控制效果显著增强;当采用RBF-Smith-PID控制时,从图10可知控制参数可以在线整定,系统稳定度和精度高,在进行无级调速时,速度变化平滑,停针和启针的精度都在要求范围之类,控制系统更加优越。
4 结论
本文针对平缝机调速模块的伺服系统是一个多变量、非线性、强藕合、大滞后系统,提出了基于Smith预估补偿与RBF神经网络PID控制算法。该算法利用各算法的优点和互补性,经过理论分析和仿真表明,该算法很好改善了传统PID在控制过程中不能克服非线性因素的影响、对调节对象的参数不能在线整定等缺点,使该系统调速平滑,具有良好速度跟随性。
[1]姜建奎.工业平缝机控制器的研究[D],中南大学,2009.
[2]楼彦华.基于DSP的全自动直驱工业缝纫机控制系统研究[D].浙江大学,2010.
[3]唐彪.基于模糊PID的Smith预估控制器[D].中南大学,2010.
[4]王宝忠,宋东锋.基于Smith预估补偿与RBF神经网络的改进PID控制[J],现代电子技术,2011,34(5):161-165.
[5]飞思科技产品研发中心.神经网络理论与MATLAB7实现[M].北京:电子工业出版社,2002.18-23.
[6]刘金琨.先进 PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003.104 -111.

