铁路悬索桥纵向非一致激励地震响应分析

杨海洋，钟铁毅，夏 禾

（北京交通大学土木建筑工程学院，北京 100044）

铁路悬索桥纵向非一致激励地震响应分析

杨海洋，钟铁毅，夏 禾

（北京交通大学土木建筑工程学院，北京 100044）

以某三跨铁路悬索桥为例，基于大型通用有限元软件ANSYS，采用行波输入与多点激励两种非一致地震激励进行铁路悬索桥地震响应计算分析。研究获得大跨度悬索桥在非一致激励输入下响应变化规律，并通过分析桥梁各响应控制振型变化获得非一致激励对桥梁地震响应影响机理，从而揭示两种非一致激励考虑方式对桥梁响应影响的根本区别，为悬索桥非一致激励下地震响应计算分析提供重要参考依据。

悬索桥；非一致激励；控制振型；行波效应；多点激励

大跨度桥梁的抗震性能已受到高度重视，并有大量研究［1－4］。对其分析过程中关键为确定地震动输入。地震动本质为空间变化，由于桥梁跨度大、基底延伸长，地基各点振幅、相位差别较大，考虑地震动多点非一致输入极为重要［5］。

Abdel-Ghaffar等［6］利用实际地震记录分别在时、频域内对金门大桥进行地震反应分析。结果表明，一致输入反应分析并非代表最不利情况，行波效应对悬索桥的地震反应影响显著。Nakamura等［7］用多点激励反应谱方法对金门大桥进行分析，认为受其柔性影响，以动力反应分量为主，行波效应及多点激励对动力反应分量影响显著，且多点激励会致桥塔有小响应。Dumanoglu等［8］对三座欧洲大跨度箱梁悬索桥行波效应比较分析发现，在悬索桥的某些部位行波效应会增大地震反应。Harichandran等［9］认为对悬索桥进行一致输入分析会高估某些部位反应，低估其它部位反应。胡世德等［10］通过对江阴长江大桥地震反应分析，认为行波效应会使结构反应增大，而多点激振影响较小。郭发忠［11］通过对某三跨悬索桥的地震响应分析，认为由于多支承激励引起的柔性结构地震反应中拟静力部分占比较小，总体上行波效应对结构内力反应影响不大。有研究［12－14］只考虑行波效应或直接生成人工地震波，虽用两种方案进行计算，但均未能揭示两种非一致激励考虑方式对桥梁响应影响的根本区别。只考虑行波效应会高估各点间相关性，直接生成人工地震波而不进行谱拟合则会致生成的人工地震波反应谱值与实际地震波不符，如长周期段谱值偏小等，且各点间地震波反应谱值差异亦会造成桥梁地震响应变化。

本文以某三跨铁路悬索桥为例，基于大型通用有限元软件ANSYS采用行波输入与多点激励两种非一致地震激励对铁路悬索桥进行地震响应计算分析，获得该桥的响应变化规律。对归一化后桥梁地震响应时程进行傅里叶变换并分析谱值，获得桥梁各响应控制振型变化，给出非一致激励对桥梁地震响应影响机理，揭示两种非一致激励考虑方式对桥梁响应产生影响的根本区别。

1 多点人工地震波生成

将各点随机相位角项φmk设为一致，即与各点位置无关φk，便得局部场地收敛的多点地震波［15］。进行反应谱拟合时，本文采用考虑相位谱的人造地震动反应谱拟合方法［16］，可得合理的加速度时程曲线，但会在模拟所得地震地面运动中引入长周期分量，造成直接积分的速度、位移时程曲线严重失真。本文通过时域内基线调整及频域内过滤掉不合理长周期分量方法达到零线调整目的。本文加速度时程与某组地震波位移时程对比见图1。由图1看出，考虑多点相关性多点激励输入的各支承点位移时程较接近，无明显延后现象。

图1 本文生成的加速度时程及各点位移时程示例Fig．1 Acceleration time history and disp lacement time histories

2 计算模型及自振特性分析

本文以拟建某特大铁路悬索桥为计算分析模型，用ANSYS有限元分析软件建模。桥梁为地锚式悬索桥，跨度98 m＋660 m＋98 m，中跨设置吊杆，在跨中设置三对柔性中央扣，边跨无吊杆，主塔为混凝土，高196 m、156 m，主梁用上承式钢桁梁，桥面宽24 m，桁高12 m。主桁与桥塔横梁相交处只设竖向、横桥向支座，顺桥向无约束，主梁两端只约束竖向、横桥向位移。悬索桥立面图及各支承点编号见图2。

图2 悬索桥立面图Fig．2 Elevation of the suspension bridge

为简化计算、明确主梁内力变化，桥梁有限元模型用鱼骨式建模，见图3。桥梁前10阶振型及描述见表1。桥梁前10阶振型见图4。设置柔性中央扣后桥梁纵飘振型出现被延后，桥梁1阶振型为主梁对称横弯。桥梁周期较长，表明该桥属柔性结构。应对桥梁内力、位移进行分析研究。

图3 ANSYS有限元模型Fig．3 ANSYS finite elementmodel of full-bridge

表1 前10阶振型及描述Tab.1 Top 10 vibration modes of the bridge

图4 前10阶振型图Fig．4 Top 10 vibration shape diagram

3 非一致激励下桥梁地震响应分析

本文将系统对大跨度悬索桥在两种不同非一致激励方式下地震响应进行分析。为反映不同输入对桥梁地震响应统计意义的变化规律，生成5组多点地震波进行计算，每组地震波含3种波速，分别为500 m／s、1000 m／s及2 000 m／s，每种波速下均含悬索桥的6个支承点地震波。计算一致激励时用多点输入的第1点地震波计算，行波输入则对第1点地震波做延时处理，以保证几种输入方式的可比性。采用常遇地震顺桥向加载，按50年超越概率63%计算，加速度峰值为0．79 m／s2，计算中考虑几何非线性影响，并设地震波从左向右传播。计算结果均为用5组地震波分别计算平均值，且均为与自重荷载组合结果。分析主梁位移时为相对主梁左端相对位移，分析桥塔位移时则为相对各塔底相对位移。

3.1 主缆及吊杆

5组地震波作用、不同输入方式下主缆及吊杆应力平均值见图5。由表2看出，随波速变化不同非一致激励方式下地震响应均有不同。行波输入下随波速减小主缆及吊杆最大应力均有增大，但幅度较小，主缆应力最大增大4．82%，吊杆最大应力最大增加3．12%；多点激励作用下主缆及吊杆应力与一致输入基本一致，幅值变化约1%。考虑本文加载地震动峰值较小，地震造成的响应与自重下内力相比较小，按罕遇地震加载时各响应浮动百分比应增大。多种工况作用下吊杆最小应力为0值时出现于跨中正中部位，表明地震作用下该位置吊杆可能出现松弛，设计时应采取必要构造措施。不同输入方式的吊杆应力随吊杆位置分布见图5。由图5看出，两种非一致输入方式的吊杆应力分布与一致激励基本一致，仅应力幅值有区别。

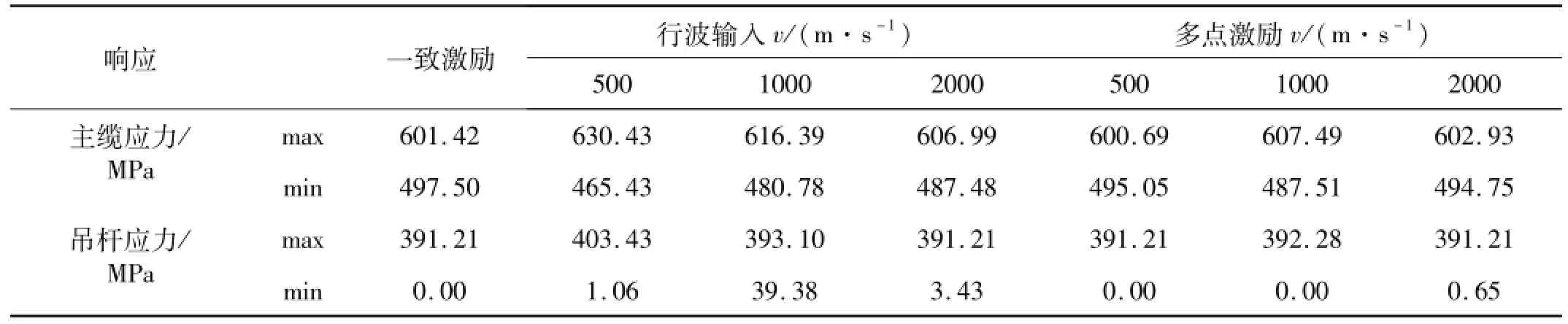
表2 主缆及吊杆应力Tab.2 Stress of main cable and suspender

3.2 主梁

不同输入下的主梁最大地震响应见表3。由表3看出，行波输入下，随波速的减小主梁最大竖向位移、弯矩及剪力均呈增长趋势，波速500m／s时增幅分别为403．03%、10．88%及4．37%；而梁端顺桥向位移及主梁最大轴力变化规律不明显，除波速1 000 m／s有所减小外基本与一致激励持平，且梁端顺桥向位移有减小趋势；多点激励作用下仅主梁竖向位移有所增长，波速1 000 m／s时增长100%，但总体随波速变化规律不明显；而梁端位移、主梁最大轴力、最大竖向弯矩及剪力亦与一致激励基本持平。

为进一步研究两种不同非一致输入下主梁的响应变化规律，主梁竖向位移、主梁轴力、主梁竖向弯矩及主梁竖向剪力沿梁长包络见图6～图9。由4图看出，不同输入下主梁响应发生变化区域均为中跨，两侧边跨响应基本无影响。行波输入下主梁跨中竖向位移显著增大，包络形状由一致激励的中跨1／4跨、3／4跨双峰变为1／2跨单峰，跨中弯矩明显增大，剪力变化不明显。多点激励输入下主梁跨中竖向位移有一定程度增长，但包络仍为双峰形式，主梁竖向弯矩、剪力包络无明显变化。两种输入下主梁轴力分布均与一致激励相同，区别仅在于峰值大小。因此，两种输入方式对主梁响应有较大不同，考虑非一致激励影响时应谨慎选则。

表3 主梁最大地震响应Tab.3 Maximum of seism ic responses ofmain girdle

图5 吊杆应力分布Fig．5 Distribution of suspension stress

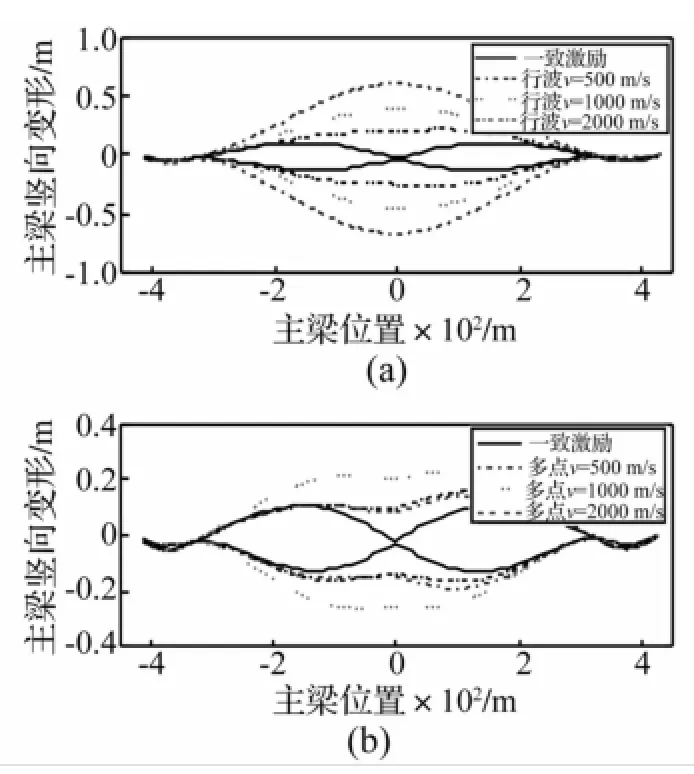
图6 主梁竖向位移包络Fig．6 Vertical displacement envelope ofmain girdle

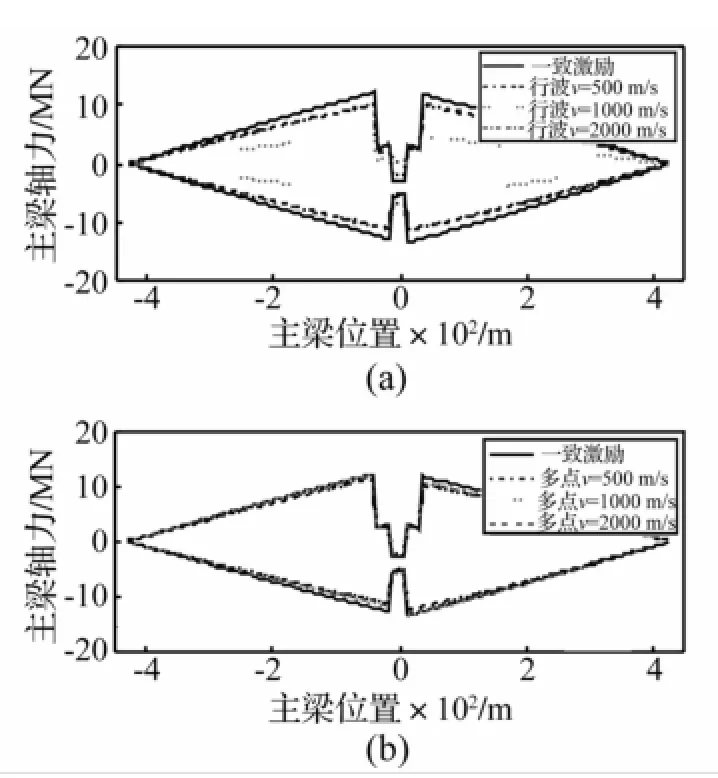
图7 主梁轴力包络Fig．7 Axial force envelope ofmain gird le

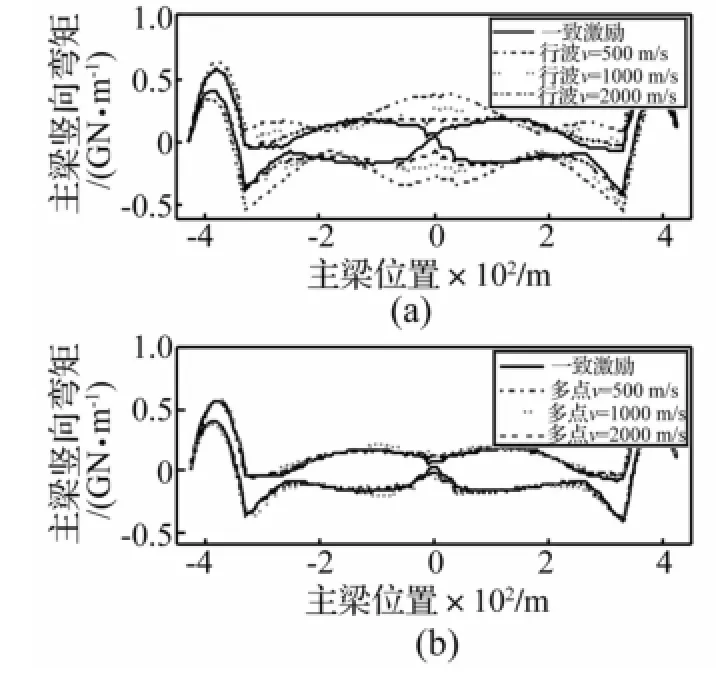
图8 主梁竖向弯矩包络Fig．8 Verticalmoment envelope ofmain girdle

图9 主梁竖向剪力包络Fig．9 Vertical shearing force envelope ofmain girdle

图10 主梁端部顺桥向位移傅里叶幅值谱Fig．10 Amplitude spectra of longitudinal displacement ofmain girdle

为进一步分析桥梁在非一致激励作用下响应变化机理，本文对主梁各位置响应时程归一化的傅里叶幅值谱计算分析。图10为两种非一致激励对主梁响应影响机理区别的端部顺桥向位移幅值谱。由图10看出，行波输入下各响应幅值谱在频率点0．253 Hz处谱值均出现不同程度增长，且随波速减小而加深，而多点激励作用下未见类似情况。0．253 Hz处为主梁一阶竖弯振型，其形状与行波500m／s的主梁竖向位移包络一致。

3.3 桥塔

不同输入方式下两侧桥塔最大顺桥向地震响应见表4。由表4看出，行波输入下桥塔最大顺桥向位移与塔底轴力均有所增加，其中矮塔顺桥向位移增加107．28%，塔底轴力增加2．87%，而塔底弯矩及剪力幅值则略有减小，最大减幅分别达27．21%及26．48%，但随波速增大各项响应均越接近一致激励结果；多点激励作用下各项地震响应均基本与一致激励持平，无明显变化规律。

表4 桥塔最大顺桥向地震响应Tab.4 Maxim um of longitudinal seism ic responses of towers

图11～图14为桥塔顺桥向位移、轴力、顺桥向弯矩及顺桥向剪力包络，由于包络线基本对称，仅给出一侧。由4图看出，不同输入下，桥塔顺桥向位移包络发生明显变化：一致输入时桥塔最大顺桥向位移发生于塔梁固结处与塔顶间桥塔中部，考虑非一致激励后塔顶顺桥向位移均不同程度增大，矮塔更明显。桥塔轴力包络无明显区别，仅幅值有所区别。桥塔顺桥向弯矩（剪力）包络在波速500 m／s时变化较大，并仍以矮塔明显。此矮塔支承点输入地震波延时较长，且矮塔自振周期较高塔短的缘故。

图11 桥塔顺桥向位移包络Fig．11 Longitudinal displacement envelope of tower

图12 桥塔轴力包络Fig．12 Axial force envelope of tower

图13 桥塔顺桥向弯矩包络Fig．13 Longitudinalmoment envelope of tower

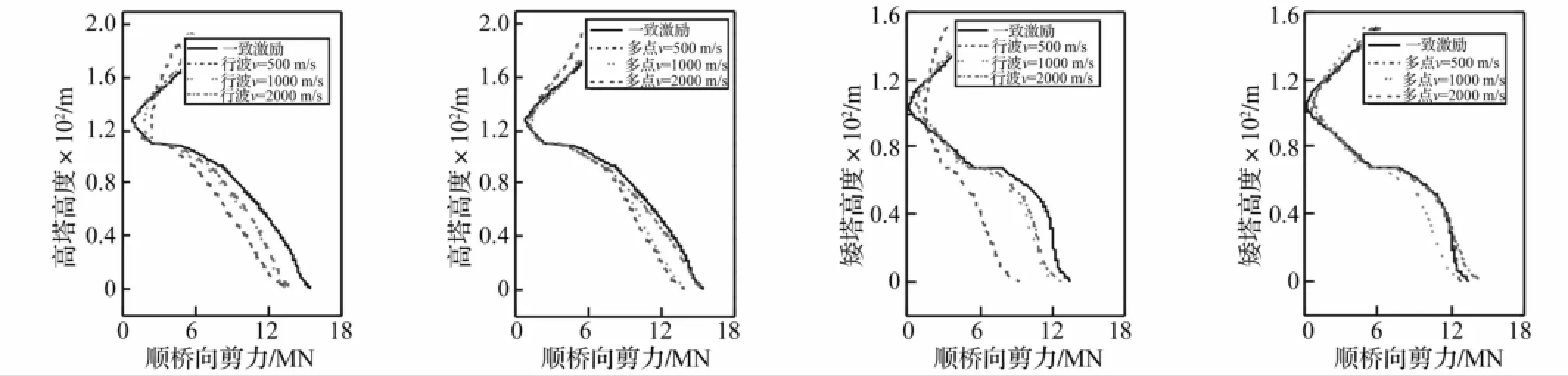
图14 桥塔顺桥向剪力包络Fig．14 Longitudinal shearing force envelope of towe

对桥塔各项地震响应傅里叶幅值谱进行分析。矮塔塔底顺桥向弯矩幅值谱见图15。由图15看出，该结果与主梁分析结果一致，桥塔地震响应幅值谱仍为行波输入下0．253 Hz处幅值增加，而多点激励作用下则无明显变化。结果表明，行波输入对大跨度悬索桥影响主要表现为对一阶竖向振型激发，且能使该振型成为部分响应的控制振型，多点激励对主要振型无显著影响。其原因为行波输入下各点间相对位移较大，拟静力位移导致桥梁一阶振型激发，多点激励因各点间位移时程相差较小，故无此现象产生。

图15 矮塔塔底顺桥向弯矩傅里叶幅值谱Fig．15 Amplitude spectra of longitudinalmoment of tower

4 结 论

本文结合某大跨度铁路悬索桥，基于大型有限元通用软件ANSYS，进行两种非一致激励下地震动响应分析，结论如下：

（1）行波输入下桥梁主缆及吊杆应力随波速减小而增加，而多点激励作用下，主缆及吊杆应力与一致输入基本相同。两种输入方式下，吊杆应力分布与一致激励无明显区别。

（2）两种非一致激励作用时主梁竖向位移较一致激励均有所增大，行波输入时增大更显著，且随波速减小增幅增大，并伴随主梁竖向弯矩、位移包络形状改变；多点输入作用时主梁竖向位移随波速变化规律不明显，竖向弯矩、位移包络无明显改变。两种非一致激励作用时主梁竖向剪力峰值及包络变化不明显。

（3）行波输入时桥塔最大顺桥向位移与塔底轴力均有所增大。而塔底弯矩及剪力幅值则略有减小，但波速越快各项响应越接近一致激励结果；多点激励作用下各项地震响应均与一致激励基本持平，无明显变化规律。两种非一致激励作用时塔顶位移均显著增大。

（4）行波输入对大跨度悬索桥影响主要表现为对一阶竖向振型激发，而多点激励对主要控制振型无显著影响。各点间相对位移较大，拟静力位移致桥梁一阶振型激发，多点激励由于各点间位移时程相差较小。

（5）不同输入下悬索桥地震响应的主要控制振型未发生改变时其响应幅值变化不会太大。进行悬索桥地震响应分析前应先分析各响应主要控制振型，以便选择合理的地震动输入方式。

（6）本文计算结果仅考虑常遇地震，所得桥梁地震响应变化幅度仅作规律研究。罕遇地震作用下响应变化幅度会更明显，设计中应注意。

［1］李吉涛，杨庆山，刘阳冰．多点地震激励下大跨连续钢构桥易损性分析［J］．振动与冲击，2013，32（5）：75－80．

LIJi-tao，YANG Qing-shan，LIU Yang-bing．Fragility analysis of long span continuous rigid frame bridge undermulti-support excitations［J］．Journal of Vibration and Shock，2013，32（5）：75－80．

［2］柳国环，李宏男，田利．九江长江大桥在多点多维地震激励下的反应分析［J］．振动与冲击，2009，28（9）：224－230．

LIU Guo-huan，LIHong-nan，TIAN Li．Response analysis of Jiujiang Yangtze river highway bridge under spatially variable earthquake ground motions［J］．Journal of Vibration and Shock，2009，28（9）：224－230．

［3］Lin JH，Zhang Y H，Li Q S，et al．Seism ic spatial effects for long-span bridges using the pseudo excitation method［J］Engineering Structures，2004，26（9）：1207－1216．

［4］刘洪兵，朱晞．大跨度斜拉桥多支承激励地震响应分析［J］．土木工程学报，200l，34（6）：38－44．

LIU Hong-bin，ZHU Xi．Seismic response analysis of longspan cable-stayed bridges under multi-support excitations［J］．China Civil Engineering Journal，2001，34（6）：38－44．

［5］苗家武，胡世德，范立础．大型桥梁多点激励效应的研究现状与发展［J］．同济大学学报，1999，27（2）：189－123．

MIAO Jia-wu，HU Shi-de，FAN Li-chu．State of art and development of study on seismic performance of long span bridges under multiple-support excitations［J］．Journal of Tongji University，1999，27（2）：189－123．

［6］Abdel-Ghaffar A M，Rubin L I．Suspension bridge response to multiple-support excitations［J］．Journal of Engineering Mechanics，ASCE，1982，108（2）：419－435．

［7］Nakamura Y，Kiureghian A D，Liu D V．Multi-support response analysis of the golden gate bridge［R］．University of California atBerkely，Report No．UCB／EERC－93／05，1993．

［8］Dumanoglu A A，Brownjohn JMW，Severn R T．Seismic analysis of the fatih sultan mehmet suspension bridge［J］．Earthquake Engineering and Strutural Dynamics，1992，21：881－906．

［9］Harichandran R S，Hawwari A，Sweidan B N．Response of long-span bridges to spacially varying ground motion［J］．Journal of Structural Engineering ASCE，1996，122（5）：476－484．

［10］胡世德，范立础．江阴长江公路大桥纵向地震反应分析［J］．同济大学学报，1994，22（4）：433－438．

HU Shi-de，FAN Li-chu．The longitudinal earthquake response analysis for the Jiangyin Yangtze river bridge［J］．Journal of Tongji University，1994，22（4）：433－438．

［11］郭发忠．大跨度悬索桥行波激励地震反应分析［J］．公路交通技术，2011（3）：60－62．

GUO Fa-zhong．Analysis for seisimic response of traveling wave excitation of large-span suspension bridges［J］．Technology of Highway and Transport，2011（3）：60－62．

［12］张卉，王志清，彭元诚，等，四渡河大跨悬索桥空间地震响应分析［J］．地震工程与振动，2007，27（3）：70－76．

ZHANG Hui，WANG Zhi-qing，PENG Yuan-cheng，et al．Spatial seismic response analysis of long-span suspension bridge across Sidu river［J］．Earthquake Engineering and Engineering Vibration，2007，27（3）：70－76．

［13］孙永涛．大跨悬索桥在多点激励作用下的地震反应分析［D］．哈尔滨：哈尔滨工业大学，2009．

［14］陈海波．大跨度悬索桥的地震反应分析［D］．合肥：合肥工业大学，2010．

［15］董汝博，周晶，冯新．一种考虑局部场地收敛性的多点点地震动合成方法［J］．振动与冲击，2007，26（4）：5－9．

DONG Ru-bo，ZHOU Jing，FENG Xin．A local convergent method for simulating multi-point earthquake ground motion［J］．Journal of Vibration and Shock，2007，26（4）：5－9．

［16］胡聿贤，何训．考虑相位谱的人造地震动反应谱拟合［J］．地震工程与工程振动，1986，6（2）：37－51．

HU Yu-xian，HE Xun．Phase angle consideration in generating response spectrum-compatible groundmotion［J］．Journal of Earthquake Engineering and Engineering Vibration，1986，6（2）：37－51．

Seism ic responses analysis of a railway suspension bridge under longitudinal non-uniform excitations

YANGHai-yang，ZHONG Tie-yi，XIAHe
（School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China）

Based on the general finite element software ANSYS，seismic responses under non-uniform excitations of a long-span railway suspension bridge were studied．Two different inputmethods，i．e．，traveling seismic wave excitation and multi-support excitation，were used to analyze the seismic responses of the bridge，and then the response regulations were discussed．Analysing the differences between the response control modes，the influence mechanisms of the nonuniform excitations were discussed，thus the fundamental differences between effects of the two input methods were revealed．The results can provide an important basis for the seismic analysis of suspension bridges．

suspension bridge；non-uniform excitation；controlmode；travelling wave effect；multi-support excitation

U24

：A

10．13465／j．cnki．jvs．2014．22．028

铁道部科技研究开发计划（2010G004－I）；国家重点研究计划“973”项目（2013CBO36203）

2013－11－08 修改稿收到日期：2014－01－15

杨海洋男，博士生，1991年6月生

钟铁毅男，博士后，副教授，1963年4月生