基于H ilbert-Huang变换的切削颤振识别

贾广飞，吴 波，胡友民

（1．华中科技大学数字制造装备与技术国家重点实验室，武汉 430074；2．河北科技大学机械工程学院，石家庄 050018）

基于H ilbert-Huang变换的切削颤振识别

贾广飞1，2，吴 波1，胡友民1

（1．华中科技大学数字制造装备与技术国家重点实验室，武汉 430074；2．河北科技大学机械工程学院，石家庄 050018）

针对切削颤振信号的非线性、非平稳特征，提出基于Hilbert-Huang变换的切削颤振识别方法。通过对颤振信号进行经验模态分解（EMD）获得一系列本征模函数，筛选出对颤振敏感的本征模函数进行带通滤波，对滤波后本征模函数作Hilbert变换，绘制Hilbert谱；提取Hilbert谱幅值标准差进行颤振定量识别。用仿真及实测振动信号验证该方法的有效性，并用小波包分解方法进行对比。

Hilbert-Huang变换；切削颤振；经验模态分解（EMD）

切削颤振为金属切削过程中刀具与工件间的强烈自激振动。其危害包括降低表面质量及精度、加剧刀具磨损或破损、产生较大噪声及降低生产效率等［1－2］。随高速高精加工及难加工材料加工发展，切削颤振已成为制约生产效率、提高表面质量之瓶颈。因此对切削颤振研究具有重要的现实意义。

切削颤振研究主要分颤振机理与动力学建模研究及颤振在线监测与抑制研究两类。由于颤振的产生涉及机床本体、刀具装夹、工件材料及形状、切削参数等多种因素，较难建立精确动力学模型。颤振监测信号分析为提取有效颤振特征量与颤振识别的关键。对颤振信号进行时域分析为最直接、常用方法。王太勇等［3］基于车削过程中刀具磨损声信号、振动信号的时域统计参数分析、相关分析及AR分析建立三级颤振判断模式，发现颤振频率，找出颤振根源。Tangjitsitcharoen［4］用动态切削力功率谱密度识别颤振，认为对颤振信号分析时兼顾时频域特征更全面更可靠。Kuljanic等［5］用多传感器信号的小波变换提取颤振特征，用神经网络进行颤振识别。尽管小波变换时频分辨率较好，但由于小波基函数需预先选定，故信号分解并非自适应。Huang等［6］提出的基于数据自身特性的自适应分解信号时频方法，亦称Hilbert-Huang变换，在分析非线性、非平稳信号时具有突出优势。Hilbert-Huang变换在轴承［7］、齿轮［8］等旋转机械故障诊断中应用较多，但在切削颤振信号分析中应用较少。针对切削颤振信号具有的非线性、非平稳特征［9］，本文提出基于Hilbert-Huang变换进行切削颤振信号分析，提取颤振特征量进行颤振识别。仿真、实测信号验证该方法的有效性。

1 H ilbert-Huang变换基本原理

Hilbert-Huang变换含经验模态分解（EMD）与Hilbert谱分析（HSA）两部分。前者为Hilbert-Huang变换中创新内容，Hilbert谱分析目的为计算瞬时幅值、瞬时频率，绘制Hilbert谱。

1.1 经验模态分解（EMD）

为分析非线性、非平稳信号，设任何信号均由简单本征振荡模式组成。每个简单振荡模式称为一个本征模函数（IMF），须满足［10］：①在整个数据段，极值点个数与过零点个数须相等或最多相差一个；②在任何数据点由局部极大值点形成的上包络与由局部极小值点形成的下包络均值为零。由于实际信号不满足该条件，因此Huang等提出经验模态分解算法，步骤为：

（1）寻找信号x（t）的局部极大、极小值点；

（2）用三次样条曲线分别连接极大、极小值点形成上下包络线；

（3）由上下包络线的平均形成均值包络线m1（t）；

（4）寻找第一个本征模函数，计算残余：

通过经验模态分解，信号x（t）分解为n个IMF分量与一个残余分量rn（t）和的形式。

1.2 Hilbert谱分析（HSA）

每个IMF分量为近似单频率（或窄带）成分。分别对每个IMF作Hilbert变换，即

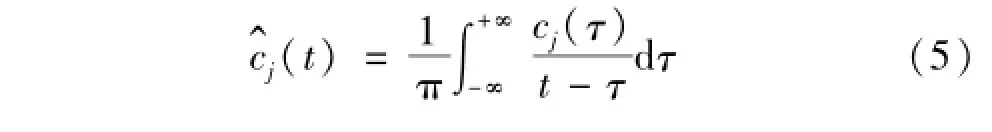
Hilbert谱可精确描述IMF分量幅值随时间、频率变化规律。

2 基于Hilbert-Huang变换的颤振识别流程

切削状态由平稳切削到颤振发展过程中振动信号会发生两种变化：①在时域，振动信号幅值在短时间内产生大波动且增大；②在频域，信号主频带发生转移且由宽变窄。因此对颤振信号进行时频域分析能更准确识别颤振。

基于Hilbert-Huang变换的颤振分析能将颤振信号自适应地分解成一系列近似单频率（或窄带）分量，通过Hilbert变换绘制Hilbert谱提取特征量进行颤振识别。为说明本方法优势，提供小波包分解加小波谱方法作对比。基于Hilbert-Huang变换的颤振识别步骤见图1。

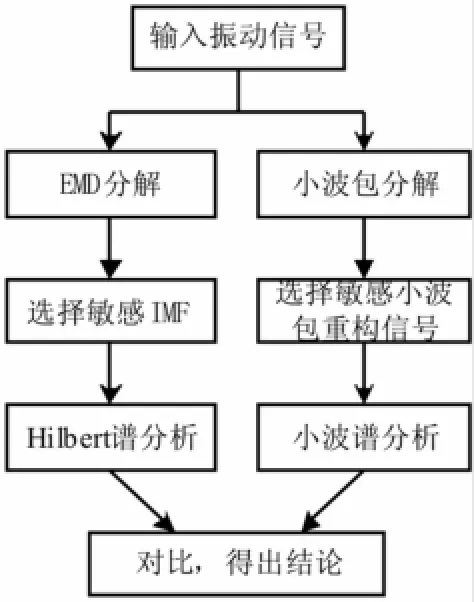
图1 Hilbert-Huang变换颤振识别流程Fig．1 The flow of chatter recognition based on Hilbert-Huang transform

3 仿真振动信号分析

为说明Hilbert-Huang变换分析含多分量振动信号优势，构造含高、低频成分及中频调频成分的复合仿真信号，表达式为

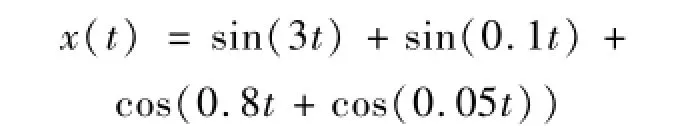
仿真信号时域波形、FFT幅值谱、小波时频谱及Hilbert谱见图2。由图2（b）看出，FFT幅值谱可清楚识别该仿真信号的频率成分，但缺乏时域信息，不能显示信号中调频成分；而图2（c）中小波谱具有较好时频分辨特征，能清晰显示信号中调频成分，但由于受时频不确定性影响，高频分量频率分辨率较低；图2（d）中Hilbert谱亦具有较好时频分辨特征，且较小波谱频率分辨率更高，高、低频频率分辨率一致。因此，利用Hilbert谱分析多分量振动信号具有明显优势。

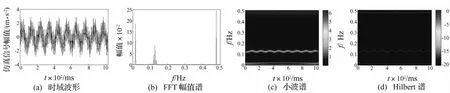
图2 仿真振动信号Fig．2 The simulated vibration signal

4 实测振动信号分析

为进一步检验本文方法在实测信号中的有效性，分析车削振动信号。立式数控车床（VL－850HR＋P）加工铝合金圆盘件时，用加速度传感器（PCB 356A15）采集车削振动信号，现场设备及传感器安装见图3。

图3 实验装置Fig．3 Experimental setup

实验中通过改变切削速度及切深采集振动信号。切削线速度150m／min、进给率0．1mm／r、切深0．5mm时，采集的振动信号见图4，采样频率10 kHz。由图4（a）看出，该信号时域幅值约在30 s后出现大幅波动且保持较大值，初步判断颤振发生；由图4（b）看出，在1 481 Hz处频率幅值最大。

对该信号作经验模态分解（EMD），提取颤振敏感分量。分解后前6个本征模函数及幅值谱见图5，其余本征模函数及残余分量因幅值较小，且与颤振分量相关度小未被显示。为对比，采用“db1”小波基、3层小波包分解结果见图6，图6（a）为各小波包重构波形，图6（b）为幅值谱。由图5看出，振动信号被自适应地分解为一系列本征模函数，且由上至下按频率从高到低排列。其中第二个本征模函数C2的时、频域幅值最大，且时域波形符合颤振特征，幅值谱频带近似单频率分量，被选为敏感IMF分量作下一步分析，也可采用相关系数法自动筛选敏感IMF分量［11］。经3层小波包分解，振动信号被分解为等带宽的8个小波包，该带宽与采样频率有关，并非据数据本身自适应分解。由图6看出，小波包［3，3］的时域幅值及频谱幅值均最大，被选为敏感小波包作下一步分析。对比图5、图6，敏感IMF幅值谱频带较敏感小波包频带更窄，频率分辨率更高。尽管小波包再作多层分解，也较难达到经验模态分解效果。

由于提取的敏感分量C2含较多噪声，先对其带通滤波后再进行Hilbert变换。绘制其Hilbert谱见图7。提取敏感小波包［3，3］绘制其连续小波谱见图8。对比图7（a）、图8看出，敏感分量Hilbert谱及小波谱均能较好反映信号的时频特征，但Hilbert谱较小波谱频率分辨率更高，能更好识别切削颤振现象。提取Hilbert谱幅值标准差为颤振特征量，可对颤振信号进行定量识别，敏感分量C2的瞬时幅值标准差曲线见图7（b）。通过设定标准差门限值，该颤振信号可分为三段，即平稳阶段（28～29．8 s）、过渡阶段（29．8～30．3 s）及颤振阶段（30．3～32 s），分别对应的标准差波动范围为0～0．3，0～0．7，0～1．2。

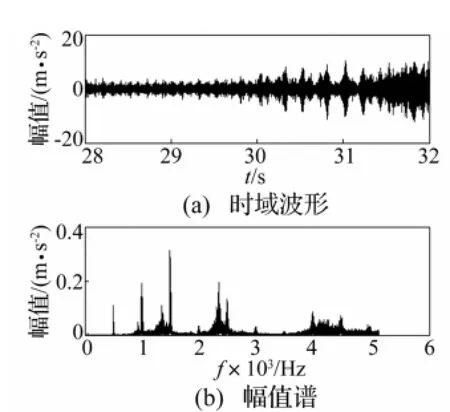
图4 车削振动信号Fig．4 A turning vibration signal

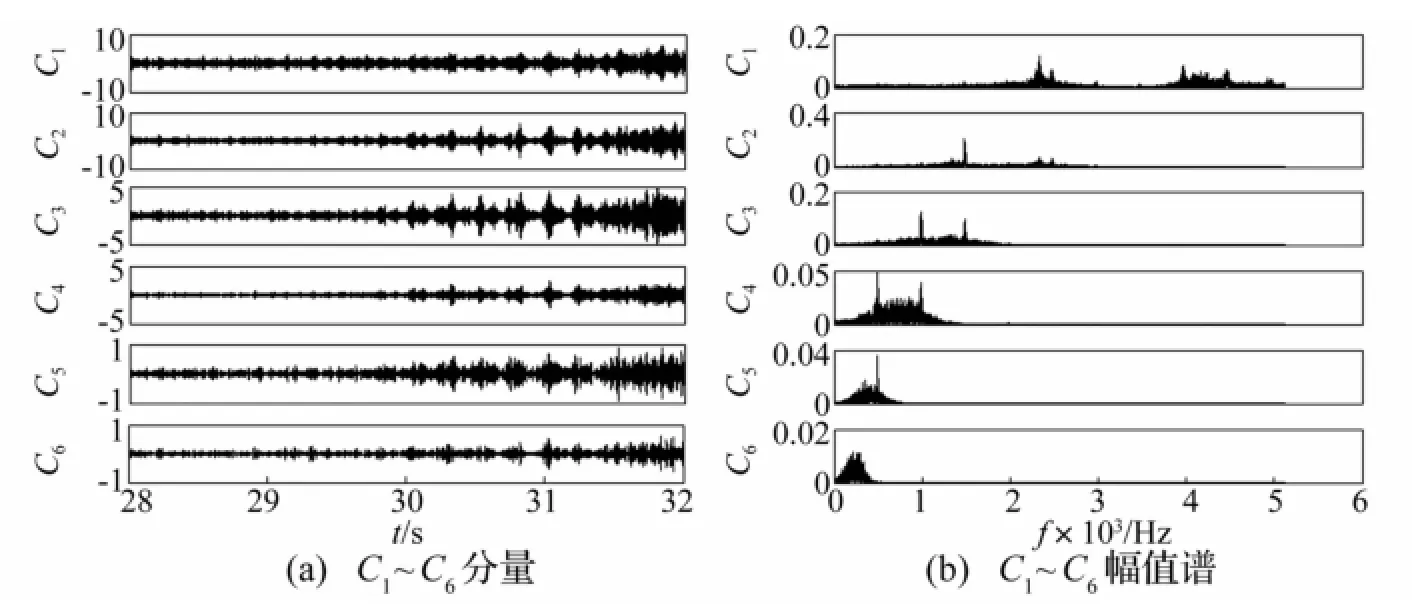
图5 车削振动信号经验模态分解Fig．5 EMD of a turning vibration signal

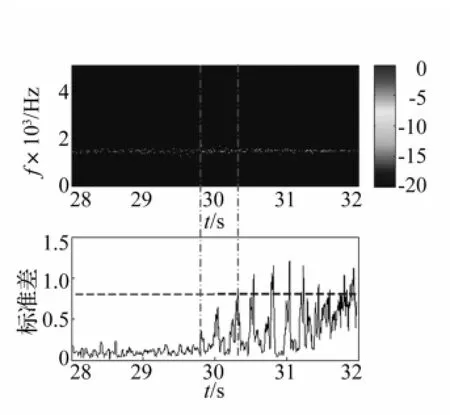
图7 敏感分量C2的Hilbert谱及标准差Fig．7 The Hilbert spectrum and standard deviation of sensitive component C2

图8 敏感小波包［3，3］的小波谱Fig．8 The wavelet spectrum of sensitive wavelet packet［3，3］

由此可见，通过对车削颤振信号进行经验模态分解、选取敏感IMF分量并对其作Hilbert变换、绘制Hilbert谱、提取该分量瞬时幅值标准差特征能定量识别切削颤振。

5 讨 论

尽管Hilbert-Huang变换方法在分析多分量、非线性、非平稳信号时优势明显，但由于该方法数学理论尚不完善，实际应用中存在模态混叠（图5）及计算效率低等问题。切削颤振信号为典型的非线性、非平稳信号，需在线识别。为解决模态混叠、计算效率低等问题，本文采用边采集、边分析的在线EMD颤振分析方法，将采样数据分成相等片段（如1 024），每片段作为一个窗口，取窗口的一个局部进行计算分析，且设定步长滑动分析，既能提高计算效率、减少模态混叠，亦适合对颤振数据的在线分析，已成功用于医学信号的在线分析［12］。

6 结 论

（1）针对切削颤振信号复杂的非线性、非平稳特征，本文提出的基于Hilbert-Huang变换的切削颤振识别方法通过对颤振信号进行经验模态分解，获得一系列本征模函数；对筛选出的敏感本征模函数作Hilbert变换、绘制Hilbert谱，提取瞬时幅值标准差作为特征量，实现颤振定量识别。

（2）本文方法较小波包分解及小波谱分析频率分辨率更高，亦能提高识别精度。

（3）为满足在线分析要求，提出的在线EMD颤振分析方法能提高计算效率、减少模态混叠。

［1］Wang L．Chatter detection and suppression using wavelet fuzzy control approaches in end milling［D］．Ottawa：University of Ottawa，Canada，2005．

［2］Quintana G，Ciurana J．Chatter in machining processes：a review［J］．International Journal of Machine Tools＆Manufacture，2011，51：363－376．

［3］王太勇，郭红旗，赵国立，等．刀具状态的声振多级在线监测模式研究［J］．机械工程学报，1995，31（6）：17－20．

WANG Tai-yong，GUO Hong-qi，ZHAO Guo-li，et al．Study on multi-level condition monitoring of cutting tool using acoustic and vibration signal［J］．Chinese Journal of Mechanical Engineering，1995，31（6）：17－20．

［4］Tangjitsitcharoen S．In-process monitoring and detection of chip formation and chatter for CNC turning［J］．Journal of Materials Processing Technology，2009，209：4682－4688．

［5］Kuljanic E，Totis G，Sortino M．Development of an intelligentmultisensor chatter detection system inmilling［J］．Mechanical Systemsand Signal Processing，2009，23：1704－1718．

［6］Huang N E，Shen Z，Long SR，et al．The empiricalmode decomposition method and the Hilbert spectrum for nonstationary time series analysis［J］．Proc．Roy．Soc．Lond．A，1998，454：903－995．

［7］苏文胜，王奉涛，张志新，等．EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用［J］．振动与冲击，2010，29（3）：18－21．

SU Wen-sheng，WANG Feng-tao，ZHANG Zhi-xin，et al．App lication of EMD de-noising and spectral kurtosis in early fault diagnosis of rolling element bearings［J］．Journal of Vibration and Shock，2010，29（3）：18－21．

［8］邵忍平，曹精明，李永龙．基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断［J］．振动与冲击，2012，31（8）：96－101．

SHAO Ren-ping，CAO Jing-ming，LI Yong-long．Gear fault pattern identification and diagnosis using time-frequency analysis and wavelet threshold de-noising based on EMD［J］．Journal of Vibration and Shock，2012，31（8）：96－101．

［9］师汉民．影响机床颤振的几个非线性因素及其数学模型［J］．华中工学院学报，1984，12（6）：102－112．

SHIHan-min．Effects of some non-linear factors on machine tool chattering and theirmathematicalmodels［J］．Journal of Huazhong Institute of Technology，1984，12（6）：102－112．

［10］Huang N E，Shen S S P．Hilbert-Huang transform and its applications［M］．Singapore：World Scientific Publishing Co．Pte．Ltd．，2005．

［11］Peng Z K，Tse P W，Chu F L．A comparison study of improved Hilbert-Huang transform and wavelet transform：application to fault diagnosis for rolling bearing［J］．Mechanical Systems and Signal Processing，2005，19：974－988．

［12］Faltermeier R，Zeiler A，Tom A M，et al．Weighted sliding empiricalmode decomposition［J］．Advances in Adaptive Data Analysis，2011，3（4）：509－526．

Cutting chatter recognition based on H ilbert-Huang transform

JIAGuang-fei1，2，WU Bo1，HU You-min1
（1．State Key Laboratory of Digital Manufacturing Equipment＆Technology，Huazhong University of Science and Technology，Wuhan 430074，China；2．School ofMechanical Engineering，HebeiUniversity of Science and Technology，Shijiazhuang 050018，China）

Considering the nonlinear and non-stationary features of cutting chatter signals，a chatter recognition method based on Hilbert-Huang transform was proposed．In themethod，a chatter signalwas decomposed into a series of intrinsic mode functions（IMFs）by empirical mode decomposition（EMD），and then the IMF with rich chatter information was selected and filtered by a band-pass filter，and then the Hilbert spectrum of the filtered IMFwas obtained by Hilbert transform．Finally，the cutting chatter was quantitatively recognized by calculating the amplitude standard deviation of the Hilbert spectrum．The effectiveness of the proposed method was validated by using simulated and actual vibration signals．For comparison，the results by the methods of wavelet packet decomposition and wavelet spectrum analysis were also provided．

Hilbert-Huang transform；cutting chatter；empiricalmode decomposition

TN911．7

：A

10．13465／j．cnki．jvs．2014．22．034

国家重点基础研究发展计划（973计划）（2011CB706803）；国家自然科学基金项目（51175208）；河北省科技支撑计划（13211823）

2013－09－12 修改稿收到日期：2014－01－09

贾广飞男，博士生，副教授，1973年生

吴波男，博士，教授，博士生导师，1963年生