磁流变冲击后坐控制系统试验研究
张莉洁,常家东,王 炅,程广伟
(1.洛阳理工学院机械工程系,河南 洛阳 471023;2.南京理工大学机械工程学院,南京 210094)
磁流变冲击后坐控制系统试验研究
张莉洁1,常家东1,王 炅2,程广伟1
(1.洛阳理工学院机械工程系,河南 洛阳 471023;2.南京理工大学机械工程学院,南京 210094)
针对磁流变阻尼器用于火炮后坐缓冲时对响应时间的严苛要求,对磁流变冲击后坐控制系统进行冲击试验研究。对设计的磁流变阻尼器进行固定电流下冲击特性试验,获得输出阻力模型。对阻尼器线圈电流及输出阻力响应时间分别进行试验测试,提出磁流变冲击后坐轨迹跟踪控制系统方案,期望可控阻力能准确跟踪理想阻力曲线。通过用固定曲线无反馈控制及双闭环反馈控制对磁流变后坐控制系统进行3 g、4 g药量冲击试验结果比较知,采用反馈控制能显著减小磁流变后坐阻力响应时间,获得快速跟踪性能,后坐阻力充满度更好。后坐位移相同时可减小后坐阻力峰值;后坐阻力峰值相同时可显著减小后坐位移。由4g药量中后坐阻力曲线下滑结果分析知,阻尼力可调系数作为重要特性参数在进行磁流变阻尼器结构设计时必须足够大。
磁流变阻尼器;冲击载荷;反后坐装置;响应时间;轨迹跟踪系统
以磁流变液为介质的磁流变阻尼器(Magneto-rheological dampers)因具有结构简单、阻尼力实时可控、能耗低等特点在航空及武器装备缓冲系统中应用前景广阔[1-2]。将磁流变阻尼器用于火炮反后坐装置代替制退机并实时控制,以获得理想后坐动态特性、提高火炮发射的稳定性及射击精度。高冲击载荷下火炮后坐过程非常迅速,仅几百毫秒。在极短时间内实现后坐阻力实时可控对磁流变阻尼器控制系统响应时间提出严苛要求。需对磁流变阻尼器响应时间进行论证。对用于汽车、车削及转子等减振系统的磁流变减振器响应时间均有详细研究及论述[3-6],对磁流变冲击后坐缓冲应用研究大多集中于后坐控制方法论述[7-9]。而普遍忽略评价控制系统优劣的重要指标即动态响应时间,缺乏明确阐述及相关试验论证,磁流变冲击后坐控制系统本质仍有待揭示。
本文针对冲击载荷下磁流变阻尼器响应时间问题,利用阻尼器输出阻力模型对响应时间试验测试及分析。考虑响应时间提出磁流变冲击后坐跟踪控制系统设计方案及双闭环反馈控制算法,以提高系统响应时间及抗干扰能力为目的,期望后坐阻力达到理想的跟踪控制效果;并通过冲击试验验证控制效果及后坐动态特性。
1 磁流变阻尼器冲击动态特性分析
1.1 固定电流冲击试验
冲击试验台架见图1,仅安装磁流变阻尼器,未安装复进装置。磁流变阻尼器为长行程单出杆单筒式,内径50 mm。阻尼器缸筒安装在轴套内与后坐配重质量块固连,活塞杆与地面支座固连。试验通过密爆发生器产生冲击源,阻尼器缸筒受冲击载荷后带动后坐配重质量块沿导轨产生相对活塞杆的后坐运动。缓冲器起保护台架作用,当后坐运动到达缓冲器位置时提供缓冲,避免刚性碰撞。台架最大行程600 mm。测试缸筒后坐时动力参数。

图1 磁流变阻尼器冲击试验台架实物图Fig.1 Impact test facility for MR damper
冲击后坐中磁流变阻尼器作为缓冲器将瞬间产生的极大能量冲击载荷转化为作用时间长、峰值低的后坐阻力作用于机架。后坐过程运动微分方程[10]为
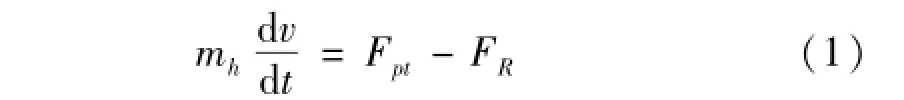
式中:Fpt为冲击载荷;mh为后坐质量;FR为后坐阻力;FR=FMR+FФ+Ff,FMR为磁流变阻尼器阻尼力,由安装在支座与活塞杆上的力传感器测得,FФ为复进机力,未安装时FФ=0,Ff=200 N为后坐接触构件间摩擦力。
由动能定理,后坐行程为λ时,为使后坐阻力FR总功抵消冲击载荷总功,应满足
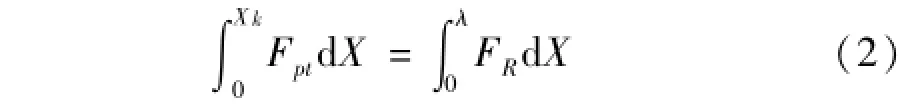
相同后坐位移λ时为使FRmax最小,应使FR=常数。后坐曲线“充满”矩形面积,即应保证良好的充满度,见图2。采用磁流变阻尼器代替传统制退机,以期利用其阻力实时可控性改善后坐动态特性。
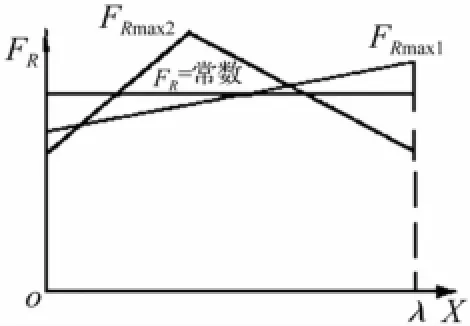
图2 做功面积相同的几种后坐阻力变化规律Fig.2 Variation rules of recoil force at the same power area
用3.2 g火药量分别对磁流变阻尼器线圈施加0 A、0.8 A、1.5 A、2 A固定电流,获得后坐诸元曲线,见图3。由于爆炸冲击力远大于后坐阻力,冲击瞬间后坐阻力可忽略不计。由冲量定理知,冲击冲量大小决定后坐速度峰值。由图3(a)看出,后坐速度峰值可判断各次试验火药量存在差别,各次冲击力不完全相等;且后坐过程结束前速度反向,说明阻尼器在此处微量反弹,此因磁流变阻尼器的滞回特性所致。图3(b)为阻尼力与速度比较,后坐速度达到峰值时后坐阻力峰值同时出现,且阻力峰值随所加电流增大而增大,显示磁流变阻尼器输出阻力的可控性。
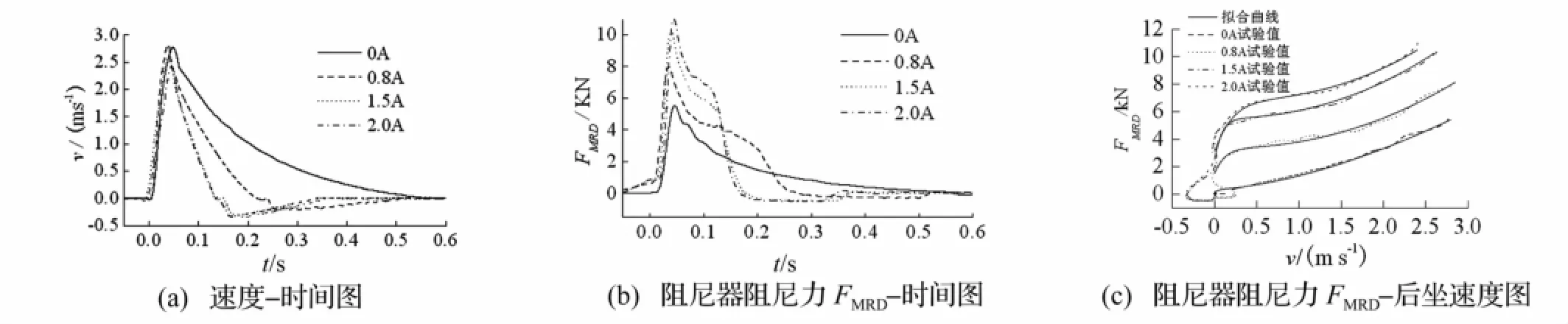
图3 不同电流后坐诸元曲线图Fig.3 Curves of v,FMRD-t,FMRD-v for MR recoil damper at different currents
1.2 建模分析
速度达峰值后因惯性力作用输出阻力与后坐速度vr成指数函数关系[11],见图3(c)。通过曲线拟合及参数辨识可得磁流变阻尼器输出阻力简化模型[11-12],即

式中:vr为后坐速度。该模型将磁流变阻尼力分为两部分,第一部分与后坐速度vr有关,反映流体粘滞阻尼特性,称粘性阻尼力,记Fη;第二部分Fτ与磁流变液屈服强度τy有关,其大小受工作电流控制,称可调库仑阻尼力。Fτ为磁流变阻尼器阻尼力可控部分[12]。
该模型虽与实测曲线有一定误差,但可实现阻尼力随速度、电流变化的完全解耦;遵循复杂问题简单化、去末求本思想,该模型在对磁流变阻尼力实施快速线性控制算法时体现出重要的实用价值。
1.3 后坐控制原理论述
由图3(b)看出,在固定电流下后坐速度峰值过后磁流变输出阻力FMRD随时间逐渐下滑,充满度不好。因此,通过施加适当工作电流增大可调阻尼力Fτ,补偿粘性阻力随后坐速度下降,从而保证充满度饱满。磁流变冲击后坐控制目的在于使可调库伦阻力Fτ按理想曲线输出,属于跟踪控制问题,要求系统快速响应。
2 磁流变阻尼器冲击响应时间测定
2.1 电磁电路响应时间测定
磁流变阻尼器输出阻力响应时间具体指[13]磁流变阻尼器从感知扰动(输入控制信号变化)至产生稳定的阻力所需时间。本文在阶跃输入下对磁流变阻尼器电磁电路及输出阻力响应时间分别进行测试分析。
磁流变阻尼器电流驱动电路采用脉宽调制PWM(Pulse Width Modulation)电流驱动技术,通过PWM信号对磁流变阻尼器励磁线圈中的电流进行控制,继而产生可控阻力。开关管为MOS-FET,原理见图4。
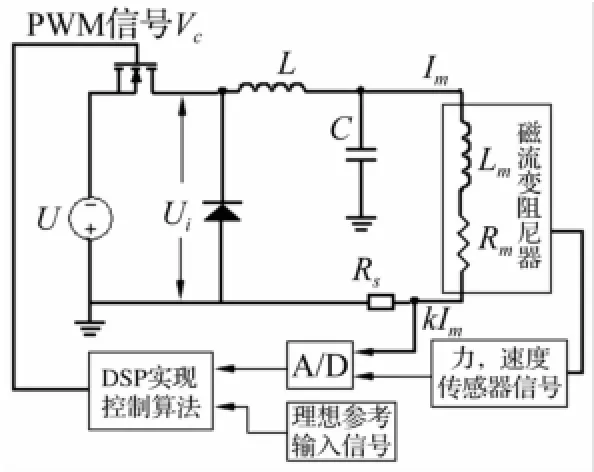
图4 电磁回路原理图Fig.4 The schematic diagram of electromagnetic driver circuit
电路达稳态时阻尼器励磁线圈中电流大小与PWM信号的占空比D成正比例关系,即Im=DU/R。其中U为电源电压。该电路响应时间为毫秒级较短,在对响应时间无苛刻要求的控制系统中可忽略不计,简化为比例环节。但因冲击后坐过程仅几百毫秒,故该电路动态响应时间可能对控制效果产生重要影响,不可忽略[13]。该电路以控制电压Vc(获得一定占空比D的PWM信号)为控制输入,线圈电流Im为输出,电磁电路为三阶系统,其响应时间与磁流变阻尼器负载铁芯线圈电阻及电感大小有关[14],即
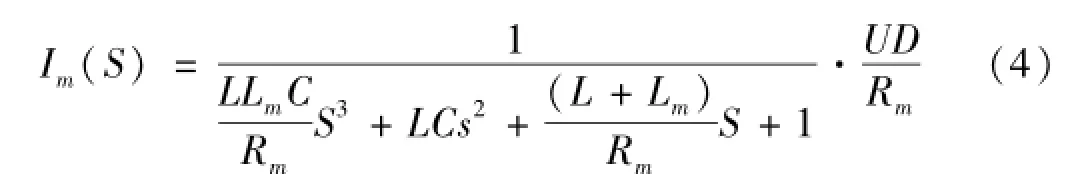
式中:D=5V/Vc为PWM信号的占空比,对电路分别施加阶跃电压控制信号Vc=1.60 V、2.66 V、3.75 V、5.00 V,对应电流Im的稳态值为0.5 A、1 A、1.5 A、2 A。通过电阻Rs对线圈电流进行采样,观察线圈电流信号Im的响应。
为方便信号比较对Vc进行归一化处理,使其值与电流稳态值相等,记为见图5。由于带铁芯线圈的非线性电感作用,对不同输入值Vc系统参数在一定范围内变化,电流响应时间分别为40 ms(0.5 A时),30 ms(1 A时),40 ms(1.5 A时),65 ms(2 A时)不等。且超调量较大。因响应时间较长,难以满足几百毫秒后坐控制要求。因此设计中应考虑对电磁驱动电路进行PI校正,加快电流响应时间。
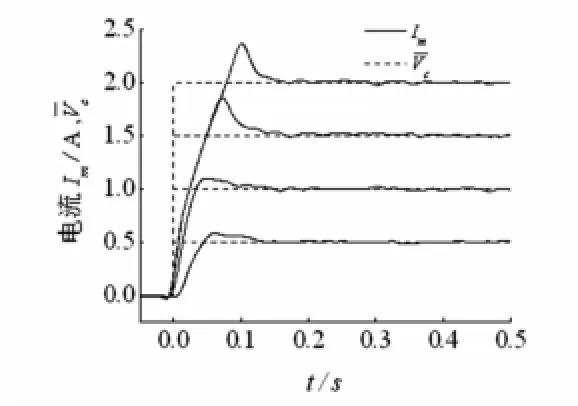
图5 电磁驱动电路电流响应Fig.5 Current response of the electromagnetic driver circuit
2.2 磁流变阻尼器阻尼力响应时间测定
测试阻尼器输出阻力及电流Im对Vc的阶跃响应。火药量4.0 g后坐开始50 ms处对阻尼器施加阶跃电压输入信号Vc分别为1.6 V、2.66 V、3.75 V、5.00 V,对应电流稳态值0.5 A、1 A、1.5 A、2.0 A。Vc=2.66 V,Im=1 A的试验结果见图6。因磁流变输出阻力中仅库伦阻力Fτ受工作电流控制,其粘性力仅与后坐速度vr有关,故本文定义磁流变阻尼器输出阻力响应时间为库仑阻尼力Fτ对工作电流Im的响应时间。由图6(b)中无法观察到阻尼器输出阻力中Fτ的响应时间,此因随后坐速度变化的粘性阻力Fη存在。利用阻尼力模型(式(3))去除随速度变化的粘性阻力,间接获得Fτ,即
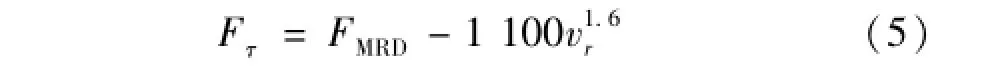
Fτ曲线见图6(c)。为比较Fτ与电流Im的响应时间,将Fτ及Vr归一化处理,使其最大值相同,记为= Fτ/3 300。由图6(c)可观察到Fτ的响应略慢于线圈电流响应,存在短暂延迟,库伦阻尼力相对电流延迟时间(即磁流变液材料响应时间)约8 ms。
由以上分析知,磁流变阻尼器阻尼力响应时间受线圈电磁回路电流响应影响较大,可视为三阶线性系统;而磁流变液材料响应时间可视为延迟单元[13-14]。与电流响应相比,磁流变液材料延迟时间较短且难以调节,因此在磁流变后坐控制系统设计时应对电磁回路进行校正,加快电流响应,提高阻尼器输出阻力响应时间,获得快速跟踪性能。
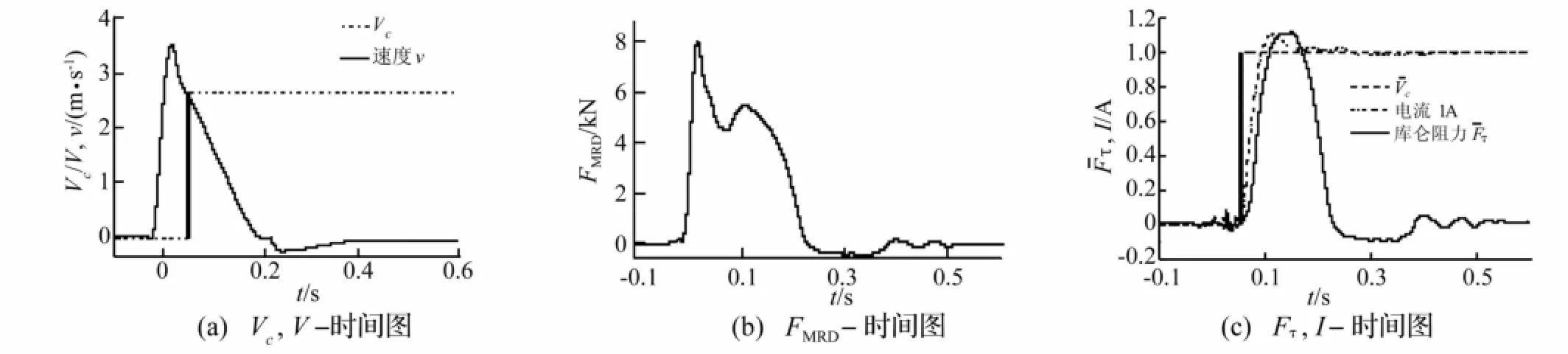
图6 Vc=2.66 V时磁流变阻尼器响应Fig.6 Response time of MR damper at Vc=2.66 V
3 磁流变冲击后坐控制系统研究
3.1 磁流变后坐阻尼控制系统总体方案设计
为获得理想的后坐动态特性,应使后坐阻力FR为常数。由于磁流变阻尼器阻尼力构成中仅Fτ受电流控制,而粘性力Fη由后坐速度vr决定不受电流控制,因此磁流变后坐控制系统为:以线圈电流驱动电路控制电压Vc为控制量,可调库仑阻力Fτ为输出,要求Fτ(t)能快速准确跟踪理想参考库伦阻力曲线Fτr(t),从而获得理想后坐阻力。应离线获得理想库仑阻力曲线Fτr。设理想后坐阻力FRr=常数(图1),由式(1)在matlab下仿真理想后坐过程,获得其速度轨线vrr,再由式(5)得Fτr。
控制区域应在后坐速度峰值后开始(0.03 s处),3.2 g药量下仿真所得Fτr曲线见图7。由图7看出,Fτr逐渐上升以补偿粘性阻力下降。
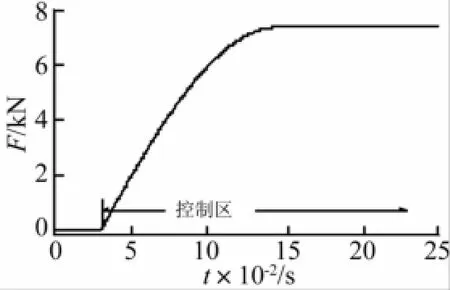
图7 理想库伦阻力Fτr曲线及控制区域Fig.7 Ideal curve of Fτrand determination of the control region
控制系统由控制电压Vc获得库仑阻力Fτ,本身即构成稳定的闭环。为使Fτ能更快速准确跟踪理想曲线,并具有抗干扰能力,本文据闭环反馈思想,拟定双闭环反馈回路对其进行校正,磁流变冲击后坐控制系统方案见图8,具体①内环对阻尼器线圈电磁回路电流进行PI校正,提高电流响应时间;②外环对输出可调库仑阻力Fτ进行误差反馈,消除阻尼力模型误差,提高系统抗干扰性。该控制系统数学模型明确,且控制时间较短,应选快速简洁的PI校正控制。
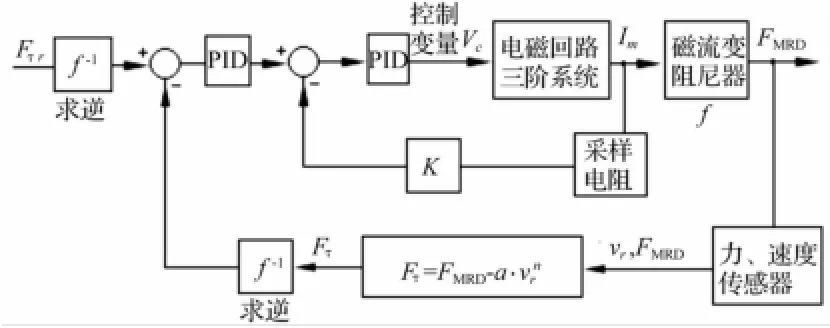
图8 控制系统方案图Fig.8 Scheme of the recoil control system
方案说明:①Fτ反馈计算中考虑实际后坐速度,故该控制系统对后坐过程速度波动及阻力波动均具有抗干扰性。由线圈电流产生的库伦阻力Fτ为非线性环节f,应先用逆系统原理进行反馈线性化,通过取逆Im=f-1(Fτ)消除非线性环节,再利用线性反馈PI控制算法。②电流与库伦阻力非线性关系f-1由动态特性试验测得。为保证运算快速,避免(图8)Fτ指数运算及f-1,在程序中用表格方式实现。
3.2 试验结果
控制系统实现原理见图4。采用dspace硬件在回路系统实现快速原型。试验用3.2 g及4 g两种药量进行测试。对每种药量冲击试验分别采用固定参考曲线Fτr无反馈及双闭环反馈跟踪控制方案。
3.2 g药量试验结果见图9。由图9(b)看出,速度峰值接近,冲击能量相近。后坐时间170 ms时两次后坐位移相近,见图9(a)。由图9(c)、(d)看出,两种控制方法对后坐阻力FR均产生有效控制,而反馈控制曲线更平坦。其速度峰值处两条阻力曲线均出现局部峰值,大小相近。无反馈时速度峰值过后出现明显凹陷(最低点6 417 N),而末端出现凸起峰值(最高点7 501 N),浮动1 084 N;反馈控制曲线相对平坦,阻力峰值出现在速度峰值处,为7 255 N,最小值为7 013 N,仅浮动242 N。后坐位移相同情况下反馈控制较无反馈时阻力峰值减小246 N,后坐特性更理想。其改善原因可由电流Im及Fτ响应时间说明,见图9(e)、(f)、(g)。其中归一化处理后曲线扰动因后坐速度传感器信号波动所致。由图9(e)看出,反馈控制电流响应时间明显加快,能快速跟踪理想电流曲线。比较图9(f)、(g),无反馈及反馈控制下,电流Im到终值2 A的时间分别为114 ms、84 ms,Fτ到终值时间分别为121 ms、89 ms。在38 ms处(对应图9(c)无反馈曲线凹陷处),反馈控制Fτ已达1 677 N,无反馈控制Fτ仅854 N。无反馈控制时(图9(f)),由于Im、Fτ未及时响应,使后坐阻力在38ms处出现凹陷。反馈控制(图9(g))电流Im、Fτ的响应明显加快,使后坐阻力能快速补偿粘性力的下降,未出现明显凹陷。
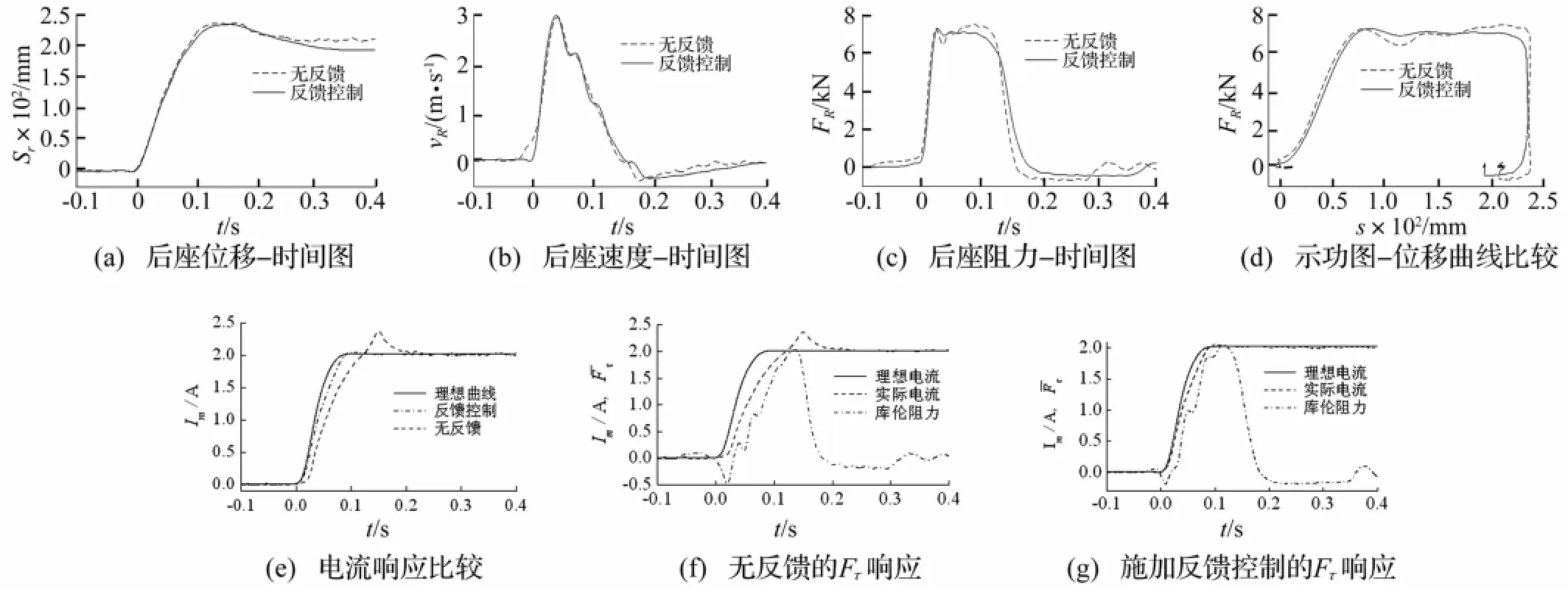
图9 3 g药量后坐控制比较图Fig.9 Curves of MR recoil damper with 3 g powders
4 g药量试验结果见图10。由图10(b)看出速度峰值相等,且图10(d)中两曲线包围面积近似相等,故两次冲击能量相近。比较图10(c)、(d),反馈控制能明显补充无反馈时阻尼力产生的凹陷,充满度更好,显著减小后坐位移(图10(a)),即由300 mm降到270 mm。冲击药量增大后,反馈控制对提高阻尼器响应时间效果更显著,见图10(e)、(f)、(g)。然而亦有不足之处,即两条阻力曲线均为下降趋势(图10(c)),未达理想水平线。其原因为4 g药量冲击载荷增大,后坐速度峰值增大,导致粘性阻力峰值增大,粘性阻力峰值(对应速度峰值处)达9 280 N。而库伦阻力Fτ最大只能达7 300 N,后坐临近结束时速度趋近零,粘性阻力降为零,剩余的库伦阻力7 300 N无法使总阻尼力保持水平。
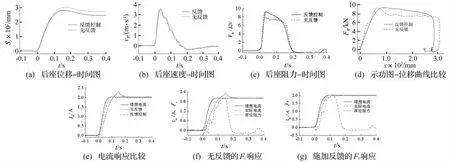
图10 4 g药量后坐控制比较图Fig.10 Curves of MR recoil damperwith 4 g powders
库伦阻力与粘性阻力最大值的比值称为可调系数,决定磁流变阻尼器阻尼力的可控范围。该值由阻尼器结构设计决定。试验结果表明,结构设计中若可调系数达不到,则无论施加何种控制方法也无法获得饱满的后坐阻力充满度。因此,可调系数作为重要几何特性参数在进行磁流变阻尼器结构设计中应足够大。
4 结 论
两种药量的冲击试验充分验证了磁流变冲击后坐控制系统响应时间对后坐动态特性的重要性。试验结果总结如下:
(1)磁流变阻尼器响应时间受电磁电路电流响应影响较大,影响输出阻力的跟踪性能。用理想轨迹跟踪控制方案及PID双闭环反馈控制算法可有效加快后坐阻力动态响应,使充满度饱满,可获得良好的后坐动态特性。
(2)4 g药量试验用反馈控制虽可加快后坐阻力动态响应,但充满度不够。由于磁流变阻尼器可调阻力相对粘性力不足,设计时应保证足够大的可调系数,以增大阻尼力可控范围,以使大药量时亦能获得饱满的充满度。
[1]Ahmadian M,Poynor J C.An evaluationg of magneto rheological dampers for controlling gun recoil dynamics[J].Shock and Vibration,2001,8(3):147-155.
[2]Ahmadian M,Appleton R,James A.An analytical study of fire out of battery using magneto theological dampers[J].Shock and Vibration,2002,9:129-142.
[3]周渊,张永亮,刘军,等.一种剪切式磁流变车削减振器的设计与减振试验[J].振动与冲击,2013,32(4):167-172.
ZHOU Yuan,ZHANG Yong-liang,LIU Jun,et al.Design and test of a sheartype MR damper for turning vibration suppression[J].Journal of Vibration and Shock,2013,32(4):167-172.
[4]祝长生.盘型磁流变流体阻尼器悬臂转子系统响应时间测试[J].航空动力学报,2006,21(3):550-555.
ZHU Chang-sheng.Response time measurement of a cantilever rotor with a disk-type Magnetorheological fluid damper[J].Journal of Aerospace Power,2006,21(3):550-555.
[5]郭鹏飞,关新春,欧进萍.磁流变液阻尼器响应时间的实验研究及其动态磁场有限元分析[J].振动与冲击,2009,28(6):1-5.
GUO Peng-fei,GUAN Xin-chun,OU Jin-ping.Experimental study and dynamic magnetic finite element analysis on the response time of Magnetorheological fluid dampers[J].Journal of Vibration and Shock.,2009,28(6):1-5.
[6]董小闵,丁飞耀,管治,等.面向高速的磁流变缓冲器多目标优化设计及性能研究[J].机械工程学报,2014,5:1-8.
DONG Xiao-min,DING Fei-yao,GUAN Zhi,et al.Multiobjective optimization and performance research of magnetorheological absorber under high speed[J].Chinese Journalof Mechanical Engineering,2014,5:1-8.
[7]李赵春,王炅.基于磁流变阻尼器的冲击缓冲系统控制方法[J].南京理工大学学报,2012,36(4):656-661.
LI Zhao-chun,WANG Jiong.Control methods for shock isolationg system using Magnetotheological fluid damper[J].Journal of Nanjing University of Science and Technology,2012,36(4):656-661.
[8]Hu Hong-sheng,Jiang Xue-zheng,Wang Jiong,et al.Design,modeling,and controlling of a large-scalemagnetorheological shock absorber under high impact load[J].Journal of Intelligent Material Systems and Structures,2012,23(6):635-645.
[9]Li Zhao-chun,Wang Jiong.A gun recoil system employing a magnetorheological fluid damper[J].Smart Materials and Structures,2012,21(10):105003.
[10]高树滋.火炮反后坐装置设计[M].北京:兵器工业出版社,1995:71-79.
[11]张莉洁,王炅.冲击载荷下磁流变阻尼器动态特性分析及模型参数辨识[J].机械工程学报,2009,45(1):211-217.
ZHANG Li-jie,WANG Jiong.Dynamic performance analysis and model parameter identifications of mr dampers under impact load[J].Chinese Journal of Mechnical Engineering,2009,45(1):211-217.
[12]Wang X J,Gordaninejad F.Study of field-controllable,electro-and magneto-rheological fluid dampers in flow mode using herschel-bulkley theory[J].Smart Structures and Materials 2000:Damping and Isolation,Proceeding of SPIE,2000,3989:232-243.
[13]Koo J H,Fernando D.Goncalves.Investigation of the respose time of magnetorheological fluid dampers[J].Damping and Isolation,Proc.of SPIE,2004,5386:63-71.
[14]Yang G,Spencer Jr B F.Large scale MR fluid dampers:modeling and dynamic performance considerations[J].Engineering Structures,2002,24:309-323.
Experiments on magneto-rheological recoil control system
ZHANG Li-jie1,CHANG Jia-dong1,WANG Jiong2,CHENGGuang-wei1
(1.Dept.of Mechanical Engineering,Luoyang Institute of Science and Technology,Luoyang471023,China;2.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)
Since the critical demand for time response of MR damper in gun recoil buffering applications,experimental studies on MR recoil control system were carried out on an impact test rig with the special designed MR damper.The impact performance of the MR damper described by a physical model under fixed operating current was obtained.The time responses of the MR damper's coil current and the damping force were respectively tested,then a trajectory tracking control scheme for MR recoil system was put forward,so that the adjustable damping force of MR can accurately track an ideal reference curve.Experimental results with 3g and 4g powders under the double close-looped feedback control aswell as the fixed damping curve controlwithout feedback were obtained.By comparisons,it is shown that the feedback control can efficiently reduce the response time of the damping force and provide more rapid tracking ability.With the same displacement,smaller peak of recoil force is produced,while with the same peak of recoil force,more less displacement is achieved.Analyzing the decline of the damping force curve with 4g powders,it’s suggested the adjustable coefficient of the damping force,as an important parameter,must be large enough in MR dampers’structural design.
magneto-rheological damper;impact loading;recoil buffering;response time;trajectory tracking control
TH113.1
:A
10.13465/j.cnki.jvs.2014.22.021
国家自然科学基金资助项目(50675106);国家自然科学基金(51175265)
2014-02-14 修改稿收到日期:2014-06-27
张莉洁女,博士,讲师,1976年12月生

