数控机床切削稳定性分析及实验研究

杨毅青，刘 强

（北京航空航天大学机械工程及自动化学院，北京 100191）

数控机床切削稳定性分析及实验研究

杨毅青，刘 强

（北京航空航天大学机械工程及自动化学院，北京 100191）

针对因机床结构的复杂性及零件加工轨迹不确定性，刀尖频响函数切削中难以保持恒定易造成稳定域图变化，导致机床切削参数选择不确定性问题，结合模态实验分别研究数控机床沿不同进给方向及机床主轴处于不同位置的颤振稳定域图预测；对同型号两台数控机床的切削稳定性进行对比分析。由实验采集切削中声音信号验证机床沿不同进给方向的切削稳定性存在差别。研究结果对实际加工中避免切削颤振及工艺参数选择具有指导意义。

铣削；颤振；稳定域图；进给方向

颤振为发生于数控机床铣削加工的强烈自激振动现象。其不仅会降低生产效率，亦能致工件加工表面质量下降、刀具磨损加剧及主轴功率剧增。因此，切削颤振已成制约高速、高效切削的重要因素。

切削颤振稳定域图预测可避免铣削颤振，并已得到广泛应用［1］。Altintas等［2］提出的铣削颤振稳定域图解析预测方法仅需获取刀具与工件材料接触区域的频响函数、切削力系数，实现简单，获得大量引用及推广［3］。用该方法Engin等［4］对各种立铣刀颤振稳定域预测进行研究；Ozsanin等［5］研究实验过程中加速度计重量对刀尖频响函数及稳定域瓣影响；Movahhedy等［6］研究高速铣削中主轴陀螺效应对颤振稳定域瓣影响。Song等［7］基于颤振稳定域及半带宽理论，以材料去除率为目标函数、以稳定切削且非共振为约束条件，提出铣削系统的切削参数与结构参数优化方法。梁睿君等［8］通过有限元仿真获得薄壁零件不同加工阶段模态及各阶段颤振稳定域预测图。李中伟等［9］用Magnus展开式取代原分段常值函数近似方法，提高了零阶半离散法预测铣削系统稳定性的收敛速度。诸多研究均通过沿机床坐标X、Y方向测试获取刀尖频响函数，进而获得不依赖机床位置及走刀轨迹的固定颤振稳定域图。而在实际零件加工中机床位置及刀具进给方向不断改变，由于机床模态方向性及机床结构非对称性，此改变会导致稳定域图预测产生偏差，造成机床切削参数选择的不确定性。基于此，通过用缩减模型子结构综合法，Law等［10］研究虚拟环境下机床位置与机床切削颤振间关系，提出机床优化设计方案。Kersting等［11］通过将薄壁件简化为解耦后的谐振单元，研究随位置变化的零件动力学特性及颤振稳定域预测。

本文以两台同型号三轴立铣床为例，结合模态测试及切削实验，通过预测机床360°范围内颤振稳定域图，分析影响数控机床切削稳定性因素，包括机床进给方向、机床主轴位置等。与常用的仅通过测试机床X、Y方向刀尖频响函数颤振稳定域预测不同，本文研究有助于全面了解机床的切削稳定性，进而提高切削参数选择的准确性。

1 铣削颤振稳定域

再生效应可引发铣削颤振。由于加工工艺系统的柔性Φ在切削力F作用下加工后工件表面残留振纹，导致下一刀齿切削周期实际切削厚度h变化，进而引发切削力F变化，如此周而复始会导致系统发生强烈的自激振动，见图1。

图1 铣削再生颤振效应Fig．1 Regenerative chatter effect ofmilling

再生颤振效应表达式为

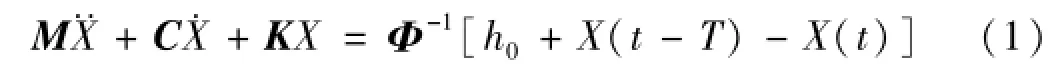
式中：M，C，K分别为系统质量、阻尼、刚度矩阵；T为刀齿切削周期；h0为静态切削厚度；Φ为刀具／工件接触区域的频响函数矩阵，可沿两相互正交方向通过模态测试获取（通常为机床X、Y轴方向，如Φxx与Φyy）；X（t），X（t－T）分别为当前与上一刀齿切削周期时刀具振动位移。

颤振稳定域的临界切深计算式为

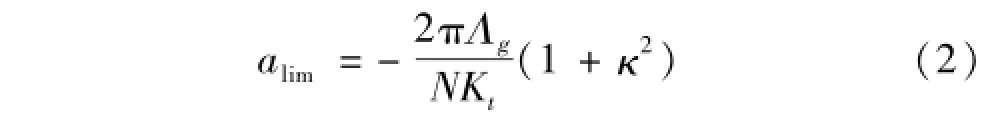
式中：N为刀齿数；Kt为切向切削力系数；Λg，κ为方程求解的过程量［1－2］。

为研究进给方向及主轴位置对机床切削稳定性影响，将测试多方向组合的频响函数矩阵（如30°与120°方向，60°与150°方向等），并结合式（1）、（2）进行稳定域图预测。

2 数控机床铣削颤振稳定域分析

2.1 实验准备

以图1的VMC0850B三轴立铣床为实验对象，研究进给方向、主轴位置对铣削颤振稳定域影响。通过模态实验获取刀尖频响函数，所用力锤、加速度计及数据采集卡型号分别为PCB086C03、Kistler8776A50、NI 9233。模态测试及分析软件为Cutpro V9．3。测试刀具为圆柱螺旋立铣刀（山特维克R216．34），刀齿数N＝4，刀具直径D＝12 mm，螺旋角30°，刀具悬长52 mm。

图2 实验测试机床VMC0850BFig．2 Machine tool VMC0850B for the experiment

2.2 基于进给方向的铣削颤振稳定域图

由机床坐标系X正向（0°）开始，以30°角为间隔，顺时针依次测试刀尖频响函数，共测试12角度。机床加速度频响函数见图3，在2 830 Hz、3 571 Hz、4 535 Hz等频率处有明显模态，不同测试方向的频响函数幅值变化较大。以3571 Hz模态为例，270°方向幅值最小，为791．9m／s2／N；300°方向幅值最大，为1 028 m／s2／N。

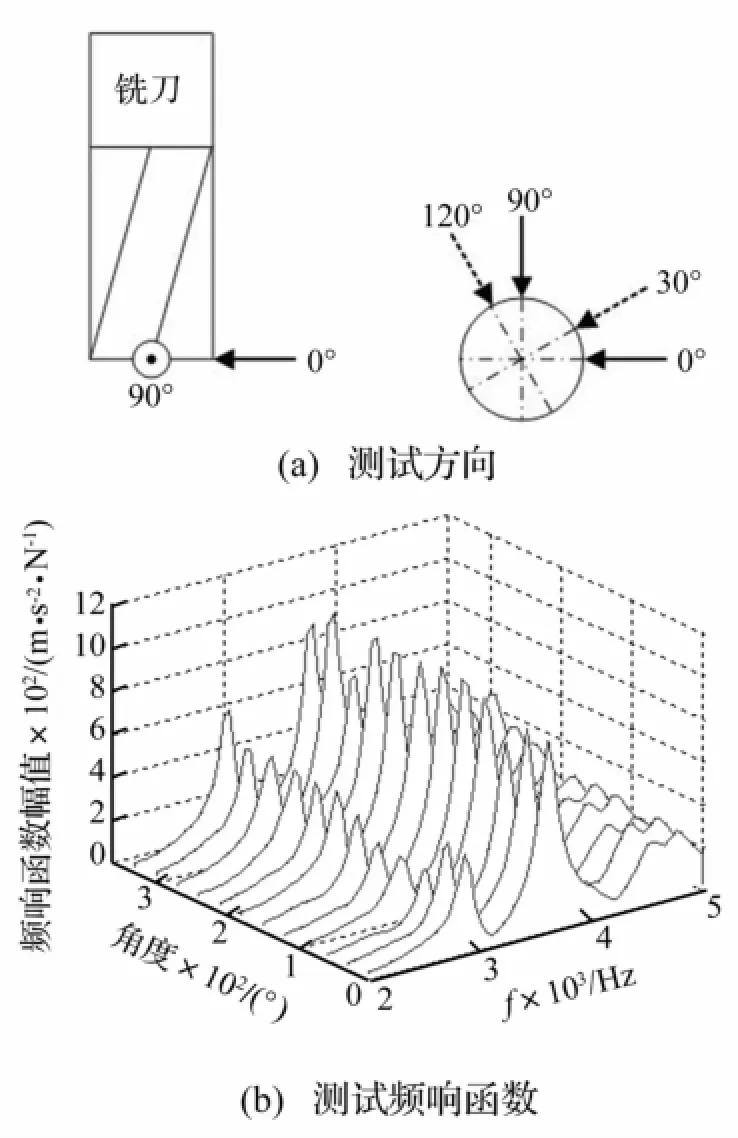
图3 不同进给方向的机床刀尖频响函数Fig．3 Frequency response function of the tool tip under different feed direction

以槽铣铝合金2A12为例，预测主轴位置Z＝－250 mm时沿不同进给方向的颤振稳定域图见图4。图中径向坐标为颤振稳定域最小临界切深，角坐标为进给方向，曲线封闭区域内分别为稳定切削区及不稳定切削区。由图4看出，由于机床结构的非对称性，机床许用稳定切深随进给方向发生变化，最小值为0．92 mm，沿60°方向；最大值为1．02 mm，沿300°方向。

2.3 基于主轴位置的铣削颤振稳定域图

改变机床主轴Z方向位置，分析主轴位置对颤振稳定域图影响。以槽铣加工及主轴处于最低Z＝－250 mm、中间Z＝0 mm、最高Z＝250mm三位置为例，见图5。由图5看出，主轴处于最低位置时许用稳定切深为1．02 mm（300°方向）；主轴处于中间位置时许用稳定切深为1．12 mm（120°方向）；主轴处于最高位置时许用稳定切深为1．60 mm（0°方向）。据机床结构，主轴位置越高悬伸越小，刚性越好，可用稳定切削区域更大。且稳定域图沿300°方向基本对称。

图4 360°角域内机床切削稳定性（Z＝－250 mm）Fig．4 Machine tool chatter stability in the 360°domain（Z＝－250 mm）

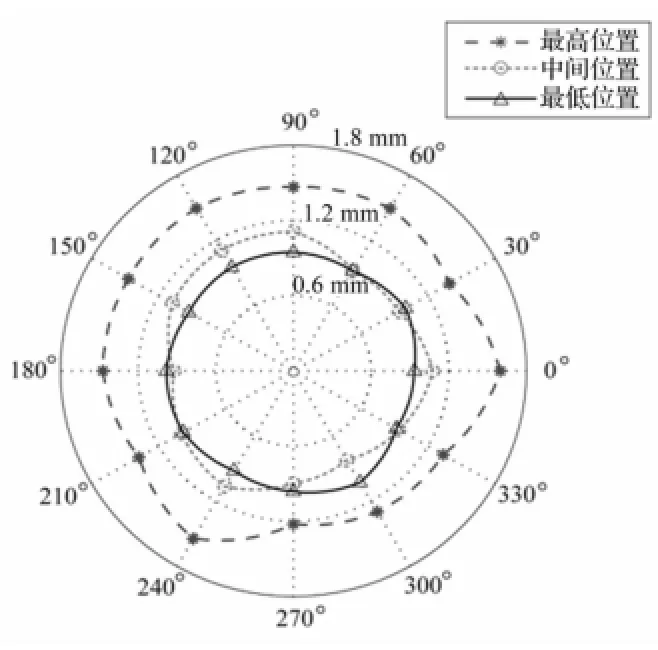
图5 不同主轴位置处机床1切削稳定性（槽铣）Fig．5 Stability ofmachine tool＃1 with different spindle position（slotmilling）

图6 不同主轴位置处的机床2切削稳定性（槽铣）Fig．6 Stability ofmachine tool＃2 with different spindle position（slotm illing）

2.4 同型号数控机床颤振稳定域图对比

选同型号第2台VMC0850B铣床，重复测试及颤振稳定域图预测，并与机床1对比，见图6。由图6看出，机床2对应Z＝－250 mm、0 mm、250 mm的许用稳定切深分别为0．86 mm、0．90 mm、1．64 mm。可见，尽管机床型号相同，但由于设计、装配、使用等原因，两台铣床切削性能存在一定差别。以0°方向频响函数为例，两台机床辨识后第1阶模态参数对比见表1。

表1 两台机床第1阶主模态参数对比（0°方向）Tab.1 Modal parameters com parison for the tw o machine tools of the samemodel

3 切削实验

3.1 实验条件

选机床1进行切削实验。刀具、工件条件与稳定域预测相同。选主轴转速n＝4 000 r／min，进给速度F＝300 mm／min，切宽ae＝12 mm，由圆柱形零件外侧向中心切削。据颤振稳定域图仿真逐渐增加切深，直至发生颤振为止，并改变进给方向重复实验。为比较不同进给方向时的振动情况，用麦克风采集切削中声音信号，见图7。

图7 切削实验及声音信号采集ig．7 Cutting tests and acquisition of sound signals

3.2 实验数据及分析

在D＝12 mm，n＝4 000 r／min，F＝300 mm／min，ae＝12 mm时采集切削中颤振临界状态发生的部分声音信号。图8（a）～（d）分别为沿0°、60°、90°、330°方向进给的时域信号，对应切深分别为1．0 mm、1．0 mm、1．0 mm、1．1 mm。依次对上述信号进行频谱分析，结果见图8（e）～（h）。由图8看出，机床切削时的颤振频率为2 851 Hz，可判断颤振由2 830 Hz模态引发。由于该模态频率较高，结合模态分析结果可认定此模态源于刀具。因刀具结构较对称，反映在频响函数上可发现不同进给方向时该模态对应的幅值均较接近（图3），切削实验表明数控机床在不同进给方向的临界稳定切深差距不大，仅0．1 mm。若忽略刀具模态，仅考虑机床结构模态影响，Z＝－250 mm时所得机床切削稳定性见图9。由图9看出，因机床结构不对称，不同进给方向的许用临界切深差别较大，最大值3．86 mm（240°方向），最小值2．27 mm（30°方向）。

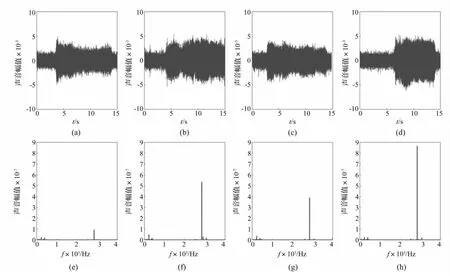
图8 切削中的时、频域声音信号Fig．8 Sound signals of themachining in the time and frequency domain

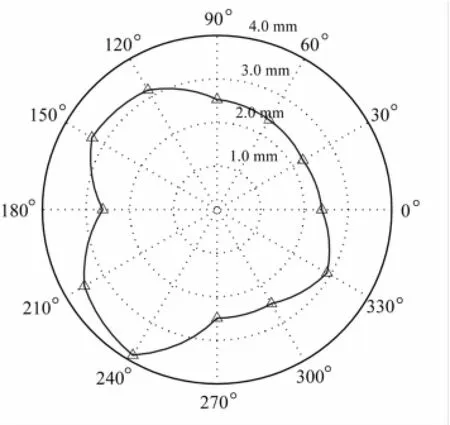
图9 忽略刀具模态的机床切削稳定性Fig．9 Machine tool chatter stability of neglecting the cuttermode

3.3 实验二

将刀具换成肯纳（ABDF2000A2AS K600）再次试切。刀齿数N＝2，刀具直径D＝20 mm，刀具悬长52 mm。选切削参数n＝4 000 r／min，F＝450 mm／min，ap＝5 mm，ae＝20 mm。沿0°及90°进给方向切削的声音信号见图10，图10（a）、（b）为时域信号，（c）、（d）为频域信号，此时切削均处于稳态过程。由于机床沿各方向刚度各异，导致切削过程中振动不一，致声音信号强弱发生变化。

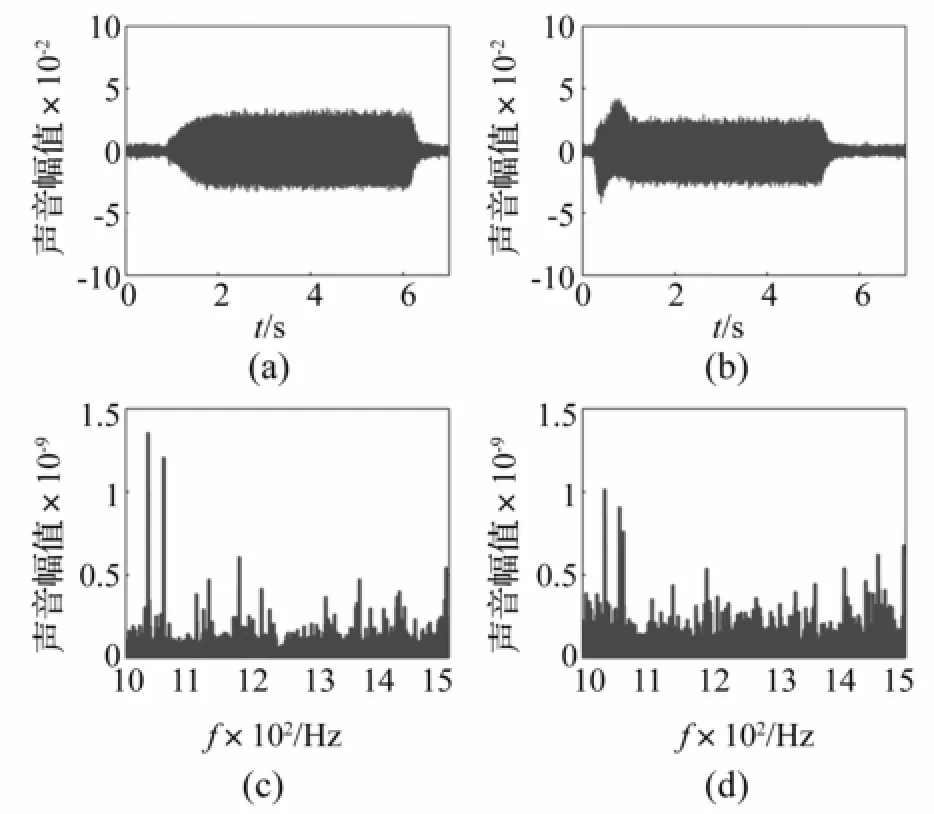
图10 切削过程时频域声音信号Fig．10 Sound signals of themachining in the time and frequency domain

4 结 论

本文以同型号两台立铣床为例，结合测试及切削实验预测机床360°范围内颤振稳定域图，结论如下：

（1）机床结构的非对称性，使进给方向对颤振稳定域有一定影响；许用稳定切深随进给方向发生变化。对两台同型号铣床，不同位置及进给方向的颤振稳定域图预测结果存在一定差别。

（2）通过采集切削过程中声音信号并进行频谱分析，可对切削过程稳定性进行判断。切削颤振由刀具模态引起，且刀具结构相对对称，在不同进给方向的临界稳定切深的差别不大；但若机床存在明显弱刚性模态，不同进给方向的切削稳定性差别会更明显。

［1］刘强，李忠群．数控铣削加工过程仿真与优化－建模、算法与工程应用［M］．北京：航空工业出版社，2011．

［2］Altintas Y，Budak E．Analytical predication of stability lobes in milling［J］．Annals of the CIRP，1995，44（1）：357－362．

［3］Quintana G，Ciurana J．Chatter in machining processes：a review［J］．International Journal of Machine Tools and Manufacture，2011，51（5）：363－376．

［4］Engin S，Altintas Y．Mechanics and dynamics of general milling cutters．part I：helical end mills［J］．International Journal of Machine Tools and Manufacture，2001，41（15）：2195－2212．

［5］Ozsahin O，Ozguven H N，Budak E．Analysis and compensation ofmass loading effect of accelerometers on tool point FRFmeasurements for chatter stability predictions［J］．International Journal of Machine Tools and Manufacture，2010，50（6）：585－589．

［6］Movahhedy MR，Mosaddegh P．Prediction of chatter in high speed milling including gyroscopic effects［J］．International Journal of Machine Tools and Manufacture，2006，46（9）：996－1001．

［7］Song Q H，Wan Y，Ai X，et al．Novelmethod for dynamic optimization of stability in high-speed milling system［J］．Transactions of Nanjing University of Aeronautics＆Astronautics，2009，26（3）：184－191．

［8］梁睿君，叶文华．薄壁零件高速铣削稳定性预测与验证［J］．机械工程学报，2009，45（11）：146－155．

LIANG Rui-jun，YEWen-hua．Stability prediction for highspeed milling of thin walled structures and experimental validation［J］．Journal of Mechanical Engineering，2009，45（11）：146－155．

［9］李中伟，龙新华，孟光．基于Magnus-Gaussian截断的铣削系统稳定性的半离散分析法［J］．振动与冲击，2009，28（5）：69－73．

LI Zhong-wei，LONG Xin-hua，MENG Guang．Stability analysis of milling process by semi-discretization method based on Magnus-Guassian truncation［J］．Journal of Vibration and Shock，2009，28（5）：69－73．

［10］Law M，Altintas Y，Phani A S．Rapid evaluation and optimization ofmachine toolswith position-dependent stability［J］．International Journal of Machine Tools＆Manufacture，2013，68：81－90．

［11］Kersting P，Biermann D．Modeling workpiece dynamics using sets of decoupled oscillator models［J］．Machining Science and Technology：An International Journal，2012，16（4）：564－579．

Analysis and experimental investigation on the cutting process stability ofmachine tool

YANG Yi-qing，LIU Qiang
（School of Mechanical Engineering and Automation，Beihang University，Beijing 100191，China）

Machining chatter is an important factor of restricting high speed cutting，and chatter stability prediction is an effectivemethod to avoid chatter by using themeasurement of the tool tip frequency response functions（FRF）in the X／Y directions of themachine tool coordinate system．Owing to the complexity ofmachine structure and uncertainty of tool path，the tool tip FRFs are varied during the cutting process which therefore causes the variation of stability charts and influences the cutting parameters selection．The stability charts with different feed directions and spindle positions were investigated based on the modal test，and the machining performance of two machine tools of the same model were compared．Cutting tests were carried out，and the machining stability performance along different feed directions was analysed according to the sound signals collected duringmachining．The results are beneficial to the chatter reduction and cutting parameters selection in the realmanufacturing process．

milling；chatter；stability chart；feed direction

TG506；TG547

：A

10．13465／j．cnki．jvs．2014．22．018

国家自然科学基金（51205013）；教育部博士点基金（20111102120048）；中央高校基本科研业务费（YWF－12－LZGF－179）

2013－08－01 修改稿收到日期：2013－11－15

杨毅青男，博士，讲师，1983年生