激振底座与叠层芯片悬臂相互作用研究
李进军,韩 雷
(中南大学机电工程学院,长沙 410083)
激振底座与叠层芯片悬臂相互作用研究
李进军,韩 雷
(中南大学机电工程学院,长沙 410083)
利用动态频率扫描对叠层芯片进行激振,用双探头激光多普勒测振仪同时测量底座激振下悬臂叠层芯片底座及悬臂端速度,对比分析二者响应速度频谱获得两悬臂与底座相位差;分析悬臂共振时对底座影响及两悬臂相互作用关系,准确获得芯片悬臂端共振频率。该实验方案合理可行,对微结构动力学分析及精确数值仿真具有一定指导意义。
叠层悬臂结构;双探头激光测振;共振频率;频率响应曲线;相位差;动态频率扫描
微结构动态特性测试中底座激振为常用激励方法。该方法无需在构件上附加或制备元件,且对微构件材料、制作工艺等无特殊要求,为常用激励方法[1-6]。由于激励时处于振动状态的微结构与底座构成复杂系统,故激振底座会对待测件的输出信号产生一定影响。文献[7]以压电陶瓷为激振底座,用多普勒激光测振仪测得微型悬臂叠层芯片两悬臂端共振频率;但因未考虑悬臂与底座间相互作用及共振峰检测的灵敏度不够,易造成误识别。
本文采用双探头多普勒激光测振仪[8]同时测量叠层芯片悬臂端及底座,获得悬臂、底座在动态扫频激励下的速度频谱曲线及悬臂端、底座相位差曲线,并分析两悬臂及芯片底座的相互作用,可较准确地获得两悬臂共振频率。
1 激振与测试
待测结构为由两块尺寸为矩形硅芯片垂直堆叠而成的“+”型悬臂叠层芯片,上层芯片两端呈悬臂状,上下层芯片间由环氧树脂胶粘接固化,见图1。悬臂端共振频率与结构尺寸、材料特性有关。悬臂实际长度应为悬臂端至环氧树脂胶粘合处长度,但较难精确控制胶液量及胶液形状,无法保证两悬臂完全对称,故叠层芯片两悬臂端共振频率不同。预估计叠层芯片两悬臂共振频率约在100~300 kHz之间。
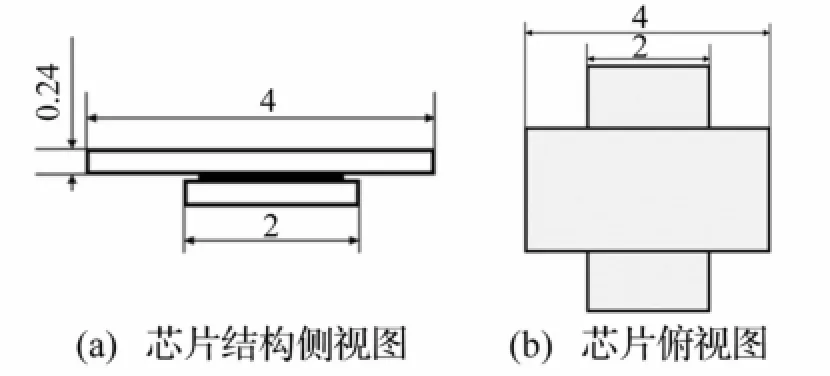
图1 叠层芯片结构示意图(单位:mm)Fig.1 Stacked chip
采用丹麦Noliac公司的NAC2025型压电陶瓷(PZT),尺寸5 mm×5 mm×2 mm,参数见表1。

表1 NAC2025压电陶瓷主要参数Tab.1 Parameters of NAC2025 PZT
将芯片底座用502胶粘贴于压电陶瓷厚度方向,见图2(a)。底座指芯片上层芯片中间与下层芯片粘合部分,悬臂指上层芯片两端悬空部分。待测系统能量传递方式见图2(b),压电陶瓷推动芯片底座振动,芯片底座推动两悬臂产生振动。实验测试点为(图2(a))中两悬臂测点与中心测点,简称悬臂1、悬臂2、底座。
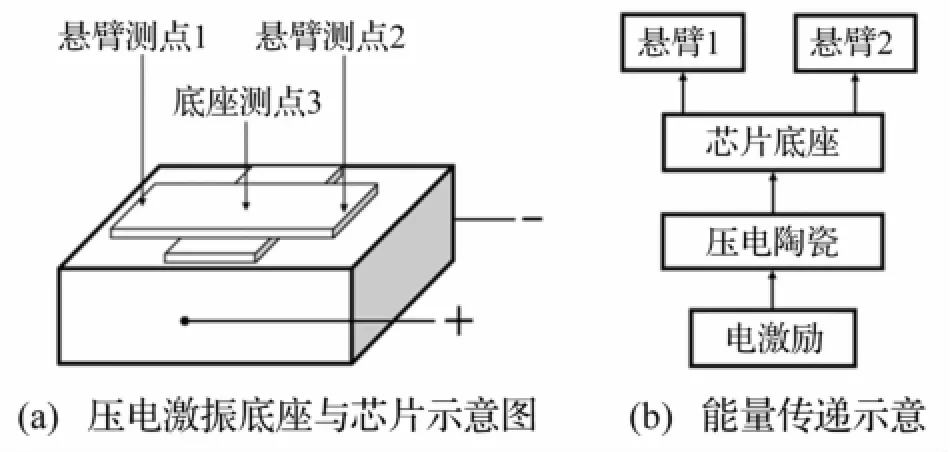
图2 悬臂叠层芯及压电陶瓷Fig.2 Stacked chip and piezoelectric ceramics
实验系统见图3,压电陶瓷在Agilent 33120A任意波形信号发生器驱动下产生振动对叠层芯片进行激励,用扫描式激光探头PSV-400-M2(探头1)及单点式激光探头OFV-505/5000(探头2)分别测量芯片悬臂端、底座振动速度。探头1距待测芯片约1 m,探头2距待测芯片约1.3 m。两激光探头可同时采集芯片底座、芯片悬臂端振动信号。
2 实验结果与讨论
共振峰检测可采用稳态频率扫描的激励方法[9],但稳态激励耗时且因激振点、测试点离散,易丢失品质因数较高的峰值。而采用动态频率扫描激励[10]及双探头则能较快检测到两悬臂共振频率,并以较高分辨率表征悬臂、底座的相互作用。将探头1、探头2分别对准悬臂测点1及底座测点4中间(图2(a)),设置Agilent33120A信号发生器输出电压为5 V、扫描周期(sweep period)10 ms、扫描范围100~300 kHz的循环电激励信号(图3)激励压电陶瓷。
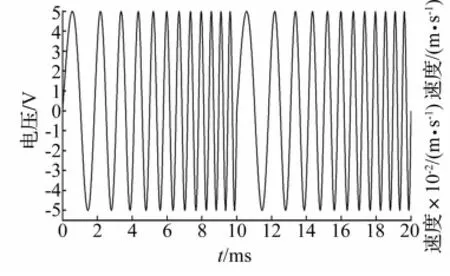
图4 循环扫频电激励信号Fig.4 Cyclic sweep electric excitation signal
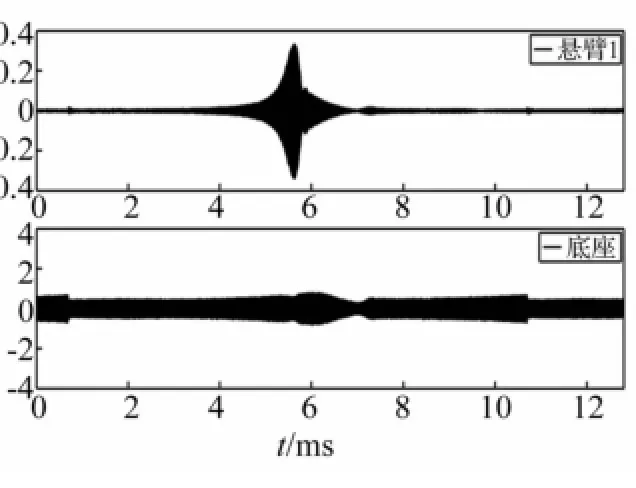
图5 同时采样所得悬臂1及底座速度Fig.5 Sample data
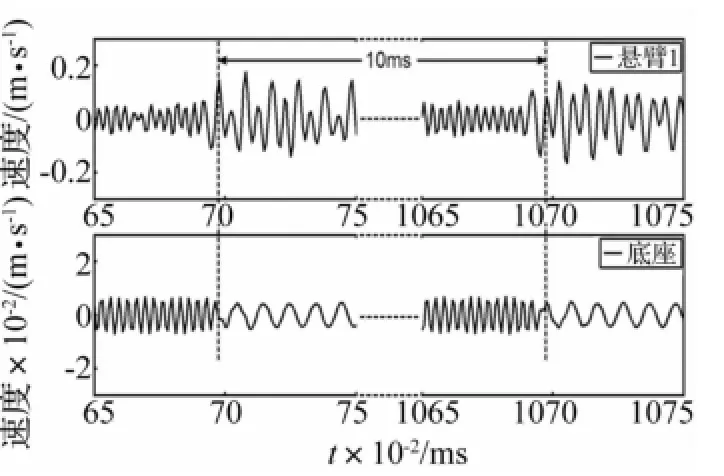
图6 一个扫频周期两端速度曲线Fig.6 Sweep cycle ends
多普勒测振仪采样时间12.8 ms,两激光探头同时采集悬臂端、芯片底座响应速度V1(T)、V1b(T),见图5。预估悬臂、底座振幅分别在0.3μm与10 nm以内。两激光探头同时采集12.8 ms内悬臂1、底座振动速度,扫频周期仅10 ms,扫频周期两端多出2.8 ms上个扫频周期末端数据与下个扫频周期前端数据,见图6。截去V1(T)、V1b(T)两端多余数据,获得一个扫描周期(10 ms)内悬臂1及底座响应速度V1(T)、V1b(T),见图7。
保持探头2位置不变,将探头1对准悬臂2端点中间(图2(a))重复测试,获得动态扫频激励下悬臂2与底座的响应速度V1(t)、V1b(t)。对悬臂1及底座速度采样数据V1(f)、V1b(f)进行快速傅里叶变换(FFT),得悬臂1及底座的速度频谱曲线V2(f)、V2b(f)见图8。同理可得悬臂2与底座的速度频谱曲线V2(f)、V2b(f)见图9。实验得芯片B的悬臂及底座速度频谱曲线见图10、图11。
由图8~图11看出,芯片的悬臂共振时底座速度响应幅值有所下降,另一悬臂速度响应幅值在该处亦有所下降。原因为悬臂振动来源于底座的推动,待测系统能量输入不变,一个悬臂共振时能量增加,底座能量则会相应减少,另一悬臂能量也会相应减少,两悬臂会通过底座影响对方而产生影响。当两悬臂共振频率相差较大(图8、图9)、两悬臂共振时对对方影响较小,两悬臂速度频谱曲线峰值明显,判断两悬臂共振频率分别为196.2 kHz及228.6 kHz。而两悬臂共振频率相差较小时,其间相互影响较明显(图10、图11),导致两悬臂速度频谱曲线出现多个峰值,图10中悬臂1两峰值分别为210.7 kHz,219.9 kHz,图11中悬臂2两峰值分别为210.7 kHz,220.9 kHz,较难判断峰值是否对应真实共振频率。故由原始频谱数据获得悬臂、底座速度幅值比,剔除底座振动对悬臂速度幅值影响。该幅值比峰值对应的方为悬臂真实共振频率。
悬臂1频率响应函数为H1(f)=V1(f)、V1b(f),悬臂2无量纲频率响应函数为H2(f)=V2(f)/V2b(f)。获得芯片A、B两悬臂频率响应曲线见图12、图13。由图12可准确判断芯片A两悬臂共振频率分别为196.2 kHz,226.6 kHz,此共振频率应较图8、图9中共振频率更准确。两悬臂通过底座相互作用使两条频率响应曲线在对方共振峰处均出现一小峰值。由图13看出,芯片B两悬臂共振频率相差较小,相互影响较明显,悬臂1频率响应曲线峰值为217.2 kHz,悬臂2频率响应曲线有两个峰值215.1 kHz,217.2 kHz。悬臂2峰值频率217.2 kHz受悬臂1共振影响所致,215.1 kHz应为悬臂2的共振频率。故芯片B的两悬臂共振频率分别为217.2 kHz,215.1 kHz。悬臂1的共振使悬臂2频率响应曲线多出一个峰,而悬臂2共振却未使悬臂1的频率响应曲线产生附加峰。此因为两悬臂通过底座间接影响对方,底座与压电陶瓷粘接,质量较悬臂质量大得多,悬臂对底座影响较微弱,两悬臂间相互影响也亦较微弱。仅当悬臂共振速度幅值较另一悬臂速度幅值大得多时才会对另一悬臂产生明显影响。
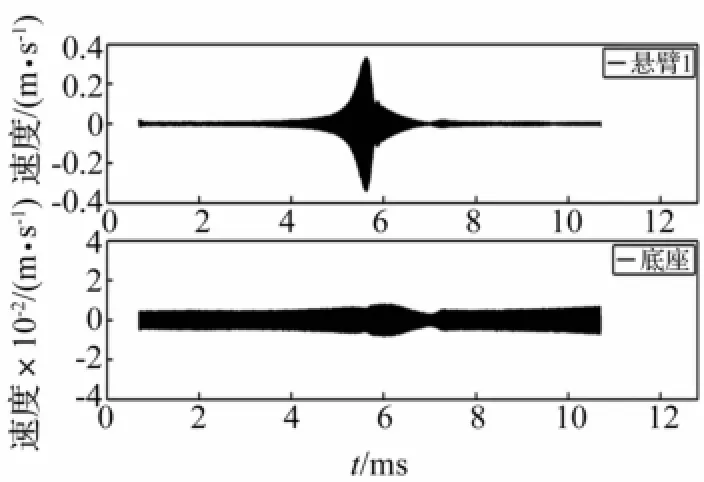
图7 处理后悬臂1及底座速度Fig.7 Processed data
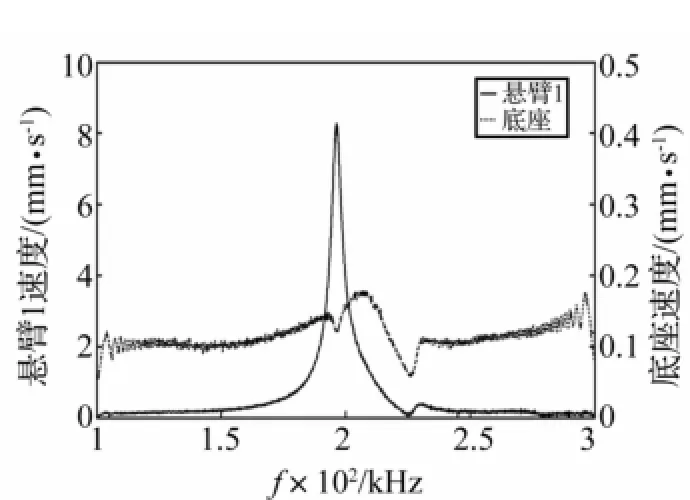
图8 芯片A悬臂1及底座速度频谱曲线Fig.8 Chip A,velocity spectrum curve
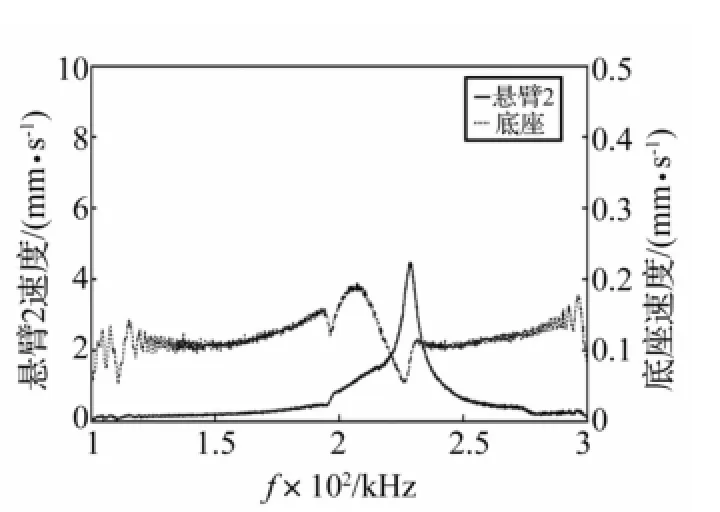
图9 芯片A悬臂2及底座速度频谱曲线Fig.9 Chip A,velocity spectrum curve
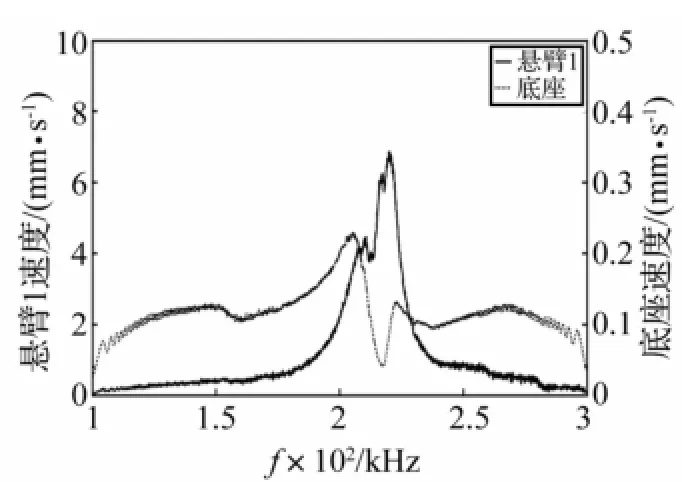
图10 芯片B悬臂1及底座速度频谱曲线Fig.10 Chip B,velocity spectrum curve
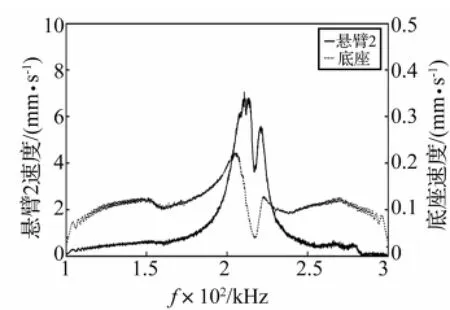
图11 芯片B悬臂2及底座速度频谱曲线Fig.11 Chip B,velocity spectrum curve
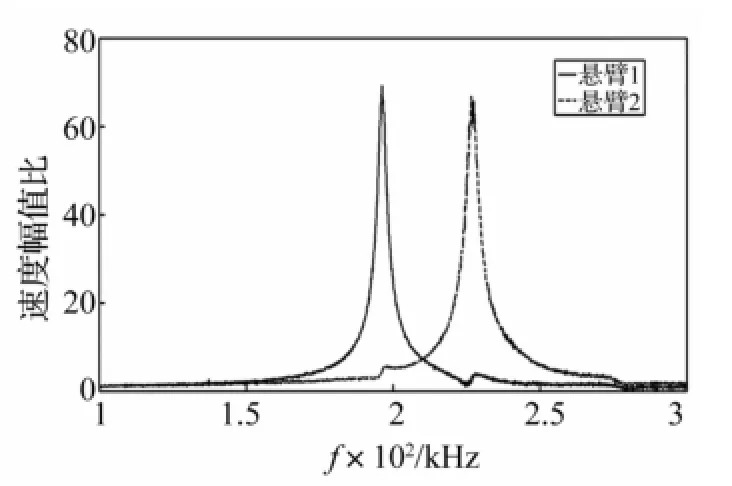
图12 芯片A两悬臂频率响应曲线Fig.12 Chip A,frequency response curve
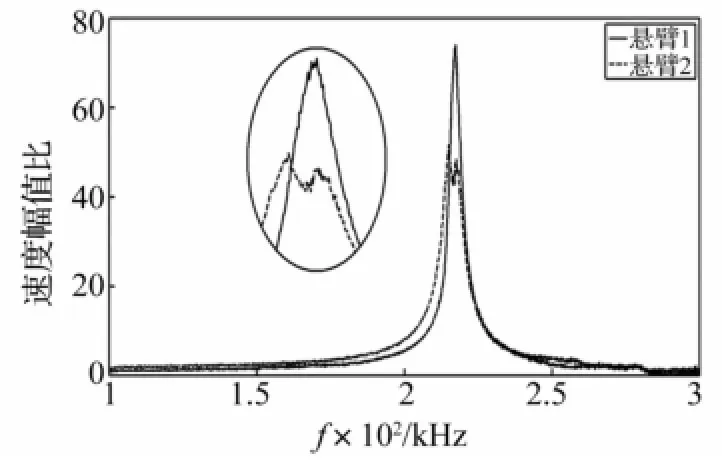
图13 芯片B两悬臂频率响应曲线Fig.13 Chip B,frequency response curve
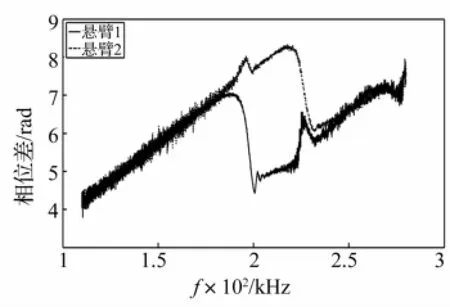
图14 芯片A动态激励下两悬臂与底座相位差Fig.14 Chip A,phase between cantilever and base
用希尔伯特变换[11-12]求得动态扫频激励下芯片A两悬臂及底座间相位差曲线见图14。由图14看出,悬臂1共振时与底座相位差急剧减小,受悬臂1共振影响,悬臂2与底座相位差曲线出现一个峰值;悬臂2共振时亦然。在非共振区域内两悬臂与底座相位差基本一致。
观察底座与悬臂振动动力学模式图像,若同时获得其振动数据,则受迫振动的底座与悬臂应有确定的振动相位差。该相位差与悬臂材料特性、尺寸、测点位置及激振频率有关,随频率的增高而增加。当激振频率逼近悬臂共振频率时,两悬臂相位差应发生(幅值不超过π)跳变,出现悬臂间“反相”同步振动。由实验图像已证实测试与数据分析方法可信,可用于深入讨论微结构动力学行为。
3 结 论
通过对所检测悬臂端振动信号的底座激励实验方法进行改进,用两激光探头同时获取底座、悬臂端振动信号并对比分析,结论如下:
(1)悬臂共振时底座响应速度幅值会相应降低,因系统能量输入稳定,悬臂共振时动、势能大大增加,底座动、势能会相应减少,影响另一悬臂响应速度幅值,两悬臂通过底座间接影响对方。
(2)两悬臂共振频率十分接近时相互影响更明显,两悬臂速度频谱曲线更复杂,较难判断悬臂速度频谱曲线与共振频率关系。故应取悬臂与底座的响应速度幅值比即悬臂频率响应曲线,该曲线峰值对应的方为悬臂共振峰。
(3)底座质量、刚度较大,故悬臂对底座影响较弱。两悬臂通过底座使对方产生的间接影响亦较微弱;仅当一个悬臂共振响应速度幅值较另一悬臂在该频率下响应速度幅值大较多时才会明显影响另一悬臂。
(4)悬臂1共振时与底座相位差会急剧减小,悬臂2与底座相位差会略有增加,悬臂2共振时亦然。在非共振频率范围内两悬臂与底座相位差几乎相同。
[1]Epp D S,Ozdoganlar O B,Chaplya P M,et a1.A base excitation test facility for dynamic testing of m icrosystem[C].Proc.21st International Modal Analysis Conf.Dearborn Detroit USA,2004:26-29.
[2]LaiW P,Fang W.Determining the in-plane and out-of-plane dynamic response ofmicrostruetures using pulsed dual-mode ultrasonic array transducers[J].Sensors and Actuator A,2005,117:186-193.
[3]Lai W P,Fang W.Novel bulk acoustic wave hammer to determinate the dynamic response of microstructures using pulsed broad bandwidth ultrasonic transducers[J].Sensors and Actuator A,2002,96:43-52.
[4]Lai W P,Fang W.Improvement of bulk acoustic wave hammer for vibration testing of microstructures using 1~3 composite transducers[J].Sensors and Actuator A,2002,101:99-106.
[5]Chou Y F,Wang LC.On themodal testingofmicrostructures:its theoretical approach and experimental setup[J].Journal of Vibration and Acoustics,2001,123:104-109.
[6]王晓东,杨洋,佘东升,等.MEMS微构件动态特性测试的激励技术和方法[J].测试技术学报,2008,22(5):377-386.
WANG Xiao-dong,YANG Yang,SHE Dong-sheng,et al.Excitation techniques for testing of dynamic characteristics of MEMSmicrostructure[J].Journal of Test and Measurement Technology,2008,22(5):377-386.
[7]韩雷,严国政.底座激振下微型叠层芯片共振频率检测[J].振动与冲击,2012,31(7):153-157.
HAN Lei,YAN Guo-zheng.Resonant frequency measurement for amicro stacked chip with base excitation[J].Journal of Vibration and Shock,2012,31(7):153-157.
[8]Siringoringo D M,Fujino Y.Experimental study of laser doppler vibrometer and ambient vibration for vibration-based damage detection[J].Engineering Structures,2006(28):1803-1815.
[9]Liu C H,Barzilai A M,Reynolds JK,et al.Characterization of a high-sensitivity micromachined tunneling accelerometer withmicrog resolution[J].Journal of Microelectromechanical Systems,1998,7(2):235-244.
[10]蔡晨光,樊尚春.基于Polytec激光测振仪的微振动测试分析系统[J].测控技术,2004,23(4):5-7.
CAIChen-guang,FAN Shang-chun.Test and analysis system ofmicro vibration based on Ploytec laser doppler vibrometer[J].Measurement&Control Technology,2004,23(4):5-7.
[11]周增建,王海,郑胜峰,等.一种基于希尔伯特变换的相位差测量方法[J].电子质量,2009(9):18-20.
ZHOU Zeng-jian,WANG Hai,ZHENG Sheng-feng,et al.Measuringmethod for phase difference based on hilbert transform[J].Electronics Quality,2009(9):18-20.
[12]胡广书.数字信号处理理论、算法与实现(第二版)[M].北京:清华大学出版社,2003:363-405.
Interaction between exciting base and cantilever of stacked chip
LIJin-jun,HAN Lei
(College of Mechanical&Electrical Engineering,Central South University,Changsha 410083,China)
A two-probe Laser Doppler Vibrometer(LDV)system was used for detecting the vibrations of the cantilever and the base.The velocity spectra of the cantilever and base were comparatively analysed,and then the dimensionless frequency response of the cantilever,and the phase difference between the cantilever and base were acquired,based on which the resonant frequency of the cantilever was estimated accarately.The effect of the cantilever resonance on the base vibration and the interaction between the two cantileverswere analysed.
stacked cantilever structure;two-probe laser vibrometer system;resonant frequency;frequency response curve;phase curve;dynamic frequency scanning
TB52+3
:A
10.13465/j.cnki.jvs.2014.22.017
国家重点基础研究发展计划(2009CB724203)
2013-07-24 修改稿收到日期:2013-11-08
李进军男,研究生,1986年生
韩雷男,教授,博士生导师,1955年生邮箱:leihanxyz@163.com

