广义特征值问题的快速傅里叶变换法
吴 锋,徐小明,钟万勰
(大连理工大学工业装备结构分析国家重点实验室,工程力学系,辽宁大连 116024)
广义特征值问题的快速傅里叶变换法
吴 锋,徐小明,钟万勰
(大连理工大学工业装备结构分析国家重点实验室,工程力学系,辽宁大连 116024)
针对广义特征值问题提出离散傅里叶变换法。该方法把结构的动力响应看作是一种信号,利用快速傅里叶变换进行分析,从而得到结构的振动频率。该方法避免对刚度矩阵求逆,可同时计算出所有的特征值,是一种直接方法。数值算例验证了该方法的正确性。
特征值;动态结构响应;快速傅里叶变换;采样
在工程中,结构振动频率分析和稳定分析都涉及到广义特征值问题。关于广义特征值问题已经提出许多算法[1-9],其中常用的算法有子空间迭代法、Ritz向量法、Lanczos算法等[4,6]。这些方法均为迭代方法,通常是利用一组基,把大规模的广义特征值问题转化成一个小规模的特征值问题,然后再用直接解法求解这一小规模特征值问题。对于小规模的特征值问题,通常采用Jacobi算法[2]。一般说来,迭代方法必须结合直接算法才可以进行,而且需要对刚度矩阵求逆,往往只能求解部分特征值。
对于一个结构,其结构振动响应中包含着关于结构振动频率的所有信息,如果把结构的动力响应看作是一组信号,则可以利用信号处理中的快速傅里叶变换进行分析[10,11],从而找到结构的振动频率。在实际结构的模态分析中,常通过对测量得到的结构振动响应进行傅里叶变换,分析其结构的振动频率[12]。实际上,这一思想也可用于计算广义特征值问题。对于一组给定的刚度矩阵和质量矩阵,可以人为构造一种工况,采用计算机仿真计算其动力响应,然后利用快速傅里叶变换进行分析,从而得到特征值。关于结构的动力响应计算有许多成熟算法[13-16]。基于这一认识,本文针对广义特征值问题提出基于结构动力响应的离散傅里叶变换法。该方法把结构的动力响应看作是一种信号,而结构的动力响应可以利用成熟的算法如中心差分法、精细积分法等求解,也可以实际测量,从而避免对刚度矩阵求逆。得到结构动力响应后,利用快速傅里叶变换进行分析。本文方法可以同时计算出所有的特征值,是一种直接方法,也可以与迭代方法结合求解,处理迭代法中需要解决的小规模特征值问题。
1 基本思想
本文考虑结构的广义特征值问题
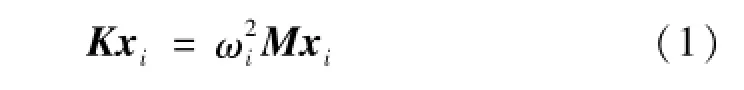
式中:K,M为结构刚度、质量矩阵;x为特征向量;ωi为振动频率。且有
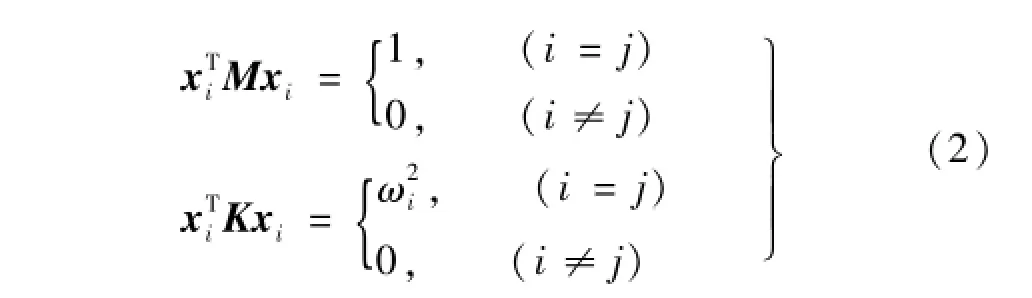
求解式(1)的广义特征值问题常用方法为子空间迭代、Lanczos迭代等。本文提出与此完全不同之方法,即由结构振动响应出发,对结构振动响应进行傅里叶变换,获得结构振动频率。
1.1 自由振动
设某工况下结构振动响应只含结构振动频率,不含其它任何杂质,即无阻尼系统的自由振动。设结构位移向量a,其动力微分方程为

由式(9)可见结构位移响应中只含结构振动频率,对结构位移响应进行傅里叶变换便可获得结构的振动频率。
1.2 时间步长及采样长度
以上分析均基于连续情况,实际计算结构动力响应时只能得到各时间点位移值,故可用快速离散傅里叶变换(FFT)。计算结构动力响应应选精度较好的动力算法。对规模较大动力问题需避免求逆。获得结构在各时间点位移值后须用FFT进行分析,其中时间步长取决于位移中所含最大频率ωmax,而采样长度则取决于位移中两相邻频率之差Δω。设需分析信号为


根据式(15)知,如果频率w为整数时,am=δmw。因此根据am是否等于1,就可以找到频率w。但是因为m≤0.5N,如果w>0.5N,则w≠m,此时对于所有的m有am=0,无法识别出信号的频率,而其截断N项的傅里叶级数为0,傅里叶信号失真。因此仅当w≤0.5N时才可以识别出信号的频率,而其离散傅里叶变换在各个时间点上的值才不会失真。把w≤0.5N代入式(14)可得:

am是关于w的一个复函数,其模为:

因此,|am(w)|是一个关于w和m的函数,当固定w时,m越接近w,|am|越大,而远离m时,|am|只有N-1的量级。现在假设一个信号有两个频率组成,一个为ω,另一个为ω+Δω,该信号离散傅里叶变换后的各个频率的振幅即为:
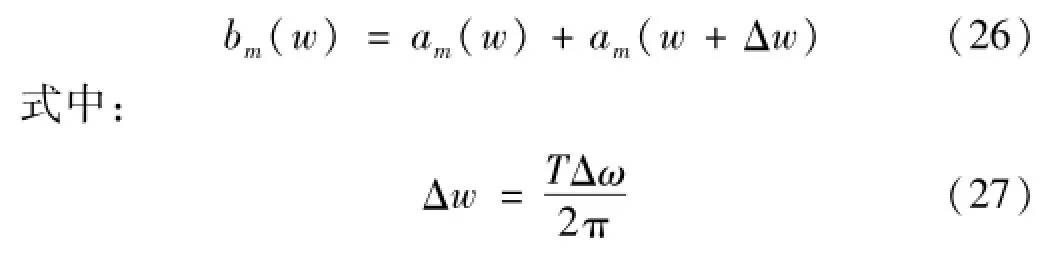
只要函数|bm(w)|出现两个峰值,一个在w处,一个在w+Δw处即可以识别出这两个峰值。当Δw很小时,由于w与w+Δw相处太近,导致两个峰值合成一个峰值,识别不出这两个频率。这是频率分辨率的问题,解决的方法是增加采样长度N,使得在[w]([w]表示距离w最近的整数)和[w+Δw]之间出现明显的波谷,从而把两个峰值明显的隔开。现在假设和[w+Δw]的平均数的整数,要求为一种识别指标),因为


进一步,上式也可以写成ΔωΔt≥8h/N,这一不等式就是测不准原理。当采样点数N固定后,ΔωΔt大于一定值,因此,时域的分辨率Δt越小,则频域的分辨率Δω就大,反之亦然,要想两者都小,则必须增加采样点数。
1.3 最大频率
确定时间步长时需要用到结构的最大振动频率,这一最大振动频率可以根据结构的最小单元的最大特征值确定。当结构的质量矩阵是集中质量阵时,这里基于广义盖尔圆定理[17],给出一个确定最大频率的方法。在标准特征值问题中有个盖尔圆定理,那么对于如式(1)所示的广义特征值问题,我们可以很容易的建立一个广义盖尔圆定理,现在设:
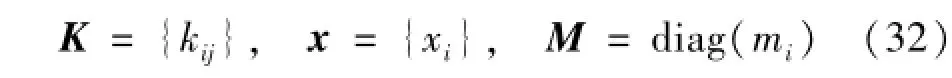
刚度矩阵K中第i行第j列的元素为kij,质量矩阵M为对角矩阵,第i个对角元素为mi,x中第i个元素为xi,则矩阵形式的特征方程可以展开成如下所示的N个方程:

2 算法设计
根据式(38)和式(31)确定时间步长Δt和采样长度N。然后根据式(3)和式(4)计算结构的响应,把响应进行离散傅里叶变换,既可以找到结构的各阶振动频率。在式(38)中,h是一种识别指标,描述了两个相邻频率w和w+Δw的分辨率。当h取得大时,|bm(w)|在这两个频率之间会出现一个明显的波谷,从而可以识别出这两个频率。但是h取值很大时,采样长度就会变大。经过计算发现,取h=5较为合理。当通过傅里叶变换找到各个峰值时,此峰值所对应的频率w为无量纲频率,还需要通过式(14)化成圆频率,也就是结构的振动频率。下面讲述具体计算过程。
(1)根据式(38)和式(31)确定时间步长和采样长度N;
(2)选定初始位移M-1a0,根据式(3)计算结构的自由振动响应;
(3)计算出结构的动力响应之后,任意提取某节点的位移响应作为信号,对该信号进行快速傅里叶变换,得到频域信号;
(4)对频域信号取绝对值,找出频域信号峰值所在的无量纲频率w;
(5)根据式(14),把w化成圆频率,即得到结构的振动频率。
3 算例
计算图1所示20层平面钢框架结构的振动频率。已知框架柱为450×450×25 mm箱型截面,弹性模量E=2.06× 105MPa。按刚性楼板假设,采用层剪切模型,集中质量,每层的质量m=168 750 kg。分别采用传统求解特征值问题的QR法、Jacobi方法和本文方法计算。QR法和Jacobi方法属于迭代法,把QR法相对误差取10-13时的解作为标准解。本文方法计算时,初始位移中a0的各项元素均取为1,识别指标取h=5,计算所用的时间步长按式(38)选取,而频率分辨率取为Δω=0.5。结构的位移响应分别采用精细积分法[11]、中心差分法和文献[12]中所提出的的高精度摄动法计算。经过计算发现,把任一层的位移响应作为时域信号进行快速傅里叶变换,计算结果完全一样,这是因为其时域信号中所包含的频率分量完全相同,这里只给出采用第一层位移响应作为时域信号分析的结果。所有的计算结果列于表1。
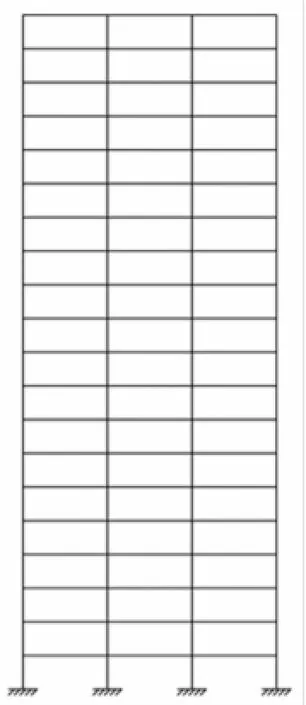
图1 平面框架Fig.1 Plane frame

表1 计算的频率及相对误差Tab.1 Com puted frequencies and relative errors
由表1可见,不管采用哪种方法计算结构的自由振动响应,计算得到的频率完全一样,这说明当时间步长和采用长度选定后,结构的自由振动响应计算手段对计算结果的影响不大。与标准解相比,各阶频率的误差均很小。误差最大的为第1个频率,也只有0.42%,这表明本文方法的可靠性。为进一步比较本文方法和经典的QR法和Jacobi方法的性能,分别取QR法和Jacobi方法的迭代相对误差为0.4%,比较计算时间,结果列于表2。表2中,本文方法计算结构动力响应时采用的是精细积分方法。根据表2可见,对于小规模的广义特征值问题,当相对误差均为0.4%时,本文方法仅需要很少的计算时间即可以给出十分满意的结果。这说明本文方法比较适用于小规模广义特征值问题的求解。根据表1的计算结果还可见,本文方法计算的高阶频率的相对误差要小于低阶频率的相对误差,这一特点不同于传统的迭代方法,在传统迭代方法中,往往高阶频率的相对误差大于低阶频率的相对误差。

表2 计算时间Tab.1 Computation times
4 结 论
本文针对广义特征值问题提出基于结构动力响应的离散傅里叶变换法。该方法把结构的动力响应看作是一种信号,利用快速傅里叶变换进行分析,从而得到结构的振动频率。在本文方法中,结构的动力响应可以利用成熟的算法如中心差分法、精细积分法等求解,也可以实际测量,从而避免对刚度矩阵求逆。本文方法可以同时计算出所有的特征值,是一种直接方法,也可以与迭代方法结合求解,处理迭代法中需要解决的小规模特征值问题。必须指出的是,本文方法是把工程中模态分析的做法进行数值化,从而用于计算广义特征值问题。对于一个复杂的真实结构,其动力响应计算往往要比动力特性计算费时,从这一点上讲,本文方法比较适用于小规模广义特征值问题。但是从两点上讲本文方法仍然是有价值的。
(1)传统的特征值计算方法如QR法、Jacobi方法、子空间迭代法等均为迭代方法,其收敛的理论依据均为反幂法,而本文方法则是基于傅里叶变换理论,因此本文方法是对现有的广义特征值问题的数值算法的一种补充,从数值算法角度上讲,本文方法是有价值的。
(2)本文算法把广义特征值问题看成是结构动力响应问题和信号分析问题来处理,具有鲜明的工程背景。数值算例表明,对于小规模的广义特征值问题,本文方法仅需要很少的计算时间即可以给出十分满意的结果。在本文方法的求解过程中,结构动力响应的计算手段对特征值的计算影响不大。
[1]薛长峰,周树荃.非对称广义特征值问题的并行连续同伦算法[J].计算物理,1997,14(4/5):619-621.
XUE Chang-feng,ZHOU Shu-quan.Parallel homotopy continuation algorithm for nonsymmetric generalized eigenvalue problem[J].Chinese Journal of Computational Physics,1997,14(4/5):619-621.
[2]王顺绪,戴华.广义特征值问题的并行块Jacobi-Davidson方法及应用[J].计算力学学报,2008,25(4):428-433.
WANG Shun-xu,DAI Hua.Parallel block Jacobi-Davidson method for solving large generalized eigenvalue problems and it's application[J].Chinese Journal of Computational Mechanics,2008,25(4):428-433.
[3]刘寒冰,龚国庆,刘建设.一种有效的广义特征值分析方法[J].固体力学学报,2003,24(4):419-428.
LIU Han-bing,GONG Guo-qing,LIU Jian-she.An effective algorithm for generalized eigenvalue problems[J].ACTA Mechanica Solida Sinica,2003,24(4):419-428.
[4]李秀梅,吴锋.广义特征值问题求解的改进Ritz向量法[J].振动与冲击,2012,31(7):19-23.
LI Xiu-mei,WU Feng.Improved Ritz vector method for generalized eigenvalue problems[J].Journal of Vibration and Shock,2012,31(7):19-23.
[5]李海滨,黄洪钟,赵明扬.有限元结构动力分析的广义特征值的神经计算[J].哈尔滨工业大学学报,2006,38(9):1523-1527.
LI Hai-bin,HUANG Hong-zhong,ZHAO Ming-yang.Finite element approach for structural dynamic analysis using generalized eigenvalue-based neurocomputing[J].Journal of Harbin Iistitute of Technology,2006,38(9):1523-1527.
[6]黄吉锋.求解广义特征值问题的多重Ritz向量法[J].力学学报,1999,31(5):585-595.
HUANG Ji-feng.The multi-ritz-vector method in generalized eigenvalue problems[J].Chinese Journal of Theoretical and Applied Mechanics,1999,31(5):585-595.
[7]黄华娟,周永权,韦杏琼,等.求解矩阵特征值的混合人工鱼群算法[J].计算机工程与应用,2010,46(6):56-59.
HUANG Hua-juan,ZHOU Yong-quan,WEIXing-qiong,et al.Hybrid artificial fish school algorithm for solving matrix eigenvalues[J].Computer Engineering and Applications,2010,46(6):56-59.
[8]Nandy S,Sharma R,Bhattacharyya SP.Solving symmetric eigenvalue problem via genetic algorithms:serial versus parallel implementation[J].Applied Soft Computing,2011,11(5):3946-3961.
[9]Li H,Yang Y.The adaptive finite elementmethod based on multi-scale discretizations for eigenvalue problems[J].Computers&Mathematics with Applications,2013,65(7):1086-1102.
[10]刘进明,应怀樵.FFT谱连续细化分析的富里叶变换法[J].振动工程学报,1995,8(2):162-166.
LIU Jin-ming,YING Huai-qiao.Zoom FFT spectrum by Fourier transform[J].Journal of Vibration Engineering,1995,8(2):162-166.
[11]易立强,邝继顺.一种基于FFT的实时谐波分析算法[J].电力系统及其自动化学报,2007,19(2):98-102.
YILi-qiang,KUANG Ji-shun.FFT-based algorithm for realtime harmonic analysis[J].Proceedings of The CSU-EPSA,2007,19(2):98-102.
[12]Schwarz B,Richardson M.Experimentalmodal analysis[J].CSIReliability Week,1999,36(6):30-32.
[13]周杰梁,郑百林.基于中心差分法的纤维结构碰撞动力学分析[J].力学季刊,2011,32(3):466-472.
ZHOU Jie-liang,ZHENG Bai-lin.Impact dynamics analysisof fiber-composed structure based on central difference method[J].Chinese Quarterly of Mechanics,2011,32(3):466-472.
[14]钟万勰.子域精细积分及偏微分方程数值解[J].计算结构力学及其应用,1995,12(3):253-260.
ZHONG Wan-xie.Subdomain precise integration method and numerical solution of partial differential equations[J].Computational Structural Mechanics and Applications,1995,12(3):253-260.[15]李秀梅,吴锋,张克实.结构动力微分方程的一种高精度摄动解[J].工程力学,2013,30(5):8-12.
LI Xiu-mei,WU Feng,ZHANG Ke-shi.A high-precision perturbation solution for structural dynam ic differential equations[J].Engineering Mechanics,2013,30(5):8-12.
[16]李秀梅,吴锋,黄哲华.结构动力方程一种新的级数形式的解析解[J].振动与冲击,2010,29(6):219-222.
LIXiu-mei,WU Feng,HUANG Zhe-hua.New series form of analytical solution for the structural dynamic equations[J].Journal of Vibration and Shock,2010,29(6):219-222.
[17]李秀梅,吴锋,黄哲华.PCG法的理论解释及在结构分析中的应用[J].广西大学学报(自然科学版),2009(4):463-468.
LI Xiu-mei,WU Feng,HUANG Zhe-hua.Theoretical explanation for PCG method and its application in structural analysis[J].Journal of Guangxi University(Natural Science Edition),2009(4):463-468.
Fast Fourier transform method for generalized eigenvalue problems
WU Feng,XU Xiao-ming,ZHONGWan-xie
(State Key Laboratory of Structural Analysis of Industrial Equipment,Department of Engineering Mechanics,Dalian University of Technology,Dalian 116024,China)
For generalized eigenvalue problems,a method based on the fast Fourier transform(FFT)was developed.In the proposed method,the dynamical structural response was viewed as a signal containing all information about the vibrational frequencies.Using FFT to the signal,the vibrational frequencies can be obtained.The method is a kind of direct solution method which can compute all eigenvalues without the matrix inversion.A numerical example manifests the correctness of the proposed method.
eigenvalue;dynamical structural response;fast Fourier transform;sampling
O327;O214.6
:A
10.13465/j.cnki.jvs.2014.22.012
国家基础研究发展计划973(2009CB918501)
2013-08-26 修改稿收到日期:2013-11-15
吴锋男,博士生,1985年生

