加速度计信号奇异值分解滤波与参数辨识

李强 陈雪冬 徐伟

(西南科技大学信息工程学院1,四川 绵阳 621010;中国工程物理研究院电子工程研究所2,四川 绵阳 621900)

加速度计信号奇异值分解滤波与参数辨识

李强1陈雪冬2徐伟1

(西南科技大学信息工程学院1,四川 绵阳 621010;中国工程物理研究院电子工程研究所2,四川 绵阳 621900)

针对石英挠性加速度计模型参数辨识的噪声影响问题,采用奇异值分解技术实现测量信号的滤波降噪处理,再结合总体最小二乘算法实现模型参数的高质量辨识。以重力场下的多齿分度台为测试分析平台,利用样本熵和统计参数定量评价辨识效果。试验结果表明,奇异值分解技术能有效去除信号中的噪声干扰,且通过降噪信号获得的模型系数稳定性较好。所采用方法有效地实现了加速度计参数辨识分析,可用于其性能质量评价。

石英挠性加速度计 参数辨识 奇异值分解 总体最小二乘法 样本熵

0 引言

针对石英挠性加速度计,通过误差补偿可提高其使用精度[1],且跟踪误差模型系数可获取其稳定性描述信息[2],从而避免制造材料及工艺等的限制问题。重力场测试是一项重要基础测试,安装方式上,通过测量角的排列组合标定可解决安装角误差问题[3];辨识方法上,最小二乘与总体最小二乘[4]、神经网络[5]、微粒群优化支持向量机[6]等多种方法得以应用。此外,通过融合遗传算法[7]、半参数回归模型方法[8],提高辨识精度,并通过优化数字滤波[9]及Kalman滤波[10]实现在线误差分析。

在现有研究基础上,本文利用奇异值分解滤波降噪方法提高信号质量,再使用总体最小二乘方法估计加速度计模型系数,进而利用样本熵和统计参数来定量评价加速度计性能。

1 原理与方法

1.1 奇异值分解降噪

石英挠性加速度计在测量过程中,其输出信号不可避免地会引入噪声干扰。这些噪声主要由两类因素造成,一是加速度计的机械结构及其装配工艺所造成的固有机械噪声,二是测量系统中的电子器件因素所引起的电子噪声[11]。因此,为提高后续测试工作的准确性,需要进行降噪预处理。现有的降噪方法中,数字滤波技术较为简单,但是需要获取信号和噪声频带分布的先验信息;小波滤波技术存在小波母函数的选择性问题和分解层数的设置问题;Kalman滤波技术也存在先验统计参数的确定问题。考虑到重力场下的加速度计分度台测试是静态测试过程,每个安装位置下只能获取一种状态特征,且采集到的加速度信号及其噪声信号可认为呈现加性叠加特性。那么,利用奇异值分解(singular value decomposition,SVD)技术便可有效地分离出观测信号中的噪声特征值空间。进而去除这些噪声特征信息,就可通过矩阵重构方式获取降噪后的加速度信号。

由于SVD技术针对的对象是矩阵形式,故需要对采集到的单通道含噪加速度信号x(n)(n=1,…,N)进行矩阵构造。利用基于采样延迟的相空间重构技术,选取原始数据中的前k个采样值(x1,x2,…,xk)为一个子序列,并以此作为相空间矩阵的第一行向量;再移动一个采样步长,将子序列(x2,x3,…,xk+1)作为第二行向量;以此类推,从而获得相空间矩阵的第m行向量,即(xm,xm+1,…,xN)。所构造的相空间形式即为Hankel矩阵。该矩阵为m×k维,满足m≤k且N=m+k-1。

结合单通道含噪信号的加性叠加描述,对其构造Hankel矩阵Hx后,加速度信号能量集中在其特征子空间Hs中,噪声信号能量集中在其特征子空间Hε中。这两个特征子空间的分布有所不同,且呈现出加性叠加过程。结合SVD,有:

式中:Ux和Vx为采集含噪信号的奇异向量矩阵;Us和Vs为加速度信号的奇异向量矩阵;Uε和Vε为噪声信号的奇异向量矩阵;Σx、Σs和Σε为采集信号、加速度信号和噪声信号的奇异值对角矩阵。

从式(1)可以看出,对采集信号的Hankel矩阵进行SVD处理后,保留有效的奇异值并将与噪声相关的奇异值设置为零,则信号中的噪声能量能够得以抑制。那么,利用处理后的奇异值矩阵进行逆向重构,就可获取降噪后的加速度信号[12]。

1.2 总体最小二乘法

在前述降噪处理的基础上,加速度信号质量得以改善,进而实现加速度计模型系数估计精度的提高。石英挠性加速度计在重力场下的完整静态模型可描述为:

式中:E为加速度计输出信号;ai、ap和ao分别为沿输入轴、摆轴和输出轴的加速度分量;K0为偏值系数;K1、K2和K3分别为标度系数、二阶和三阶非线性系数;Kip和Kio分别为输入轴与摆轴、输入轴和输出轴之间的交叉耦合系数;Kp和Ko为相应的失准角系数[1]。

一般地,经典的最小二乘方法常用于加速度计静态模型的参数辨识,但是该方法只考虑了观测信号的测量误差,并假定系数矩阵是无误差的。由于加速度输出信号是利用夹具将加速度计固定在分度台上获得的,此测量过程必然会形成安装误差,所获得的角度观测系数矩阵也将存在误差。因此,引入总体最小二乘(total least square,TLS)方法,其待求问题可描述为:

式中:Ee和Ae为观测数据和系数矩阵的误差项;K为待辨识参数矩阵。

利用式(3)设计增广矩阵,并进行奇异值分解处理,有:

则利用增广矩阵的右奇异向量可获取总体最小二乘的解,从而得到加速度计静态模型系数,即为:

式中:r为待辨识参数的个数。

整体上说,TLS方法充分考虑了采集信号的测量误差问题和由加速度计安装角度引起的测量系数矩阵误差问题,较经典最小二乘方法更符合实际[13-14]。

1.3 样本熵

连续测试过程所辨识出的模型系数将形成相应的时间序列。通过对系数时间序列的分析可实现对加速度计性能的稳定性分析。考虑到时间序列的熵值是随着复杂度变化而变化的,因此,在应用统计均值和标准差的基础上,进一步采用样本熵SaEn来定量描述系数序列的复杂度情况[15-16]。熵值越大,则说明序列变化越复杂;熵值越小,则说明序列变化越规则。

作为传统近似熵的改进算法,样本熵因不包含数据自身的比较运算而不受数据长度的影响,且其结果具有更好的一致性。

针对时间序列y(i)(i=1,…,N),首先构造一组多维矢量,计算两两矢量间的距离,并找出其中的最大距离值,即:

式中:m为所构造矩阵的维数。

设置一个容忍阈值r,针对第i个向量序列统计矢量间距离小于该阈值的数量ni,并结合距离总数将其表示成相对概率形式,再计算所有数据点的相对概率平均值:

进而增加维数至(m+1),重复前面的过程,即可获得此时间序列的样本熵:

2 试验与分析

2.1 试验设置

利用夹具将石英挠性加速度计安装在多齿分度台上,将安装位置均匀分成12点,即安装角度分别设置为0°、30°、60°、90°、120°、150°、180°、210°、240°、270°、300°和330°。利用数据采集卡NI PCI-6221测量不同角度位置下的加速度计输出信号,并将采样率设置为1 000 Hz。

加速度计在分度台上的安装状态可分为两种。在输入轴平行于分度台台面的条件下,当摆轴平行于分度台台面且输出轴平行于分度台转轴时为摆状态,即水平摆安装状态;当输出轴平行于分度台台面且摆轴平行于分度台转轴时为门状态,即侧摆安装状态。那么,在这两种安装状态下,重力加速度将在不同的轴方向上相应形成不同的加速度分量,并用ai、ap和ao表示重力加速度在输入轴、摆轴和输出轴方向上的加速度度分量。结合安装角度θ,摆状态下有:

门状态下有:

将以上两式分别代入模型表达式(2),采用总体最小二乘法便可辨识出相应的模型系数,进而利用统计参数和样本熵来评价其系数稳定性。另外,考虑到重力场环境对加速度计高次项的激励不足等因素[1],侧重选择辨识两种安装状态下的偏值系数与标度系数,并评价其系数稳定性情况。

2.2 试验分析

针对各个安装角度,选取5 s数据用于连续测试分析。利用奇异值分解技术对加速度信号进行降噪处理,其中,Hankel矩阵维数设置为30,且由于每个角度位置表征的是一种状态信息,故仅需保留最大的奇异值,便可重构出降噪信号。然后在系数辨识过程中,通过分析降噪前后的系数变化情况来探讨系数辨识的稳定性问题。

以摆状态为例,在270°安装角度位置下采集的加速度信号如图1(a)所示,采用奇异值分解的降噪信号如图1(b)所示。从图1可以看出,采集信号含有大量的噪声干扰,通过奇异值分解降噪处理后的信号噪声得到抑制,降噪信号能够有效描述加速度计在重力场下的变化过程。

针对摆状态,利用降噪前后加速度信号辨识出来的偏值系数和标度系数变化曲线如图2和图3所示。针对门状态,利用降噪前后加速度信号辨识出来的偏值系数和标度系数变化曲线如图4和图5所示。从图4和图5可以看出,与采集信号和降噪信号的变化趋势类似,采用直接测量信号辨识出的系数变化较大且较为复杂,采用SVD降噪信号辨识出的系数变化较小且较为稳定。进一步地,利用统计参数和样本熵定量评价各个模型系数的连续辨识性能,其中,统计参数包括辨识系数的均值和标准差,样本熵分析维数设置为2,容忍阈值设置为0.2SD (SD表示信号标准差)。获得的摆状态和门状态下统计结果如表1和表2所示。从试验结果来看,加速度信号降噪前后的两个辨识系数的统计均值几乎保持一致,而降噪后的系数统计标准差明显变小;同样,降噪后系数的样本熵要低于采集信号的样本熵。测试试验结果表明,SVD方法取得了满意的降噪效果,且利用降噪信号获得的模型辨识系数克服了采集噪声的影响,其稳定性得以明显提高。

图1 加速度信号降噪处理曲线Fig.1 Noise reduction curves of acceleration signal

图2 摆状态下K0系数曲线Fig.2 K0curves of horizontal pendulum state

图3 摆状态下K1系数曲线Fig.3 K1curves of horizontal pendulum state

综合来看,所研究的石英挠性加速度计性能测试方法以多齿分度台为测试平台,通过连续数据采集方式获取一时间段内的加速度计输出信号,利用样本熵和统计参数来定量分析加速度计的重力场模型参数。其中,所采用的奇异值分解降噪方法能够提高采集信号的质量,所采用的总体最小二乘辨识算法考虑了信号测量误差和加速度计安装角度误差问题,能够提高模型参数的辨识效果。

统计试验说明,所采用测试方法能够有效描述加速度计模型参数的连续变化情况,可用于评价加速度计性能质量。

综合来看,所研究的石英挠性加速度计性能测试方法以多齿分度台为测试平台,在重力场试验环境下,通过连续数据采集方式获取一时间段内的加速度计输出信号,并利用样本熵和统计参数来定量分析加速度计的重力场模型参数及其变化情况。其中,所采用的奇异值分解方法考虑到了分度台测试中加速度信号与噪声干扰间的奇异特征值空间可分离特性,并通过矩阵空间重构方式实现信号降噪,从而达到提高采集信号质量的目的。所采用的总体最小二乘辨识算法考虑到了信号测量误差和加速度计安装角度误差问题,能够提高模型参数的辨识效果。统计试验说明,所采用测试方法能够有效描述加速度计模型参数的连续变化情况,可用于评价加速度计性能质量。

图4 门状态下K0系数曲线Fig.4 K0curves of lateral pendulum state

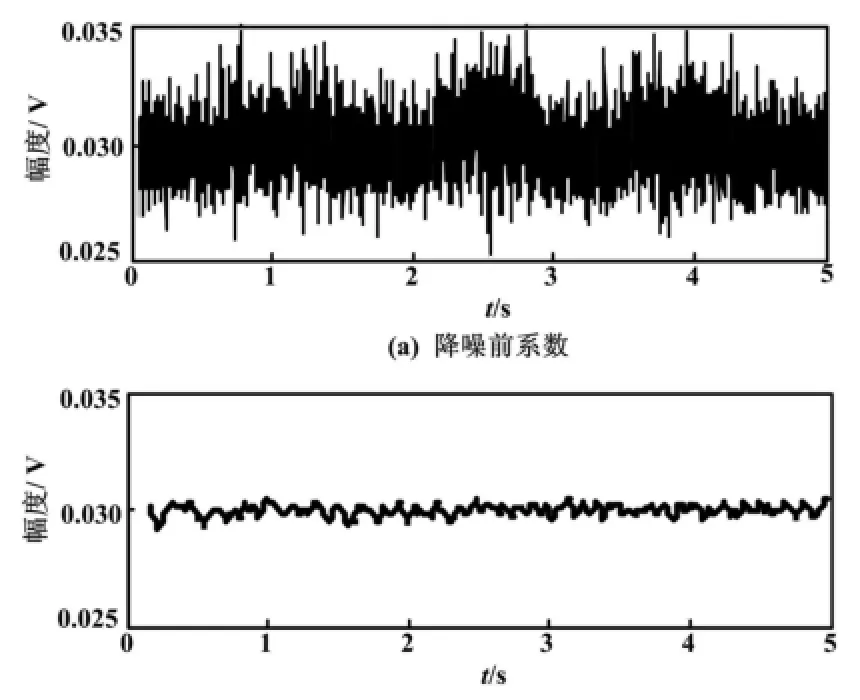
图5 门状态下K1系数曲线Fig.5 K1curves of lateral pendulum state

表1 摆状态下辨识系数统计结果Tab.1 Statistical results of recognition coefficients of horizontal pendulum state

表2 门状态下辨识系数统计结果Tab.2 Statistical results of coefficients of lateral pendulum state

3 结束语

利用奇异值分解、总体最小二乘、样本熵与统计参数,研究石英挠性加速度计的模型参数辨识方法及其评价问题。针对信号噪声干扰,采用奇异值分解技术分离出与加速度信号相对应的奇异特征值并重构出降噪信号。试验结果表明,利用原始采集信号辨识的系数受噪声影响较大且不稳定,而利用降噪信号辨识的系数稳定性较好。

此外,在应用统计参数评价的基础上,利用样本熵复杂度描述能够挖掘出加速度计内在的稳定性能变化情况。

[1] 严恭敏,李四海,秦永元.惯性仪器测试与数据分析[M].北京:国防工业出版社,2012:1-61.

[2] Xu D,Chen Y X,Kang R.Study of accelerated stability test method for quartz flexible accelerometer[J].IEEE Transactions on Device and Materials Reliability,2011,11(1):148-156.

[3] 任顺清,冯士伟,马向斌.加速度计的全组合标定方法[J].中国惯性技术学报,2007,15(6):760-764.

[4] 苏宝库,蒋效雄,刘雨.加速度计几种模型辨识方法的比较研究[J].传感器与微系统,2011,30(3):40-42,45.

[5] 何洪文,胡昌华,张伟,等.基于神经网络的加速度计静态误差系数标定[J].航空计测技术,2004,24(6):7-9.

[6] 于湘涛,张兰,陈格非,等.基于微粒群算法优化支持向量机的加速度计静态模型辨识[J].中国惯性技术学报,2010,18(3): 347-350.

[7] Zhou W,Li B L,He X P,et al.Calibration study of force-balanced micro accelerometer based on least squared method and genetic algorithm[C]∥Proceedings of the IEEE International Conference on Mechatronics and Automation,2009:1357-1361.

[8] 高贤志,蒋效雄,陈伟,等.一种基于半参数回归的加速度计误差模型辨识方法[J].中国惯性技术学报,2012,20(3):352-357.

[9] Eichstadt S,Link A,Bruns T,et al.On-line dynamic error compensation of accelerometers by uncertainty-optimal filtering[J].Measurement, 2010,43(5):708-713.

[10] Batista P,Silvestre C,Oliveria P,et al.Accelerometer calibration and dynamic bias and gravity estimation:analysis,design,and experimental evaluation[J].IEEE Transactions on Control Systems Technology,2011,19(5):1128-1137.

[11] Tian W,Wu S C,Zhou Z B,et al.High resolution space quartz-flexure accelerometer based on capacitive sensing and electrostatic control technology[J].Review of Scientific Instruments,2012,83(9):95-97.

[12] Hassanpour H,Zehtabian A,Sadati S J.Time domain signal enhancement based on an optimized singular vector denoising algorithm[J].Digital Signal Processing,2012,22(5):786-794.

[13] 张洪钺,黄劲东,范文雷.全最小二乘法及其在参数估计中的应用[J].自动化学报,1995,21(1):40-47.

[14] Markovsky I,Van S.Overview of total least-squares methods[J].Signal Processing,2007,87(10):2283-2302.

[15] Xie H B,He W X,Liu H.Measuring time series regularity using nonlinear similarity-based sample entropy[J].Physics Letters A, 2008,372(48):7140-7146.

[16] Molina A,Cuesta D,Aboy M,et al.Comparative study of approximate entropy and sample entropy robustness to spikes[J].Artificial Intelligence in Medicine,2011,53(2):97-106.

Singular Value Decomposition Filtering and Parameter Recognition of Accelerometer Signals

Aiming at the noise influence problem in model parameter recognition of quartz flexible accelerometer,by adopting the singular value decomposition technology,the filtering noise reduction for measured signal is implemented;then high quality recognition of model parameter is realized by combining the total least square algorithm.With the multi-tooth indexing bench under gravitational field as the test and analysis platform,the recognition effects are evaluated quantitatively by using sample entropy and statistical parameters.The experimental result shows that the noise interference in signals can be effectively eliminated by singular value decomposition technology,and the model coefficients obtained from denoised signals are stable.The method proposed effectively implements parameter recognition analysis for accelerometer,it can be used in performance quality evaluation.

Quartz flexible accelerometer Parameter recognition Singular value decomposition Total least square method Sample entropy

TP391

A

修改稿收到日期:2014-03-26。

李强(1982-),男,2008年毕业于中国科学技术大学生物医学工程专业,获博士学位,副教授;主要从事传感器信号检测与处理等方面的研究。