电子横移伺服LQR最优控制器设计

闻霞 吴龙 晋芳伟

(三明学院机电工程学院1,福建 三明 365004;三明机械CAD工程研究中心2,福建 三明 365000)

电子横移伺服LQR最优控制器设计

闻霞1,2吴龙1,2晋芳伟1,2

(三明学院机电工程学院1,福建 三明 365004;三明机械CAD工程研究中心2,福建 三明 365000)

为了提高系统的稳态精度和动态性能,将LQR最优控制算法应用于高速经编机电子横移伺服控制系统。建立了伺服系统状态空间模型,引入了一类具有指数衰减度的二次型函数作为系统性能指标。仿真结果表明,所提出的电子横移伺服LQR最优控制算法易于工程实现,保证了系统的稳定性,具有良好的频响特性,改善了系统的动态特性,实现了无静差高精度控制。

电子横移 伺服系统 线性二次调节器 最优控制 PID

0 引言

目前,带有电子横移系统的经编机能够实现高档、复杂、小批量的产品生产,优势明显[1]。进入21世纪,在电子送经系统成为当前国产经编机标准配置之后[2],进一步开发电子横移系统成为我国新一代经编数控技术的必然发展趋势。

近年来,在经编机电子横移系统的研究方面,国内已取得一些研究成果。文献[3]～[5]探讨了经编电子横移系统原理,建立了动力学模型,提出了硬件设计方案。文献[6]～[7]研究了采用直线伺服电机直驱横移机构的方法。

针对高速经编机电子梳栉横移的运动特点,采用改进PID算法相关的文献有[8]～[10]。

当前文献中所设计的基于PID的控制算法,已经无法满足经编伺服系统对系统稳定性、鲁棒性、高响应速度和高跟踪精度等系统性能指标的苛刻要求。本文给出了电子横移伺服线性二次调节器(linear quadratic regulator,LQR)最优控制算法,并通过仿真分析验证了算法的有效性。

1 经编机电子横移系统工作原理

由于直线伺服系统价格高昂,目前经编机电子横移系统主要采用旋转型交流伺服电机驱动梳栉横移机构。该系统一般主要由上位机、主控系统、伺服系统、机械传动机构和梳栉五部分构成,其原理如图1所示。

上位机一般由工控机和触摸屏构成,主要实现人机交互、生产过程监控、产品数据存储、网络管理、工艺参数修改和花型文件加载等功能。主控系统可由PLC或DSP、运动控制卡等组成,主要功能包括与上位机通信、接收经编机主轴信号以及计算并向伺服驱动器发送横移控制信号。伺服系统由伺服驱动器、伺服电机组成,用于驱动梳栉。机械传动机构主要由同步带传动机构、滚珠丝杆组成:同步带传动机构用于将伺服电机连接到滚珠丝杆,滚珠丝杆能将伺服电机的旋转运动化为直线运动,使梳栉进行有规律的往复、间歇式运动[11]。

2 伺服系统的数学模型

伺服系统是用来精确地跟随或复现某个过程的反馈控制系统,又称随动系统。在很多情况下,伺服系统专指被控制量(系统的输出量)是机械位移或位移速度、加速度的反馈控制系统,其作用是使输出的机械位移(或转角)准确地跟踪输入的位移(或转角)[12]。本文考虑采用结构如图2所示的交流伺服系统。

图2 伺服系统结构框图Fig.2 Structure of servo system

图2中:u为输入控制信号;ω为电机角速度;φ为输出信号(旋转角度);伺服电机惯量J=11.37 Nms2;系统增益K0=136.44 Nms。

2.1 伺服系统开环频域分析

式中:T为时间常数。

因为开环系统G0(s)为I型,闭环系统G1(j0)=1,根据带宽定义:

由图2可知,系统的开环传递函数为:

进而可求出系统开环截止频率ωc=0.996 rad/s,相角裕度γ=85.3°。由于开环截止频率过低,所以我们希望通过设计控制器,提高系统的开环截止频率。本文假定设计目标为(5～6)rad/s。

2.2 伺服系统状态空间描述

为了设计伺服系统的LQR控制器,需要进一步写出系统的状态方程。设x1=ω,y=x2=φ,x=[x1x2]T,代入参数J=11.37 Nms2,K0=136.44 Nms,则图2可转化为如图3所示的变量图。

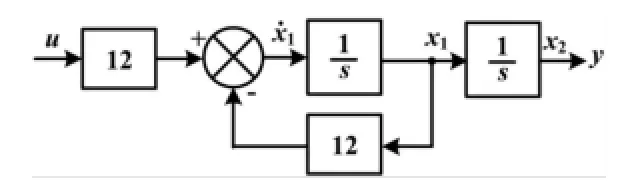
图3 伺服系统状态变量图Fig.3 State vector diagram of servo system

根据图3得到伺服系统状态空间表达式为:

3 线性二次型最优控制器(LQR)设计

3.1 LQR控制原理

对于线性时不变系统,可用下面一组方程来描述:

设线性系统的状态方程模型(A,B,C,D)已知,如果希望这样一个系统能够满足某种最优的要求,最简单的方法是引入线性二次型最优控制指标,即设计一个输入u(t),使得J最小。

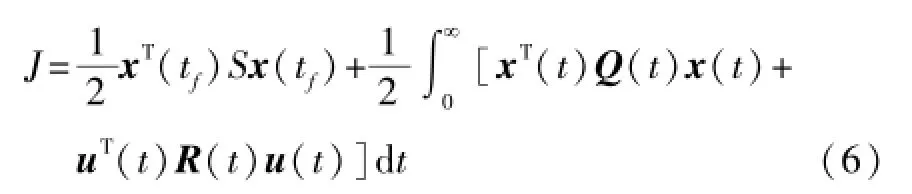
式中:tf为控制作用的终止时间;S为控制系统终值的某种约束;Q和R分别为对状态变量和控制变量的加权矩阵。

一般情况下,假定Q和R这两个矩阵是定常矩阵。为了使J最小,首先构造一个Hamilton函数:

若输入信号没有任何约束,则目标函数的最优值可以通过求解H矩阵对u的导数所构成的方程得出:

从而可以解出最优控制信号为:

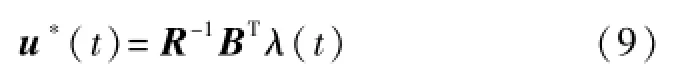
式中:λ(t)=-P(t)x(t);P(t)为对称矩阵,它是Riccati方程的解。

令tf趋于无穷,则P(t)趋于一个常值矩阵,P(t)的一阶导数趋于零,上述微分方程可简化为:

上式被称为代数Riccati方程,其求解就比较容易。因为该方程都是矩阵运算,用Matlab实现起来也比较容易。我们设计u*(t)=-Kx(t)的状态反馈,可得到闭环系统的状态方程,其可表示为:[(A-BK),B, (C-DK),D]。

3.2 LQR控制器的实现

在本例中,原经编伺服系统有一个极值点为0,属于不稳定系统。我们设计最优调节系统稳定且有指定的指数衰减度,使最优调节系统具有期望的指数稳定性。在这种控制策略中,系统的闭环极点均位于s平面s=-α的左侧,其中α＞0。此时性能指标函数描述为:

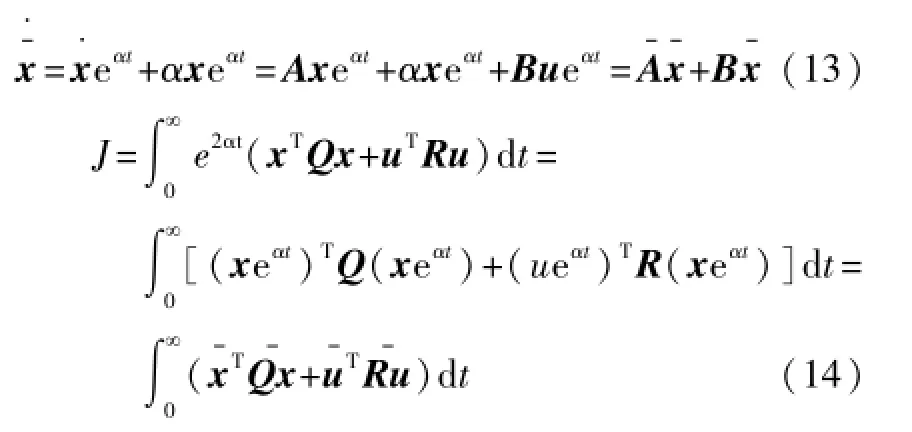
等价的Riccati代数方程为:P(A+αI)+(A+αI)TP+Q-PBR-1BTP=0。新的最优控制策略为u*(t)= -R-1×BTPx(t)。利用Matlab函数[K,P,E]=lqr(A,B,Q,R,N)可求得最优反馈矩阵K。该算法的目的是在一定的性能指标下,使系统的控制效果最佳,即利用最少的控制能量,来达到最小的状态误差。将K= [k1k2]代入到伺服系统(4)中,期望能保证系统稳定,并使得性能指标(12)最小。设r为参考输入,Kp为开环增益,加入反馈K=[k1k2]后伺服系统的状态变量图如图4所示。

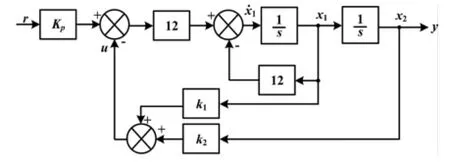
图4 基于状态反馈的伺服系统状态变量图Fig.4 State vector diagram of the servo system based on state feedback

设计LQR控制器的关键是选择加权矩阵Q和R。在实际系统允许的情况下,Q选择得越大,系统达到稳态所需的时间越短;而同样减小R,系统达到稳态所需的时间也就越短。目前确定加权矩阵Q和R的普遍方法是采用试凑的方法。该方法的基本原理是:首先进行分析初步选取Q和R,通过Matlab仿真判断其是否符合设计要求。如果符合要求,则停止仿真。下面是试凑法的几个一般原则。

①Q、R都应是对称矩阵,Q为正半定矩阵,R为正定矩阵。

②通常选用Q和R为对角线矩阵。实际应用中,通常将R值固定,然后改变Q的数值,最优控制的确定通常在经过仿真或实际比较后得到。当控制输入只有一个时,R成为一个标量数。

③Q的选择不唯一。这表明当得到的控制器相同时,可以有多种Q值的选择,其中总有一个对角线形式的Q。

④一般情况下,如果希望输入信号小,则选择较大的R矩阵,这样可以迫使输入信号变小;否则目标函数将增大,不能达到最优的要求。

通过判断,系统(4)能观能控,因此可以设计二次型最优调节器,并且使得闭环后的系统稳定。在设计前,首先对Matlab中专门求解连续系统线性二次型最优控制问题的函数lqr( )说明如下:lqr( )的调用格式为[K, P,E]=lqr(A,B,Q,R,N)。输入参数中,A为系统的状态转移矩阵,B为输入矩阵,Q为给定的半正定矩阵,R为给定的正的实对称矩阵,N为性能指标中交叉乘积项的加权系数矩阵。返回参数中,K表示最优反馈矩阵,P是Riccati方程P′+PA+ATP+Q-PBR-1BTP=0的解,E则是A-BK的特征值。

4 仿真结果分析

先将初始权矩阵设定为R=1、Q=diag(q1,q2)=diag(1,1),当运行程序后,得到校正前与校正后天线系统开环bode图和阶跃响应曲线,如图5和图6所示。校正后系统响应速度变差,并且稳态误差很大,需要进一步调节权矩阵Q(一般保持R不变)和增大开环增益Kp来优化系统。

当R=1时,调节权阵Q=diag(q1,q2)中的两个权系数q1和q2。在调试中我们发现q2对系统起到了积分作用,有助于消除静差,q1对系统起到了微分作用,有助于提高系统响应速度。经过试凑,使q1=q2=0.001,将开环增益设为6时,系统动态性能较好,截止频率提高到5.46 rad/s,相角裕度为65.9°,精度高、无静差。响应曲线如图7和图8所示。最优反馈矩阵为K=[0.003 1 0.031 6]。

图5 校正前后系统开环对数频率特性曲线[R=1,Q=diag(1,1)]Fig.5 Logarithmic frequency characteristic curves of open-loop system before and after correction[R=1,Q=diag(1,1)]

图6 校正前后系统的阶跃响应曲线[R=1,Q=diag(1,1),增益Kp=6]Fig.6 Step response curves of system before and after correction [R=1,Q=diag(1,1),Gain Kp=6]

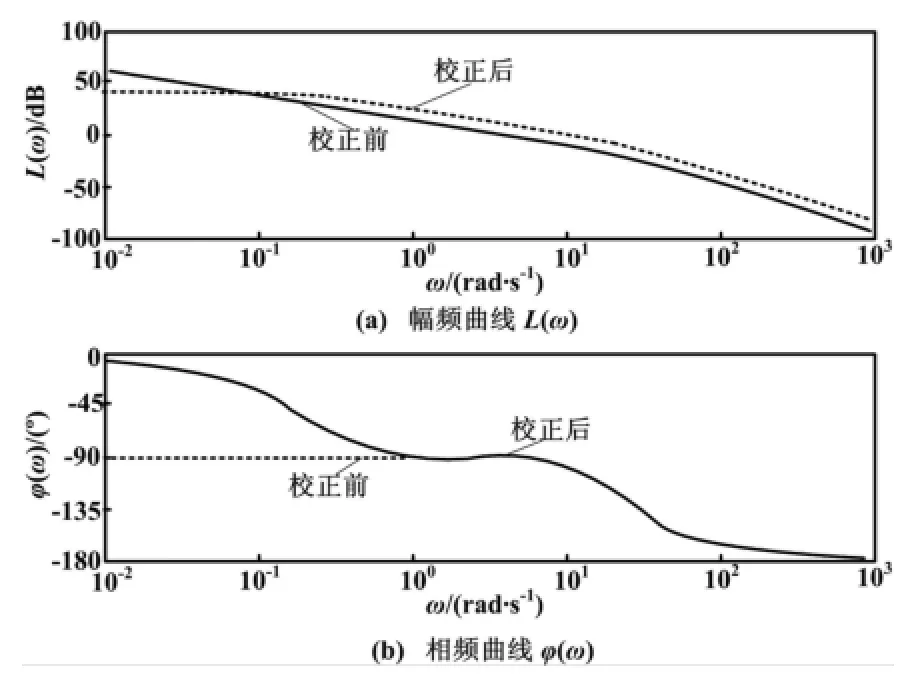
图7 校正前后系统开环对数频率特性曲线[R=1,Q=diag(0.001,0.001)]Fig.7 Logarithmic frequency characteristic curves of open-loop system before and after correction [R=1,Q=diag(0.001,0.001)]

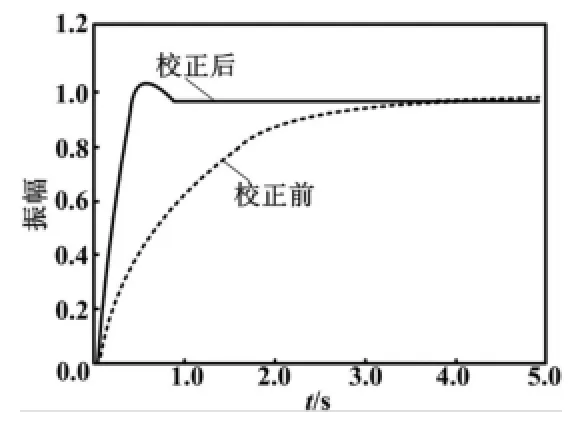
图8 校正前后系统的阶跃响应曲线(R=1,Q=diag(0.001,0.001),增益K″p=6)Fig.8 Step response curves of system before and after correction [R=1,Q=diag(0.001,0.001),Gain K″p=6]

5 结束语

本文介绍了经编电子横移系统的工作原理,分析了伺服控制系统模型的频域特性并建立了其状态空间描述。

针对高速经编机的特点,为了提高伺服系统的动态特性和跟随精度,提出了基于LQR的经编电子横移伺服最优控制器的设计方法。通过仿真算例验证了所提方法的有效性和正确性。

[1] 缪旭红,徐颖.EL型高速经编机的花型设计与产品开发[J].针织工业,2007(12):14-16.

[2] 任雯,胥布工.基于FI-SNAPID算法的经编机多速电子送经系统开发[J].浙江大学学报:工学版,2013,47(10):1712-1721.

[3] 孔震,蒋高明,夏风林.高速经编机电子横移原理探讨[J].针织工业,2007(9):12-14.

[4] 夏风林,蒋高明.基于DSP的经编机电子横移系统探讨[J].针织技术,2009(2):72-74.

[5] 周博,李平,金福江.经编机电子横移系统的模型参考自适应控制[J].上海电机学院学报,2013,16(3):117-124.

[6] 吴永春.经编机梳栉电子横移机构及控制方式的研究[J].机电技术,2011(5):52-54.

[7] 夏凤林.基于直线伺服控制的经编电子横移系统研究[D].无锡:江南大学,2010.

[8] 郑宝平,蒋高明,夏风林,等.双PID控制的经编机电子横移系统设计[J].纺织学报,2013,33(5):135-139.

[9] 殷明跃,夏风林,张琦,等.基于前馈控制的经编机横移系统高速定位[J].纺织学报,2011,32(11):126-130.

[10] 郑宝平,蒋高明,夏风林,等.基于转矩控制模式的经编电子横移系统设计[J].纺织学报,2012,33(10):122-127,140.

[11] 赵卫东,辛宏,王元,等.PLC在温度控制系统中的应用[J].仪器仪表学报,2001,22(04):469-470,478.

[12] 陈鹏展.交流伺服系统控制参数自整定策略研究[D].武汉:华中科技大学,2010.

Design of the Electronic Shogging Servo LQR Optimal Controller

In order to improve steady precision and dynamic performance of the system,the LQR optimal control algorithm is used in the electronic shogging servo control system of the high speed warp knitting machine.The state space model of servo system is established and the quadratic form function with exponential decay rate is introduced as the systematic performance index.The results of simulation show that the proposed electronic shogging servo LQR optimal control algorithm is easy for engineering implementation,and ensures the stability and better frequency response of the system,improves the dynamic characteristics of the system,and realizes high precision control without static error.

Electronic shogging Servo system Linear quadratic regulator(LQR) Optimal control PID

TP271+.4

A

福建省科技厅高校产学合作科技重大基金资助项目(编号:2011H6023、2012H6018)。

修改稿收到日期:2014-01-20。

闻霞(1980-),女,2007年毕业于新疆大学机械制造及其自动化专业,获硕士学位,讲师;主要从事机械设计制造及其自动化方面的研究。