电路参数调整的最优化方法研究

周婷 马海菊

(上海辰竹仪表有限公司,上海 201612)

电路参数调整的最优化方法研究

周婷 马海菊

(上海辰竹仪表有限公司,上海 201612)

针对电路调试工作复杂耗时的问题,提出了一种电路调试的参数最优化方法。首先采用拉氏变换建立电路的数学模型,然后利用数学规划的方法来调整电路参数,使电路达到理想的静态和动态指标。Matlab仿真结果表明,该方法是一种有效的计算机辅助设计方法。

参数调试 拉氏变换 数学规划 仿真设计 Matlab

0 引言

一个模拟电路在经过原理设计、PCB制版及元器件焊接后,其功能与设计时预设的功能存在一定的偏差。电子工程师不可能完全考虑到各种不确定因素,如元件值误差、器件参数的分散性和器件特性温漂等。因此,必须对样机进行测试和调整,使得电路达到预定的技术指标[1-2]。为了使电子工程师可以迅速把握整个电路的关键点,即调整少量的电子元件就可使整个电路达到满意的性能,本文引入了优化理论[1]。

优化理论提供了大量的实用方法来求解函数极值,已在电子电路、控制工程、通信等多个领域得到广泛应用[3]。优化理论所采用的数值方法可以很容易地处理多变量系统。如果能在电子元件数学模型的基础上,将问题转化为优化问题,则整个电路调试工作可由优化算法完成。模拟电路中,感性元件和容性元件的存在使整个电路成为一个动态系统,必须使用微分方程来描述。高阶微分方程的分析和综合是一个公认的复杂问题,关于它的研究,人们已经积累了丰富的经验。拉氏变换[4]就是一个专门用来分析微分动态系统的工具。其主要思想是变微分方程为代数方程,从而避免了复杂的求导和积分运算。

本文以拉式变换为工具,对模拟电路(主要是运放电路)进行建模、分析和设计,并利用Matlab软件完成了方法的实施。

1 电路调试中的优化方法研究

某工业用安全栅的部分电路如图1所示。该电路是一个四级运算放大电路,起着信号隔离和调理的作用。该电路的调试实践过程花费了大量的时间。本文所述方法就是在调试此电路的过程中形成的。

图1 某安全栅的信号调理电路Fig.1 Signal conditioning circuit of an IS barrier

1.1 电路建模

模拟电路常以运算放大器为核心进行设计。而运放的外围器件只有少量的电容电阻,其结构相对简单。这种特点使我们可以建立电路的数学模型,并用数学的方法来分析电路。

模拟电路中的基本元件有电阻、电容、电感等,它们分别对电流信号起着缩放、微分和积分运算的作用。为了简化运算,本文使用拉氏变换方式对单个元件进行建模。

为了得到运放电路输入输出方程,采用节点电流法[4]方程组,并配合放大器虚短特性,求解方程组即可得到输入输出函数。

例1:如图1所示,定义基准电压u8、u9、u10、u11、u13。根据节点电流法列写方程:

虚短路方程为:

解代数方程可由Matlab符号运算函数solve得到,解得此运放的传递函数为:

代入数值得到:

得到单个运放电路的传递函数后,经过级联就可以得到整个电路的传递函数:

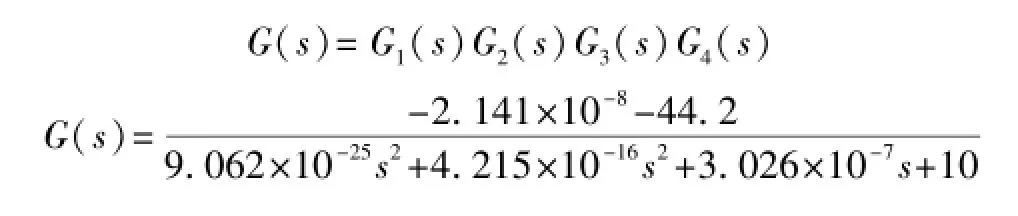
1.2 电路分析

电路调试分静态调试和动态调试两种。

静态调试一般是指在只加固定的电平信号的条件下所进行的直流测试,可用万用表测出电路中各点的电位,通过和理论估算值比较,结合电路原理的分析,判断电路直流工作状态是否正常,及时发现电路中已损坏或处于临界工作状态的元器件。通过更换器件或调整电路参数,使电路直流工作状态符合设计要求。

动态调试是在静态调试的基础上进行的,在电路的输入端加入合适的信号,按信号的流向,顺序检测各测试点的输出信号。若发现不正常现象,应分析其原因,并排除故障,再进行调试,直到满足要求。由此,电路的性能指标也分为静态指标和动态指标两种。静态指标有直流精度、输入阻抗、输出阻抗和功耗等。交流指标有交流精度、纹波、相位滞后等。

Matlab控制系统工具箱提供了丰富的函数用来分析系统特性[5]。dcgain函数可以计算电路的直流增益;bandwidth函数可以计算带宽;bode函数可以用来画出此电路的幅值衰减曲线和相位滞后曲线。

例2:使用Matlab控制系统工具箱计算电路的直流增益和带宽。图2为此电路在各频率输入信号下的幅值衰减和相位滞后。

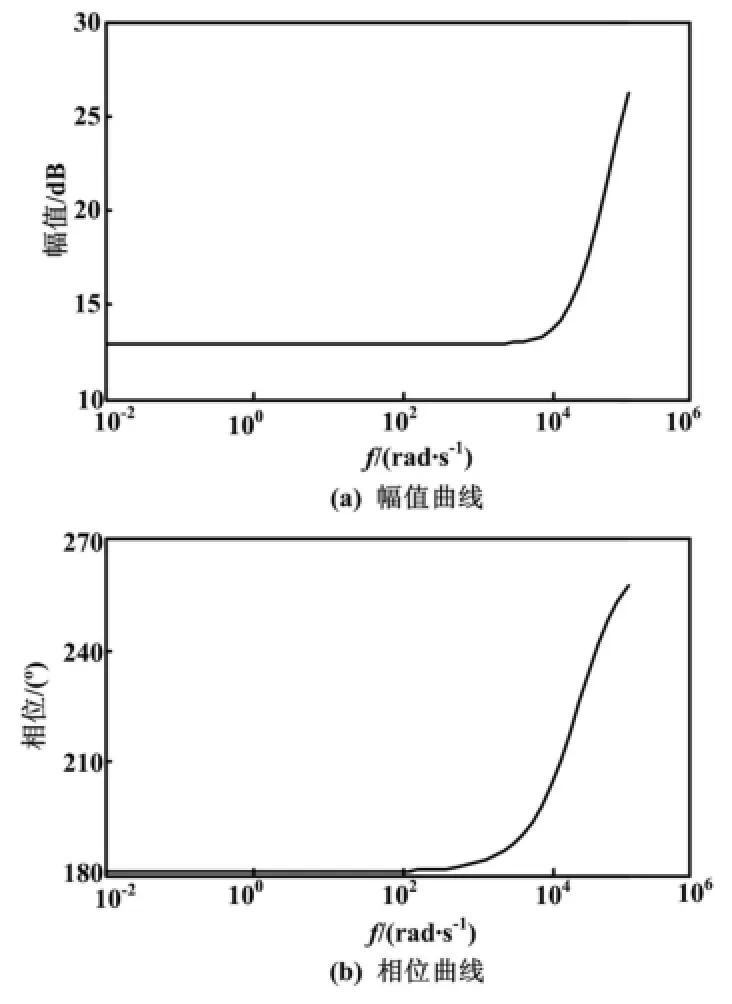
图2 放大电路的幅相曲线Fig.2 Amplitude-phase curves of amplification circuit

1.3 参数优化

不管是静态指标还是动态指标,它们都可以被看作是电路中所有电子元件的函数,即在性能指标和电子元件值之间存在这样的映射(α2,…,αk)=f(c2,…, cm,R2,…,Rn)。电路调试工作就可以理解为:为达到寻找一组合适的电容c1,…,cm和电阻R1,…,Rn,以得到期望的性能指标α2,…,αk。考虑到此函数一般为包含微分方程的非线性函数,我们便可以将此问题转化为以下非线性整数规划问题:

式中:p1,p2…为性能指标的期望值;C为电容的可行值集合;R为电阻的可行值集合。

在实践中,应该尽量多地加入约束条件,如电阻的功率约束、运放的输出电压约束等都应该考虑在内。

按此非线性规划问题的结果选择电路中元件的值,整个电路的性能指标在理论上接近所期望的性能指标。

调整电路参数,使运放电路G2达到以下性能指标:直流增益α=-3,频带宽度β=2×103。

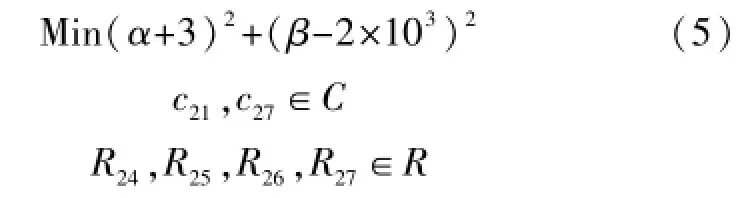
式中:C、R为国家标准规定的电阻电容标准值。

直流增益和频带宽度的计算方法如前节所述。此非线性规划问题由Matlab优化工具箱中函数fmincon完成[6],所得结果为:R24=1 kΩ、R25=100 kΩ、R26= 33 kΩ、R27=100 kΩ、c21=1 nF、c27=1 pF。

最终所达到的性能指标为:直流增益α=-3.018 2,频带宽度β=2.000×103。由于电子元件值的离散性,并没有得到准确的期望值增益。

1.4 微调电路

按上节方法便可以得到电路的基本参数。由于电阻电容的标准值是离散的,所以并不能准确地得到我们想要的直流增益。在样机完成后,常常会发现所得指标与期望值不符合。这是由于很多电子元件并不精确,而且有漂移等现象。因此,还需要微调电路元件值以达到理想效果。常见方法是调整电位器的输出以改变电路性能。这个调整可描述为以下迭代过程:

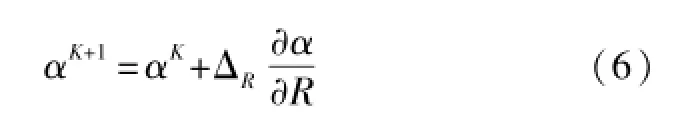
由此可以看到选择元件进行微调电路性能有以下两个原则。

①微调对某一性能指标相关的元件,也就是∂c不为零。

②微调对性能指标较敏感的元件,即选取∂α/∂R。例如,当调整两个电阻都可以改变某一运放的直流增益,而其中一个电阻只需要较小的改变,就可以带来较显著的增益变化,那么就优先调整这个电阻,使得效率最大。

根据原则①,我们可以很容易地找到应该调整哪些元件可以达到目的;然后根据原则②,就可以确定调整哪个元件以最小的调整量达到目的。

当我们为微调运放电路的直流增益而改变某一电阻的值,电路的直流增益和带宽都会随之变化。这时,就要尽量避免调整电阻值,否则会使电路越调越乱。

2 结束语

本文描述了基于数学模型的模拟电路分析和调试方法。拉氏变换是一种将微分运算转化为代数运算的方法,常用来对动态过程进行建模。由于运算放大器电路只有少量的电阻和电容外围器件,使我们用复变换建立较为简单的输入输出方程成为可能。方程的阶次由容性元件的个数决定。整个建模过程可由Matlab符号运算完成。在运放电路输出方程的基础上, Matlab提供了大量的动态系统分析函数,可以很容易地得到电路的静态增益、带宽、幅相曲线等性能指标。本文还探讨了将电路调试问题转化为非线性规划,利用最优化工具箱来进行电路参数自动调试的方法。

刚进入电子电路设计领域的工程师具备良好的数学基础而缺乏对物理对象的实际理解,采用优化的方法来解决电路参数调试问题正好可以扬长避短。随着商业化的计算机辅助设计软件的大量涌现,如Matlab、Mathmatica,新一代的电子工程师必须学会利用这些先进工具为自己服务。

而对于公司研发平台建设而言,通过逐步积累各种电路优化算法,并与仿真软件相结合,将相应的数学模型固化,推广应用于实际研发过程。该优化方法对于提高研发效率和研发质量,均可取得了较好的效果。

[1] 李士军,郭学全.浅析单边带电路的调试[J].信息技术,2002(3): 21-23.

[2] 吕俊霞,李炜恒.电子设备电路的调试方法与技巧[J].印刷电路信息,2007(6):55-58.

[3] 姚恩瑜.数学规划与组合优化[M].杭州:浙江大学出版社, 2001:100-198.

[4] 邱关源.电路[M].北京:高等教育出版社,2006:56-66.

[5] 刘叔军.Matlab7.0控制系统应用与实例[M].北京:机械工业出版社,2006.

[6] 曹卫华,郭正.最优化技术方法及MATLAB的实现[M].北京:化学工业出版社,2005.

Research on the Optimization Method of Circuit Parameter Adjustment

A parameter optimization method for circuit debugging is presented to solve the problems of complexity and time-consuming in circuit debugging jobs.Firstly,the Laplace transform is used to establish the mathematical model of the circuit;then the parameters of circuit are adjusted by adopting mathematical programming method to make the circuit reach ideal static and dynamic indexes.The results of Matlab simulation indicate that this method is an effective computer aided design method.

Parameter debugging Laplace transform Mathematical programming Simulation design Matlab

TM135

A

修改稿收到日期:2014-04-26。

周婷(1977-),女,1999年毕业于浙江大学能源专业,获学士学位,高级工程师;主要从事工业仪表、防爆技术、功能安全技术及研发平台的研究。