旋转变压器信号的标定与解调

张健

(青岛农业大学机械电子工程学院,山东 青岛 266109)

旋转变压器信号的标定与解调

张健

(青岛农业大学机械电子工程学院,山东 青岛 266109)

针对检波后信号存在直流偏置、幅值不等和相位偏移等问题,采用梯度估计算法,对检波后的包络信号进行离线标定;并设计了基于状态观测器的旋转变压器-数字转换(RDC)算法,对标定后的包络信号进行解调。试验结果表明,梯度估计算法收敛速度快,估计精度高。与反正切法相比,所设计的RDC算法不需通过数值差分即可获得角速度信息,干扰抑制能力强,角位置和角速度估计精度高。

旋转变压器 伺服传感器 梯度估计 角速度估计 最小二乘法

0 引言

针对旋转变压器检波后信号通常存在直流偏置、幅值不等和相位偏移的问题,常采用的标定方法有:峰-峰值检测法[1]、神经网络法[2]、Heydemann法[3-4]。其中,峰-峰值检测法未考虑相移,神经网络法在实际应用中受限制。本文在Heydemann法的基础上,利用梯度估计法替代最小二乘法,对检波后信号进行补偿。

旋转变压器常用解调方法有反正切法[5-7]和角度跟踪法[8-10]。反正切法由于差分运算的引入,角速度误差较大。角度跟踪法具有一定滤波作用,抗干扰能力强,但在信号频率快速变化时仍存在一定的估计误差。本文设计了基于状态观测器的解调算法。该算法能同时估计出转子角位置和角速度信息,避免了差分运算对噪声的放大作用,对模型不确定性及干扰有较强的适应性,且实现容易。

1 旋转变压器工作原理

目前,常用的无刷旋转变压器由旋转变压器本体和附加变压器两部分组成。

施加在附加变压器源绕组上的励磁信号为:

通过电磁耦合,信号将传递至旋转变压器本体的转子绕组。若励磁频率ωex远高于转子电角频率ωe,旋转变压器副绕组的输出信号可近似描述为励磁信号与转子电角位置θe正余弦值的乘积,即:

式中:k为旋转变压器变压比;E为励磁信号幅度;θm为转子角位置;p为极对数。

2 基于梯度估计的检波后信号标定

实际应用中,由于受众多非理想因素(如旋转变压器的机械构造、电路不对称)的影响,旋转变压器检波后的包络信号并非理想的完全正交信号,而是存在直流偏置、幅值不等和相位偏移。检波后信号可描述为:

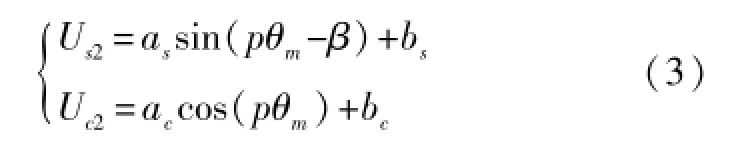
式中:as、ac为增益系数;β为相位偏移;bs、bc为直流偏置。

此时若直接对信号进行解调,必将造成较大的误差。可先通过离线方式求取式(3)中的各未知量,进而对包络信号进行补偿。

式(3)可改写为:

设:

取目标函数为:

对式(9)求导,整理可得:

设η为大于零的常数,取:

则有:

3 基于状态观测器的信号解调算法

设经补偿、整定后的旋转变压器包络信号为:

设转子角位置θm及角速度ωm可表示为:

式中:δ(t)为未建模动态,假定其为有界信号。

以式(13)为量测方程、式(14)为状态方程,可以设计状态观测器对转子角位置θm及电角速度ωm进行观测。状态观测器的基本形式为:

式中:kθ、kw、ka为状态观测器增益系数。

将式(8)在坐标原点处线性化,可得状态方程为:

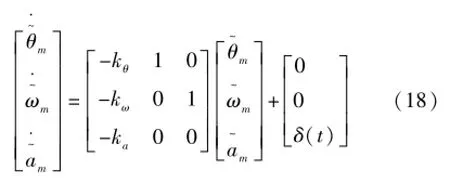
线性化后,系统的雅克比矩阵为:

取kθ、kω、ka均大于零,且kθkω＞ka,则A的特征值均具有负实部。根据李雅普诺夫第一方法,误差方程式(17)在原点处是渐进稳定的。为便于计算机实现,以Ts为采样周期,可将式(17)离散化为:

4 试验结果及分析

为验证本文方法的有效性,进行了试验验证。在试验装置中,伺服传感器及电动机部分由A、B两伺服电机同轴连接,其中A电机装有有效位数可达20位的高精度光电码盘,B电机装有极对数p=4的旋转变压器。驱动与控制板以TMS320F28335为CPU,完成对光电码盘及旋转变压器输出信号的解调及伺服电机的驱动。

光电码盘解调方式为M/T法,旋转变压器检波方式为乘积检波,可近似认为利用光电码盘所获取的角位置及角速度信息为真值信息。该信息可作为旋变解调信息准确性的判断依据。

试验过程分3个步骤进行。

①离线获取检波后包络信号

驱动伺服电机旋转,利用DSP记录一段时间内的旋转变压器包络信息。由于DSP的A/D转换电压范围为0～3.3 V,所以对检波后的包络信号采用硬件电路,增加了直流偏置。

②获取补偿校正参数

利用步骤①所记录的包络信号,根据前述的标定算法,离线计算未知的不对称参数。此过程可通过DSP或者Matlab实现。本文采用DSP实现。计算所得参数为:X=[-1.334 1 0.174 0 1.024 1 -1.031 5 0.949 7]T。

X各元素迭代收敛过程如图1所示;补偿校正前后的李沙育波形如图2所示。

图1 向量X各元素迭代收敛过程图Fig.1 Convergence process of each element of vector X

由图2不难看出,采用梯度估计算法能够很好地对包络信号的直流偏置、幅值不等和相位偏移进行补偿。

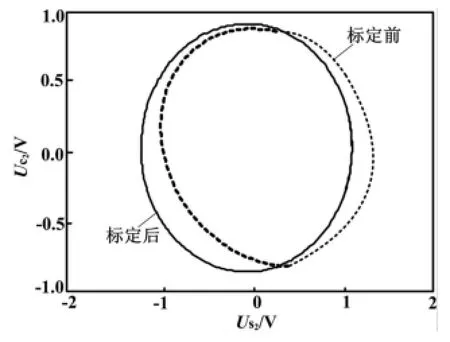
图2 补偿校正前后两路信号的李沙育图形Fig.2 Comparison of Lissajous figures before and after compensation correction

③角位置及角速度在线解调性能测试

控制伺服电机按照一定形式的速度旋转,根据步骤②所得参数,按照式(8)对采集所得的包络信号进行修正。然后,采用前述的基于状态观测器的解调方法对其解调,获取角位置及角速度,并与利用光电码盘所获取的角位置及角速度信息相减,得到角位置及角速度误差。为验证解调算法的有效性,本文分别对匀速、匀加速、正弦速度3种情况进行了试验。

图3～图4为电机以ωm=628 rad/s匀速旋转时,两种解调算法的角位置及角速度误差曲线。图5～图6为电机以ωm=100t rad/s匀加速旋转时,两种解调算法的角位置及角速度误差曲线。图7～图8为电机以ωm= [628+ 62.8sin(2πt)]rad/s正弦形式速度旋转时,两种解调算法的角位置及角速度误差曲线。

对于角位置的解调误差,观测器法均优于反正切法;而对于角速度解调误差,除正弦速度情况下,其他速度形式均优于反正切法一个数量级。

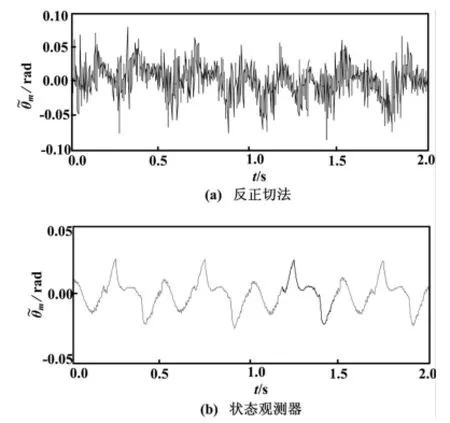
图3 电机匀速运转时角位置误差曲线Fig.3 Angular position error curves under motor constant speed operation

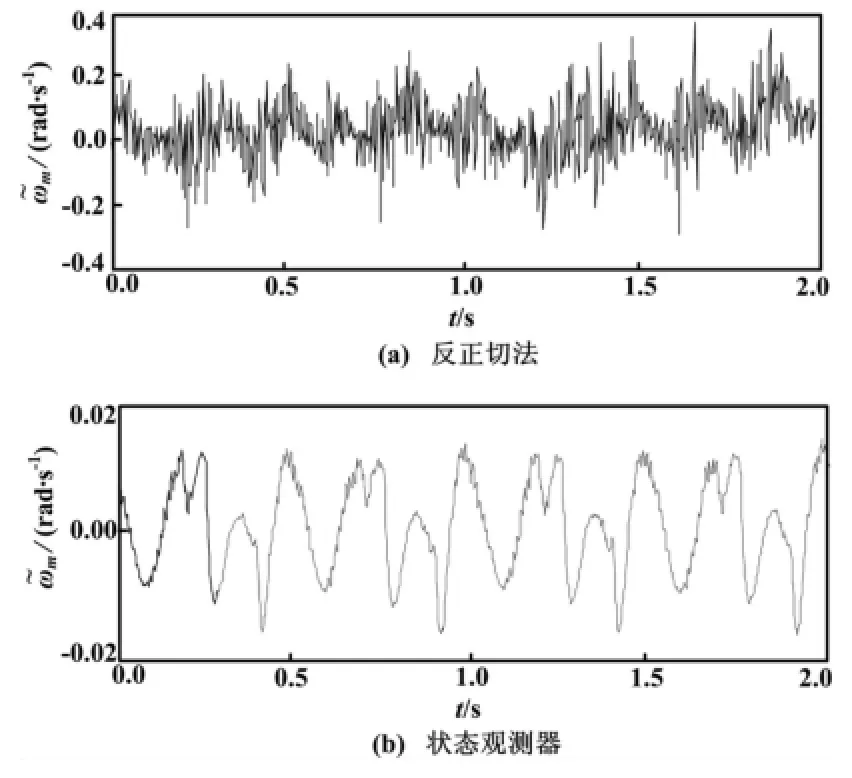
图4 匀速运转时角速度误差曲线Fig.4 Angular velocity error curves under constant

图5 匀加速运转时角位置误差曲线Fig.5 Position error curves under constant acceleration

图6 匀加速运转时角速度误差曲线Fig.6 Speed error curves under constant acceleration

图7 正弦速度运转时角位置误差曲线Fig.7 Position error curves under sine speed

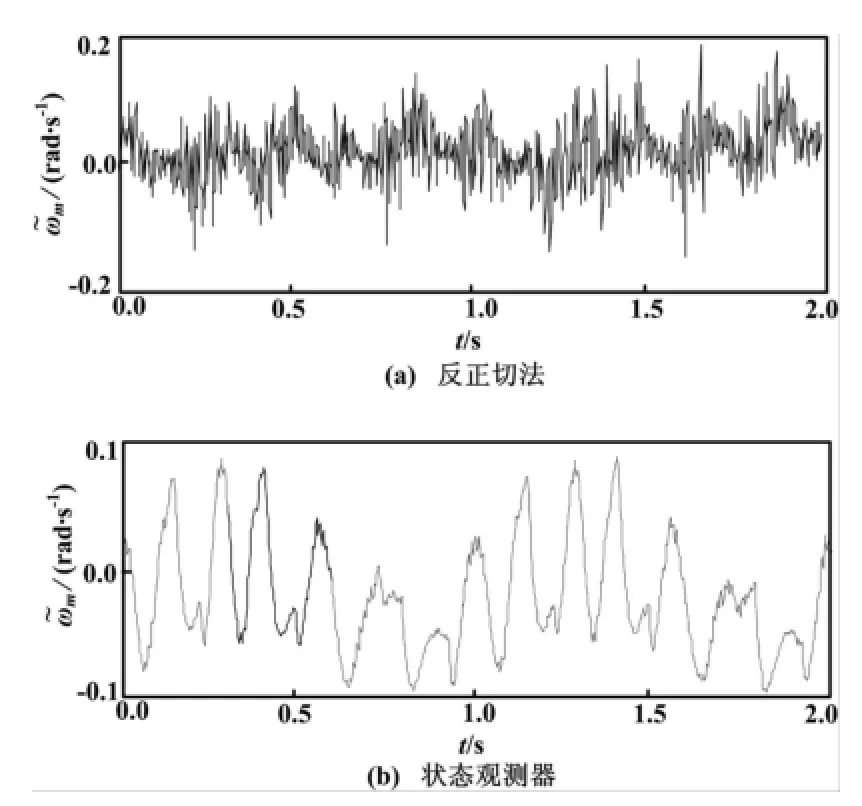
图8 正弦速度运转时角速度误差曲线Fig.8 Speed error curves under sine speed

5 结束语

本文针对正余弦旋转变压器输出检波后的包络信号,首先通过梯度估计算法进行补偿,然后利用基于状态观测器的RDC算法,对补偿后信号进行解调。理论推导及试验结果表明,所采用梯度估计算法能够很好地解算出包络信号中的直流偏置、幅值不等和相位偏移;基于状态观测器的RDC算法,不需通过数值差分即可获得角速度信息,避免了差分运算对噪声的放大作用,角位置及角速度解调精度明显高于反正切法。此方法具有一定的实用价值。

[1] Mayer J R.High-resolution of rotary encoder analog quadrature signals[J].IEEE Transactions on Instrument and Measurement,1994,43(3):94-498.

[2] Tan K K,Tang K Z.Adaptive online correction and interpolation of quadrature encoder signals using radial basis functions[J].IEEE Transactions on Control Systems Technology,2005,13(3):370-377.

[3] Heydemann P L.Determination and correction of quadrature fringe measurement errors in interferometers[J].Applied Optics,1981,20(19): 3382-3384.

[4] Tan K K,Zhou H X,Lee T H.New interpolation method for quadrature encoder signals[J].IEEE Transactions on Instrument and Measurement, 2002,51(5):1073-1079.

[5] Hagiwara N,Suzuki Y,Murase H.A method of improving the resolution and accuracy of rotary encoders using a code compensation technique[J]. IEEE Transactions on Instrumentation and Measurement,1992,41(1): 98-101.

[6] Hoseinnezhad R,Harding P.A novel hybrid angle tracking observer for resolver to digital conversion[C]//44th IEEE Conference on Decision and Control,European Control Conference,Piscataway: IEEE,2005:7020-7025.

[7] Choong Y,Joong H,Myoung K.A resolver-to-digital conversion method for fast tracking[J].IEEE Transactions on Industrial Electronics,1992,39(5):369-378.

[8] Seon H H,Hyun J K,Jang M K,et al.Compensation of amplitude imbalanceandimperfectquadratureinresolversignalsfor Permanent Magnet Synchronous Motor drives[J].IEEE Transactions on Industry Applications,2011,47(1):134-143.

[9] Idkhajine L,Prata A,Monmasson E,et al.System on chip controller for electrical actuator[C]//IEEE International Symposium on Industrial Electronics,Piscataway:IEEE,2008:2481-2486.

[10] Harnefors L,Nee H P.A general algorithm for speed and position estimation of AC motors[J].IEEE Transactions on Industrial Electronics,2000,47(1):77-83.

Calibration and Demodulation of Resolver Signal

To against the problems of detection signals of resolver,e.g.,DC bias,amplitude deviation and phase shift,by using gradient estimation algorithm,the envelop signal after detection is calibrated offline,the resolver to digital conversion(RDC)algorithm based on state observer is designed for demodulating the envelop signal after detection.The result of experiments indicates that the gradient estimation algorithm features fast convergence speed,high estimation accuracy.Comparing with the arctangent method,the RDC algorithm proposed is able to obtain information of angular velocity without numerical differential operation,and features high capability of eliminating interference, and high accuracy for estimating angular position and angular velocity.

Resolver Servo sensor Gradient estimation Angular velocity estimation The least square method

TM383

A

修改稿收到日期:2013-10-21。

作者张健(1982-),男,2006年毕业于山东科技大学测试计量技术及仪器专业,获硕士学位,讲师;主要从事伺服电机控制的研究。