考虑CO2排放量的城市专业物流中心选址研究

赵泉午，杨 茜

（1.重庆大学经济与工商管理学院，重庆400030；2.重庆大学公共管理学院，重庆400030）

考虑CO2排放量的城市专业物流中心选址研究

赵泉午1，杨 茜2

（1.重庆大学经济与工商管理学院，重庆400030；2.重庆大学公共管理学院，重庆400030）

目前关于物流中心选址的研究多基于企业的角度，鲜有学者站在地方政府角度考虑不同行业物流特点对城市物流中心选址进行研究。本文基于钢材分销行业特征，从地方政府角度出发，构建了综合考虑CO2排放量和物流成本的双目标整数规划模型，采用理想点法将双目标转化为单目标并用分枝定界法对该模型进行求解。本文以重庆市钢材分销行业的城市物流中心选址为例进行分析，并将CO2排放量的测算结果以澳大利亚碳税的征收标准进行计算，发现碳税征收并不能有效降低钢材行业CO2排放量。地方政府可通过合理选择物流中心位置、规范城市物流配送车辆选型、限速、限行和错峰限时等城市物流管理策略来实现低碳物流。

CO2排放量；城市物流；物流中心选址；钢材分销

1 引言

为了实现物流的时间效益和空间效益，提高物流过程的运作效率，许多城市纷纷提出了对物流网络体系进行优化的举措。据不完全统计，目前全国发布和完成现代物流网络体系规划研究工作的经济中心城市已超过50个，主要分布在珠三角、长三角等东南沿海及北方沿海区域经济中心城市。同时，学术界有关城市物流网络体系的研究也日渐丰富，物流网络的设计一般包括两个方面［1-3］：一是物流网络体系中物流节点位置和数量的确定；二是优化分配各个线路上的物流配送量。而物流节点选址作为物流网络体系优化的基础与核心，往往也作为单独的研究对象，其模型建立在配送量确定的前提下，仅将物流节点选择作为决策变量建立整数规划模型进行研究［4-7］。

早期，有关物流节点选址的研究主要集中在单一目标成本最小。Aikens等［4］基于目标函数为“选址成本（包括固定投资成本和运输成本）最小”，建立线性规划、0-1整数规划和动态规划等9种选址模型对物流网络优化中的节点选址进行了对比研究，得出不同的规划模型形式主要是取决于选址费用函数的形式。周根贵等［5］也建立一个基于物流成本最小的选址模型，引入机会成本（短缺）、处置成本（过剩）、期望成本，更加详细的描述了物流过程的成本，并使用遗传算法对该模型进行求解，从而得出了回收中心的选址和最优规模。

现实中不同决策者不单单追求物流成本最小单一目标，还考虑路径最短、对交通的拥堵的影响最小、以及环境污染最小等因素；同时物流节点选址问题也会涉及到对不同主体的利益的考虑——比如地方政府、企业和居民，而每一个主体注重的选址要素也会有所差异。因此越来越多的学者开始考虑不同主体多因素目标对物流节点选址的影响。陈菊等［6］基于地方政府的物流总成本最小和企业运输的效用值最大选择物流节点，建立了一个双层物流节点选址模型，并使用遗传算法对该模型进行求解，得到了物流中心选址的最优方案。胡长英等［7］将物流过程中的环境因素考虑进来，通过政府对产品环境不达标程度的处罚成本和企业在政府要求下主动处理污染的成本来度量环境因素，从而建立了一个考虑环境影响与物流成本的双层、双目标物流节点选址方案，并提到该模型可以使用遗传算法、分支定界算法以及启发式算法等来求解。

综上现有对物流节点选址的研究，从过去的仅仅只考虑经济因素，逐渐转向了对经济与环境因素的共同考虑，而且越来越注重对环境因素的关注；而现有研究往往将环境影响简单抽象为排污成本［7-8］，或者抽象为概念性的参数，缺少具体科学应用。本文在现有研究基础上，将二氧化碳排放量引入到物流节点选址模型中。

物流很大程度上依赖于交通运输，交通运输又将产生大量二氧化碳对环境造成污染，根据IEA 2009［9］的统计，在世界范围内，交通运输过程中排放的二氧化碳量是其总排放量的26%，仅次于占比第一的能源生产二氧化碳排放量。Ballot和Fontane［10］以法国为例探索供应链变化对二氧化碳排放量的影响，并分别选择公路和铁路两种运输系统，基于二氧化碳排放量最少目标建立模型，得出了最优供应链网络的选择方案。Figliozzi［11］也以美国波特兰市为例，讨论运输过程中影响二氧化碳排放的因子，发现拥挤和限速对二氧化碳排放量有显著的影响，并认为公共机构应该规范物流中心的选址和车辆运行速度，从而能够很好的减少二氧化碳排放量。因此本文将二氧化碳排放量引入到物流网络节点选址优化模型中，同时量化城市物流中心选址的经济与环境因素，站在地方政府的角度，并考虑配送厂商的现实选择——配送路径相对最短、成本相对最低，建立一个基于CO2排放量和物流成本的双目标整数规划模型，并给出双目标规划的求解方法。另外，鉴于不同行业配送方式和物流中心选址要求的差异，本文以重庆市钢材分销城市物流中心选址优化为例进行详细的分析。

2 模型的建立与求解

2.1 问题的描述

钢材分销城市物流一般包括三级：一级是货运站场，是指火车货运站和港口码头；二级是物流中心，是指钢材分销专业市场；三级是需求节点，是指工业园区、规划的人口聚集区和建筑工地（交通、市政工程等基础设施建设）等对钢材有需求的节点。运输车辆从货运站场将货物运送到物流中心，然后运输车辆又将货物从物流中心运送到各需求节点，货物的供需关系和流动情况将形成了一个完整的物流配送网络结构（如图1所示）。货运站场和需求节点的数量和位置是固定的，物流中心的数量和位置在备选点中选出。其选择依据是两个目标函数，即满足从货运站场到需求节点过程中的CO2排放量和物流成本达到最优的状态。

2.2 假设条件

为了方便分析和说明问题，对模型进行了如下的假设和简化：

（1）由货运站场到物流中心、由物流中心到需求节点之间的运输距离是已知的，返回时的路径与配送时的路径是一致的。

（2）优化后的物流中心数量是有限的。城市物流中心的数量受限于城市规划及土地资源供给。

（3）各需求节点的需求量是可以预测的。

（4）城市内的道路等级分为两级，不同的道路等级，车辆运行的速度不同。

（5）货车运输成本、单位商品的仓库成本均为已知的。

2.3 参数和变量定义

i指货运站场，N表示i的数量；

j指物流中心，M表示j的数量；

k指需求节点，L表示k的数量。

dij指从i到j的运输距离（公里）；

djk指从j到k的运输距离（公里）。

图1 模型示意图

Xij指从i到j的货运量（万吨），Xij≥Dj*wj*λ，Dj表示j点的总需求量（出量Dj=，λ表示配送货运量的临界值（即配送货运量的下限比例），j=1，2，3……M；

Xjk指从j到k的货运量（万吨），Xjk≥Dk*wj*λ，Dk表示k点的总需求量，λ同上，k= 1，2，3……L。

wj是指备选物流中心是否被选中的决策变量，wj∈{0，1｝，当j点被选中，wj=1；反之取0。

根据《MEET and COST 319 European projects》［12］中的研究得到：εempty（v）是空车运输过程中二氧化碳排放量系数，εfull（v）是满载车辆运输过程中二氧化碳排放量系数，它们的单位为克/公里，φ（r，v）则表示空车与满载车辆在运输过程中二氧化碳排放量的差异比；当考虑卡车容量WC（万吨）和卡车运行速度V（公里/小时）时，ε（Xij，Wc，v）则表示每公里运输量为X（万吨）、卡车容量为WC、车速为V的运输过程中二氧化碳的排放量（克/公里），是指递送的次数。它们的关系式表达如下：

其中：K，a，b，c，d，e，f为为CO2排放量与速度之间的关系系数；

c1指单位距离（公里）的货车空车时的运输成本（万元）；

c2是指单位距离（公里）单位货物（万吨）的货车运输成本（万元），其中i到j和j到k使用的货车类型相同；

c3指单位货物（万吨）在物流中心（j点）的库存成本（万元）。

P1为CO2排放量函数，其单位是克。P2为物流成本函数，其单位是万元。

2.4 数学模型

目标函数：

min F={（P1），（P2）｝

其中，CO2排放量函数：

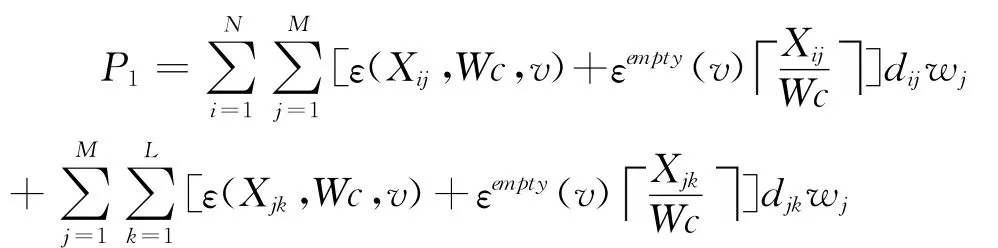
物流成本函数：

2.5 求解方法

多目标规划模型的求解思路往往是先将多目标转化成单一目标，而决策者在将多目标转化为单一目标的过程中往往采用两种方式，其一是附权重，即根据各目标彼此的重要程度给予不同的权重，然后予以加总，从而转化成单目标规划；其二是考虑优先顺序，该方式也是需要决策者先确定各目标的重要性，从而决定每个目标的优先程度，即越重要的目标先被考虑，后面的目标都需要在满足前面目标的前提下运行。而常常具体使用到的方法有：线性加权、指数加权、理想点法、主要目标法、分层序列法和模糊偏差法等。在这些方法中，线性加权、指数加权和理想点法往往要求目标函数的单位是一致的，本文中的目标函数分别是CO2排放量（克）和成本（万元），因此需要通过比例的方式把两个目标的单位转成一致，然后再对两个目标进行整合。所以本文将对理想点法进行改进来解决这一双目标问题。

理想点法：先求出每个单目标的最优解P*，再令，将它作为新的目标函数进行求解。

改进后的理想点法：先求出每个单目标的最优解P*，再令，将它作为新的目标函数进行求解。

同时在模型中也可以看出唯一的变量是wj，是指备选物流中心是否被选中的决策变量，其取值为wj∈{0，1｝，当wj=1时，j点被选中；反之取0时，j点未被选中。这也正是0-1整数规划恰恰可以数量化的描述“取与舍、有与无”等现象所反映的离散变量间的逻辑关系，正好可以解决这类问题。在目标函数达到最优的时候，用整数变量表示各种选择，连续变量表示资源的分配，用约束条件表示物流的平衡关系。其核心思想是将每一个物流中心纳入目标函数中进行计算、比较，最后再决定是否需要该物流中心。而0-1整数规划的解法有很多种，比如穷举法，隐枚举法、组合直接搜寻法等；其统计分析软件也有许多，比如Matlab、Lingo［13］、Mathematical等。本文将选取Lingo11.0分析软件进行求解。

3 实例分析

本文以重庆市钢材分销行业为例，对未来重庆市钢材城市配送的物流网络进行优化设计。根据《重庆市国民经济与社会发展第十二个五年（2011-2015年）规划纲要》，重庆市未来主要的钢材货运站场有团结村、黄磏站和鱼嘴-果园港三大货运站场；而未来钢材的主要需求节点则主要是12大工业园区和22个人口聚集区；根据规划，本文选出金材物流果园配送中心、中钢国际钢材交易中心、西部金属材料物流配送中心、赫乾鑫邦钢材城、攀宝钢材市场、珞磺钢材交易城、重庆铁公鸡钢铁物流港、重庆永翔钢铁贸易服务总部基地八大物流中心作为备选的物流中心。

本文提供的钢材需求量是2020年的预测需求量，根据2002-2011年的钢材需求量数据采用回归预测法、二次加权移动平均预测法、GM（1，1）预测法以及组合预测法对重庆市2012-2020年钢材的市场需求量进行预测，并根据工业用钢和建筑用钢的比例对不同钢材需求节点用钢情况进行划分，再结合工业园区的面积和人口聚集区的人口比例得出了12大工业园区和22个人口聚集区在2020年具体的钢材需求情况。

本文统计了3个货运站场到8个备选物流中心的运输距离；同时统计了8个备用物流中心到34个需求节点的运输距离。根据《中华人民共和国公路法》，按照其技术等级分为高速公路、一级公路、二级公路、三级公路和四级公路。其流量和速度标准如表1所示：

表1 不同公路等级的时速限制

根据这一标准，将重庆市主城区钢材配送的车辆路径分为两个等级，一个是时速控制在60-120公里/小时的一级路段，其包括高速公路和一级公路两种路段；其二是时速在60公里/小时以下的二级路段，其包括二、三、四级公路；运输距离统计结果如附录表3和表4所示。

根据《MEET and COST 319 European projects》［12］的研究，当货车的载重在32-40吨之间时，CO2排放量的公式系数结果测量为：

K=1576，a=-17.6，b=0，c=0.00117，d= 0，e=36067，f=0，φ（r，v）=1.42；

可知在市内运输钢材的货车载重一般在30吨以上，因此取Wc=0.0033万吨；在一级路段的运行速度V1=60公里/小时，在二级路段的运行速度为V2=40公里/小时；另外，根据调研数据，设参数c1=0.00025万元/公里，c2=0.5万元/公里/万吨，c3=50万元/万吨。则P1和P2为：

目标函数则为：

通过Lingo11.0的计算，得出了仅仅只考虑CO2排放量、仅仅只考虑物流成本和综合考虑两个因素的双目标模型的结果。如表2和表3所示：

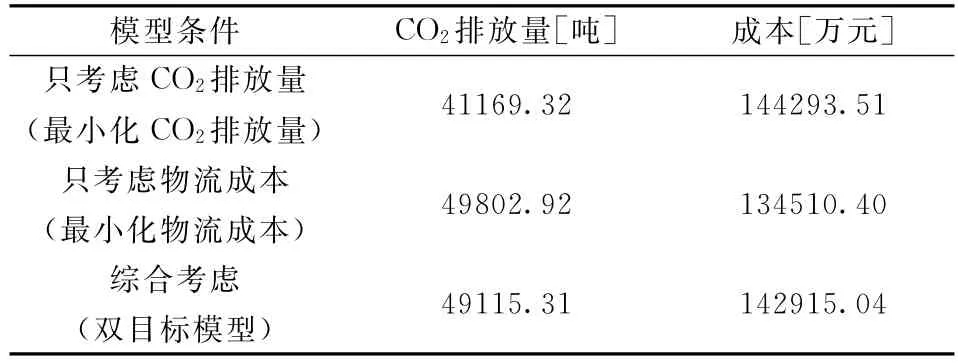
表2 不同模型条件下的CO2排放量和成本的比较

表3 不同模型条件下物流中心的选择

在表2中可以看出，综合考虑物流成本和CO2排放量的物流中心选址方案比单纯考虑成本的物流中心选址方案每年物流成本增加了6.24%，但CO2排放量却减少1.38%；比单纯考虑CO2排放量的物流中心选址方案每年CO2排放量增加19.30%，但是物流成本减少0.95%。可以发现构建的双目标模型具有较好的综合优势，使得CO2排放量和物流成本得到比较均衡的结果，综合考虑了物流中心选址优化过程中的经济与环境因素。同时，综合考虑的双目标模型与只考虑CO2排放量的单目标模型相比，减少物流成本1378.47万元，因此综合考虑的选择更加满足企业降低物流成本的现实需求。

从表3中可以看出，珞磺钢材交易城、重庆永翔钢铁贸易服务总部基地两个物流中心在不同的模型条件下都会成为最优的节点；该两个物流中心一南一北分布，而且都靠近钢材货运站场。珞磺钢材交易城靠近黄磏站，重庆永翔钢铁贸易服务总部基地靠近鱼嘴站-果园港，交通运输条件十分便利。这样的选址结果也比较符合市场需求和交通运输条件。

同时，根据澳大利亚2012-2013年的碳税征收标准：每吨碳排放征收23澳元，折合人民币133.26元/吨（2013.10.13日的汇率，1澳元=5.7941人民币元）。则征收的碳税如表4所示：

表4 不同模型条件下物流中心选择的社会成本比较

通过对比以澳大利亚碳税标准征收碳税后的结果可以发现，综合考虑的双目标模型和只考虑CO2排放量的社会成本总和并不低于只考虑物流成本选址方案的总成本，这说明按照这一标准征收碳税并不能够很好的限制企业运输过程中的CO2排放量。但从不同条件下选址结果的对比和CO2排放量函数中可知，政府可以通过采取合理选择物流中心位置、选择并规范配送车辆车型、限速、限行和错峰限时等城市物流管理策略来控制CO2排放量，实现低碳城市物流目标。

最后，根据目标函数和Lingo11.0的计算，企业最优选择节点和节点之间具体配送量也可以算出。综合考虑CO2排放量和物流成本时得出的各条路径上的配送量是政府平衡环境与成本后的结果，但现实中企业往往是从物流成本最低或配送时间最短选择配送路径，因此实际的路径配送量与本文结果可能存在差异。消除差异的重要举措就是实施限速、限行、错峰限时配送以及合理选择城市物流车型等城市物流管理举措。

4 结语

本文在城市物流中心选址过程中引入了CO2排放量，充分考虑了物流中心的社会与环境效益，并考虑钢材分销物流行业的特征，建立了基于CO2排放量和物流成本的双目标整数规划模型，使得物流中心的利益受众综合考虑环境与经济效益两个目标。同时本文引用了重庆市钢材分销物流中心选址的案例，采用Lingo编程方法对该问题快速科学的求解，得出了重庆市钢材分销物流中心综合考虑CO2排放量和物流成本的最优选址结果，也对比了综合考虑两个目标和单独考虑两个目标的选址差异。案例数据充分，结果合理，是模型可行性的有力证明，对地方政府进行物流选址的优化设计具有很好的参考借鉴价值。

本文不足在于仅仅针对具体的某一行业对城市物流中心的选址进行了分析，事实上不同行业物流差异较大，未来研究可以考虑整合不同行业从而得出综合型物流中心的选址结果；同时未来可研究城市物流管理举措对城市物流成本和CO2排放量的影响。

［1］代颖，马祖军，刘飞.基于混合遗传算法的制造/再制造集成物流网络优化设计［J］.计算机集成制造系统，2006，12（11）：1853-1875.

［2］石琴，陈朝阳，覃运梅.多目标物流网络优化模型的研究［J］.中国管理科学，2005，13（4）：40-43.

［3］冯勤超，顾宁生.逆向物流网络优化设计模型［J］.东南大学学报（自然科学版），2007，33（11）：321-326.

［4］Aikens C H.Facility location models for distribution planning［J］.European Journal of Operational Research，1985，22（3）：263-279.

［5］周根贵，曹振宇.遗传算法在逆向物流网络选址问题中的应用研究［J］.中国管理科学，2005，13（1）：42-47.

［6］陈菊，何美玲，牟能治.物流节点最优选址与规模的双层规划模型［J］.物流商坛，2006，29（129）：9-13.

［7］胡长英，刘国山.基于环境角度的双层选址优化模型［J］.中国管理科学，2007，15（4）：59-62.

［8］何波.绿色物流网络系统建模与效率边界分析［J］.中国管理科学，2012，20（3）：138-144.

［9］International Energy Agency.2010能源技术前景［R］. http：//www.iea.org/.

［10］Ballot E，Fontane F.Reducing transportation CO2 emissions through pooling of supply networks：Perspectives from a case study in French retail chains［J］. Production Planning&Control，2010，21（6）：640-650.

［11］Figliozzi M A.The impacts of congestion on time-definitive urban freight distribution networks CO2 emission levels：Results from a case study in Portland，Oregon［J］.Transportation Research Part C，2011，（19）：766-778.

［12］Joumard R.Methods of estimation of atmospheric emissions from transport：European scientist network and scientific state-of-the art action COST 319 final report［M］.Bron：INRETS，1999.

［13］丁小东，姚志刚，程高.lingo语言与0-1混合整数规划选址模型的再结合［J］.物流工程与管理，2009，31（10）：72-75.

［14］Munuzuri J，Cortés P，Grosso R，et al.Selecting the location of minihubs for freight delivery in congested downtown areas［J］.Journal of Computational Science，2012（3）：228-237.

［15］Pan S，Ballot E，Fontane F.The reduction of greenhouse gas emissions from freight transport by pooling supply chains［J］.International Journal of Production Economics，2010，10：1-9.

［16］Ubeda S，Arcelus F J，Faulin J.Green logistics at Eroski：A case study［J］.International Journal of Production Economics，2011，131（1）：44-51.

［17］Byrka J，Aardal K.An optimal bifactor approximation algorithm for the metric uncapacitated facility location problem［J］.SIAM Journal of Computing，2006，39（6）：2212-2231.

［18］Kayikci Y.A conceptual model for intermodal freight logistics centre location decisions［J］.Procedia Social and Behavioral Sciences，2010，2：6297-6311.

［19］O'Connor K.Global city regions and the location of logistics activity［J］.Journal of Transport Geography，2010，18：354-362.

［20］Chen C T.A fuzzy approach to select the location of the distribution center［J］.Fuzzy Sets and Systems，2001，118：65-73.

The Location of City Professional Logistics Centers on Consideration of CO2Emissions

ZHAO Quan-wu1，YANG Xi2
（1.School of Economics and Business Administration，Chongqing University，Chongqing 400030，China；2.School of Public Affairs，Chongqing University，Chongqing 400030，China）

Plenty papers study logistics center location problems based on the perspectives of enterprises. While few scholars consider impacts of local government and logistics characteristics of different industries.Based on the logistics characteristics of steel distribution industry，a dual-objective integer-programming model is constructed both considering CO2emissions and logistics costs，which represents the opinions of local government.Then doubles goals model are turn into a single one model by ideal point method. The logistics center location problems of Chongqing steel distribution industry is taken as an example，and the results of logistics center locations are obtained through collecting and computing the real data from Chongqing steel distribution industry.At last tax of CO2emissions is calulated based on the standard of carbon tax in Australian.Results show that tax of CO2could not reduce CO2emissions effectively.Local government should adopt other City logistics methods to control CO2emissions effectively，such as reasonable location of logistics center，vehicle selection，speed limit，time windows and so on.

CO2emissions；city logistics；logistics center location problems；steel distribution industry

C939；F207

A

1003-207（2014）07-0124-07

2013-07-29；

2013-10-22

国家自然科学基金青年项目（71002070）；重庆大学中央高校基本科研业务费（CQDXWL-2012-Z019）；教育部人文社会科学研究项目（09YJC630244）

赵泉午（1976-），男（汉族），河南方城人，重庆大学经济与工商管理教授，复旦大学博士后，硕士生导师，CLEMSON大学和香港中文大学访问学者，研究方向：现代物流与商贸流通管理、区域经济与发展.