我国农村土地间接流转供应链联盟的利益分配机制研究——基于“对称互惠共生”视角

温修春，何 芳，马志强

（1.江苏大学管理学学院，江苏镇江 212013；2.同济大学经济与管理学院，上海 200092；3.江苏大学土木工程与力学学院，江苏镇江 212013）

我国农村土地间接流转供应链联盟的利益分配机制研究
——基于“对称互惠共生”视角

温修春1，3，何 芳2，马志强1

（1.江苏大学管理学学院，江苏镇江 212013；2.同济大学经济与管理学院，上海 200092；3.江苏大学土木工程与力学学院，江苏镇江 212013）

利益分配是供应链联盟的一个共同而关键的问题，制订公平合理的利益分配方案对供应链联盟的成功运作无疑是重要的。本文从“对称互惠共生”的视角，按照生产要素贡献分配利益的原则，首先采用柯布-道格拉斯生产函数确定各生产要素（劳动、土地和资本）贡献率，然后，对人力资本要素（劳动）建立相应的博弈模型并给出了在利益相关者之间的最优分配解，而对于非人力资本要素则按其投入比例进行分配，最后，通过算例求解得到了农户、中介组织和种植企业在土地流转中获得的最优综合分配额。本文研究结果不仅对农村土地间接流转，而且对其他生产商与供应商之间的供应链合作利益分配机制的建立也具有指导意义。

农村土地；间接流转；供应链联盟；利益分配；对称互惠共生

1 引言

近年来，我国农村土地承包经营权流转市场出现了一种新型的土地流转模式——“中介参与的间接式”。土地间接流转是指通过土地流转经营中介组织为媒介进行的土地流转活动，如土地银行（土地信用合作社）、土地信托机构、土地储备机构、农村集体经济组织等等。根据我国各地区的农村土地流转实践来看，我国专业化从事土地流转的第三方组织主要有以下三类：第一类是以四川彭州市、宁夏平罗县等为代表的“土地银行”；第二类是以浙江绍兴县、湖南益阳市等为代表的“土地信托服务机构”；第三类是以江苏常州市、浙江平湖市等为代表的“土地股份合作社”。由于它们均承担着土地流转中介服务的功能，因此，本文将这些组织统称为“中介组织”。

事实上，根据浙江大学农业现代化与农村发展研究中心和浙江省农业厅联合调查组的调研报告显示，浙江省的土地流转中，共有3069个中介服务组织参与，农地流转中介服务组织的数量占村数量的比例为7.8%，同时，浙江省农地流转面积达到300亩，占全省总耕地面积的12.4%，其比例在全国名列前茅［1］。由此可见，中介组织在农村土地流转过程中发挥的作用非同一般。对此，刘莉君［2］也比较分析了直接式、政府参与的间接式和中介参与的间接式三种农村土地流转模式的绩效，得出中介参与的间接式是最优的。然而，关于农村土地间接流转联盟利益分配的研究文献极少，即使是关于其他供应链联盟中的利益分配问题，绝大多数文献也只是在非对称共生关系的前提下来研究的，但这并没有达到“帕累托最优”的状态。根据共生理论，对称性互惠共生是共生系统进化的基本方向和根本法则，同时，对称性互惠共生状态也是最佳激励兼容状态或称最佳资源配置状态［3］。因此，促进对称性互惠共生关系的形成是任何共生系统（包括农村土地流转）发展的必然要求。鉴于此，本文从对称互惠共生模式的角度出发，试图研究我国农村土地间接流转供应链联盟的利益分配机制，以此为我国农村土地间接流转实践提供理论指导。

2 我国农村土地流转供应链利益相关者的共生关系

2.1 非对称的互惠共生关系

张颖聪、张文秀［4］指出在土地流转市场中，农户、农村集体经济组织、中介组织和业主或经济组织等土地使用者产生的关系，具备构成委托代理关系的条件；李怀、高磊［5］认为农户签订土地承包合同后，因为具备了土地的转让权，所以既可以选择自主经营，亦可以选择委托其他组织或个人经营，在农地流转中进一步形成委托代理关系；同样，许艳［6］也指出农户、农村集体经济组织（笔者注：类似中介组织）和非农业主之间存在着契约关系、信息不对称和利益结构不一致，三者之间确实存在着委托代理关系。由此可见，在我国农村土地间接流转过程中，农户、中介组织与种植企业之间的关系实质上是一种委托代理的关系，而且还是一种双重委托代理的关系，不仅农户与中介组织之间存在着委托代理关系，同时中介组织与种植企业之间也存在着委托代理关系。正是由于他们这种各自所处的地位不对等，因而他们之间的利益分配机制往往表现为非对称性，即一方攫取另一方的经济剩余。因此，此时他们三者之间的非对称互惠共生关系可用图1表示：

图1 我国农村土地间接流转主体间的非对称共生关系

2.2 对称的互惠共生关系

在现实中，由于各联盟成员彼此之间的依赖程度不同，各自所处的地位也将不同，所以大多数的共生关系均表现为非对称互惠共生。然而，在所有系统中对称性互惠共生系统是最有效率也是最稳定的系统，任何具有对称性互惠共生特征的系统在同种共生模式中具有最大的共生能量，任何具有非对称性互惠共生特征的系统在同种模式中，关键共生因子分配的非对称性越小则具有越大的共生能量［7］。继此之后，卓颖、蔡运隆等［8］进一步研究得出，共生单元处于正向对称共生状态（即共生单元的共生度相等且均大于0）时，共生能量达到最优分配，能量损耗最小，是最理想的共生状态。另外，在新古典生产理论中，存在着一个虚拟的厂商，这个虚拟的厂商决定生产过程中需要使用劳动和资本的数量，并将劳动和资本投入到生产过程中，得到一定数量的产品，称为“厂商模型”［9］。据此，本文假设农户、中介组织和种植企业以对称互惠共生模式存在，而且在农村土地流转中也存在这样一个“公正”的虚拟厂商，使得投入该供应链联盟的各生产要素之间不存在雇佣关系，既非“资本雇佣劳动”也非“劳动雇佣资本”，亦不存在任何一方攫取另一方的经济剩余。因此，可用简单示意图来表示各联盟成员之间的对称互惠共生关系（如图2所示）：

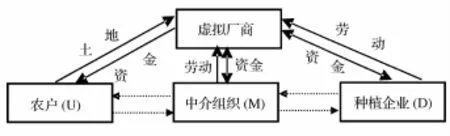
图2 我国农村土地间接流转主体间的对称共生关系

Thorton和Tuma［10］认为，供应链联盟没有固定的边界，组织间的关系可能发生断裂、重组，而导致联盟网络不断变化和扩展。这样，从理论上来说，农村土地流转供应链联盟由非对称的链式联盟演变为对称的网络状联盟完全是有可能的。

3 对称互惠共生供应链联盟利益分配的总体原则

在对称互惠共生的网络状联盟中，各联盟成员之间又该如何来分配利益呢？江泽民同志在党的十五大报告中提出“把按劳分配与按生产要素分配结合起来，鼓励资本、技术等生产要素参与收益分配”。之后，党的十六大又提出了“劳动、资本、技术和管理等生产要素按贡献参与分配的原则”。实质上，按生产要素贡献参与分配是对以往分配方式的继承与发展，标志着对我国收入分配制度的探索又达到一个新的理论高度。由此可见，按生产要素贡献参与分配是我国当前及未来一定时期内的主要收入分配制度。另外，对于虚拟企业（供应链联盟）的利益分配研究，赵忠华、王晓华［11］认为，“要素价值的确定是利益分配的基础，而分配要素价值的确定又要根据参与分配要素的特点和在虚拟企业中所起的作用来确定。”

因此，本文针对我国农村土地间接流转过程中，农户、中介组织和种植企业在组建对称互惠共生的联盟之后，各联盟成员之间按生产要素贡献原则分配利益，较好地贯彻了“效率优先，兼顾公平”的社会主义收入分配原则。由于按生产要素分配是生产要素所有权或占有权在经济上的实现，即凭借要素所有权或占有权获取收益［12］，所以又设农户是土地要素的占有者（或所有者），中介组织和种植企业则为资本要素和劳动要素的所有者。

4 测度参与合作的生产要素贡献率

纵观历史，关于生产要素贡献测度的研究，最早由克拉克（John Bates Clark）创立的边际生产力分配理论和由马歇尔（Alfred Marshall）创立的供求均衡分配理论均从边际量上测度劳动和资本（包括土地）要素的份额与贡献。至20世纪20年代，美国数学家柯布（C.W.Cobb）和经济学家道格拉斯（Paul H.Douglas）又创立了生产函数理论，即称为柯布-道格拉斯生产函数（Cobb-Douglas production function），从总量上测度劳动和资本要素的份额及贡献；后来，索洛（Robert Merton Solow）又发现了生产函数模型的“余值”现象，于是，就又引入了丁伯根（Jan Tinbergen）提出的“全要素生产率”的概念，用以说明技术进步的贡献。

因此，本文在借鉴前人的研究基础上，对我国农村土地间接流转供应链联盟中各生产要素贡献的测度时，引入修正的柯布-道格拉斯生产函数的一般形式：

F（K，H，L）=Y=AKχHγLϑ（1）

其中，Y为总产出量，参考国内大多数学者的做法以及本文的研究内容，选用农户、中介组织与种植企业合作的总收益值作为总产出量；A为全要素生产率，常常被视为科技进步水平的指标；K为资本投入量；H为劳动力投入量，对此国内外学者常用投入的劳动力人数作为劳动投入量指标，然而，在理论上，劳动投入量是指实际投入的劳动量，应该用有效的劳动时间来反映，而有效的劳动时间不仅取决于劳动的投入数量，还取决于劳动的利用效率与劳动的质量等多种因素［13］；L为土地投入量；χ、γ、ϑ分别为资本、土地和劳动产出的弹性系数。

首先，对公式（1）两边取自然对数进行线性变换，则可得：

其次，对公式（2）两边求微分，可得：

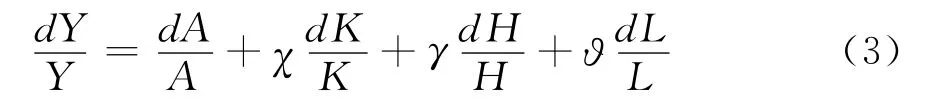
其中，dY/Y表示总产出增长率，dA/A表示全要素生产率增长率，d K/K表示资本要素增长率，d H/H表示劳动要素增长率，d L/L表示土地要素增长率。

再将（2）式分别对A，K，H，L求偏导数，并整理得：

其中，∂Y/∂A，∂Y/∂K、∂Y/∂H和∂Y/∂L的经济学意义分别是：在现有的生产条件下，当其他生产要素比例保持不变时，每增加一个单位全要素、资本、劳动和土地所引起的总产出的增加，即它们对农业生产总产出的贡献，其在数量上相当于各生产要素的纯收益。

然后，再引入生产函数要素分析方法，则可建立各生产要素与产出的函数关系式（即各生产要素贡献率）：

又通常实际测算用差分代替微分，则式（3）可转化为：

于是，资本增长、劳动增长和土地增长对总产出增长的贡献率则分别为：

因此，式（5）可被式（7）所替代。

而全要素的平均增长率（即全要素生产率增长率）常用“索罗余值法”计算，即由式（6）可得：

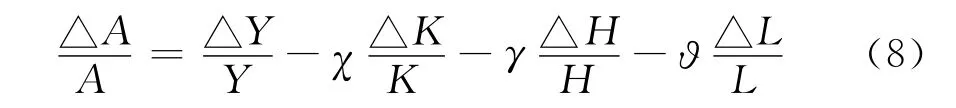
那么，全要素增长对总产出增长的贡献率为：

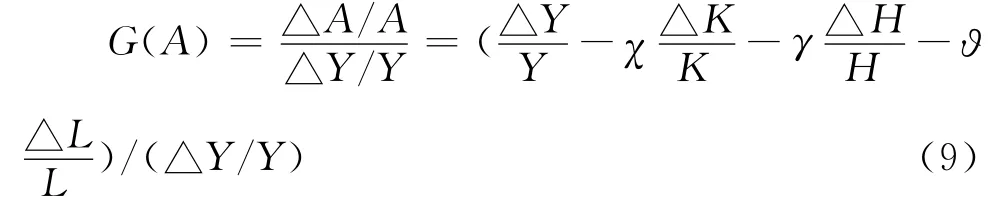
正如前文所述，按生产要素分配是凭借要素所有权或占有权来获取收益的，然而，农户、中介组织和种植企业都不是全要素的所有者或占有者，因此，本文对全要素对总产出的增长率按资本、土地和劳动要素贡献率的比例进行分配，则资本增长、土地增长和劳动增长对总产出增长的贡献率分别转化为：

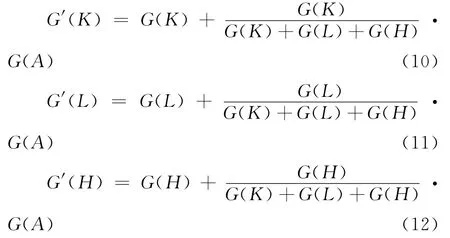
5 我国农村土地间接流转供应链联盟的利益分配方案

周其仁［16］将企业（笔者注：本文中的虚拟厂商）视为“人力资本和非人力资本的一个特别市场合约”，而人力资本（劳动要素）与非人力资本（土地、资金和技术要素等）存在本质的区别：其一，非人力资本与其所有者在自然形态上具有可分离性，可以在不同的所有者之间相对容易地转移，而人力资本则做不到这点，而且根据周其仁［16］的研究表明，不管在什么样的社会中，人力资本与其所有者不可分离的状况都是无法改变的；其二，人力资本所有者不仅拥有显性人力资本，还有隐性人力资本，而非人力资本则相对易观察。基于人力资本与非人力资本的差异性，故本文按照人力资本与非人力资本分类进行要素贡献分配收益，并且假设土地流转后的总产出为F（K0，L0，H0）=Y0。

5.1 因人力资本要素贡献的分配

5.1.1 基本模型的构建

根据前文的假设，中介组织和种植企业为土地流转供应链中的劳动要素所有者，因此，设g1和g2分别表示中介组织和种植企业的工作努力水平；η1和η2分别表示中介组织和种植企业工作的贡献系数（其大小取决于该成员的核心能力的独特性和相对重要性）；ρ1和ρ2分别表示中介组织与种植企业的工作创新性活动成本系数，则他们的工作努力总成本函数为：C（ρ1g1，ρ2g2），且满足：∂C/∂g1＞0，∂2C/∂2g1＞0，∂C/∂g2＞0，∂2C/∂2g2＞0；又设总劳动收益为R（η1g1，η2g2），π为中介组织和种植企业合作的净劳动收益，则有：

为研究问题的方便，不失一般性，我们可以进一步假设，中介组组织与种植企业的工作努力总成本以及总劳动收益分别为努力水平的二次函数和线性函数，则有：

其中，θ为中介组织与种植企业之间工作的关联系数，但为了使生产函数具备Hyers-Ulam稳定性，故此假设θ=0；C0为常数，表示固定成本（或陷入性成本）；ξ为随机干扰变量，且服从正态分布，即ξ～N（0，σ2）。这里，值得特别说明的是，各函数式中加系数是为了后面运算化简的方便，可以通过对开方计入成本系数而将各函数式的系数化为1，并不影响各变量之间的函数关系。

将上述式（14）、（15）代入式（13）可得：

一般而言，常见有三种利益分配模式：产出分享模式、固定支付模式和混合模式［17］，但结合上述联盟成员均以对称互惠共生模式而存在的假设，因此，本文进一步假设中介组织和种植企业之间是以产出分享模式（同时成本也按比例共同分担）对劳动收益进行分配，且他们的收益分配比例分别为β、1-β，且0＜β＜1，以及各自成本分摊比例为s、1-s，且0＜s＜1；又设π1，π2分别为中介组织和种植企业的净劳动收益，则有：

在考虑土地流转的产出存在风险的情况下，此时设中介组织和种植企业均为风险厌恶者，风险性成本分别为：

其中，r1和r2分别表示中介组织和种植企业的风险规避程度。

因此，可得到中介组织和种植企业整体及其各自的确定性等价收入为：

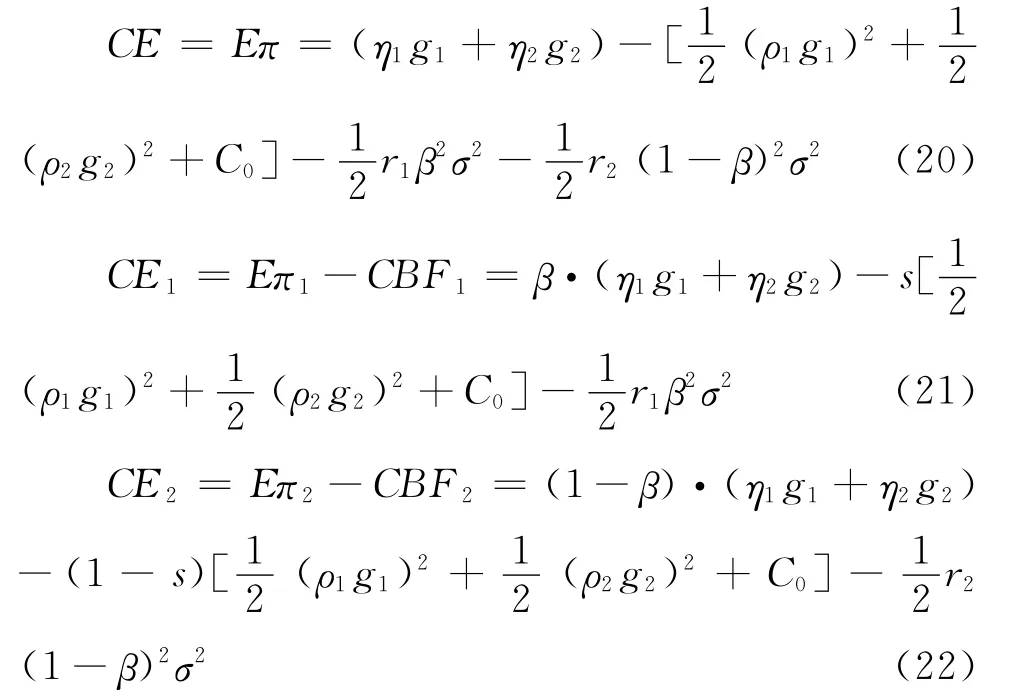
5.1.2 模型的求解

（1）最优努力水平的确定

在对称互惠共生关系中，虚拟厂商是激励契约的设计者，也是该博弈中的领导者，则在此博弈过程中具有“先行一步”的优势，先给出收益分配比例，然后其他利益相关者再根据此选择自己的努力水平。因此，我们首先采用逆推法考虑博弈方的第二步。

假定虚拟厂商给出的收益分配比例已定，分析中介组织和种植企业会怎样选择自己的行动（即努力水平）。根据公式（17）和（18）分别对g1，g2求偏导，且令∂CE1/∂g1=0，∂CE2/∂g2=0，则可得到中介组织和种植企业为追求自身利益最大（即采取不合作行动策略）而在纳什均衡时的努力水平g*1和：

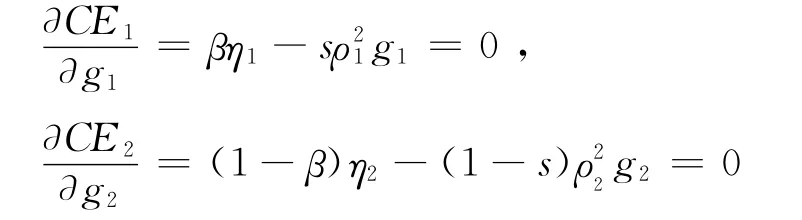
由上述两式可解得：

则有：

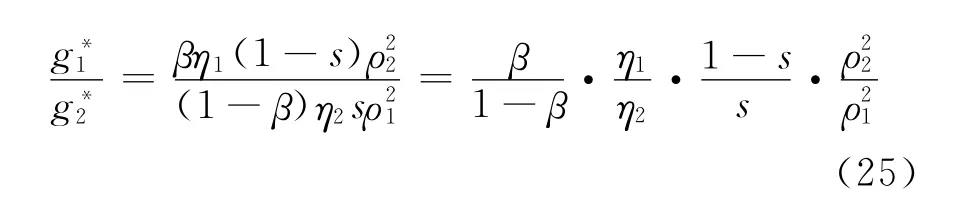
由此，我们可以得出以下结论：

结论1：中介组织和种植企业在追求自身最大效用时所付出的工作努力水平与自身的分配系数成正比，与自身的工作贡献系数成正比，与自身的成本分摊系数成反比，与自身创新性活动的成本系数的平方成反比，而与各自的风险规避程度无关，这与实际情况是完全吻合的，由此可见前面的假设是符合实际的。

（2）最优分配系数的确定

我们再考虑双方博弈的第一步，即最优分配比例的确定。通过式（23）、（24）表明，在满足各自自身效用最大化的情况下，中介组织和种植企业各自根据分配比例来选择最优工作努力水平，反过来，此式亦可表示他们根据各自的工作努力水平来确定最优分配比例β和1-β。因此，将式（23）、（24）带入式（20），然后令∂CE/∂β=0，则可求得：

因此，可以得出如下结论：

结论2：中介组织和种植企业之间分别按照各自成本分摊系数，即s：（1-s）的分配比例分享劳动收益时，可使他们合作的总体净收益达到帕累托最优，因此，β*或1-β*也称为最优分配系数。

那么，再由式（26）和式（27）可得：

因此，又可以得出如下结论：

结论3：在帕累托最优状态时，最优分配系数只与各自承担的成本分摊比例系数有关，且呈正比例关系，说明此时的报酬与付出是完全对等的，而与自身的工作贡献系数、创新性活动的成本系数、项目本身的风险程度及参与人的风险规避程度均无关，这与实际情况是完全吻合的，正所谓“一份耕耘一份收获”，由此可见前面的假设是符合实际的。

（3）实际合作中分配系数的确定

在合作中中介组织和种植企业的实际利益分配系数应根据实际其工作努力水平来调整，此分配原则亦符合我国当前社会主义社会阶段实行“多劳多得，少劳少得”的按劳分配制度，并且依此可加强成员彼此之间的监督与协调，尽量避免共同合作中的“偷懒”或“搭便车”现象［18］。

因此，中介组织和种植企业的收益分配系数可由式（23）和式（24）得到：

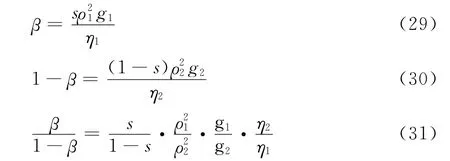
因此，可以得出如下结论

结论4：在实际分配利益时，实际分配系数与各自的工作努力水平、工作贡献系数、创新性活动的成本系数以及各自承担的成本分摊比例系数有关，而与各自的风险规避程度无关，这也是公平合理的。

（4）因劳动要素贡献的分配额

根据对称互惠共生模式的假设，故可忽略风险因素对要素所有者之间造成的影响，即不需对要素贡献分配的结果进行风险系数修正。那么，中介组织与种植企业因劳动要素对总产出贡献额为：

若按照生产要素贡献的原则分配劳动收益时，则中介组织与种植企业因贡献劳动要素而获得的最优收益与实际收益分别为：

5.2 非人力资本要素贡献的分配

相对而言，非人力资本按要素贡献分配较为简单些，正如前文所述非人力资本与其所有者具有可分离性，一旦分离它将不会随着其所有权人的不同而不同，也就是说，无论谁投入非人力资本要素对总产出发挥的作用都是相同的，而且根据对称互惠共生模式的假设，则完全可认为风险与投入成正比关系。因此，非人力资本要素的分配可按投资人投入的要素数量比例进行分配。

5.2.1 因资本要素贡献的分配额

假设中介组织与种植企业的投入资本比例分别为：l与1-l，则中介组织与种植企业因资本要素贡献而获得的收益分别为：

5.2.2 因土地要素贡献的分配额

同理，对于土地要素贡献的分配亦可采取根据投入的土地数量按比例进行分配。但在本文中，只有农户才是土地要素的提供者，则不需要再按比例在成员之间进行分配。因此，农户因土地要素贡献而获得的收益为：

5.3 利益相关者的最优综合分配额

综上所述，农户、中介组织和种植企业因人力资本要素（劳动）和非人力资本要素（土地和资本）贡献而在农村土地间接流转中应获得的最优收益分别为：

6 应用算例

假设：土地流转后的总产出Y0=2000元/亩·年，资本增长、土地增长和劳动增长对土地流转总产出增长的贡献率分别转化为：G′（K0）=25%，G′（L0）=45%，G′（H0）=30%，以及中介组织和种植企业提供资本要素和劳动要素的比例分别为：s：（1-s）=1：4，l：（1-l）=2：3，那么，将上述参数分别代入式（40）、式（41）和式（42）可得到农户、中介组织和种植企业应分配到的收益额为：

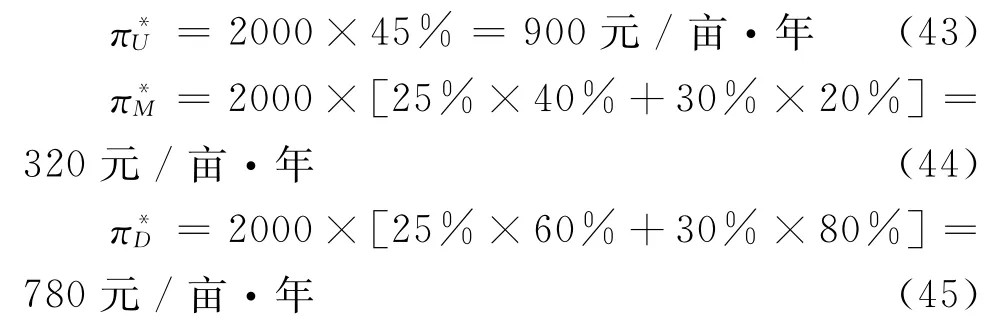
7 结语

从上述可知，本文是在对称互惠共生模式的假设基础上，基于我国当前的“按生产要素贡献参与分配”原则，首先，应用柯布—道格拉斯生产函数理论测度资本、劳动和土地等生产要素的贡献率，从而确定各生产要素对总产出的贡献额；其次，针对劳动者之间因其劳动要素贡献的利益分配问题，鉴于人力资本与非人力资本的特殊性，则采用博弈论的相关理论建立了利益分配模型，从而确定中介组织与种植企业以劳动要素为合作基础的最优利益分配系数，并以此为基础评价合作中他们的实际工作表现，进而确定他们的实际利益分配系数；最后，确定了农户、中介组织和种植企业各自因其贡献而应获得的利益。

［1］杨展.土地流转中的中介组织：非合作博弈框架下的分析［J］.世界经济情况，2006，（2）：30-33.

［2］刘莉君.农村土地流转模式的绩效比较研究［D］.湖南长沙：中南大学，2010.

［3］袁纯清.共生理论及其对小型经济的应用研究［J］.改革，1998，（3）：76-86.

［4］张颖聪，张文秀.农村土地流转市场的委托代理关系分析［J］.农村经济，2005，（4）：31-32.

［5］李怀，高磊.我国农地流转中的多重委托代理结构及其制度失衡解析— —从重庆、四川、广东等省份土地产权流转案例中得到的启示［J］.农业经济问题，2009，（11）：71-77.

［6］许艳.我国农村土地流转中的委托代理问题研究［D］.北京：北京工商大学，2010.

［7］袁纯清.共生理论（第1版）［M］.北京：经济管理出版社，1998.

［8］卓颖，蔡运隆，杨伯伦.基于共生理论的甲烷共气化过程分析［J］.西安交通大学学报，2006，40（3）：324-327.

［9］王朝辉.“资本雇佣劳动”与“劳动雇佣资本”［J］.南开经济研究，2002（2）：52-57.

［10］Thornton P H，Tuma N B.The problem of boundaries in contemeporary research on organizations［J］.Academy of Management Journal，1995：276-280.

［11］赵忠华，王晓华.虚拟企业利益分配要素及其价值确定［J］.商业研究，2002，（24）：4-5.

［12］吴晓霞.马克思的劳动价值论与社会主义收入分配［J］.吉林省经济管理干部学院学报，2002，16（4）：13 -16.

［13］唐焱，吴群.基于C—D生产函数的农用地估价实证研究［J］.南京农业大学学报，2003，26（3）：101-105.

［14］郑玉歆.全要素生产率的测度及经济增长方式的“阶段性”规律——由东亚经济增长方式的争论谈起［J］.经济研究，1999，（5）：55-60.

［15］Hulten C R.Total factor productivity：A short biography［R］.NBER Working Paper，2002.

［16］周其仁.市场里的企业：一个人力资本与非人力资本的特别合约［J］.经济研究，1996，（6）：31-32.

［17］陈菊红，汪应洛，孙林岩.虚拟企业收益分配问题博弈研究［J］.运筹与管理，2002，11（1）：11-16.

［18］卢纪华，潘德惠.基于技术开发项目的虚拟企业利益分配机制研究［J］.中国管理科学，2003，11（5）：60-63.

Research on the Benefit Distribution of the Supply Chain Alliance on Indirect Rural Land Transfer——Based on the Perspective of Symmetrical and Reciprocal Symbiosis

WEN Xiu-chun1，3HE Fang2MA Zhi-qiang3
（1.School of Management，Jiangsu University，Zhenjiang 212013，China；2.School of Economics and Management，Tongji University，Shanghai 201804，China；3.Faculty of Civil Engineering and Mechanics，Jiangsu University，Zhenjiang 212013，China）

As the benefit distribution is a common and critical problem in supply chain alliance，a fair and reasonable plan of benefit distribution is undoubtedly important for supply chain alliance.Based on the perspective of symmetrical and reciprocal symbiosis，according to the benefit distribution principle of production factors contribute，firstly，various production factors（e.g labor，land and capital）contribution rate are determined by Cobb-Douglas production function.Secondly，a game model about human capital factors（e.g labor）is set up and its optimal solution is given，yet the benefit about non-human capital factors（e.g land and capital）is distributed according to their investment proportions.At last，the optimal comprehensive allocations of the farmers，intermediary organizations and plantation companies are respectively obtained by numerical example in land transfer.The analysis in this paper has guiding significances not only for the distribution mechanism of the indirect rural land transfer，but also for the distribution mechanism of cooperation benefits between producers and suppliers.

rural land；indirect transfer；supply chain alliance；benefit distribution；symmetrical and reciprocal symbiosis

F304.8

A

1003-207（2014）07-0052-07

2012-04-10；

2013-06-30

国家自然科学基金资助项目（71073110）；江苏省教育厅高校哲学社会科学基金资助项目（2013SJB6300016）；江苏大学高级人才启动基金资助项目（13JDG041）；江苏省博士后科研资助项目（1302059C）

温修春（1978-），男（汉族），江西赣州人，讲师，管理科学与工程博士后，研究方向：工程管理、房地产投资与土地资源管理等.