闭环供应链中制造商与销售商合作创新模型研究*

徐 伟，郑石桥，陈丹萍

（南京审计学院，江苏南京 211815）

闭环供应链中制造商与销售商合作创新模型研究*

徐 伟，郑石桥，陈丹萍

（南京审计学院，江苏南京 211815）

对废旧产品回收再利用既减少环境污染，又能节约社会有用资源，闭环供应链的研究受到学术界的广泛重视。利用生产函数，在稳定型和风险型市场背景下构造了六类非博弈型创新研究和广告合作的二级闭环供应链模型，并采用多种数学方法给出了模型最优解的存在性与求解方法。信息不对称是供应链的重要特点，提高信息共享程度是未来供应链发展的根本趋势。本文首先根据如下假设进行建模，即创新投入能使再制品单位成本降低，广告投入带来废旧产品回收率提高和再制品销售量的增加；其次，模型求最优解过程中强调合作，提出了应制定内部利润分配规则和联合对外行动决策两套契约的供应链管理思想。各成员放弃（至少是减少）内部“斗智斗勇”，按照保证供应链整体利润最大化的原则确定各方的最佳投资额；最后，对模型进行了仿真分析，应用实例说明了在同样市场背景和创新条件下合作比博弈通常能给供应链带来大得多的利润。另外，无论在稳定型还是风险型市场背景下，平等合作与主从合作供应链总利润相同。因此，主企业要尽量对较弱企业进行扶持，提高供应链整体对外竞争能力。

供应链；合作；创新；投资；逼近

1 引言

无论是从节约资源，减少环境污染的社会效益角度，还是从降低生产成本，增加利润的企业经济效益角度，近年来废旧产品回收再利用受到政府和企业的普遍关注。例如，据统计上海每年废铅蓄电池产生量约8.5万吨，堆起来大约相当于两幢金茂大厦，且这一数量还以每年6000吨的速度递增。除了公布上海每年废铅蓄电池产生量外，最近召开的相关研讨会还透露，上海合法收集的电瓶数量不足10%，因非法处置而倾倒的含铅废硫酸液每年大约在7000吨。2010年4月，国家发改委确定了14家汽车零部件再制造试点企业和35家机电产品再制造试点企业，仅汽车零部件再制造试点工作，中央财政就已经投入了8000万元，发展再制造业每年可节约1550亿元，可获得巨大环境效益［1］。不少企业把逆向物流回收利用的研究纳入战略规划。闭环供应链的研究引起了很多学者的兴趣，熊中楷等［2］研究了经销商附带从事回收品再制造，与新产品生产进行竞争的闭环供应链。达利庆等［3］讨论了逆向物流系统结构研究现状并提出了进一步研究的方向。Savaskan，Bhattacharya和Van Wassenhove［4-6］在研究回收渠道选择时，均假设旧产品回收数量上受到上期销售新件的限制。Ferrer和Swaminathan［7］探讨了独立制造商和原始设备制造商的竞争。Guide Lr和Van Wassenhove［8］研究了如何通过供需匹配实现再制造的利润最大化。Heese，Cattani和Ferrer［9］将闭环供应链的研究拓展到寡头垄断的环境，探讨了双寡头垄断市场中，废旧产品的回收对寡头竞争优势的影响。Bakal和Akcali［10］探讨了多周期随机需求下的回收定价策略。徐家旺等［11］对闭环供应链管理中逆向物流回收与重新利用、闭环供应链结构设计、运作、契约协调和不确定性等问题的研究现状进行了综述，并给出了若干研究结果。曹俊［11］等研究了新产品与再制造产品价格，质量均存在差异情况下，新产品与再制造产品定价策略与协调问题。王文宾等［12］进一步研究了以制造商为主导，销售商为主导，以及制造商和销售商基本平等三种渠道权力情况下，新产品与再制造产品定价策略与协调问题。

成员间信息不对称是供应链的一个重要特点，提高信息共享程度是供应链管理研究的一个重要课题，叶飞，徐学军［13］对供应链伙伴特性、伙伴关系与信息共享的关系进行了研究。曹柬等［14］研究了不对称信息下供应链利润分成制契约。但目前这类研究都是在信息共享程度不高条件下，假设供应链上、下游企业间存在不同程度的对抗，讨论的基本上都是合作-博弈模型。其中还有一些讨论完全不合作的双寡头对抗模型。各项决策指标的大小，各成员企业都只从自身利润最大化出发，而不是从整体利润最大化来决定。纵观供应链成员合作伙伴关系发展的历史，随着竞争的加剧和市场环境的变化，人们意识到只有加强合作，结束对抗，方能应对快速多变的市场。这迫使企业从传统的对立关系朝着一个真正基于合作、互惠互利、信任和关系交换的合作伙伴关系方向发展［15］。尤其是在当今的知识经济时代，往日的卖方市场基本上由买方市场所取代，寡头垄断市场的情况几乎不再可能，单个企业间的竞争向供应链间竞争转化，供应链成员企业内部应加强合作，一致对外已成必然趋势。另外，每条供应链的业务在整个市场中也都只占有很小的份额，形成不了垄断。供应链之间的竞争也日益趋于理性化。人们开始注意到，供应链的存在与发展更重要的是要创造新的价值，供应链成员的创新性合作既是创造新价值的最根本途径，也是产生和维持供应链竞争优势的最为可行的战略［16］。

我们认为，过去的供应链管理只是制定单一的契约，既是供应链整体利润在各成员企业间再分配方案，也是供应链各成员企业对外的行动规则。但是，各成员往往把主要精力放在内斗上。今后供应链管理将转化为制定内、外部两套契约。制定内部契约主要应体现奖惩分明，充分调动全体成员企业的积极性，保持供应链的稳定，一般应遵循：

利益分配基本原则：（1）互利互惠原则。基本思想是要各成员企业从供应链中获得的利益不小于不参加供应链所获得的利益。（2）按照贡献分配原则。这里的贡献包括投入的资金、设备、人力、管理等总资源。（3）风险补偿原则。各成员企业从供应链中获得的利益与其承担的风险应对等。

外部契约，即供应链成员企业以大局利益为重，全面合作，求同存异，一致对外，争取供应链整体获得最大利润的行动决策。以下我们只讨论外部契约。

本文考虑由一个制造商和一个销售商组成的二级闭环供应链，为了论述简单起见，考虑供应链只经营一种商品。其中制造商既生产新产品，也生产再制造品，销售商同时负责回收旧产品。

假设1 一件正常的回收品其零部件只用于生产一件再制造品，制造商原来总产品中再制造品占的比重为r0，即原来产品的回收率为r0.原来新制品单位变动成本为c0，再制造品单位加工变动成本为c1，旧产品回收价格为p*，满足p*+c1＜c0.制造商和销售商共同固定成本为C*，新制品和再制造品质量相同，销售价格都是p0.再制品变动成本有比较大的压缩空间。

现在制造商拟投入一笔创新研究经费x，希望通过研究一方面提高再制品中利用回收零部件的比例；另一方面改进利用废旧零部件进行再制造的工艺技术，整体上降低再制品的成本。另外，尽可能高的旧产品回收率显然也是影响闭环供应链效益的一个重要因素。销售商拟投入一笔广告费用y，用于宣传产品质量、回收旧产品和以旧换新的重大意义（减少污染以及给消费者带来实惠）。

本文对社会环境、商品的市场需求、供应链生产状况作下列基本假设。

假设2 商品的零部件能反复回收和再制造，且回收的零部件经过加工与新制的零部件质量能达到无差异水平。为了让消费者对购买的商品质量不产生疑惑，新产品和再制造品质量也确实没有差异，销售价格也相同，都是p0.旧产品回收的价格p*是合理的，即对回收品按质定价公平，不存在对顾客欺诈。供应链生产的商品创新前总销售量是Q0。

假设3 从C-D生产函数角度，制造商拟投入的科研（包括设备改进）费用x，使每件再制造品制造成本减少fxα，其中f＞0，0＜α＜1［17］。销售商拟投入的广告费用y，能使旧产品回收（包括以旧换新）率增加gyβ.且由于广告宣传作用，顾客觉得旧产品回收或直接以旧换新方便，使得该种商品销售量增加到Q=Q0+hyγ.其中h＞0，0＜g＜1，0＜β＜γ＜1，αγ＜（1-α）（1-β）［12］。另外，我们还假设g，β的值都很小，对充分大的y都能保持r0+gyβ＜1。

2 相对稳定的市场模型

任何投资都是有一定风险的。但是，如果市场环境基本平稳，投资收益比较确定，认为投资风险不大，几乎可以忽略。我们称这种环境下的市场是相对稳定的。供应链中各成员企业对投资都充满信心，分析的目的主要是为了较精确地测定所需要的投资额。本节设f，g，h都是常数。

2.1 平等合作，投资各自独立承担模型

设制造商与销售商地位基本平等，没有某一方占绝对优势，它们根据各自掌握的经济方面、科技方面、需求方面等信息优势，计划要达到的发展目标，抱着真诚合作的态度，本着风险与利润对等分摊的原则，商讨自己拟投资于研发费或广告费资金数量（即投资策略），使得供应链可能达到最大均衡销售量，也使自己可能得到较大利润。同时由于研发和广告费用，生产成本等预先都不可能完全准确测定，以及信息不可能完全共享，各成员企业间尽管有内部纷争，但能合作一致对外。

创新后商品回收率为：创新后再制品单位变动成本为：

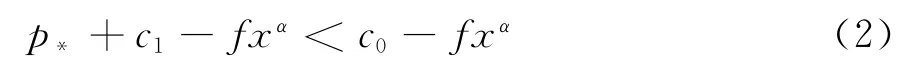
供应链创新研究与广告投入后的总利润为：

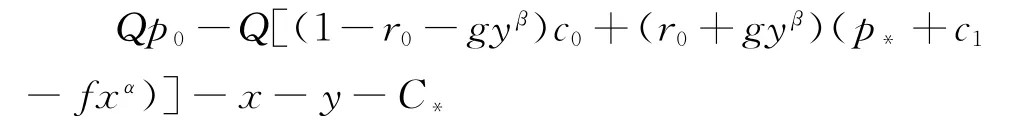
供应链创新研究与广告投入后比创新前多得到的总利润为：

因此，我们的模型就是下面的无约束规划问题

令（4）分别对x，y的偏导数为零，并化简得到：

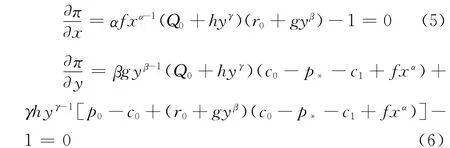
由（5）解得：

把（7）带入（6），并化简得到：

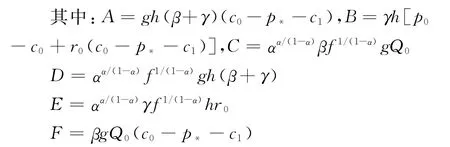
都是正的常数。我们断定方程（8）至少有一个正解y*，从而由（7）有对应的正数x*，使（x*，y*）作为规划问题（4）的最优解。事实上，作关于变量y的连续函数

命题1 在假设1，2，3成立条件下，根据利益分配基本原则，无约束规划问题（4）至少有一组最优投资（x*，y*）方案。

2.2 主从合作，投资不平均承担模型

设供应链上、下游企业地位不平等，某一方占绝对优势。例如制造商是一家实力十分强大的生产型企业，在供应链中起主导作用，而销售商与制造商的关系有两种情况：（i）销售商主动要求加入制造商主导的供应链联盟，愿意努力按照制造商规定的价格推销产品和回收旧产品，并承诺为制造商承担部分研究费用。（ii）制造商邀请销售商加入自己主导的供应链联盟，并希望销售商能按照自己确定的价格推销产品和回收旧产品，为了减轻销售商对投资风险的顾虑，承诺为销售商承担部分广告费用。但也可能销售商是一家名气很大，信誉很高的大型企业，在供应链中起主导作用，而制造商与销售商的关系也有两种情况：（iii）制造商主动要求加入销售商主导的供应链联盟，愿意努力为销售商及时提供质优价格合理的产品，并希望销售商能与自己商定销售产品和回收旧产品的价格，承诺为销售商承担一定比例的广告费。（iv）销售商邀请制造商加入自己主导的供应链联盟，并希望制造商能与自己商定销售产品和回收旧产品的价格，为了减轻制造商对投资风险的顾虑，并承诺为制造商承担部分研究费用。本文中只讨论其中的情形（i），其它3种情形类似分析。另外增加以下假设。

假设4 销售商允诺：为了支持制造商开展的科研行动，愿为制造商承担比例为t的创新研究费，但希望制造商在内部分配供应链总利润时有所体现。

同样用x，y分别表示制造商直接投入再制造品创新研发，销售商独立投入回收旧产品广告宣传的费用额。则实际用于投入再制造品创新研发和投入回收旧产品广告宣传的费用分别为：

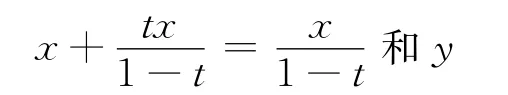
由模型（4）的求解过程容易得到：

命题2 在假设1，2，3，4成立条件下，根据利益分配基本原则，无约束规划问题（9）至少有一组最优投资方案。其中（x*，y*）正好是命题1中给出的结果。另外制造商和销售商分别承当的投资费用为x*和y*+。

2.3 主从合作，主企业独自承担投资模型

设制造商是供应链的主导，并独立决策，独自承担全部投资风险。制造商有两个决策变量：再制品创新研究费用x和旧产品回收价格p。

假设5 经过测算旧产品回最高收价格为p*，即p*≤p≤p*，且存在两个正的常数k1，k2，旧产品回收率为r0+k1（p-p*），但r0+k1（p*-p*）＜1；同时由于旧产品回收价格增大，刺激该种商品销售量增加k2（p-p*），代替假设3中广告费y带来的销售量增大kgyβ，使得Q=Q0+k2（p-p*）。

创新后商品回收率为：）

供应链创新研究与广告投入后的总利润为：

供应链创新研究与广告投入后比创新前多出的总利润为：

因此，我们的模型就是下面的约束规划问题：

令式（12）对x的偏导数为零，并化简得到：

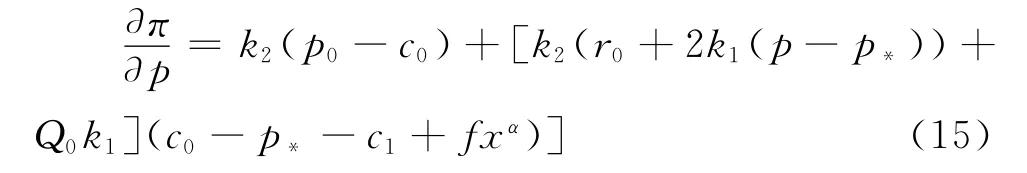
易见式（14）右边恒大于零，说明总利润π关于p严格递增。

于是当p=p*，对应的x*=［αf（r0+k1（p*-p*））（Q0+k2（p*-p*））］1/（1-α）时，π达到最大值。

命题3 在假设1，2，3，5成立条件下，约束规划问题（12）有唯一最优解（x*，p*）。

解得：

再计算式（12）对p的偏导数，得到

3 风险型市场模型

如果市场环境不是很平稳，投资收益波动较大，投资风险不可忽略，供应链各成员企业对投资都十分谨慎。本节考虑假设3中的f，g都是随机变量。

假设6 f，g，h分别是区间0＜a1＜b1，0＜a2＜b2＜1，0＜a3＜b3上的随机变量。且f，g独立，有关数学期望和方差分别为：

3.1 平等合作，各方独立承担投资风险模型

考虑假设1，2，3，6成立，由于f，g，h都是随机变量，规划模型（4）在这里变成随机规划模型。并按照随机规划的通常解法［18］，将模型中的随机数用其数学期望代替，使随机规划转化为普通规划（注：独立随机变量乘积的数学期望等于数学期望的乘积）。

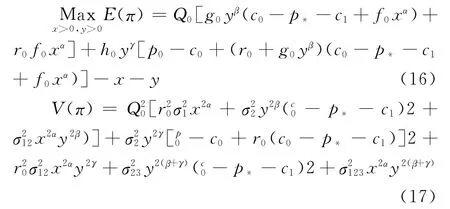
令（16）分别对x，y的偏导数为零，并化简得到：

由式（18）解得：

将式（20）代人式（19），并化简得到：

其中：都是正的常数。类似于方程组（7），（8）的讨论，我们断定方程组（20），（21）至少有一个正解，作为规划问题（16）的最优解。利用数值逼近的方法可得方程组（20），（21）精确到任意程度的解（x*，y*）.

命题4 在假设1，2，3，6成立条件下，约束随机规划问题（16）至少有一组最优解（x*，y*）。但最大利润具有由方差（17）表示的风险。

3.2 主从合作，投资不平均承担的风险模型

考虑假设1，2，3，4，6成立，对应于无约束规划模型（9），我们有无约束随机规划模型：

利用2.2节和3.1节中的讨论，我们有：

命题5 在假设1，2，3，6成立条件下，无约束随机规划问题（22）至少有一组最优解方案。其中其中（x*，y*）正好是命题4中给出的结果。制造商和销售商分别承当的投资费用为x*和但最大利润具有由方差（23）表示的风险。

3.3 主从合作，主企业独自承担投资风险的模型

考虑假设1，2，3，5，6成立，并对假设5，6中的f，k1，k2补充规定：k1，k2也都是随机变量，f，k1，k2彼此独立，且承载概率密度函数E（k1）==-p*）＜1， V（k1）=，V（k1k2）== ρ2

123。

对应于约束规划模型（12），我们有约束随机规划模型：

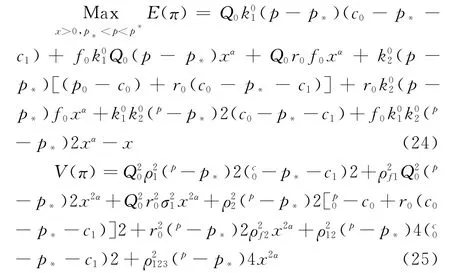
令式（24）关于x的偏导数为零，得到：

而式（24）关于p的偏导数为：

命题6 在假设1，2，3，5，6及假设5，6补充规定成立条件下，约束随机规划问题（24）有唯一组最优解（x*，p*）.但最大利润具有由方差（25）表示的风险。其中x*为p=p*式（26）的值。

4 仿真分析

设某种大型品牌空调，制造商既生产全新产品，也利用回收的本牌号旧产品生产再制造品，再制造品与全新产品质量完全没有区别。由一家大型全国连锁的超市负责销售，并负责直接回收旧（或以旧换新）本牌号空调，销售价格p0=15000元，每年销售量约Q0=20万台，旧空调回收价p*=1500元。全新产品单位变动成本c0=10000元，再制造品单位变动成本c1=7000元，制造商与供应商共同固定成本仍记为C*，旧产品回收率r0=0.2.现在制造商与销售商拟合作进行投资，就旧产品回收率和回收品零部件利用率方面做一些工作，争取供应链获得尽可能大的新利润。为了压缩篇幅，只对3.1节，3.3节两个风险模型作仿真。设有关参数为：E（f）=50，E（g）=0.05，E（h）=50，α=0.2，β=0.1，γ=0.3，V（f）=V（h）=3，V（g）=0.001，V（fg）=V（gh）=0.1，V（fh）=V（fgh）=5.E（k1）= 0.0004，E（k2）=4，V（k1）=0.00001，V（k2）= 0.4，V（k1k2）=0.0001，V（fk1k2）=V（fk1）= 0.001，V（fk2）=5，p*=2500元。

（1）按平等合作，各方独立承担投资风险模型

首先把有关参数值代入方程组（20），（21），得到

x=17.7828［（0.2+0.05y0.1）（200000+ 50y0.3）］0.25

y0.9-1500y03-78750y0.2-（17782.7+ 17.7827y0.3+53.3485y0.2）·［（0.2+0.05y0.1）（200000+50y0.3）］0.25-1500000=0

利用数值逼近的方法得到最优投资为x*= 3.11494×107元，y*=2.4781500×107元。有希望带来再制品单位变动成本降低1506元，旧产品回收率增加0.2744，每年产品销售量增加8264台。

再利用式（16）计算，得到供应链创新投入后比创新前多出的期望总利润E（π）=2.22383×108元。用式（17）算得，获利的风险V（π）=1.17993× 1014元。

（2）主从合作，主企业独自承担投资风险的模型

首先把有关参数值代入式（26），得到制造商独自投资科研费x*=4.07124×107元，确定今后旧产品回收价格p*=2500元。有希望带来再制品单位变动成本降低1663元，旧产品回收率增加0.4，每年产品销售量增加4000台。

再利用式（24）计算，得到供应链创新投入后比创新前多出的期望总利润E（π）=2.98513×109元。利用式（25）算得，获利的风险V（π）=1.12805 ×1019元。

5 结语

创新与合作是供应链未来发展的两大方向。创新使供应链不断获得新的生命气息，合作是供应链对外竞争的强大武器。大多数学者比较注重供应链成员企业间的博弈与竞争，其实供应链成员间更需要的是合作，供应链管理应制定内部利润分配规则和联合对外的行动决策两套契约。一般说来，无论是在相对稳定市场条件下，还是在风险型市场条件下，合作型供应链比博弈型供应链信息共享程度高，且供应链成员间互信程度也高，所以合作型供应链比博弈型供应链整体利润通常要大得多。另外，由于平等合作与主从合作的供应链总利润通常是一样的，所以强强合作的供应链一般自然采取平等合作方式，但对非强强合作的供应链中，主企业要积极鼓励和扶持较弱的企业进行创新。

附录:命题1的证明

创新合作后，供应链总产品Q中新制品和再制品分别占的比重为1-r0-gyβ和r0+gyβ，平均单位成本为（1-r0-gyβ）c0+（r0+gyβ）（p*+c1-fxα）.因此创新研究与广告投入后的总利润为：

其中Q=Q0+hyγ。另外，创新合作前供应链平均单位成本为（1-r0）c0+r0（p*+c1），总利润为：

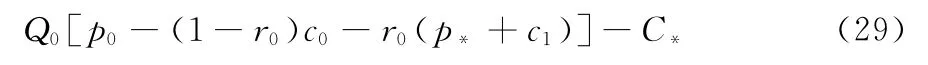
式（28）减式（29）即得供应链创新研究与广告投入后比创新前多得到的总利润，由式（6）表示。

把（6）两边同乘以y1-β并重新排列得到：

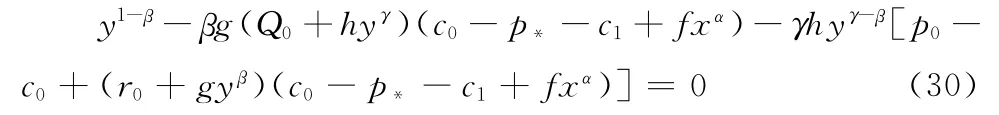
把（7）代入（30）并整理得：

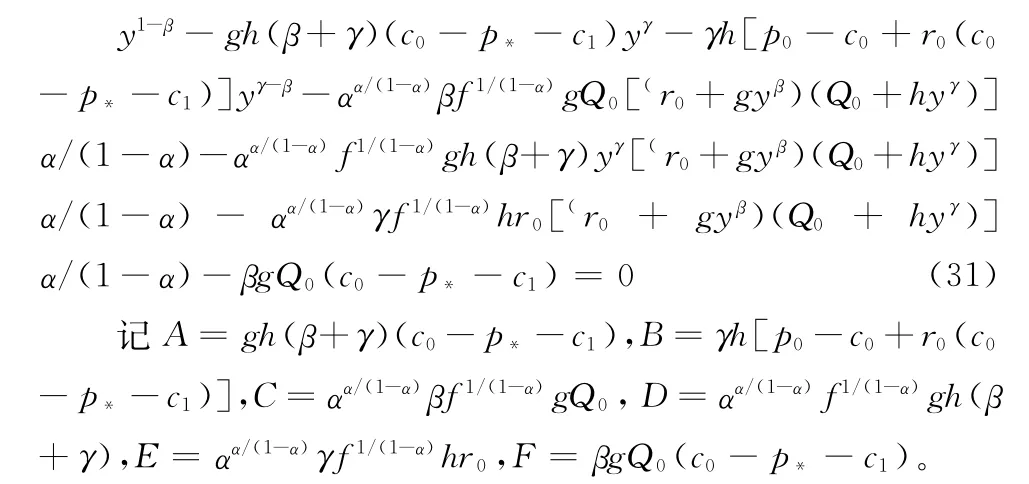
从而（31）的左边可写为：

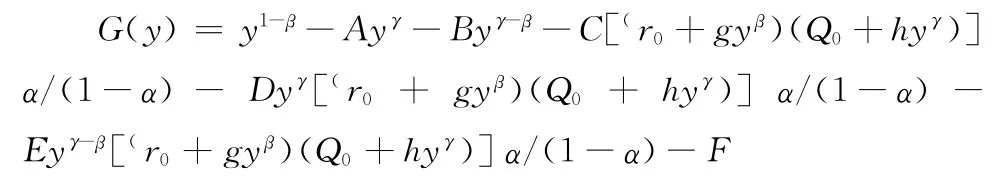
［1］潘少军.再制造业每年可节约1550亿元，获巨大环境效益［MOL］.中国证券网（2010-08-26）.www. cnstock.com/index/gdbb/201008/805535.htm.

［2］熊中楷，王凯，熊榆.经销商从事再制造的闭环供应链模式研究［J］.管理科学学报，2011，14（11）：1-9.

［3］达庆利，黄祖庆，张钦.拟向物流系统结构研究的现状及展望［J］.中国管理科学，2004，12（1）：131-138.

［4］Savaskan R C，Bhattacharya S，Van Wassenhove L N. Channel choice and coordination in a remanufacturing environment［R］.INSEAD，Working Paper，2000.

［5］Savaskan R C，Bhattacharya W，Van Wassenhove L N. Ciosed-loop supply chain modrls with product remanufacturing［J］.Naagement Science，2004，5（2）：239-252.

［6］Savaskan R C，Van Wassenhove L N.Reverse channel design：The case of competing retailers［J］.Management Science，2006，52（1）：1-14.

［7］Ferrer G，Swaminathan J M.Managing new and remanufactured products［J］.Management Science，2006，52（1）：15-26.

［8］Guide Lr V D R，Teunter R H，Van Wassenhove L N. Matching demand and supply to maximize profits from remanufacturing［J］.Manufacturing&Service Operations Management，2003，5（24）：303-316.

［9］Heese H S，Cattani S K，Ferrer G，et al.Competitive advantage through take-back of used products［J］.European Journal of Operational Research，2005，164（1）：143-157.

［10］Bakal I，Akcali E.Effects of random yield in revese supply chains with price-sensitive supply and demand［J］.Production&Operations Management，2006，15（3）：407-420.

［11］徐家旺，朱云龙，黄小原，等.闭环供应链管理问题的研究进展［J］.系统工程，2008，26（8）：1-11.

［12］王文宾，达庆利，聂锐.考虑渠道结构的闭环供应链定价与协调［J］.中国管理科学，2011，19（5）：29-36.

［13］叶飞，徐学军.供应链伙伴特性、伙伴关系与信息共享的关系研究［J］.管理科学学报，2009，12（4）：115-128.

［14］曹柬，杨春节，李平，等.不对称信息下供应链线性分成制契约设计研究［J］.管理科学学报，2009，12（2）：19 -30.

［15］高本河，繆立新，沐潮.供应链管理［M］.深圳：海天出版社，2004.

［16］Patterson K A，Grimm C M，Corsi T M.Adopting new technologies for supply chain management［J］. Transportation Research Part E，2003，39（2）：95-121.

［17］Cohen W M，Klepper S.Firm size and the nature of innovation within industries：The case of process and product R&D［J］.The Review of Economics and Statistics，1996，78（2）：232-243.

［18］王金德，随机规划［M］，南京：南京大学出版社，1990.

Study on Collaboration and Innovation Model of Manufacturers &Sellers in the Closed-loop Supply Chain

XU Wei，ZHENG Shi-qiao，CHEN Dan-ping
（Nanjing Audit University，Nanjing 211815，China）

Because recycling the EOL products can both diminish environmental pollution and save useful social resources，widespread importance is attached to research of closed-loop supply chain by the academia.Six types of non-game closed-loop supply chain models of two levels are built based on innovation study and cooperation by the production function against backgrounds of stable and risk market and the ex-istence of the optimal solution of the models and and the corresponding approaches is proved by using multi-mathematics methods.Information asymmetry is an important characteristic of supply chain and an increase in the share of imformation is a fundamental trend of supply chain development in times to come. Firstly，according to the following assumptions：innovation input can decrease the unit cost of remake and advertisements input，models proposed in this paper can increase the recyleing rate of EOL products and sales volume of remake.Secondly，collaboration is stressed in the course of finding the optimal solution of the models and supply chain management idea of making two sets of rules is put forward，for internal profit distribution and allied decision-making.Each member should abjure（or diminish at least）the internal fight.The amount of investment by each member is determined by the principle of ensuring the maximal profit of the whole supply chain.Finally，an emulational analysis of the model is made and by case study show that cooperation often brings much more profit to the supply chain than game in the same market and under the same innovation condition.Besides，the total profit of equal cooperation and subordinative cooperation remains the same wether under stable or risk-market conditions.Thus，host enterprises should try their best to support weaker enterprises to increase competitiveness of the whole supply chain.

supply chain；cooperation；innovation；investment；approximation

F252

A

1003-207（2014）07-0116-08

2012-10-07；

2013-11-29

国家社科基金资助项目（13AZD002）；教育部人文社会科学基金资助项目（14YJA630041）；江苏省教育厅高校哲学社会科学基金资助项目（2014SJB192）

徐伟（1977-），男（汉族），安徽马鞍山人，南京审计学院国际商学院讲师，研究方向：经济管理、会计与审计.