运筹学在燃气行业的应用

朱凯敏 霍小亮

(1.中国市政工程西南设计研究总院有限公司，四川成都 610081;2.晋能燃气集团有限公司，山西太原 030002)

运筹学(Operations Research)是一门管理有组织系统的科学，它通过建立数学模型，运用规划论、存储论、排队论、图论与网络分析等数学方法，对作业合理安排，以达到经济有效地利用资源［1］。运筹学研究的系统难以采用试验的方法，而必须依赖数学模型。燃气行业中诸如生产物资调运，运营线路选择，输配系统优化［3］、最大输气能力分析及最短敷管路由等问题也难以搬进实验室，常不得已而采用经验或保守决策，造成管理的粗放和资源的浪费。本文将以气源调度最低运行成本、巡线最短重复路径、输配系统最大流三个具体问题，介绍运筹学方法在燃气行业的应用。

1 物资调配运输

物资调运成本取决于供应方、运输方式、运距和运输成本等因素。如制管厂向不同分厂的任务分配和钢板厂的钢板供应，又如管道工程中钢管与防腐管的调运等［4］，再如燃气管网的气源调度。这些物资调运问题均能通过建立线性规划模型，寻求最优调运组合方式，并通过“敏感性报告”分析变量对最优组合的影响。

问题:某市的三个区Bj(j=1，2，3)年需天然气320个单位、250个单位和350个单位，由已签订照付不议协议的Ai(i=1，2)两门站供应，其最大年供应量分别为400个和450个单位，Ai门站供应Bj区的单位成本详见表1。由于供不应求，决定B1发展0个～30个单位用气量的可中断用户，保证B2，B3供应量不低于270个单位，求供应无过剩时输送成本最低的气源调度方案。

表1 天然气供需量和单位天然气的输送成本

解:设Xij为Ai门站输往Bj的气量，则最低输送成本的目标函数:MinZ=15×X11+18×X12+22×X13+21×X21+25×X22+16×X23;

需满足的约束条件:1)输往B1的约束条件:290≤X11+X21≤320;2)输往B2的约束条件:X12+X22=250;3)输往B3的约束条件:270≤X13+X23≤350;4)门站 A1供应量的约束条件:X11+X12+X13≤400;5)门站 A2供应量的约束条件:X21+X22+X23≤450;6)供应无过剩的约束条件:X11+X12+X13+X21+X22+X23≥850。借助Excel的“规划求解”工具可求得最低输送费用为14 650，Xij值详见表2。燃气的物资调运问题还可运用运筹学的“表上作业法”(如最小元素法、西北角法)求解，因其步骤晦涩难懂，这里不再赘述，读者可参阅文献［1］［2］学习。

2 中国邮路问题

“中国邮路问题”指邮差从邮局出发并走遍所负责的街道去送信后返回邮局，如何可使重复的路径最短。燃气巡线、用户安检与抄表、瓶装气供应站的气罐配送等均可转化为中国邮路问题，并借图论与网络分析的“奇偶点图上作业法”选取最短重复路径。

问题:巡线工从输配所m出发，巡检图1(其上数字为道路长度)的13条道路上的燃气管线后，返回m。自然地，若要完成巡线任务，则至少应走过每条街道一次，问何种走法总行程最短。

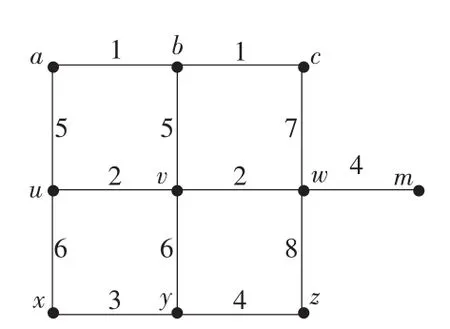
图1 巡线路网图

求解该问题前先认识图论与网络分析的几个概念和寻优的思路。奇点:图G中，以V为端点的边数为奇数条时，则V点为奇点;初等圈:图G中，某个圈既无重复点也无重复边者为初等圈;欧拉图:若存在一条回路，经过每边一次且仅一次，则称该回路为欧拉回路;具有欧拉回路的图称为欧拉图，图G是欧拉图的充要条件是图G中无奇点。

实际路网形成的图G中存在T字路口、断头路等奇点，因此存在重复行走的路段。“奇偶点图上作业法”寻最短重复路径的原理是在两两奇点之间构造重复边以消除奇点，从而将图G转化为欧拉图，新增的重复边就表示重复走过的路段。当构造的重复边满足以下条件时，重复的路径最短:条件A，每条边最多重复一次;条件B，图G中每个初等圈，重复边的长度不超过圈长的一半。

解:第1步:定初始可行方案。

图1存在b，u，y，m四奇点，因此不是欧拉图。将b与y配对作b-c-w-v-y重复边，u与m配对作u-v-w-m重复边，所构造的欧拉图如图2a)所示，其含重复边在内的任一欧拉回路均为可行方案，但非最短重复路径，此时重复边的总长为:Lbc+Lcw+Luv+2Lvw+Lwm+Lvy=24。

第2步:调整可行方案，使重复边最多为一次以满足“条件A”。去除(v，w)重复两次的边，调整为图2b)，重复边的总长降为:Lbc+Lcw+Luv+Lwm+Lvy=20。

第3步:逐个检查初等圈，使其满足“条件B”。

初等圈“b-c-w-v-b”中，圈总长为15，而重复边的总长为8，大于该圈总长度的一半，作重复边(b，v)，(v，w)代替(b，c)，(c，w)，调整为图2c)，重复边总长降为:Lbv+Lvw+Luv+Lwm+Lvy=19。同理，对初等圈“u-v-b-a-u”调整为图2d)，此时所有初等圈均满足“条件B”，重复边总长为 Lab+Lvw+Lau+Lwm+Lvy=18。“m-w-vw-c-b-a-b-v-u-a-u-x-y-v-y-z-w-m”或“m-w-z-y-v-w-c-b-v-u-a-b-a-u-xy-v-w-m”等任一欧拉回路均为最短重复路径。

图2“奇偶点图上作业法”寻优过程

3 管网最大流问题

问题:图3为以vs为起点的某中压输气管网，已知管道扣除途泄流量后的转输流量和流向如图3数字和箭头所示，现探讨该管网经终点vt向相邻中压管网的应急供气能力，即最大转输量。

图3 中压输气管网简图

图4 初始可行流

上述管网的流量满足以下三个条件，则是可行流:1)每条边(vi，vj)的流量fij不超过各自的容量cij;2)源点输出的量等于汇点输入的量;3)中间点流入流出平衡。

定义μ为图G中方向从vs到vt的一条链，μ上的边与μ同向则称为前向边，反向则为后向边，其集合分别用μ+和μ-表示，可行流f如满足，则称μ为从vs到vt的(关于f)的可增广链。可增广链意味着沿该链从vs输送到vt的流f未饱和。故求最大流的方法为:寻找并调整可行流的可增广链，每次调整之后的流量f'均比原来的可行流f要大，重复几次直到不存在关于该流的可增广链时就得到了最大流。

图5“标号算法”求解过程

下面介绍用“标号算法”求取管网最大流的方法，标号过程中每条边上的有序数表示(cij，fij)。

第1步:标号过程，用以寻找可增广链。

1)给发点 vs标号(Δ，+∞);

2)选择一个已标号的点vi，对于vi所有未标号的邻接点vj用以下方式标号:a.若边(vi，vj)为后向边，且 fij＞0，则令 δj=min(fij，δi)，并给 vj以标号(-vi，δj);b.若边(vi，vj)为前向边，且 fij＜cij，则令 δj=min(cij-fij，δi)，并给 vj以标号(+vi，δj)。

3)重复步骤2)直到收点vt被标号或不再有顶点可标号时为止。若vt得到标号，说明找到一条可增广链，转第2步调整过程;若vt未得到标号，标号过程已无法进行时，说明f已是最大流。

第2步:调整过程，用以沿可增广链调整f以增加流量。

2)去掉所有标号，回到第1步，对可行流f'重新标号。

解:1)因总存在可行流(如0流)，定义一个如图4所示的初始可行流，其转输能力为6;2)按标号算法的第1步进行第一次标号，结果如图5a)所示，由于vt被标号，说明存在可增广链，由标号从后往前找到可增广链为“vs-v1-v4-vt”;3)按标号算法的第2步对可增广链“vs-v1-v4-vt”进行第一次调整后，其转输能力增至7，结果如图5b)所示;4)按标号算法的第1步进行第2次标号，找到可增广链为“vs-v3-v4-vt”，结果如图5c)所示;5)按标号算法的第2步对可增广链“vs-v3-v4-vt”进行第二次调整后，其转输能力增至9，结果如图5d)所示。此时f4t，f5t均已达到各自容量 c4t，c5t，进行第3次标号时vt不可能获得标号，说明已不存在可增广链，因此管网的最大转输能力为9。

4 结语

随着精益管理要求的提出以及越来越多的燃气管理和运营人员参与运筹学等管理学科的学习，相信运筹学的方法和理念将会逐步融入到燃气工程建设和运营管理中来，为企业提供更科学的决策依据。

［1］胡运权，郭耀煌.运筹学教程［M］.第3版.北京：清华大学出版社，2007.

［2］蓝伯雄.管理数学(下)——运筹学［M］.北京：清华大学出版社，2003.

［3］李书波，仙立东.运筹学在燃气输配系统中的应用［J］.系统工程理论与实践，1997(6)：135-138.

［4］田进波，李雪松，邢俊强.运筹学在管道物流管理中的应用［J］.石油工程建设，2010(36)：153-154.

［5］陈御钗，王建洲.运筹学在化工企业中的应用［J］.广东化工，2007，34(10)：128-131.