基于裂纹形核理论的橡胶制品疲劳研究*

李志超，危银涛，金状兵，王 昊，何 园,4

(1.湖南工业大学 机械工程学院，湖南 株洲 412007;2.清华大学 汽车安全与节能国家重点实验室，北京 100084;3.湘潭大学 土木工程与力学学院，湖南 湘潭 411105;4.西安交通大学 航天航空学院，陕西 西安 710049)

橡胶制品的疲劳寿命评估一直是橡胶产品设计棘手的难题，目前工程上广泛应用的方法是疲劳寿命S-N曲线法[1-2]和基于断裂力学的疲劳裂纹扩展方法[3-7]。S-N曲线法是一种基于物理实验了解材料疲劳特性的方法，该方法能有效预测橡胶产品的疲劳寿命，但需要建立庞大的疲劳实验数据库，实验非常耗时耗资，且只能在产品开发的后期进行，产品疲劳设计风险系数颇高。因此，国内外学者均试图从理论上对橡胶材料的疲劳评估提供保证。近年来针对橡胶制品处于多轴复杂周期载荷作用的疲劳估算方法出现了许多新的分析模型，但由于橡胶的大变形引发的应力应变复杂性，加之结构形状、环境甚至材料的分散性等众多因素的影响,尚未形成统一的橡胶材料疲劳估算理论。目前使用比较广泛的疲劳估算理论主要有等效应变法、能量法、等效应力法以及临界面法[8-12]。

基于开裂能理论的橡胶疲劳分析方法是MARS[13]于2001年提出的一种新的橡胶疲劳分析与预测理论，该理论能够解析橡胶的多轴疲劳规律，有效结合断裂力学方法和S-N的曲线方法的优点，减少了疲劳表征的难度和工作量，且具有临界面的特征，可同时预测疲劳寿命和裂纹萌生方向，为快速进行橡胶构件的疲劳设计和评估提供了一种有效的途径。

本文基于开裂能理论，对嚢式空气弹簧的橡胶支座进行疲劳寿命评估与改进，分析结果与实验结果吻合良好，表明了该方法对橡胶构件疲劳寿命分析的有效性。

1 基于开裂能理论的橡胶制品疲劳分析基本流程

基于开裂能理论的橡胶制品疲劳分析基本流程为：材料参数的获取、有限元仿真、开裂能和疲劳寿命的计算。

1.1 橡胶材料参数获取

进行橡胶制品疲劳分析所需要的材料参数包括橡胶超弹性本构模型参数和橡胶材料疲劳特性参数，其中超弹性本构参数用于有限元仿真，材料疲劳参数用于寿命计算。超弹性本构模型参数是通过单轴拉伸、平面拉伸和等双轴拉伸实验获得的实验数据拟合得到的，橡胶材料的疲劳特性参数包括等效裂纹初始长度、临界撕裂能、撕裂能阀值、临界裂纹扩展速率及应变结晶对疲劳裂纹增长的影响。

1.2 有限元仿真

橡胶是典型的超弹性材料，表现出明显的材料非线性特性，要准确地表征其应力-应变的非线性关系，需要采用应变能函数来描述。论文中进行有限元仿真选用的是Mooney-Rivlin模型，该模型的函数表达式为：

(1)

式中：C10、C01为材料参数，通过拟合材料实验数据得出；D1的取值决定材料是否可压，论文中D1非常小，近似等于0，说明材料是近似不可压缩的；J为变形后与变形前的体积比。

对橡胶制品进行有限元分析的主要目的是获取橡胶构件经历的应变历史，从结果文件中提取所有单元中心的名义应变历史来计算材料的开裂能。由于疲劳分析是基于有限元分析得到的应变历史数据，因此有限元分析的结果直接决定了疲劳分析的准确性。

1.3 疲劳分析

1.3.1 开裂能和撕裂能的计算

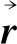
(2)

式中：Wc是通过开裂能增量对裂纹平面的整个形变历史积分得到。

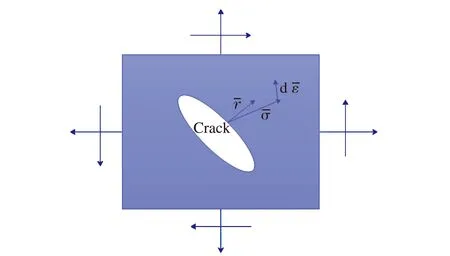
图1 疲劳裂纹平面示意图

从开裂能的定义可知，开裂能不仅与应变历史有关，而且与单元中心所选取的平面有关。由开裂能理论计算每个单元中心所有可能开裂平面在应变峰值点的开裂能，再根据公式(3)计算出所有可能开裂平面的撕裂能峰值。

(3)

式中U为裂纹体受拉时的弹性能；A为裂纹面积；K是与伸长比有关的几何参数；Wc为开裂能；c为外载荷在上次循环结束时的裂纹长度。

1.3.2 结构疲劳寿命计算

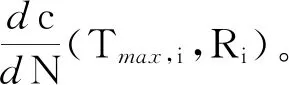
裂纹增长速率计算表达式为：

(4)

其中，Teq、F(R)的表达式为：

(5)

F(R)=F0+F1R+F2R2+F3R3

(6)

开裂平面疲劳寿命计算表达式为：

(7)

式中：R=Tmin/Tmax；Cf为裂纹失稳扩展临界长度；C0为初始裂纹长度；rC为裂纹失稳扩展前段临界速率；Teq为等效撕裂能；TC为裂纹失稳扩展的临界撕裂能；F0、F1、F2、F3是材料常数；函数F(R)是R对裂纹增长率的影响。

2 轨道车辆空气弹簧支座疲劳分析

本文分析的橡胶制品是轨道车辆空气弹簧的附属配件，橡胶支座在疲劳测试中未到达预期使用寿命就出现了严重的疲劳破坏[如图3(c)]。按照前面所论述的分析流程对橡胶支座进行疲劳分析，并优化其结构，以满足产品使用寿命要求。

2.1 橡胶支座材料参数获取[14-15]

本文进行了单轴拉伸、平面拉伸和等双轴拉伸实验，拟合实验数据得到了超弹性本构模型参数，如表1所示。同时，为获取材料的疲劳参数，进行了相关的疲劳参数实验，结果如表2所示。

表1 超弹性模型参数

表2 疲劳实验所确定的疲劳参数

填充天然橡胶是一种具有应变结晶特性的橡胶，必须确定外载荷比例因子R对材料裂纹扩展的影响。利用不同载荷比值下橡胶裂纹扩展实验可以得到不同R因子对F(R)的影响关系，结果如图2所示。

R图2 R因子对F(R)的影响关系

至此，进行橡胶支座有限元分析和疲劳分析需要的所有材料参数都已获取。

2.2 橡胶支座的有限元仿真

基于开裂能理论的橡胶制品疲劳寿命分析需要获取橡胶支座所经历的名义应变历史，实验过程中橡胶支座承受的载荷工况如图3(a)所示。是预加载空气弹簧至其工作高度所施加的垂向载荷，大小为84kN，Y方向加有幅值大小9.5 kN、频率为1 Hz的正弦载荷。此外，橡胶支座还承受与Y同相位的扭转载荷，幅值大小为1.5 kN·m。橡胶支座结构出现1 mm可见裂纹经历的载荷循环次数大约为2.8万次[如图3(c)所示]。

有限元模型如图3(b)所示，有限元分析结果如图3(d)和图3(e)所示，其中支座的最大主应力为14.09 MPa,最大主应变为3.216。

2.3 橡胶支座的疲劳分析

从有限元分析结果中提取橡胶支座每个单元中心的名义应变作为单元的应变历史，利用公式(2)和公式(3)计算出应变历史中单元中心所有可能开裂平面上的开裂能历史，结合式(4)～式(7)计算出所有可能开裂平面的寿命，疲劳寿命最短的平面即为疲劳裂纹扩展平面，提取每个单元的疲劳寿命，结果如图3(f)所示。

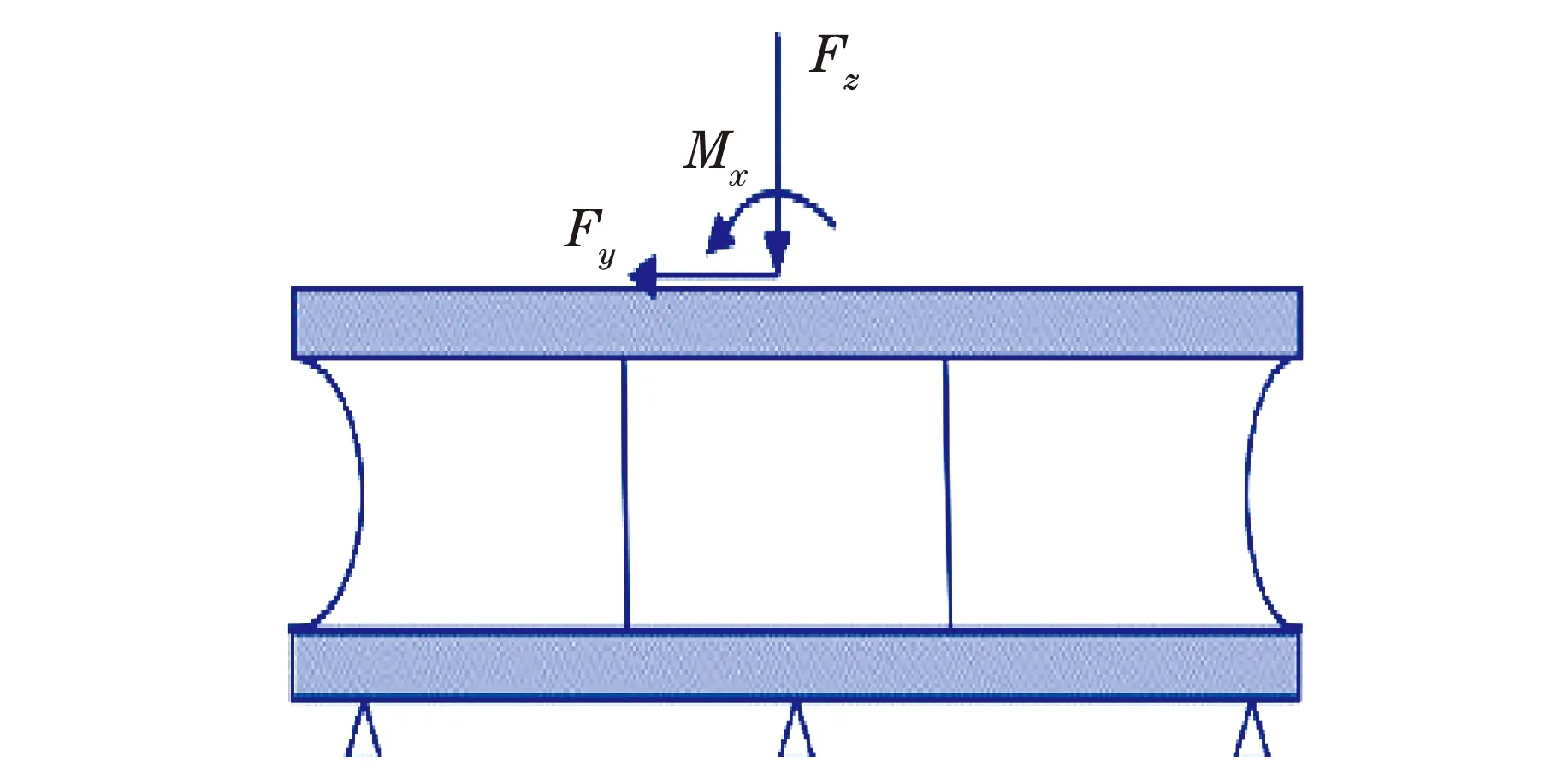
(a) 支座承载工况

(b) 支座有限元模型

(c) 支座真实疲劳裂纹位置

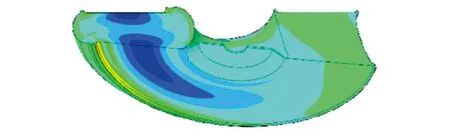
(d) 最大主应力分布

(e) 最大主应变分布

(f) 疲劳寿命分布

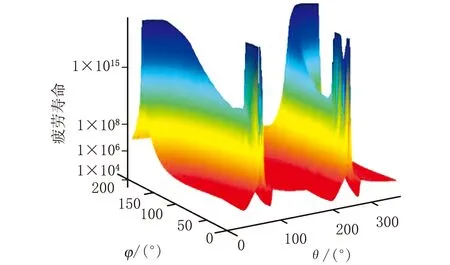
(g) 危险点上所有可能开裂平面的寿命分布

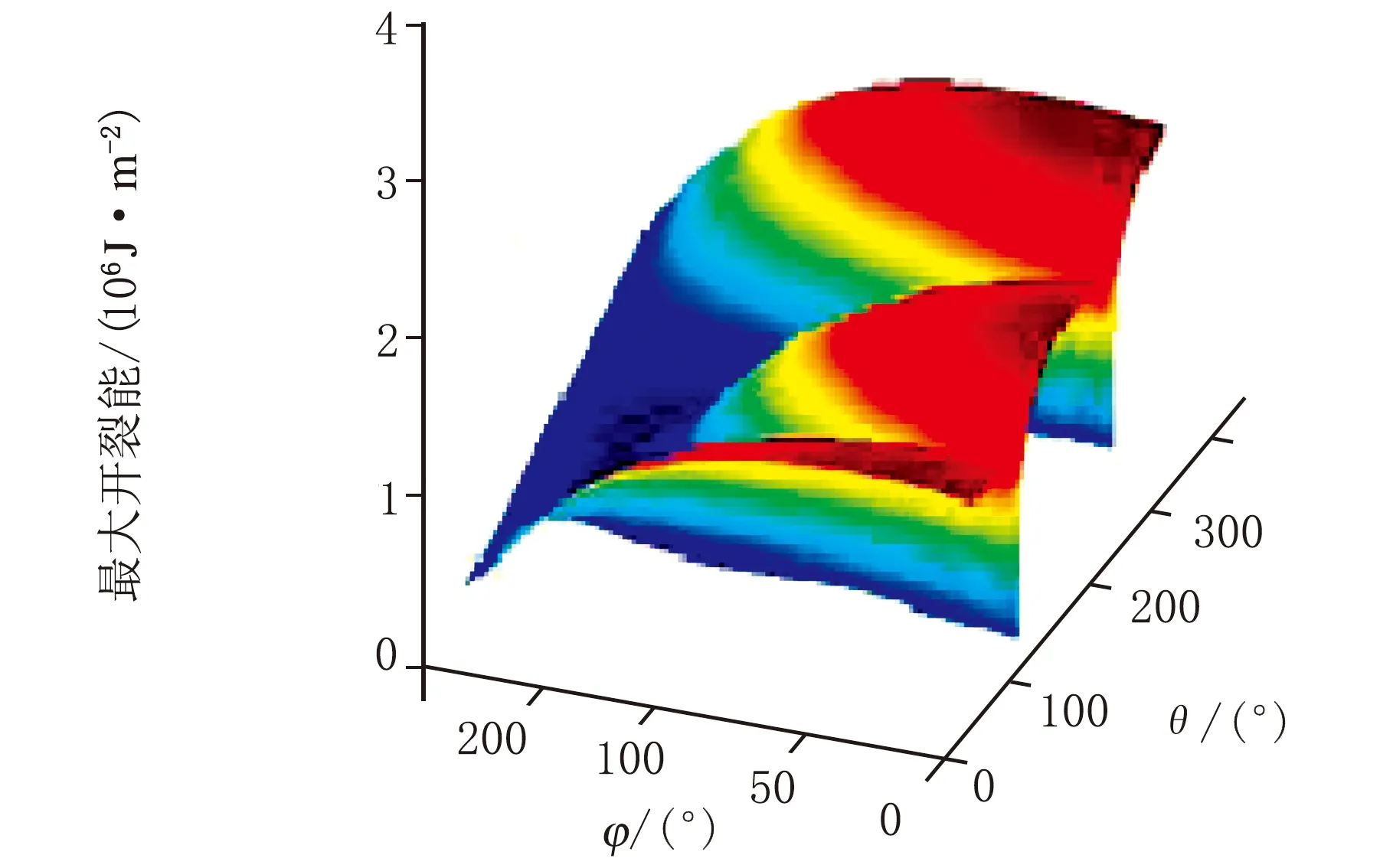
(h) 危险点所有可能开裂平面上的最大开裂能历史

(i) 危险点上所有可能开裂平面上的最小开裂能历史图3 未改进前橡胶支座有限元分析和疲劳分析结果

表3 疲劳危险点数值结果

2.4 结果讨论和分析

通过橡胶支座的疲劳寿命分布图可知，其疲劳危险位置主要集中在下盖板边沿处，且危险点的最小疲劳寿命为23 070次，与实验测得的2.8万次疲劳寿命接近，疲劳裂纹破坏区域与所预测的位置一致，验证了基于开裂能理论的疲劳寿命方法的有效性。

此外，从危险点所经历的开裂能历史图可以得知[如图3(g)～图3(i)所示]，疲劳寿命最短的裂纹平面并没有出现在具有最大开裂能的平面上。事实上橡胶的疲劳寿命不仅与最大开裂能密度有关，与最小开裂应变能密度也有关系。因此，橡胶结构中出现的最大应变区域并非一定是疲劳最危险位置，验证了Mars所提出的应当以疲劳寿命最短的平面作为开裂平面的观点。

3 橡胶支座的疲劳优化

由前文分析可知，该橡胶支座出现严重疲劳裂纹的主要原因是橡胶支座与下底板接触面上存在显著的应力集中。鉴于此，本文设计了一种新的橡胶支座，改进后的橡胶支座结构如图4(a)所示，改进后橡胶支座的有限元模型如图4(b)所示。对改进后的橡胶支座模型进行有限元分析和疲劳分析，分析结果如图4(d)～图4(f)所示。

(a) 改进后的橡胶支座

(b) 改进后支座1/2有限元模型

(c) 橡胶部分1/2有限元模型

(d) 最大主应力分布

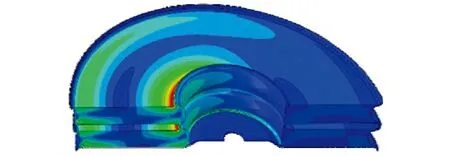
(e) 最大主应变分布

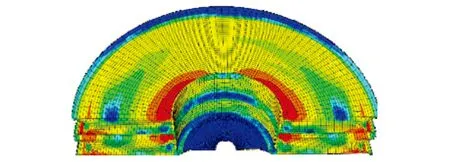
(f) 疲劳寿命分布

φ/(°)(g) 不同平面所经历的CEDMAX

φ/(°)(h) 不同平面所经历的R比例因子

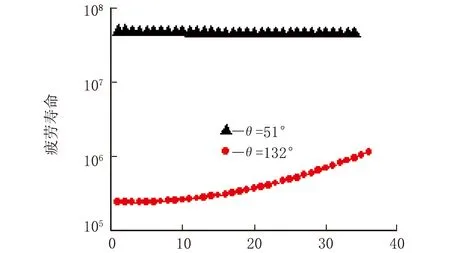
φ/(°)(i) 不同平面上的疲劳寿命

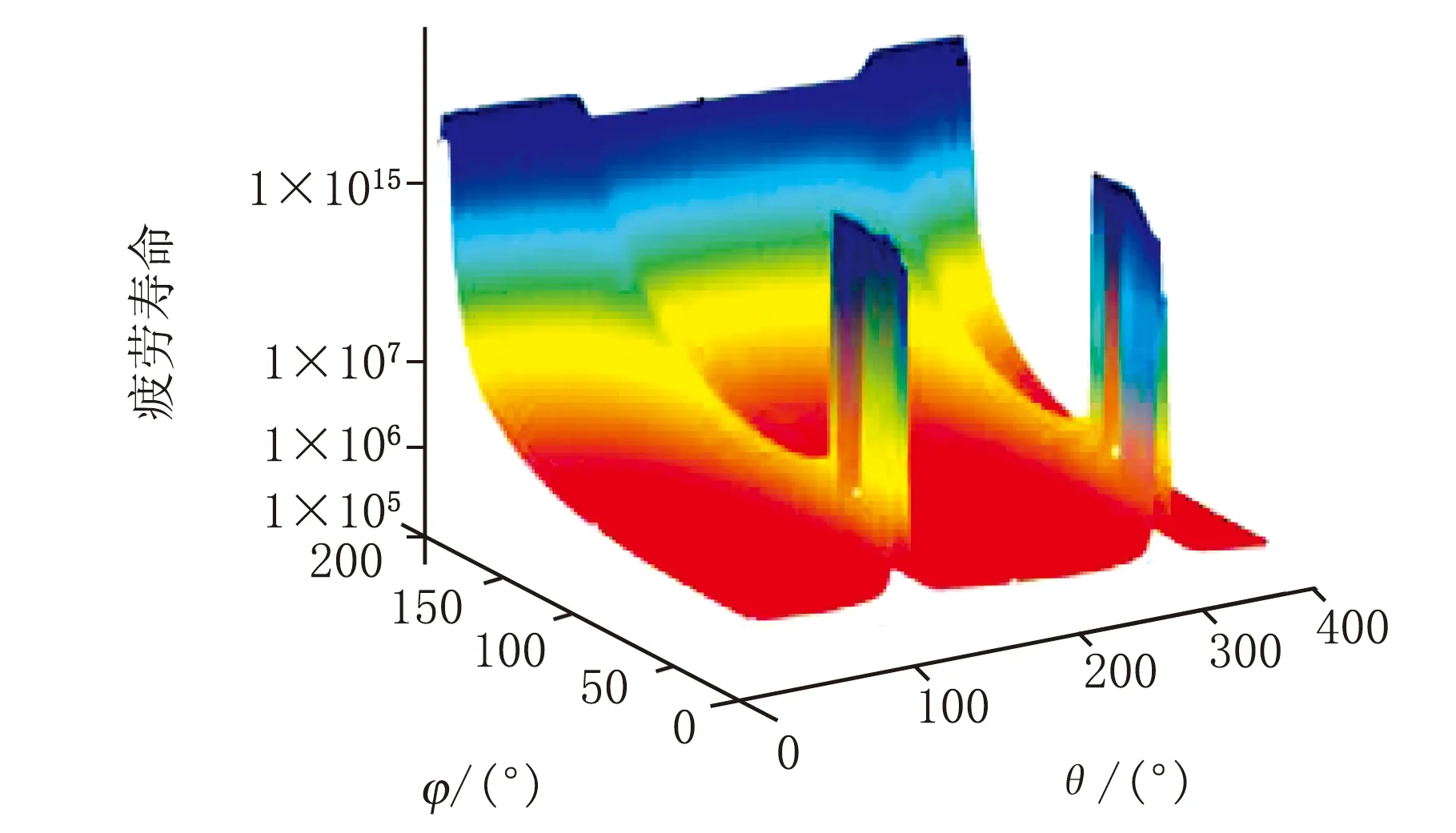
(j) 危险点上开裂平面的寿命分布

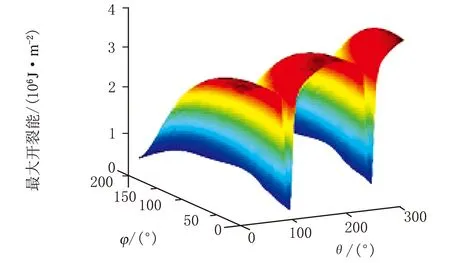
(k) 危险点开裂平面上最大开裂能历史

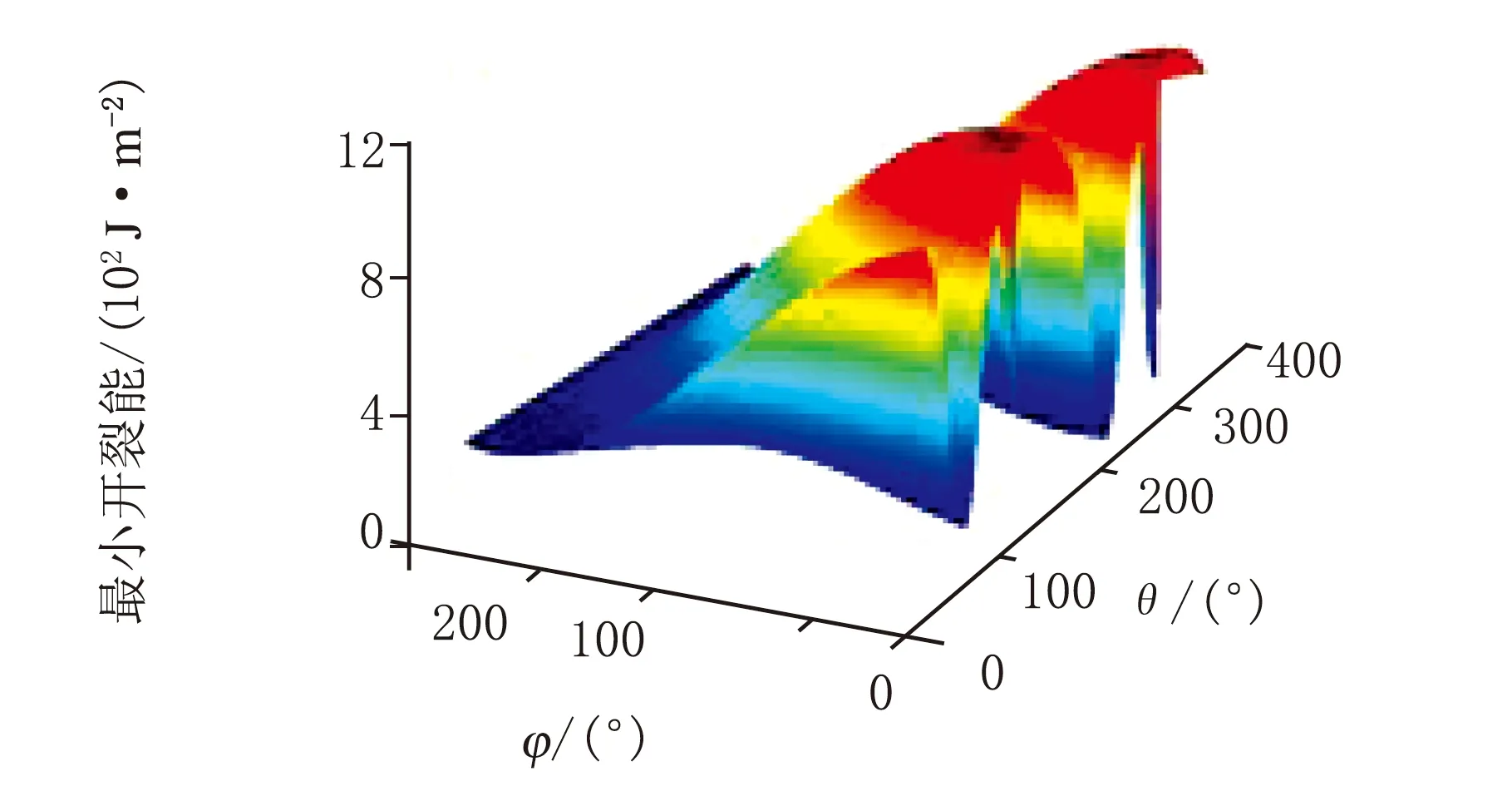
(l) 危险点开裂平面上最小开裂能历史图4 改进后橡胶支座有限元分析和疲劳分析结果

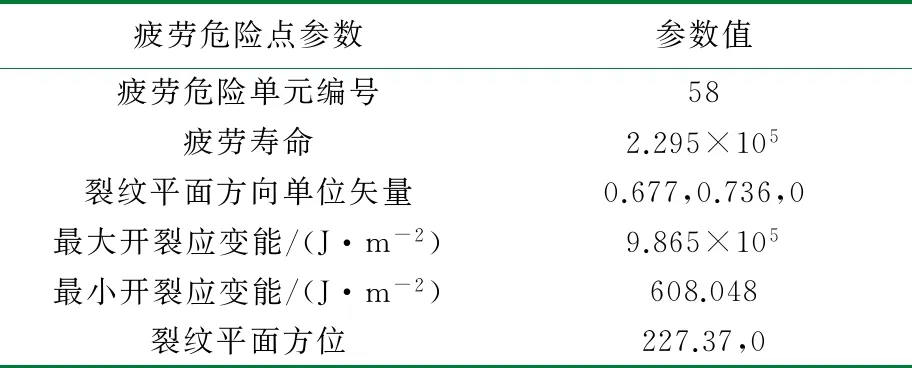
表4 改进后橡胶支座的疲劳和有限元分析结果

对比原橡胶结构，新型橡胶结构的应力集中现象得到明显的改善，最大主应力减少至4.453 MPa,而最大主应变减少至1.307。循环中危险截面所经历的开裂应变能峰值也显著减小，其疲劳寿命上升至229 500万次。图4(g)～图4(i)显示危险点上 132°的平面上所经历的最大开裂能远小于51°平面上的最大开裂能，但由于各平面所经历的R比例因子(即最小CED)不同，前者疲劳寿命明显低于了后者。事实上由于天然橡胶的应变诱导结晶特性，适当提高结构载荷循环下所经历的最小应变(最小开裂能)，可以显著地提升结构的疲劳寿命。

4 结 论

(1) 基于开裂能理论，对空气弹簧的橡胶支座进行疲劳分析与改进，分析结果与实验吻合良好。

(2) 橡胶产品疲劳设计中，应力集中区域的分布在一定程度上能反映橡胶疲劳危险位置的分布状态。通过改善结构应力集中效应，可以显著提高橡胶构件的疲劳寿命。

(3) 疲劳分析结果表明，处于复杂应力状态的橡胶结构，在疲劳裂纹萌生和扩展过程中，裂纹开裂方向和疲劳寿命不仅与最大开裂应变能有关，与最小开裂能也有着密切的联系。因此，具有最大开裂能的平面并非一定是裂纹开裂平面。对于具有应变诱导结晶橡胶而言，适当提高最小开裂能值，可以显著地提高橡胶结构的疲劳寿命。

(4) 基于开裂能量理论的橡胶疲劳分析方法不仅能有效预测处于复杂载荷作用下橡胶构件的疲劳寿命，同时还能获取疲劳裂纹临界开裂平面和开裂方向。

参 考 文 献：

[1] 赵永翔,高庆.估计三种常用应力-寿命模型概率设计 S-N 曲线的统一方法[J].核动力工程,2001,22(1)：42-52.

[2] 沈海军,郭万林.疲劳 S-N 曲线预测的三维断裂力学方法[J].南京航空航天大学学报,2002,34(3)：216-220.

[3] Mars W V.Multiaxial fatigue crack initiation in rubber[J].Tire Science and Technology，2001,29(3)：171-185.

[4] Thomas A G.Rupture of Rubber.V.Cut growth in natural rubber vulcanizates[J].Journal of Polymer Science.1958,31：467- 480.

[5] Saintier N,Cailletaud G,Piques R.Crack initiation and propagation under multiaxial fatigue in a natural rubber[J].International Journal of Fatigue,2006,28(1)：61-72.

[6] Lindley P B.Relation between hysteresis and the dynamic crack growth resistance of natural rubber[J].International Journal of Fracture,1973,9(4):449-462.

[7] 戴永谦,宋希庚,薛冬新，等.裂纹生长方法在橡胶疲劳分析中的应用研究[J].振动与冲击,2005,24(4)：115-119.

[8] Mars W V,Fatemi A.Multiaxial fatigue of rubber：Part I：equivalence criteria and theoretical aspects[J].Fatigue & Fracture of Engineering Materials & Structures,2005,28(6)：515-522.

[9] Mars W V,Fatemi A.Multiaxial fatigue of rubber：Part II：experimental observations and life predictions[J].Fatigue & Fracture of Engineering Materials & Structures,2005,28(6)：523-538.

[10] Mars W V,Fatemi A.Factors that affect the fatigue life of rubber:a literature survy[J].Rubber Chemistry and Technology,2004(77)：391-41.

[11] Rivlin R S,Thomas A G.Rupture characteristic of rubber for tearing energy[J].Polymer Science,1953(3)：291-318.

[12] Mars W V,Fatemi A.A literature survey on fatigue analysis approaches for rubber[J].Rubber Chemistry and Technology,2002(24)：949-961.

[13] Mars W V.Cracking energy density as a predictor of fatigue life under multiaxial conditions[J].Rubber Chemistry and Technology,2002,75(1)：1-17.

[14] 龚科家,危银涛.填充橡胶超弹性本构参数试验与应用[J].工程力学,2009(6)：193-198.

[15] 胡小玲,李明,刘秀,等.炭黑填充橡胶超弹性本构模型的选取策略[J].工程力学,2014,31(5):34-42.