小学思维训练中数学建模思想的运用探究

闽江学院数学系 贤 锋 林 鑫



小学思维训练中数学建模思想的运用探究

闽江学院数学系 贤 锋 林 鑫

该文论述数学建模思想在小学思维训练中的运用，通过结合一部分小学数学思维训练的典型例题，依据大学建模知识，应用数学建模思想分析和解决这些问题，达到训练小学生数学思维的目的。

数学建模思想 小学 思维训练

1 概述

数学是研究数量、结构、变化以及空间模型等概念的一门科学。由此可见，数学模型是数学这门科学中尤为重要的一部分。数学建模是一个世界性的研究课题，它起源于上世纪70年代末的英国剑桥大学[1]。随着科学技术的快速进步，数学模型受到现代人的关注越来越多，无论是生产、工作、各种活动，都离不开数学建模。而小学数学教学也应当与发展要求相适应，充分运用建模思想，培养小学生建模的意识和能力[2]。

建模思想强调的是对实际问题的抽象和概括，而小学阶段的数学教学以实用性为主，突出了数学知识在生活中的应用。在小学数学教学中，由于学生的认知水平、知识程度不够，难以对学生展开数学建模的教学。在2011版《数学课程标准》中，提出了培养学生体会数学建模的过程，树立模型思想，但是在教学操作上的指导意见比较罕见。如何通过实践体现课程标准的理念，正是值得我们思考的一个重要问题。数学思维训练虽然在这些年来受到广泛争议，但不可否认的是，在训练过程中很好地体现了数学建模思想的广泛运用。本文以数学建模思想为立足点，尝试探究其在数学思维训练的运用，通过例题分析，结合大学数学建模知识，为小学思维训练甚至小学数学建模教学提供一些应用基础。

2 小学思维训练中的数学模型

2.1 小学数学建模

小学数学建模的主体是小学生，是利用小学数学系统中的原理、法则等建立的数学模型。在小学，由于小学生的知识水平、认知能力有限，进行数学建模教学具有鲜明的阶段性、初始性特征，不能有难度太高的专业知识，即要从学生熟悉的生活和已有的经验出发，讲究有趣味性并且容易理解，具有一定的实用性，和生活紧密相关，引导他们熟悉将实际问题初步抽象成数学模型并进行解释与运用的过程，进而对数学学习产生更加深刻的理解[3]。

2.2 小学数学思维训练

数学思维训练（包括奥赛）在小学数学教学中还是有一定积极意义的，只是目前数学教育把思维训练这一活动当作考量学生的工具，而不是真正为了学生的发展。数学思维训练可以激发学生对数学的兴趣，体验到学习数学的意义和快乐。同时数学思维训练也有助于挖掘学生的数学潜能，训练出良好的数学思维，培养良好的数学品质，让学生获得发挥创新能力的空间，培养学生灵活运用数学的能力，促进人才的早期培养。

2.3 建模思想在数学思维训练中的应用举例

2.3.1几何模型

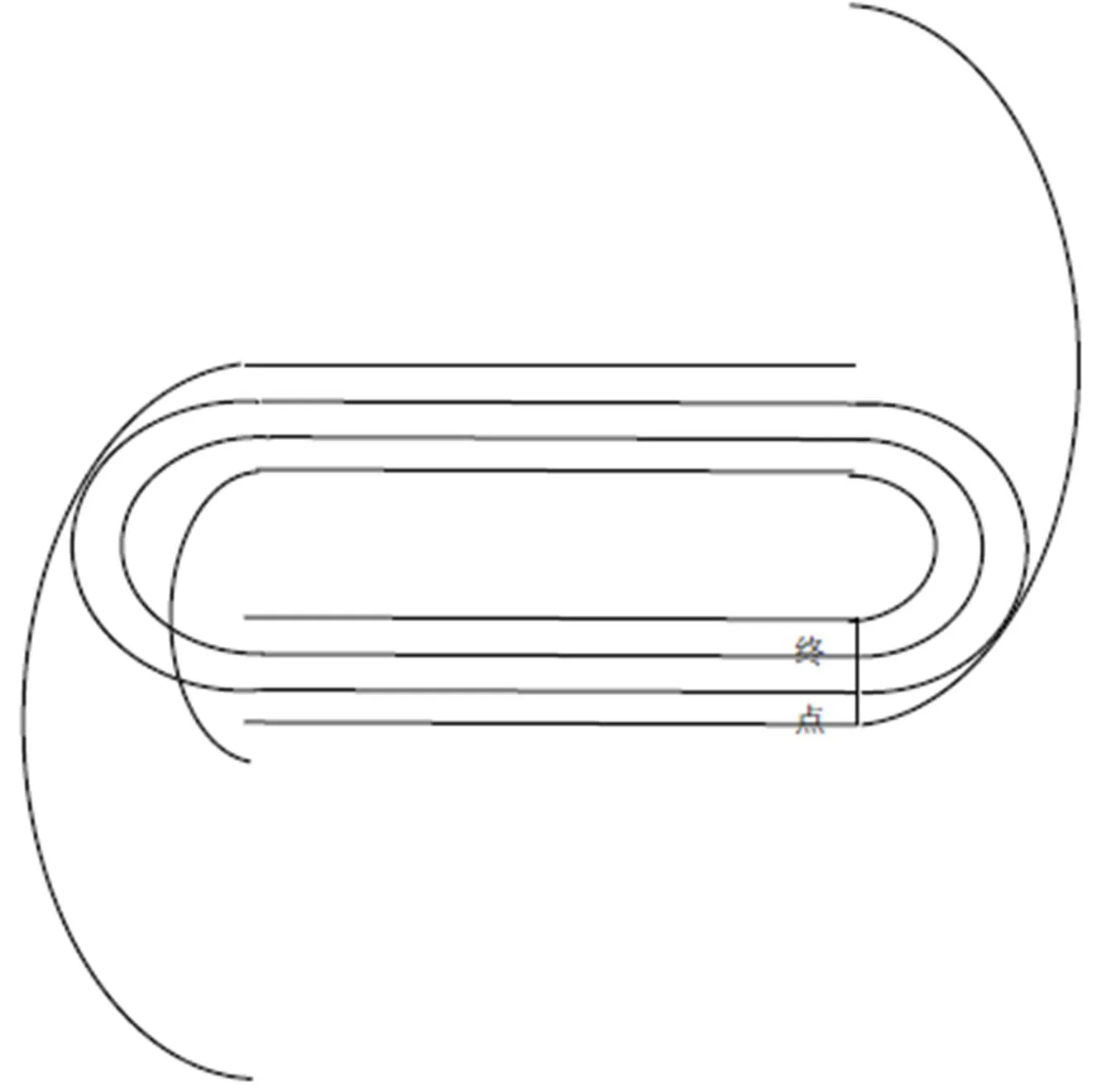
图1

分析 由常识可知，最内道为400米。所以在最内道应从终点处开始起跑。由图1可知，跑道在直道处长度是一样的，所以长度的差异就在弯道处，所以我们来分析左右两个半圆跑道。由于左右两个半圆形对称。现在我们把左右跑道从跑道中分离出来，得到图2。把两个半圆组合起来得到图3。

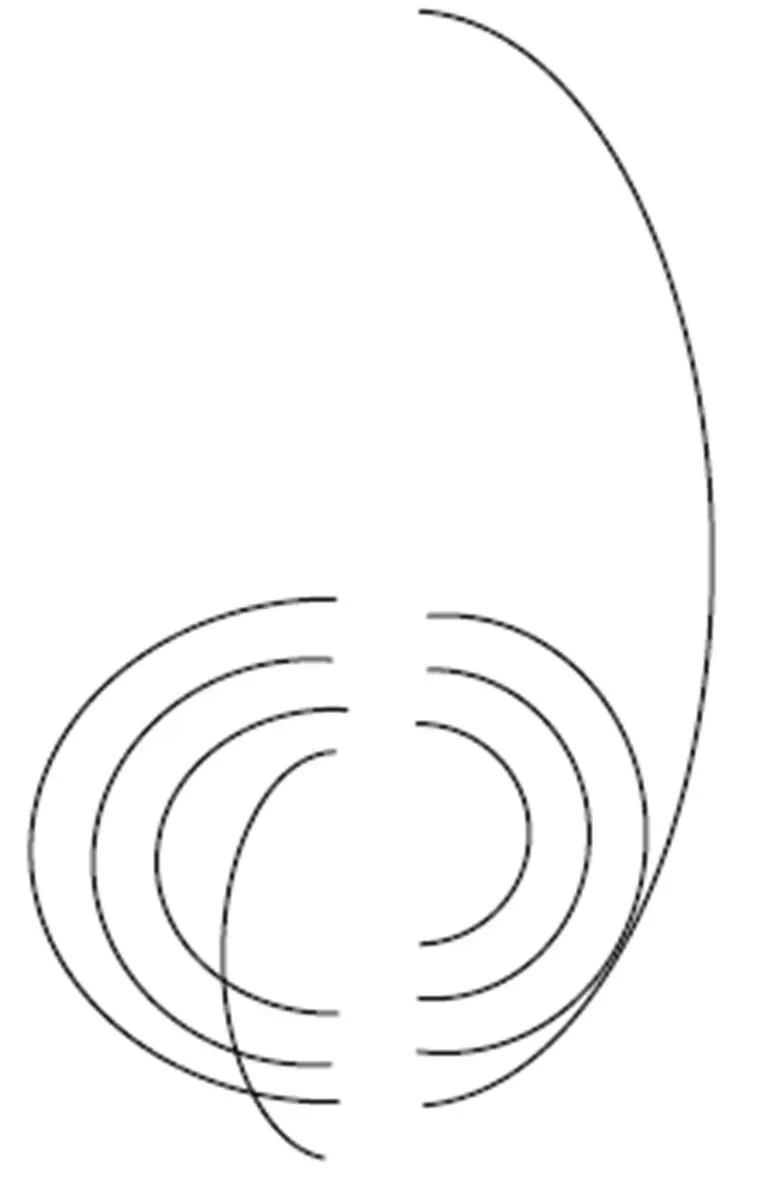
图2

图3

不妨假设，运动员跑步时，都跑在各自跑道的中间位置，即图3中的虚线。所以如果三位运动员在各自跑完自己所在的跑道，他们之间的赛程差距就是图3中虚线的三个圆形轨道周长之差。设最内道所对应的跑步轨迹半径为，则中间道所对应的跑步轨迹半径为(R+1)，最外道所对应的跑步轨迹半径为(R+2)。最内道的在弯道跑过的路程S1为2，而如果在中间道跑完跑道全程的路程为2(1)，最外道跑完跑道全程的路程为2(2)。

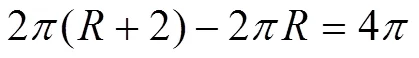
所以最内道次运动员的起点设置在终点线，中间道次运动员的起点应该设置在终点线前2米(即6.28米处)，最外道运动员的起点应该设置在终点线前4米(即12.56米)处。

正如本题所示，小学思维训练中的几何模型是比较常用的，这一类题目总是和生活场景结合一起。在生活中找到几何问题的对象，本题为跑道，通过对跑道的分析和简化，将实际问题转化为几何问题，运用数学中的几何知识，进行分析，得到数学结果，代入实际问题，得到实际结果。最后将建模得到的结果，代入实际对象（跑道）进行检验。

2.3.2函数模型

例2 甲与乙同时从A出发到B，甲一开始以时速4km的速度走路，中途改乘时速42km的公交车。乙则是以时速12km的速度骑自行车。结果甲比乙早到了10分钟，参考图4，求A、B两地间的距离。

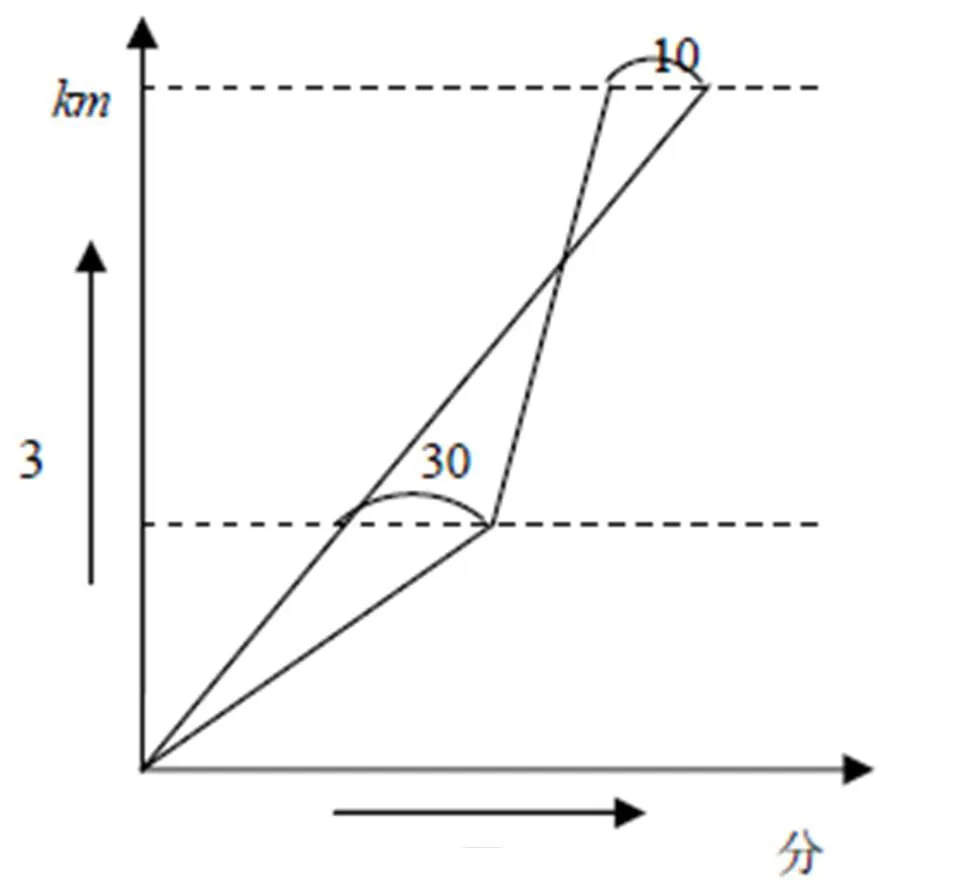
图4

图5

分析本题可以将图4，以为原点，路程为轴，时间轴为轴建立坐标系如图5。

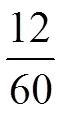
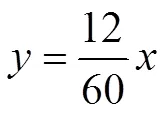
30，则点的坐标为(45,3)

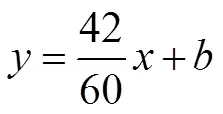
所以点坐标为(71,14.2)

由于横坐标表示时间，纵坐标表示距离。从A地到B地，乙花了71分钟，以时速12km，行驶的路程为14.2km。所以A、B两地相距14.2km。

本题为路程问题。通过对题中所给的路程图示，结合函数知识，建立函数图像的模型。把速度用斜率表示，纵坐标表示路程，横坐标表示时间，建立直角坐标系。通过题中所给的已知条件，得到函数图像中点的坐标。通过点坐标和函数解析式相互代入计算，得到我们需要的点坐标，它的纵坐标就是我们需要的两地距离。将得到的结果代入原题检验，检查是否满足题意。

2.3.3图论模型

例3 如图6，这是一张路线图，由于路况不同，汽车通过这些路线时，速度也不同。每段路上的数是汽车通过这段路所需的时间（单位：分钟）。请问汽车从A点开往B点，最快需要多少分钟？

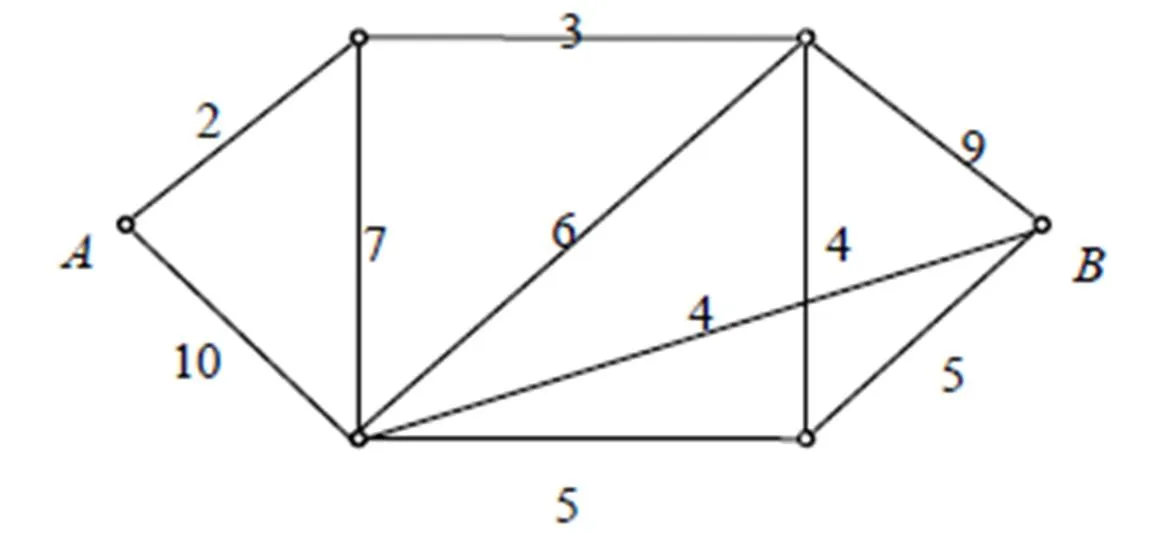
图6

第一轮（T）标号：

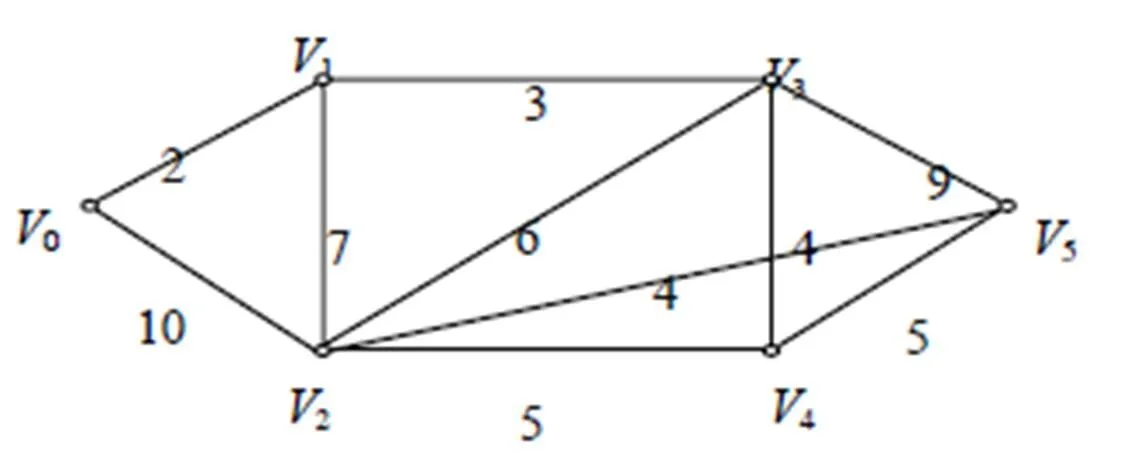
图7

第一轮标号结束，0变成标号，即1，进行下一轮重新标号。

第二轮（T）标号：

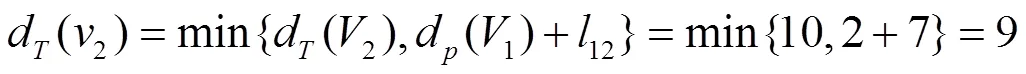
3变成符号，此时0,1,3。第二轮标号结束。

第三轮（T）标号：

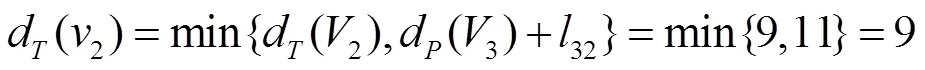
第四轮（T）标号：

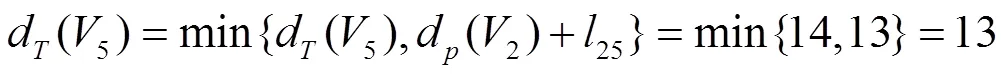
至此，全部结点都已标号。

所以从0到5到最短路长13，最短路是0→1→2→5。

将模型还原到实际问题，即从A点到B点最快需要13分钟。

这是数学思维训练中一道简单的规划问题。由于该问题求的是两定点的最快路径（通过两定点间最短时间），即时间的最短路径。所以我们可以结合图论中最短路径的知识，建立图论模型。通过算法，计算出模型中的最短路径，即实际问题中时间的最短路径。结合路线图，可以检验该路径是否最快到达，即可检验出模型的可行性。

2.3.4线性代数模型

例4 甲、乙各有100颗苹果。如果进行这样一次交换：甲取自己苹果的40%给乙，而乙取自己苹果的70%给甲。问，进行一次交换后，甲乙各有多少个苹果?在第一次交换的基础上，再进行这样一次交换，结果又如何?

这是数学思维训练中关于分数和百分数的题目。这个问题通过可以建立线性代数模型来解决：

由题可写出2×2矩阵，表示一次交换。

在矩阵中，

11=0.6表示进行一次交换，甲剩下自己的(1-40%)=60%；

12=0.7表示进行一次交换，甲获得乙的70%；

21=0.4表示进行一次交换，乙获得甲的40%；

22=0.3表示进行一次交换，乙剩下自己的(1-70%)=30%

（即第一列表示甲原来的苹果，第二列表示乙原来的苹果；第一行表示交换之后甲的苹果，第二行表示交换后乙的苹果）。

则一次交换后，甲、乙的苹果数表示为：

即交换一次之后，甲的苹果数量为130，乙的苹果数量为70。

所以在第一次交换的基础上再进行一次交换后的结果如下：

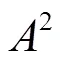
所以在第一次交换的基础上，再进行一次这样的交易，结果是：甲的苹果数量为127，乙的苹果数量为73。

这个问题虽然是简单的百分比计算。但是考虑的要进行多次同样的交换，我们可以通过建立线性代数模型，将交换关系用矩阵表示，用二维向量表示两人各自的苹果数量，通过计算矩阵和向量的乘积，得到交换后的二维向量，即得到交换后甲、乙两人的苹果数量。同理，进行第二次交换也一样的。最后，用得到的结果检验模型的正确性。

2.3.5数学规划模型

例5 某地区有甲、乙两个自来水厂，分别向A、B、C三个村庄供水。按需求，A村需要45吨，B村需要75吨，C村需要40吨。现在甲自来水厂存水60吨，乙自来水厂存水100吨。甲、乙两厂与A村、B村、C村的距离如图8所示。已知每吨水每千米输送的费用为1元，怎么安排可以使输送费用最低?并求出最低的费用。

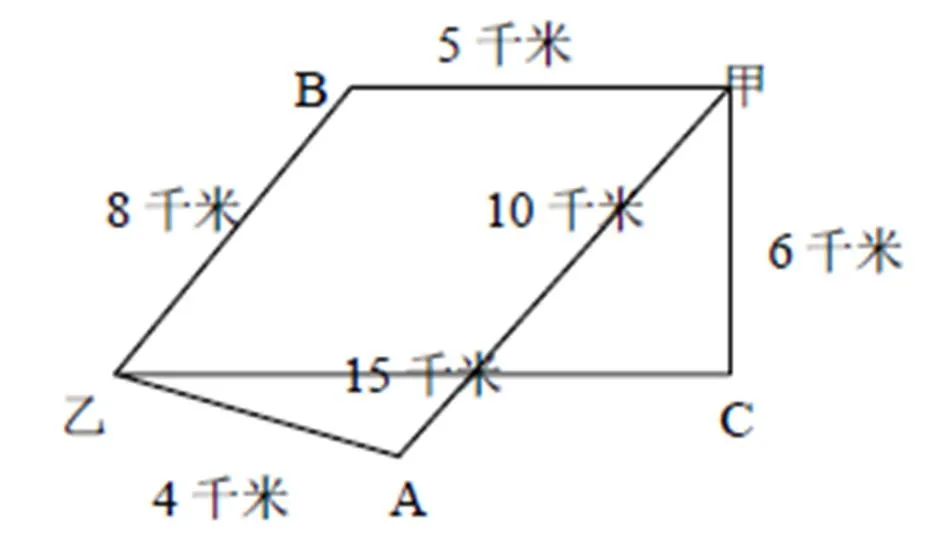
图8

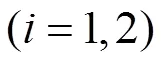
模型求解(输入软件)：

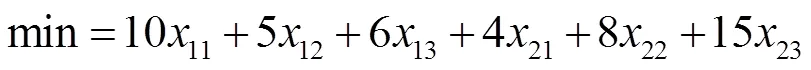
求解得到的输送方案为：甲自来水厂向C村输送40吨，向B村输送20吨；乙自来水厂向A村输送45吨，向B村输送55吨。

3 结论

培养学生的数学建模思想是素质教育的要求。虽然数学建模知识只有在大学期间才会正式涉及，但是对于处于小学阶段的学生来说，此时处于能力发展的重要阶段，也少不了数学建模思想的学习。也许在许多人的认识中，数学思维训练只是锻炼学生的解题能力，培养学生的解题技巧，缺乏对问题本质的分析。正如本文所述，数学建模思想也可以广泛运用在小学思维训练中。

数学建模教学可以培养学生的洞察能力、数学语言翻译能力、综合应用分析能力、联想能力及各种当代科技最新成果的使用能力[4]。笔者建议在小学数学思维训练教学中，教师应该加强对学生数学建模思想运用的引导，让学生真正学会分析问题，从问题的本质来思考问题，而不仅仅是简单地对解法进行学习，这样才能实现《数学课程标准》中的既定目标。

[1] 郭淑英. 对数学建模的几点认识[J]. 山东教育，2010(28)：43.

[2] 王亮. 建模思想在小学数学中的应用探讨[J]. 教师，2012(15)：43-44.

[3] 陈永琴. 对数学建模的几点思考[J]. 数学学习与研究，2013(14)：136.

[4] 刘瑞芹，王文祥. 数学建模[M]. 北京: 煤炭工业出版社，2009.