砂浆泵节能调速控制研究

张茂杉，王幼民，胡 建

安徽工程大学机械与汽车工程学院，安徽芜湖，241000

1 研究背景

随着科学技术的发展与人们节能环保理念的提高，工业生产过程越来越注重资源节约和环境保护。砂浆泵是专为输送含有细颗粒的腐蚀性介质而设计开发的，在化工领域应用广泛，对砂浆泵进行节能控制，不仅有利于实现精细化生产，而且对于资源节约具有十分重要的意义。

目前，国内外学者对泵的节能调速控制作了大量的研究。文献［1］对于大功率的泵和风机的节能调速采用了串调和无刷双馈电机的方法，该方法误差较大，难以实现较高精度的控制。文献［2－3］对于泵的调速系统的研究是通过建立泵的调速过程状态参数的变化模型来建立调速过程的方程组，并通过程序仿真对模型进行分析。文献［4－5］对于泵的调速系统的研究主要集中在变频调速方面，没有采取更加合理的控制算法。文献［6］对于风机和水泵的调速运行是通过改善阀门的开度与管网曲线来实现调节流量的，该控制方法在一定程度上限制了机器的性能，影响泵的寿命。文献［7－10］采用极值法分析了变频中央空调的液压泵系统及热泵系统，该方法需要建立各种损失与几何参数之间的关系，对于很多非线性系统很难实现。

随着控制理论以及控制技术的发展，人们越来越倾向于采用智能控制的方法，尤其是神经网络的控制算法，由于其良好的容错性以及全局逼近的学习方法，具有较好的泛化能力，因此应用更加广泛。文献［11］研究了基于神经网络的机器人的智能控制算法，并指出神经网络控制与模糊控制相结合的控制方法是目前机器人智能控制的发展方向。文献［12］主要研究了基于BP神经网络的深水自升式海洋平台的智能控制模型，结果表明BP神经网络的控制对于海洋平台具有良好的稳定性效果。

本文根据砂浆泵的工作原理及生产状况确定了砂浆泵的传递函数，并设计了基于BP神经网络的智能控制方法，对流量控制系统的静态性能和动态性能进行了理论分析及程序仿真。为了提高流量控制系统的性能，采用了极点配置的优化方法得到最佳的传递函数，并且通过极点配置前后的对比，可以看出控制系统的性能有了很大的提高。通过实验验证，可以看出上述控制方法使控制系统的控制性能得到提高，达到了理想的控制效果，完全满足现实的生产要求。

2 砂浆泵流量控制系统数学模型建立及控制方法研究

2.1 砂浆泵流量控制数学模型的建立

砂浆泵是离心泵的一种，它与普通供水离心泵的区别在于过流部件全部采用超高分子材料制成，因此砂浆泵的数学模型［13］与普通离心泵系统相同。由于很难建立精确的离心泵系统的数学模型，故采用其近似模型进行仿真研究。由离心泵系统的特性可知，通常将泵由停机状态到稳定状态的过程分为压力上升过程和恒压过程。压力上升过程近似为一个大时间常数T1的一阶惯性环节；恒压过程中，压力可认为基本保持不变，是一个纯滞后过程。变频器和电机可近似等效为带死区时间，且时间常数为λ的一阶惯性环节。在异步电机变频调速系统中，要选择最佳的起动频率，使起动转矩最大而电流尽可能小。一般电动机的最佳起动频率大约在12.5～25Hz的范围内，因此，在最佳起动频率之前的频段是系统的死区范围。系统中其他控制和检测环节，如继电器控制转换、压力转换等的时间常数和滞后时间与原供水系统执行机构的时间常数和滞后时间常数相比可忽略不计，均可等效为比例环节。

图1 控制系统方框图

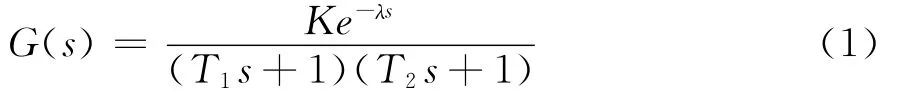
因此，离心泵系统的数学模型可等效为带纯滞后、死区两个惯性环节串联，用如下式子表示：式中，K为系统总增益；T1为系统惯性时间常数；T2为变频器及电机时间常数；λ为系统纯滞后时间常数。本文研究的砂浆泵具体参数，取K＝20，T1＝0.174，T2＝31.826，系统纯滞后时间常数λ＝1.5。所以砂浆泵的数学模型为：

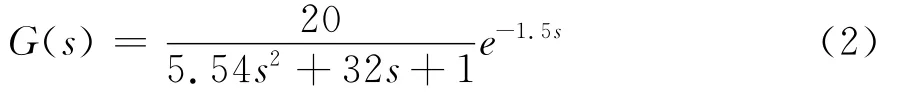
2.2 砂浆泵节能调速控制系统控制方案研究

由于泵的流量控制是非线性的对数关系，传统的PID［14］控制方法只能对线性关系进行有效控制，而且对数学模型的准确性要求十分严格，本文采用智能控制与传统的PID控制相结合的方法，能有效解决非线性问题。

在智能控制与传统PID控制相结合的基础上，采用BP神经网络控制与传统PID相结合的方法，BP神经网络对非线性具有任意逼近和自学习性，为系统辨识，尤其是非线性动态系统的辨识提供一条十分有效的途径，它与PID控制相结合，可以弥补PID控制的不足。该系统由微处理器、流量传感器、A／D转换器、接口电路、泵组成。泵的转速为输入量，泵的转速为输出量，实质为泵的流量定值控制系统，微处理器实时控制计算机，变频器和砂浆泵作为系统的执行机构，用变频器控制水泵电机的转速，使泵的流量符合工艺生产要求。

本文将基于BP神经网络的智能控制方法用于砂浆泵的节能调速控制系统中，调节流量控制系统的参数，使控制系统的性能达到理想状态。为了得到最佳控制性能，再采用极点配置的方法，对原系统进行优化，仿真与实验表明控制效果达到了最佳。

3 砂浆泵流量控制系统的性能分析

3.1 砂浆泵流量控制系统的稳定性分析

控制系统的稳定性是系统进行运行及设计的首要前提。对一个不稳定的系统无法进行控制分析，因此，只有当控制系统是稳定的时候，才有价值分析和研究控制系统的其他问题，比如只有计算过稳定性的系统，才可以进行控制系统的稳态误差的计算。控制系统稳定性的分析方法有很多，如奈奎斯特稳定判据、对数判据以及李亚普诺夫稳定性判据等。本文采用李亚普诺夫稳定性判据，并结合Bode图，对砂浆泵的流量控制系统进行稳定性分析。李亚普诺夫稳定性判据是俄国数学家和力学家A.M.李亚普诺夫1892年创立的用于分析系统稳定性的理论，在分析稳定性的问题中应用广泛。

有系统的状态方程为x＝Ax＋bu，式中x为n维状态向量，A为n×n维常系数矩阵。根据李亚普诺夫稳定性判据，若存在一个正定矩阵P，使得系统满足AT＋P.A＝－I，则表明该系统在x＝0处的平衡状态是满足大范围内渐进稳定的，式中I为n维单位矩阵。由（1）式得：

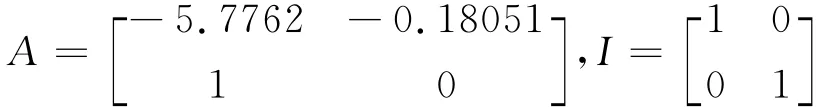
代入上式计算得：

则P为正定矩阵满足稳定性判据，系统稳定。

由MATLAB软件仿真得到流量控制系统的Bode图（图2）。

图2 砂浆泵流量控制系统的Bode图

3.2 砂浆泵控制系统的能观性与能控性分析

基于状态空间分析的系统的可观性与可控性是控制系统中非常重要的概念。所谓控制系统的可控性就是指控制系统的状态是可以控制还是不可以被控制的；系统的可观测性就是指系统状态的变化能够由输出检测反映出来，还是不能由输出检测反映出来。

在设计控制系统之前，确定系统的能观能控性是十分重要的，因为在设计一个最优的控制系统之前必须知道系统的能观测性与能控性。系统的能观能控性是确定最优控制是否有解的先决条件。因此，系统的可观测性与可控性对系统的设计至关重要。

3.2.1 能控性分析

则控制系统能够满足能控性判据，控制系统是能控的。

3.2.2 能观测性判据

根据能观性定义，系统的完全能观性是指在指定的时间之内，根据能够测量到的输出量y（t）唯一的确定系统的初始状态x（0）。对于上式如果秩小于n，则不能保证由输出值可以确定初始量。因此控制系统如果是可观的，则其秩必须为满秩。由（2）式A代＝ ［1 0］，可得能控性矩阵：入上式可得能观测性矩阵的秩：

则满足能观性判据控制系统是能观的。

3.3 采用PID控制方法对砂浆泵流量控制系统进行控制

PID控制器是由比例、积分与微分组成的，可以通过调节Kp比例系数、Ti积分时间周期与Td微分时间周期来调节系统，从而达到设计要求。在实际工业生产中，一般的系统都不是线性而是非线性的，在使用PID调节时，可以将系统简化为线性系统，本文采用经验试凑法得到PID参数Kp＝0.5，Ki＝0.0145，Kd＝0.099。

由（2）式的流量控制系统传递函数：

则对流量控制系统进行Simulink系统建模，采用PID控制模块得到系统的控制模块图（图3）。

采用经验试凑法调节PID参数得当为如下值时系统的性能达到最好。

图3 Simulink的控制模块图

程序的运算结果如图4所示。

由图4也可以看出控制系统是稳定的。

3.4 基于BP神经网络的流量控制

BP神经网络是Rumelhart.D.E和Mcclelland.J.L等人于1986年提出的多层前馈网的反向传播算法，基本BP算法包括两个方面：信号的前向传播和误差的反向传播，即计算实际输出时，按从输入到输出的方向进行，而权值和阈值的修正，则从输出到输入的方向进行。该网络并不依赖模型，只要有足够多的隐层和隐结点，BP网络可以逼近任意的非线性映射关系，其输入与输出之间的关联信息存储于连接权中。由于连接权的个数很多，个别神经元的损坏只对输入输出关系有较小的的影响，所以BP网络具有较好的容错性，而且BP网络的学习算法属于全局逼近的方法，因而具有较好的泛化能力。

在砂浆泵的流量控制系统中，需要进行控制系统的前向和反向计算，流量的实际输入信号从输入到输出方向正向传播，从而控制电动机的转速，以达到流量控制的目的；权值和阈值的修正，则从反向传播，调节控制信号，使偏差控制在最小的范围内。

3.4.1 BP神经网络的计算机仿真

由系统的传递函数

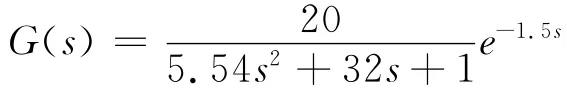
得到利用MATLAB进行程序仿真程序运行结果，如图5所示。

由图5可知，系统的过渡过程平稳，由于传递函数有延时的存在，所以稳定时间需要8～9秒，而且过渡过程曲线没有超调量存在，运行平稳。

图5 系统的过渡过程曲线

由图6可知，在程序运行开始时，系统中存在较大的误差，随着时间的推移，误差逐渐减小，直到最后在9秒钟左右时，误差为零。

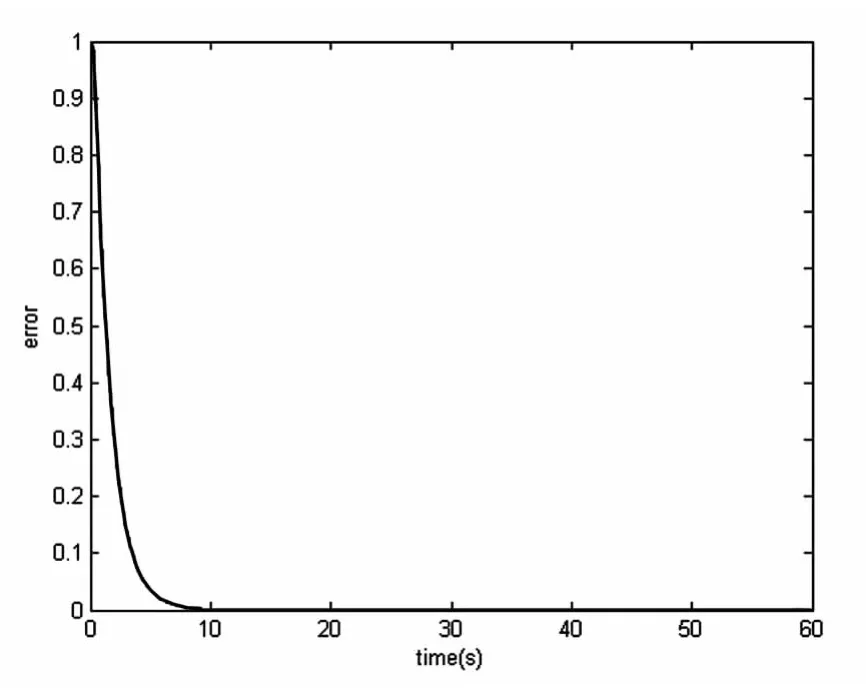
图6 系统的反应误差曲线

由图7可知，kp参数在3秒左右时稳定在0.94左右，ki参数在七八秒时稳定在0.003 1左右，kd参数在7秒钟左右时稳定在0.72左右。图像的过渡过程比较平稳，没有大的超调量，这表明系统的运行是比较平稳的。

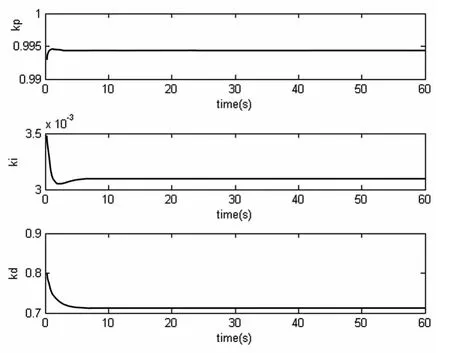
图7 PID参数稳定过程曲线

4 砂浆泵节能调速控制系统的极点配置优化

在控制系统中，无论是镇定系统，还是跟随系统，都必须符合相关的性能要求。控制系统的动态响应主要是由它的极点位置决定的。因此，控制系统的设计就是应用状态反馈，使得控制系统具有期望的极点配置，从而改善系统的性能。系统的极点配置就是在给定系统的期望极点之后，如何通过某种方法来达到期望的极点。

对于控制系统而言，在采用状态反馈之后，可以实现闭环极点的任意的配置，即通过状态反馈的方法，使闭环系统的极点位于预先设定的位置之上。

4.1 砂浆泵流量控制系统的极点配置

4.1.1 控制系统极点配置的综合性能指标

系统的输出超调量Mp≤5%，峰值时间tp≤0.5 s，系统频宽ωb≤10rad／s，跟踪误差为ep＝0（对阶跃信号）。

4.1.2 确定控制系统期望的极点

系统的期望极点数n＝2，系统的性能主要是由主极点决定。根据二阶系统的关系式，确定主导极点。

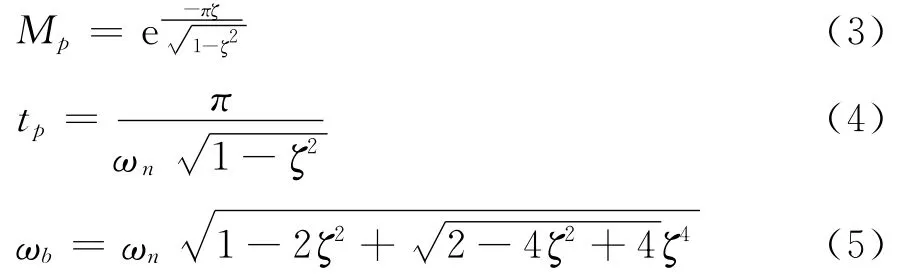
式中，ζ和ωn为此二阶系统的阻尼比和无阻尼固有频率。

tp＝≤0.5s，当ζ＝0.707时，选ωn＝10rad／s

这样，便定出了主导极点s1，2＝－ζωn±jwn，因此确定的期望极点为：

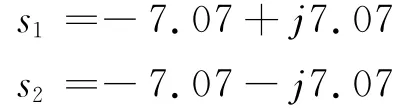
由系统的期望极点可以求出系统的特征方程：

则系统的原传递函数：

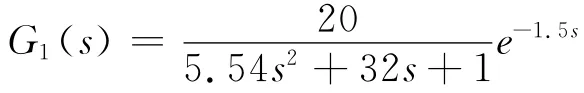
经过极点配置后的传递函数为：

4.1.3 确定控制系统的状态反馈增益矩阵K

由（2）式得流量控制系统的传递函数的特征多项式为s2＋5.031s＋0.152，则a1＝5.031，a0＝0.152。由（6）式得流量控制系统进行极点配置之后的特征多项式为s2＋14.1s＋1，则b1＝14.1，b0＝100。

4.2 极点配置前后的流量控制系统的响应

使用Simulink程序仿真比较极点配置前后的过渡过程，由（2）式、（6）式得程序方框图，如图8。

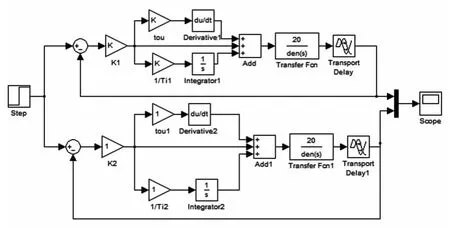
图8 极点配置前后的Simulink方框图

程序运行结果如图9所示。

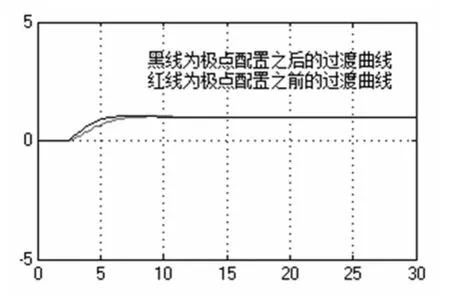
图9 极点配置前后的Simulink结果图

从图9中可以看出，极点配置之后，砂浆泵的流量控制系统在6至7秒的时间内就可以稳定，而且过渡曲线的过渡过程很平稳，几乎没有超调量。而极点配置之前的过渡曲线要在10秒钟之后才会稳定，这说明极点配置之后流量控制系统的性能有很大的提高。

5 实验验证

本文通过对砂浆泵节能调速控制的原理分析，确定了多种流量控制方法，如纯PID控制方法、极点配置优化与PID相结合的控制方法以及基于BP神经网络的智能控制方法。通过程序仿真图形的比较可以看出，使用极点配置优化之后的控制系统的过渡曲线最优。这个实验通过S7－200PLC对极点配置优化与PID相结合的控制方法进行编程，并结合Wincc flexble组态分析和Smart700IE触摸屏对泵的流量进行控制研究。

首先将编好的程序下载到S7－200PLC中，打开实验平台的控制开关，进入控制界面，对泵的流量的上限和下限进行设定，当流量高于上限、低于下限时，系统会进行自动报警，设定泵的流量的上限值为3.5m3／h，流量的下限值为3.4m3／h，按下“启动按钮”，当系统稳定后，流量稳定在3.411m3／h，可以看出，流量的稳定值与设定值之间的差值是很小的，因此这种控制方法达到了预期的控制效果（图10）。

图10 实验装置图

按下“停止按钮”，则系统立即停止工作，点击进入“流量的趋势图界面”，切换到流量的趋势图（图11），控制系统的流量曲线变化的幅度很小，都在3.411左右小范围的浮动。通过流量的趋势图界面，还可以看出流量的变化趋势，可以实现对流量控制系统的实时监控。

图11 实验主界面

图12 流量的趋势图界面

通过本次实验可以看出，该控制方法完全满足生产过程的要求，对于节能减排、减少能源消耗具有重大意义。

6 结 论

（1）通过对离心泵工作原理的分析，建立了砂浆泵节能调速控制系统的数学模型，并对控制系统进行了控制性能分析，结果表明控制系统稳定且能观能控。

（2）为砂浆泵设计了基于BP神经网络的智能控制算法并进行了计算机仿真，可以得出这种控制方法相对于传统的PID控制方法系统的控制性能有了很大的提高。基于BP神经网络的智能控制算法对于提高系统的控制质量有很好的效果。

（3）为了得到最佳的控制性能，对原系统进行了极点配置优化，得到了最佳的数学模型，通过实验验证，可以得出极点配置优化算法，在 Wincc flexble与Smart－700IE触摸屏相结合的实验平台上运行稳定，误差较小。由实验可知，砂浆泵的节能调速控制研究的方法完全可以满足工业上的要求。

［1］马小亮.大功率风机、泵的节能调速发展方向探讨［J］.电气传动，1999（1）：1－2

［2］马冰雪，乞昆钢.泵用交流电机调速方法及节能分析研究［J］.电气节能，2006（3）：1－3

［3］许光映.变频调速泵系统性能的仿真研究［J］.节能技术，2006（1）：20－22

［4］李香燕.变频调速节能装置在液氨泵上的应用［J］.电工电气，2013（8）：39－40

［5］Xiu Lei，Meng Ni，Dong Li，et al.Study on simulation of digital pump－control cylinder position control system［J］.Procedia Engineering，2011，16：729－736

［6］刘应诚.风机水泵调速运行节能原理及其调速装置的选择［J］.液压气动与密封，2010（11）：43－44

［7］Yang Zhao，Zhao Haibo，Fang Zheng.Modeling and dynamic control simulation of unitary gas engine heat pump［J］.Energy Conversion and Management，2007，48：3146－3153

［8］Zhao Tianyi，Zhang Jili，Ma Liangdong.On－line optimization control method based on extreme value analysis for parallel variable－frequency hydraulic pumps in central airconditioning systems［J］.Building and Environment，2012，47：330－338

［9］Zhenjun Ma，Shengwei Wang.Energy efficient control of variable speed pumps in complex building central air－conditioning systems［J］.Energyand Buildings，2009，41：197－205

［10］Clara Verhelst，Filip Logist，Jan Van Impeb，et al.Study of the optimal control problem formulation for modulating air－to－water heat pumps connected to a residential floor heating system［J］.Energy and Buildings，2012，45：43－53

［11］房海蓉，方跃法.基于神经网络的机器人智能控制［J］.机器人技术与应用，2002（4）：28－31

［12］稽春燕，刘聪.基于BP神经网络的深水自升式海洋平台智能控制模型控制研究［J］.海洋工程，2013（2）：20－23

［13］罗勇武，周剑，黎勉，等.液压变频调速系统数学模型分析［J］.现代制造工程，2001（11）：1－5

［14］张艳玲，王耀南，薛殿伦.模糊自适应PID控制器在CVT速比控制中的应用［J］.自动化技术与应用，2005（2）：3－10 （责任编辑：汪材印）