一维势能图像能告诉我们什么？

周 佳 翁亚静

（江苏省常熟中学，江苏 常熟 215500）

所谓一维势能图像，它反映的是在一维情况下物体势能与空间的位置变化关系.例如重力势能与高度、弹簧振子的弹性势能与距平衡位置的位移、分子势能与原子间距等图像均属于一维势能图像.一维势能图像在物理学中有非常广泛的应用，它不仅可以直观地呈现出势能与位置的关系，而且可以反映出很多其他问题.

1 重力势能的一维势能图像

以竖直上抛运动为例，如图1所示，质量为m的小球，从地面上以Ek0的初动能竖直抛出，若规定地面为零势能面，则小球的重力势能与距地面高度h的关系满足

其一维势能图像如图2所示

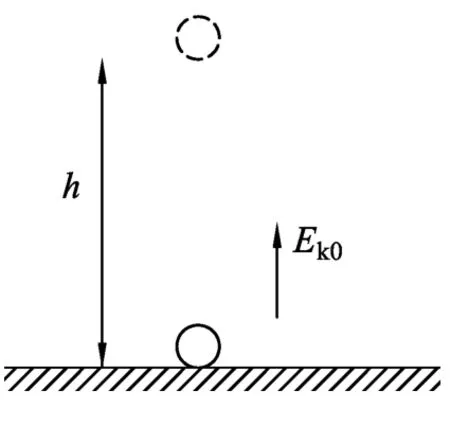
图1

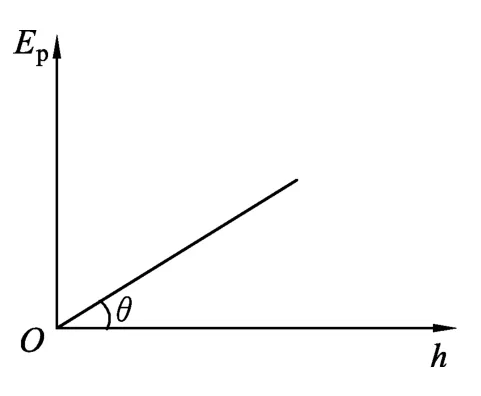
图2

下面我们通过重力势能的一维势能图像来讨论小球的作用力、能量等几个问题.

（1）作用力.由（1）式可知，图像的斜率即表示重力的大小，满足mg＝tanθ，且在上升的过程中力的大小与方向均不变.

（2）能量.令小球的总能量即机械能为E，由于机械能守恒，因此在整个过程中小球的机械能是个定值，机械能的大小用水平虚线表示（如图3所示），由图可知，势能图像距虚线的竖直距离即该处小球动能的大小.当h＝0时，Ep＝0，Ek0＝E，即当抛出时，小球的动能等于小球的机械能.

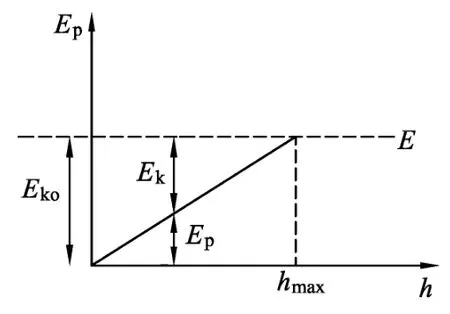
图3

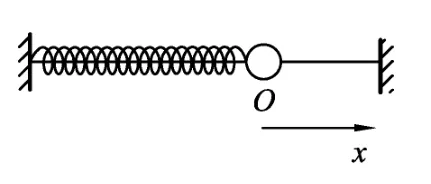
图4

（3）上升的最大高度.根据能量守恒定律，小球的重力势能不可能超过其机械能，因此图像与虚线的交点所对应的高度hmax，即为小球可以上升的最大高度，满足mghmax＝E＝Ek0.

2 弹性势能的一维势能图像

以水平弹簧振子（如图4所示）为例，弹簧的劲度系数为k，以平衡位置O为原点，则系统的弹性势能Ep与小球距原点的位移x满足的关系为

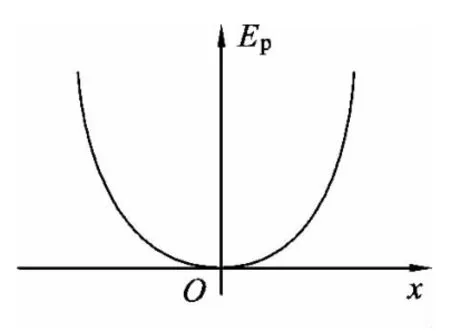
其一维势能图像如图5所示

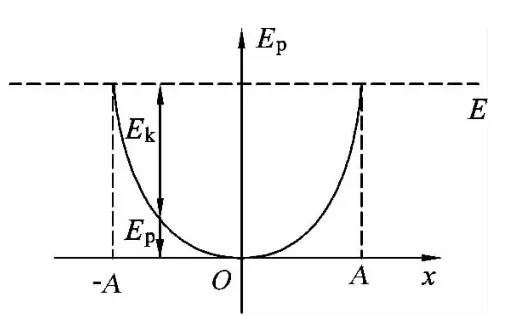
图6

接下来我们通过弹性势能图像来讨论弹簧振子的弹力、能量、振幅等几个问题

（1）弹力.由于势能曲线的斜率表示弹簧的弹力，因此由图像可知，在原点O处曲线的斜率为0即弹力为0，随着位移x的变大，曲线的斜率变大，故弹力变大.其次，由于弹力做正功，弹性势能减小，因此弹力总是指向势能减少的方向，即平衡位置O处.最后我们可以得到：弹簧弹力随位移的增大而增大，且方向始终指向平衡位置，这就是我们熟悉的回复力的特点.

（2）能量.令系统的总能量即机械能为E，由于系统机械能守恒，因此在整个过程中机械能是个定值，机械能的大小用水平虚线表示（如图6所示），弹性势能曲线距虚线的垂直距离即该处小球动能的大小.当小球的位移为零，即在平衡位置时，Ep＝0，Ek＝E，因此当小球经过平衡位置时，其动能最大.

（3）振幅.由于系统的弹性势能不可能超过其机械能，因此曲线与虚线的交点所对应的位移即为该弹簧振子的振幅A，满足

3 分子势能的一维势能曲线

原子之间的相互作用力叫做分子力，描写分子力的势能曲线如图7所示，其中横坐标代表两原子中心之间距离r，纵坐标是相互作用势能Ep（规定r→∞处的分子势能为0）.

（1）分子力.

① 当r＝r0时，由于势能曲线在该处的斜率为0，因此分子力为0.

② 当r＞r0时，由于分子力始终指向r0（平衡位置），故此时分子力体现为引力.并且随着原子间距的变大，曲线斜率先变大后变小，因此分子力先变大后变小.

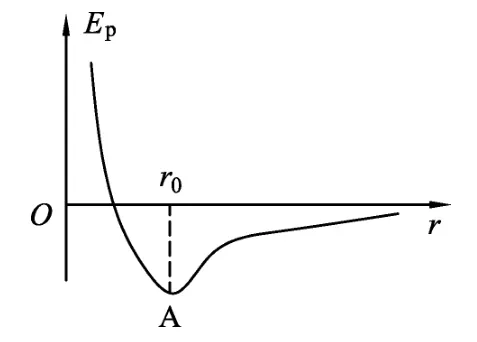
图7

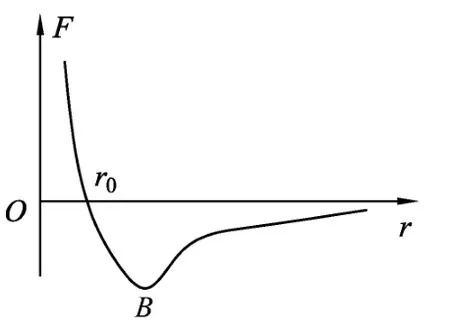
图8

③ 当r＜r0时，由于分子力始终指向r0（平衡位置），故此时分子力体现为斥力.并且随着原子间距的变小，曲线斜率变大，因此分子力变大.

由上面的讨论，可以得到分子力与原子间距的图像.（如图8所示）

图9

（2）势阱.如图9所示，在势能曲线的A处附近有一个低谷，通常称为“势阱”，由上面的讨论可知，A处的分子力为0.又因为A处附近的作用力都指向该位置，因此r＝r0是一个稳定的平衡位置.对于固体而言，其原子之间的距离就在r0附近，这也是为什么固体分子结构稳定的原因.

引入一维势能图像给了学生一个分析与解决问题的新角度，这不仅对学生深刻理解物理概念很有帮助，而且也锻炼了学生从多角度分析问题的能力.

1 赵凯华，罗蔚茵.力学［M］.北京：高等教育出版社，2011.