探寻物理量间定量关系的方法——对数法

潘学升

（高淳高级中学，江苏 南京 211300）

在探究物理规律时有时要具体探究物理量之间的定量关系，若物理量之间是线性关系或是反比关系只要先观察实验数据，后进行猜想和进行验证即可，整个过程并不复杂，但要是遇到复杂的定量关系，例如是二次方或是三次方关系或更复杂的关系，若仍采用先猜想后验证的方法，可能在寻找它们的规律时就会花费大量的时间，有时甚至无法找到所要的结果，很显然先猜想后验证的方法并不是最优的办法.如能通过对数据的处理先大致找到物理量之间的定量关系，再进行猜想与验证，这样处理就方便得多，利用数学中的对数就可以做到这一点，这种方法称之为对数法.下面就结合高中物理中遇到的较为复杂的定量关系来举例说明.

1 对数法处理数据的基本原理

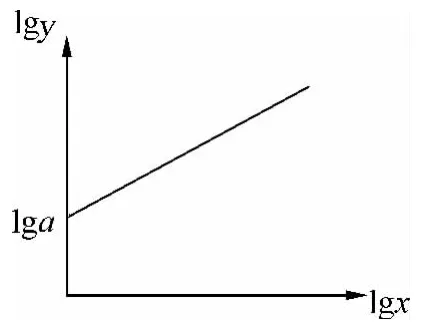
图1

当两个物理量不是成线性关系或反比关系时，我们可以根据条件先设一个函数，如y＝axb，a、b为常数，则lgy＝lga＋blgx，画出lgy－lgx的图像，如图1所示，则根据图像分析可知直线的斜率为b，截距为lga，其中a和b就是我们所要寻找的数值.

2 对数法在探究物理规律时的应用

2.1 对数法在探究单摆周期与摆长的定量关系的应用

表1是某学生在探究影响单摆周期与摆长关系时得到的数据，如表1所示，请根据数据找到T与L的定量关系.（注：数据来源于文献［1］）

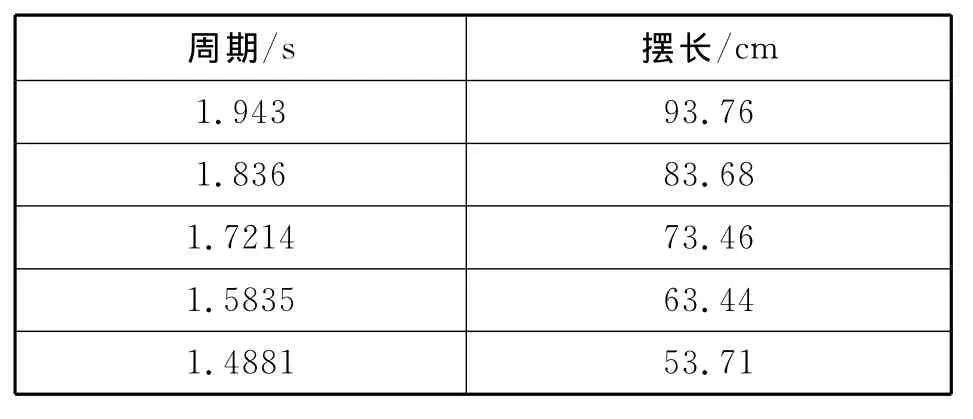
表1

分析：为便于处理，先把周期放大10倍，摆长放大100倍，然后取对数，得到表2.（注：在处理过程中不会影响log2T－log2L关系中的log2L前的系数，对数中是以2为底）

表2

画出log2T－log2L的关系图，如图2所示，从图像中可以得到斜率为0.4884，这与0.5非常接近，可猜测那么我们只要做出T2－L的图像，观察图像是否为过原点的一条直线，如果是就证明猜想正确.

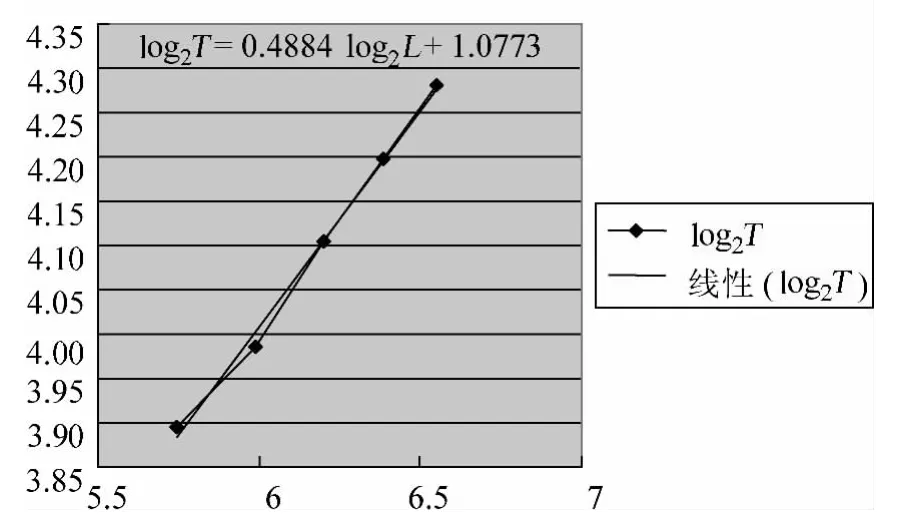
图2

先对表2数据进行处理，得到表3.根据表中数据绘制出T2－L的图像，如图3所示.

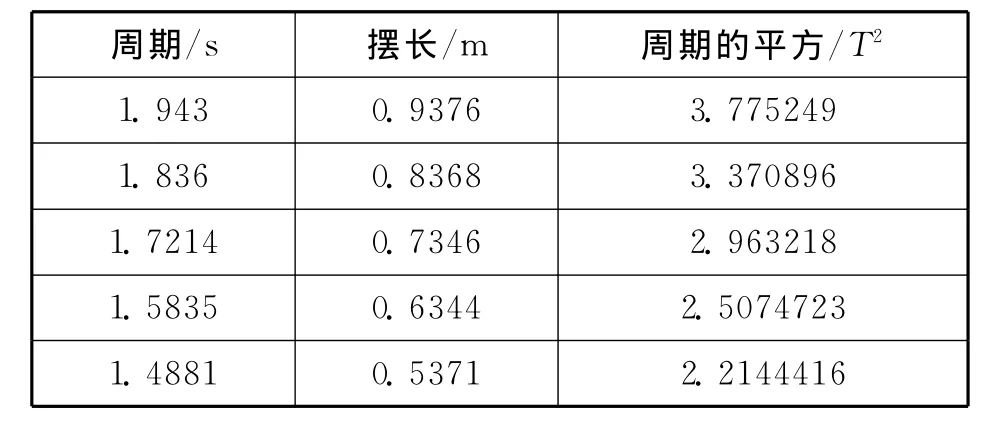
表3

从图3中我们发现T2－L图像是一条直线，从而证明猜想是正确的，也说明对数法在解决这类问题时是可行的.

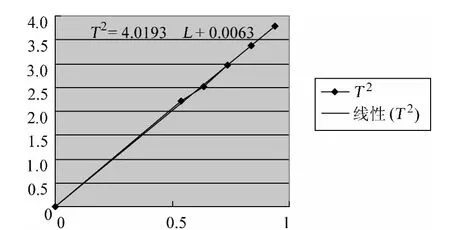
图3

2.2 对数法在探究行星运动周期与半长轴定量关系的应用

上述单摆周期与摆长的关系并不是特别复杂，高中阶段我们还学习过开普勒三大定律，其中第三定律的内容是周期与半长轴的关系，关系较为复杂，我们能否通过分析行星的运动规律来得到周期与半长轴的定量关系呢？不妨一试.

问题.如表4所示，这是当年第谷研究行星运动时的数据，请根据数据找到T与a的定量关系.

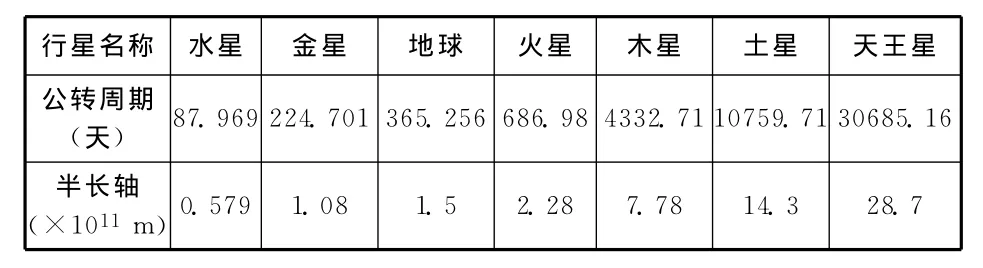
表4

分析：由于数据较大，故可以以水星数据作为参照处理，如表5.

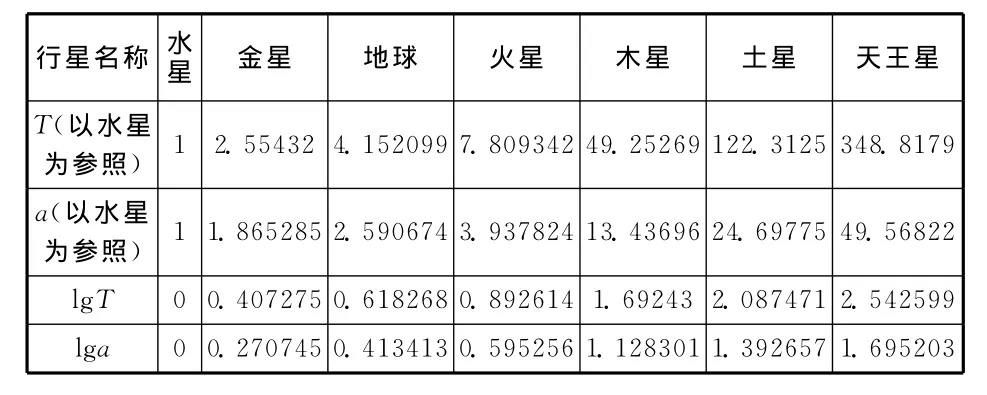
表5

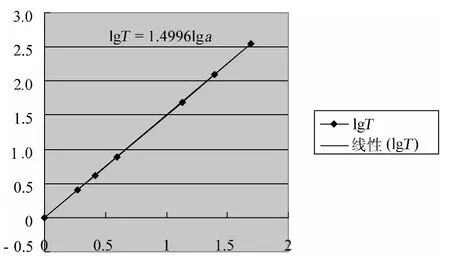
图4

根据表5的数据，利用Excel软件画出lgT－lga的图像，如图4所示，从中可以得到斜率为1.4996，这与1.5非常接近，我们可以猜想，猜想是否正确，只要画出T2－a3的图像，观察图像是不是过原点的一条直线，如果是就证明猜想正确.图5就是T2－a3的图像.（注：由于数据范围太大，我们做以下处理，T和R都以地球为参照，如表6所示，图像中参照的数据是水、金、地、火4大行星的数据）

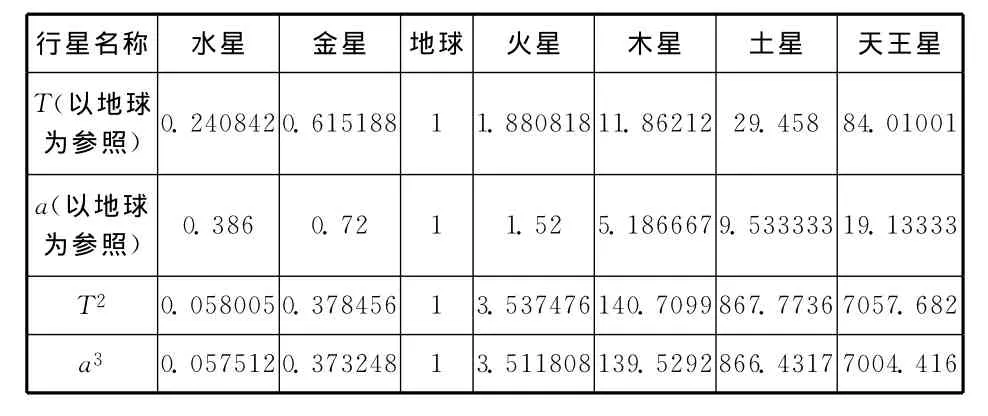
表6

从图5中可发现T2－a3图像是一条直线，从而证明猜想是正确的.

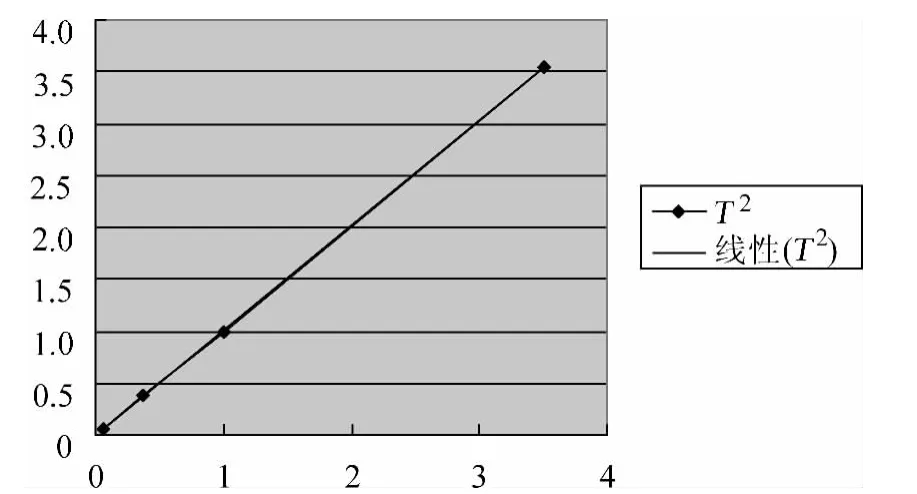
图5

3 方法总结

通过对两组实验数据的分析处理，我们发现利用对数法确实能够缩短猜想的过程，使得数据处理显得简洁明了.当然，由于高中阶段遇到的物理量之间的关系一般不是很复杂，所以，我们并不是常用到，但它不失为一种好方法.利用对数法处理数据能够使得物理量间呈现线性关系，故在求解物理量时也有其妙用，比如我们就可以用对数法处理单摆的实验数据，求解重力加速度等.由此可见，对数法在具体的应用中有着化难为易、化曲为直、化繁为简的作用，在高中物理实验教学中应渗透这种思想方法.

1 赵继红.单摆实验数据处理［J］.太原师范专科学校学报，2001（3）：12－13.

2 林彩钦.用图解法处理物理实验数据［J］.物理教师，2013（10）.