基于改进的K-Means算法入侵检测框架

李 蓉， 周维柏

(华南师范大学增城学院，广东广州 511363)

0 引言

现在网络攻击手段不断变化，导致网络入侵检测与防御机制需不断更新。由于正常流量与入侵流量常常容易混淆，致使入侵检测系统常发出大量的虚警，因此提升网络入侵检测系统的报警正确率是网络安全管理的一个非常重要的课题。

基于流量异常的检测的常用方法有:基于域值的检测方法、基于小波的检测方法、基于统计的检测方法、基于马尔可夫等随机过程模型的方法和一些基于机器学习、数据挖掘和神经网络等检测方法［1-6］，但这些方法主要存在报警意义不明确、可扩展性较差、协同运行差。

分类法主要是将网络流量分类，根据群聚特性，将发生频率稀少的流量类型定义为异常，分类技术有SVM、决策树、贝氏分类器等。但由于分群复杂度高，常造成难以在合理时间内得出最佳分群解，K-Means算法是一种最普遍也最广泛应用的分群技术［7-11］，但由于K-Means的目标函数不是凸面(Convex)函数，故可能包含许多区域最小值。近年来不少学者应用各种人工智能算法来求近似解，主要有基因算法、粒子分群算法及差分算法，三者都是以族群为基础的演变算法，比较不会受到初始解的选择而陷入区域最佳解的情况。但差分算法仍会因初始解的选择不好而造成执行时间过长的情况，依然有可能陷入区域最佳解。为解决此问题，本文算法结合K-Means算法和差分算法来找出最佳分群解;由K-Means快速分群求得局部最佳解，再利用差分算法求得全域最佳解，找出样本分群最佳群数，正确识别出正常行为和异常行为，实验表明此算法能快速有效地进行入侵检测。

1 K-Means算法

K-Means分群算法属于分割式算法。具体步骤如下:

Step1:随机选择k个样本作为初始聚类中心。

Step2:计算每个样本与各群群中心的距离。

Step3:根据Step2的结果将各样本分派给距离最近的群。

Step4:重新计算各群的群中心。

Step5:重复Step2至Step4，直到各群的群中心不再变动为止。

K-Means算法的优点是方法简单，可以快速获得解，但利用随机方式选取群组中心将影响算法的鲁棒性和正确性，而且必须预先要知道聚类个数k，各群的样本分布必须呈圆形分布，必须要有类似的大小时才可能得到最佳解，无法识别孤立样本。

因此本文结合密度、网格［12］和统计方法的概念，将初始群组中心这步骤独立出来，把算法规划为两个阶段来执行:①选取初始群组中心、识别孤立样本;②根据第一阶段的结果执行原始K-Means算法。具体步骤如下:

(1)阶段一。选取初始群组中心、识别孤立样本。

Step1:量化样本空间成为多个网格，并分配样本到所属的网格，同时计算各网格内样本的平均值。

Step2:计算所有网格样本量的平均值与标准差。

Step3:根据平均值与标准差标记出核心网格与孤立网格。

Step4:连结相邻的核心网格。

Step5:计算相连核心网格内样本的平均值，并将此平均值视为初始群组中心。

(2)阶段二。以第一阶段所选取的初始群组中心执行K-Means算法，孤立网格内的样本不纳入运算。

Step1:计算所有样本到各群组中心的距离。

Step2:分配各样本到距离最近(相似度最高)的群组。

Step3:计算各群组内样本的平均值，以决定新的群组中心。

Step4:重复以上3个步骤，直到各群的群中心不再变动为止。

2 差分算法

差分算法是一种以群体为基础来进行空间随机搜寻的最优化方法。算法过程如下:

(1)突变。随机选取 3 个向量 Xr1，G、Xr2，G、Xr3，G，通过突变因子F取得合成向量Vi，G+1。运算公式:

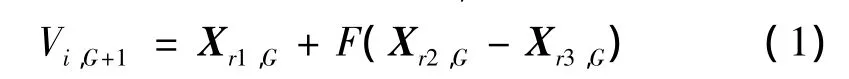
(2)重组。将合成向量与群体中所挑选出来的目标向量Xi，G，通过交配率CR的选择进行交配并产生试验向量。

(3)选择。通过适应值函数来评估目标向量和试验向量的适应值。选择适应值最好的一方进入下一世代，成为下一世代的目标向量。

3 本文算法

本研究主要是结合K-Means分群算法和差分算法，应用于网络入侵检测系统，使用分群技术将异常样本进行区分找出入侵行为。在算法开始前必须先将数据样本做前期处理，再运用K-Means分群算法调整群中心位置以寻找较佳群中心，接着执行差分算法，寻找出最适当的分群组数与分群结果。检测时利用样本与各群组间的距离来识别是属于异常或正常群组。算法流程图如图1所示。

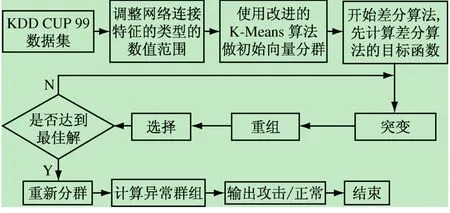
图1 本算法流程图

3.1 样本前期处理

本研究使用KDD CUP99数据集来评估此算法的识别效果。KDD CUP99数据集是由哥伦比亚大学IDS实验室整理形成的安全审计数据集［13-15］。数据类型分为连续和离散。将离散类型依其应用如ftp、http等按英文字母顺序的代号进行编号处理，转化为数字数据，连续属性的数字落差太大需采用正规化处理。本算法采用min-max正规化处理，公式如下:

其中:xi为第i个数据中连续的属性值;xmin为属性的最小值;xmax为属性的最大值为修正后的属性值。

3.2 利用K-Means算法作初始分群

大部分的分群技术都是计算连续数据，但K-Means算法也可以处理离散数据。系统一开始先调整离散数据和连续数据的数值范围，接着用K-Means算法调整群中心的位置寻找较佳群中心位置，让封包的样本更适合初始分群。

(1)进行分群。将所有样本分别指派到与群中心最近的位置。

先对每一笔样本，计算其归属于那一个群中心。连续数据的距离计算是由对每个样本到每个群中心的连续数据计算得到。而离散数据的每一样本到每个群心位置之间的距离的计算方式是离散数据在分群中出现的次数(最小的为1)，再除以分群样本总数。连续数据距离是运用欧几里德距离计算各样本点到群中心距离，并将其归类到最近距离的群。

(2)重新计算新的群中心位置。重新计算连续数据、离散数据的群中心位置。

根据上一步分群结果，重新计算各群的群中心位置，其中计算连续数据群中心位置，计算方式是求出每一个群各属性的平均值。而离散数据的群中心位置是重新计算各数据的支持度。计算方式是先计算子群的离散数据，和子群样本个数，统计出现次数最多的离散数据的出现次数，出现次数最多的离散数据值为数据的群中心位置。

3.3 结合DK算法找出分群结果

若未经K-Means算法作初始分群，会造成差分算法分群效果不佳。差分算法中，每个向量都是经由目标函数值评估后才得到保留适应值，封包信息所构成的每个向量都经由突变、交配及选择等运算，最后用选择评估适应值保留最佳的向量，再由循环执行的方式，来更新群中心位置，寻找出最佳的分群结果。

使用差分初始化分群的结果做突变机制，突变机制是在差分阶段找到的解向量中随机选取三个不同的解向量，彼此之间互相交叉运算，创造出一个新的向量，在此新的向量又称为差分向量，利用突变来调整初始群中心的位置，使用下式创造出差分向量;)其中为差分阶段找到的解向量中随机选取 3个不同的解向量;F为比例系数，介于0～1之间的数。若选取的向量比原来向量的适应度还差，经突变和交配，有机会寻找出更好的解。

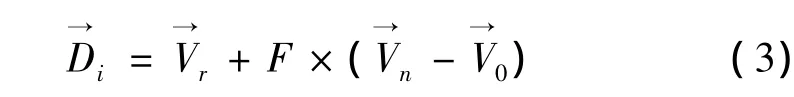
接着进行交配，产生不同的群中心的子代，使用下式产生新的子代解向量

再利用目标函数值计算交配后基因的适应度，去进行选择动作，使用下式做选择动作。

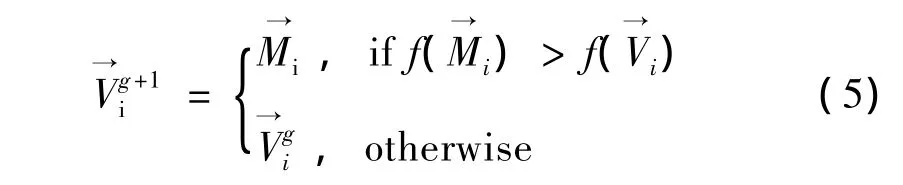
其中:为由突变、交配之后产生新的子代解向量为父代解向量;g为世代数。如此反复重新交配，更新最好的群中心位置，计算出差分算法后适应度最好的分群结果，而群内相异度低，表示分群的结果越好。

3.4 识别正常与异常群组

分群结果用来计算异常因子，计算群组之间的距离，来识别是属于异常或正常群组。使用组内平均距离的计算方式，计算方式主要是所有群组内资料与群中心的位置相加，之后除以分群组数，最后输出每群异常因子的结果，对群组的距离作排序，距离越大者为异常群组。

4 实验结果

实验使用的 KDD CUP99数据集分为 Normal、PROBE、DoS、U2R、R2L共5类网络攻击类型，训练和测试样本统计表如表1所示。

表1 训练和测试样本统计表

为了判断入侵检测的效果，采取两个重要的评估方法:检测正确率(DR)/误判率(FR)，

本算法不管初始解的好坏都可找到全域最佳解，因此本实验将群数值设定为30，比例系数设定为0.5，突变系数设为0.8，世代数设为2，解向量数设为5，并执行10次，去平均数。对比实验中K-Means算法的群数设为30，世代数设为500。

DoS攻击检测结果如表2所示，U2R攻击检测结果如表3，R2L攻击检测结果如表4，PROBE攻击检测结果如表5。误报率的统计结果如表6。各种网络入侵检测系统的检测率比较如表7。

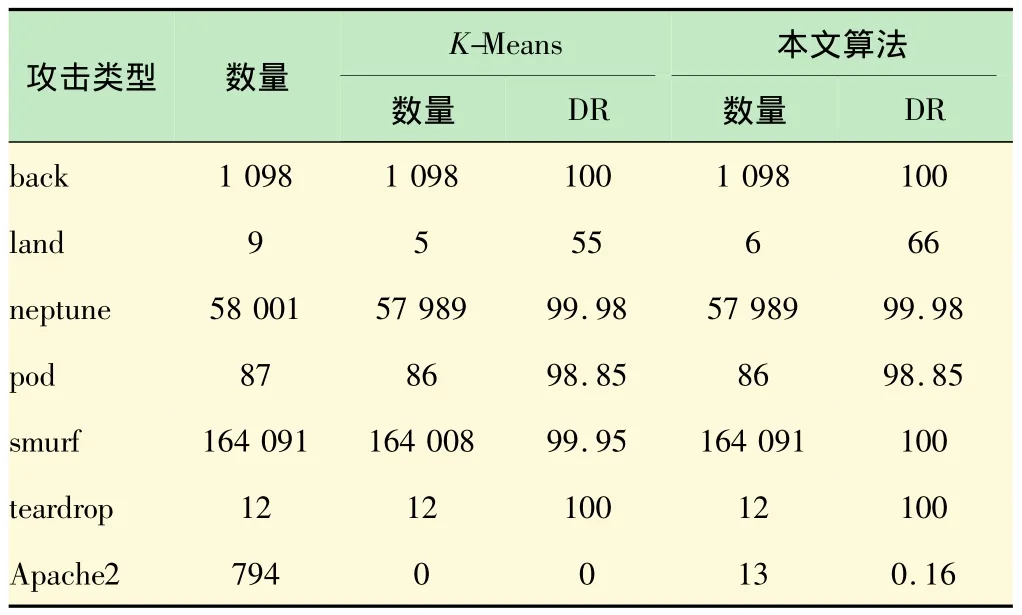
表2 DoS攻击检测结果

由表2可看出，在DoS攻击中，本算法对 back、smurf和 teardrop这三种攻击检测率为 100%，对apache2攻击本算法的检测率比K-Means高0.16%，对land攻击本算法的检测率比K-Means高11%，对smurf攻击本算法的检测率比K-Means高0.05%.

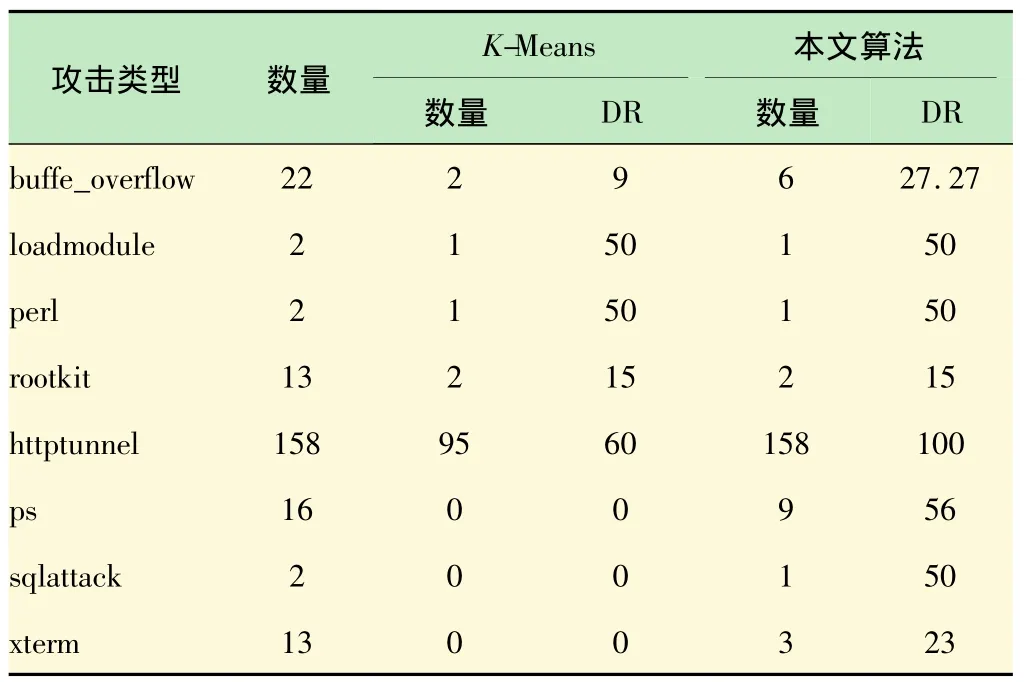
表3 U2R攻击检测结果

由表3可看出，在U2R攻击中，对buffer_overflow、httptunnel、ps、sqlattack、xterm 这 5 种攻击本算法的检测率比K-Means都要好。

表4 R2L攻击检测结果

由表4可看出，在R2L攻击中，对ftp_write、guess_passwd、imap、multihop、warezmaster这 5 种攻击本算法的检测率比K-Means基本都一样。但对phf攻击本算法的检测率比K-Means要高50%。由表5可看出，在PROBE攻击中，各种攻击本算法的检测率比K-Means都要好。由表2～6可看出，本算法在DoS、U2R、R2L、Probe各种攻击类型的检测能力比K-Means算法要好，提高了分群的准确率，改善K-Means算法的误判率，达到降低误判率的效果。

表5 Probe攻击检测结果

表6 误报率的统计结果

表7 各种网络入侵检测系统的检测率比较

5 结语

随着互联网的迅速发现，各种应用程序的蓬勃发展伴随着更多的安全漏洞，以及网络恶意行为已发展为庞大的地下经济行为，现在攻击手段更新快，这就要求检测技术也需不断更新。本文结合多种分类算法的方式进行分类，由K-Means快速分群求得局部最佳解，再利用差分算法求得全域最佳解。实验结果显示此改进方法对入侵检测有较好的效果。

［1］毛伊敏，杨路明，陈志刚，等.基于数据流挖掘技术的入侵检测模型与算法［J］.中南大学学报(自然科学版)，2011，42(9):2720-2728.

MAO Yi-min，YANG Lu-ming，CHEN Zhi-gang，et al.An intrusion detection model based on data mining over data［J］.Journal of Central South University(Science and Technology)，2011，42(9):2720-2728.

［2］刘衍珩，田大新，余雪岗，等.基于分布式学习的大规模网络入侵检测算法［J］.软件学报，2008，19(4):993-1003.

LIU Yan-Heng，TIAN Da-Xin，YU Xue-Gang，et al.Large-Scale Network Intrusion Detection Algorithm Based on Distributed Learning［J］.Journal of Software，2008，19(4):993-1003.

［3］易晓梅，陈波，蔡家楣.入侵检测的进化神经网络研究［J］.计算机工程，2009，35(2):208-209，213.

YI Xiao-mei，CHEN Bo，CAI Jia-mei.Research on Evolutionary Neural Network of Intrusion Detection［J］.Computer Engineering，2009，35(2):208-209，213.

［4］努尔布力，柴胜，李红炜，等.一种基于Choquet模糊积分的入侵检测警报关联方法［J］.电子学报，2011，39(12):2741-2747.

Nurbol，CHAI Sheng，LI Hong-wei，et al.Intrusion Detection Alert Correlation Based on Choquet Fuzzy Integral［J］.Acta Electronica Sinica，2011，39(12):2741-2747.

［5］杨雅辉，杜克明.全网异常流量簇的检测与确定机制［J］.计算机研究与发展，2009，64(11):1847-1853.

YANG Ya-hui，DU Ke-ming.Identification of Anomalous Traffic Clusters for Network-Wide Anomaly Analysis［J］.Journal of Computer Research and Development，2009，64(11):1847-1853.

［6］程国振，程东年，俞定玖.基于多尺度低秩模型的网络异常流量检测方法［J］.通信学报，2012，33(1):182-190.

CHENG Guo-zhen，CHENG Dong-nian，YU Ding-jiu.Network traffic detection based on multi-resolution low rank model［J］.Journal on Communications，2012，33(1):182-190.

［7］冯 波，郝文宁，陈刚占，等.K-Means算法初始聚类中心选择的优化［J］.计算机工程与应用，2013，49(14):182-192.

FENG Bo，HAO Wen-ning，CHEN Gang，et al.Optimization to K-means initial cluster centers［J］. Computer Engineering and Applications，2013，49(14):182-185.

［8］於跃成，王建东，郑关胜，等.基于约束信息的并行K-Means算法［J］.东南大学学报(自然科学版)，2011，41(3):505-508.

YU Yue-cheng，WANG Jian-dong， ZHENG Guan-sheng，et al.Parallel K-Means Algorithm based on constrained information［J］.Journal of Southeast University(Natural Science Edition)，2011，41(3):505-508.

［9］李大字，钱丽，靳其兵，等.改进的全局K'-Mmeans算法及其在数据分类中的应用［J］.信息与控制2011，40(1):100-104.

LI Da-zi，QIAN Li，JIN Qi-bing，et al.Modified Global K'-Means Algorithm and Its Application to Data Clustering［J］.Information and Control，2011，40(1):100-104.

［10］黎银环，张 剑.改进的 K-Means算法在入侵检测中的应用［J］.计算机技术与发展，2013，23(1):165-168.

LI Yin-huan， ZHANG Jian.Application of Improved K-Means Clustering Algorithm in Intrusion Detection［J］. Computer Technology and Development，2013，23(1):165-168.

［11］傅 涛，孙亚民.基于PSO的K-Means算法及其在网络入侵检测中的应用［J］.计算机科学，2011，38(5):54-55.

FU Tao，SUN Ya-min.PSO-based K-Means Algorithm and its Application in Network Intrusion Detection System［J］.Computer Science，2011，38(5):54-55.

［12］任家东，孟丽丽，张冬梅.一种基于网格的改进的K-Means聚类算法［J］.计算机研究与发展，2009，46(l):453-458.

REN Jia-dong，MENG Li-li，ZHANG Dong-mei.An Improved KMeans Clustering Algorithm Based on Grid［J］.Journal of Computer Research and Development，2009，46(l):453-458.

［13］Hettich S，Bay S D.KDD cup 1999 data［EB/OL］.http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html，1999.

［14］张新有，曾华燊，贾 磊.入侵检测数据集KDD CUP99研究［J］.计算机工程与设计，2010，31(22):4809-4816.

ZHANG Xin-you，ZENG Hua-shen，JIA Lei.Research of intrusion detection system dataset-KDD CUP99［J］.Computer Engineering and Design，2010，31(22):4809-4816.

［15］谷保平，许孝元，郭红艳.基于粒子群优化的k均值算法在网络入侵检测中的应用［J］.计算机应用，2007，27(6):1368-1370.

GU Bao-ping，XU Xiao-yuan，GUO Hong-yan.Research of K-Means algorithm based on particle swarm optimization in network intrusion detection［J］.Computer Applications，2007，27(6):1368-1370.