谐波齿轮传动的含间隙机构的动力学分析

孙东阳，陈国平，王铁成

（南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

谐波齿轮传动的含间隙机构的动力学分析

孙东阳，陈国平，王铁成

（南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

在考虑谐波齿轮柔性的基础上，研究了谐波齿轮传动对间隙机构动力学特性的影响。首先，利用非线性弹簧阻尼模型建立了谐波齿轮传动的含间隙机构的接触碰撞动力学模型。然后，对含间隙曲柄滑块机构进行仿真分析，结果表明谐波齿轮传动和机械部件柔性对间隙碰撞都有缓冲效果，只是机械部件刚度较大时，部件柔性的缓冲效果不明显，而降低机械部件刚度又将导致机械部件在运动过程中产生大变形，影响其机械性能。为谐波齿轮传动在含间隙机构中的应用，提供了理论依据。

谐波齿轮传动；间隙；磨损；曲柄滑块机构

由于设计公差、加工和装配误差、磨损，机械系统的运动副中广泛的存在间隙。间隙会使机械系统发生冲击和碰撞，加剧运动副的磨损，产生噪声和振动，影响机械的工作性能，因此，含间隙机构的研究，引起了国内外众多学者的关注。Flores［1］对含间隙的平面多体系统进行了比较系统的研究，并且通过比较有无间隙的曲柄滑块机构的系统响应得到间隙对系统的影响。随后，Flores［2］对含间隙的多体系统进行了更深入的研究，在考虑油膜润滑效果的基础上，建立了混合纯挤压油膜润滑模型，并且建立了含间隙的球关节和空间转动关节模型。Machado［3］对几种基于Hertz碰撞模型建立的碰撞力模型进行了比较，以评价这几种模型的优缺点和适用范围。Zhao［4］讨论了间隙大小对空间机器人机构动力学性能的影响。郝雪清［5］对四杆机构进行了研究，以分析不同运动副材料对间隙机构动力学特性的影响。

以上研究都是建立在刚体假设的基础上，研究发现：随着间隙增大，间隙对机构动力学特性的影响将更加显著［6］。为了减小间隙对机构动力学特性的影响，需要将机构设计得比较柔软或引入缓冲器。Bauchau等［7－8］对含间隙的柔性多体系统进行了研究，可以发现：系统的柔性会对含间隙机构的动力学响应有明显的影响。

谐波齿轮传动以其体积小、重量轻、噪声小、精度高、速比高和抗冲击等优点，已经被广泛的应用于机器人关节中［9－10］。然而，谐波齿轮传动的含间隙机构的研究却未见相关报道。本文对谐波齿轮传动的含间隙机构进行了动力学建模，并且以曲柄滑块机构为研究对象，在分析过程中分别考虑了谐波齿轮传动和连杆柔性，以分析谐波齿轮传动和连杆柔性对间隙碰撞的缓冲效果。

1 谐波齿轮传动多体系统动力学建模

1.1 谐波齿轮传动建模

由于谐波齿轮传动的柔性部件在机械系统的运行过程中将表现出扭转弹性。因此，具有谐波齿轮传动的机械系统，在建模时需要将刚性关节考虑为柔性关节。Spong［14］首先建立了柔性关节模型，其在建模过程中，基于以下两点假设：

（1）电机转子关于转子转轴对称，因此，转子质心的速度与转子的转动相互独立。

（2）关节的柔性被描述成线性弹簧，其弹性系数由关节的柔性特征决定。

基于以上两点假设其将关节柔性等效为线性弹簧，得到全局线性反馈的柔性关节模型。如果弹簧刚度趋近无穷大，则可以退化为标准的刚性关节模型。由于谐波齿轮传动过程中存在能量损耗，因此，在用Spong模型进行建模时，需要引入阻尼器以描述能量耗散，如图1所示。

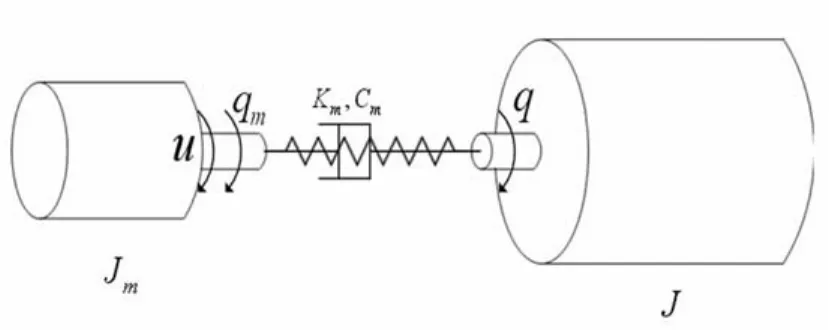
图1 单关节简化模型Fig．1 The simple model of single joint

具有n个自由度的柔性关节机器人模型表述为

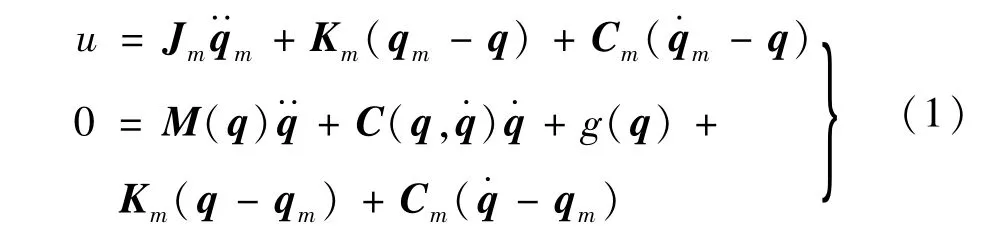
式中Jm、Km、Cm分别代表电机转动惯量矩阵、柔性关节等效弹簧刚度和等效阻尼；qm、q分别代表电机角度向量和关节角度向量；M（q）、M（q）、g（q）分别代表连杆转动惯量矩阵、离心力与哥氏力项矩阵和重力向量。

1.2 多体系统动力学建模

采用拉格朗日方法建立含约束的多体系统动力学方程为

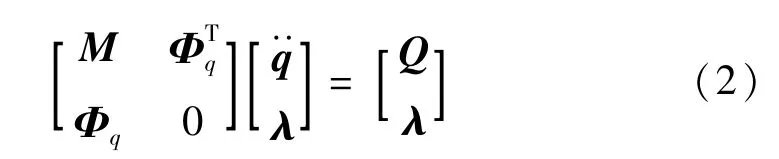
式中M为系统质量矩阵，Φq为约束方程对广义坐标的偏导数矩阵为加速度矢量，Q为系统广义外力，λ为拉格朗日乘子

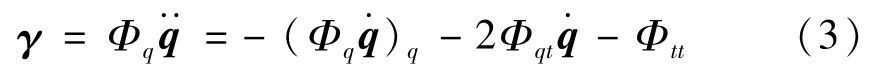
等式（2）是微分－代数方程，通过迭代可以得到每个时刻点的加速度。但是，等式中却不显含位移和速度约束方程，这将导致计算结果不能满足系统约束。为防止数值求解过程中违约，引入Baumgarte违约修正法［12］，则式（2）修改为

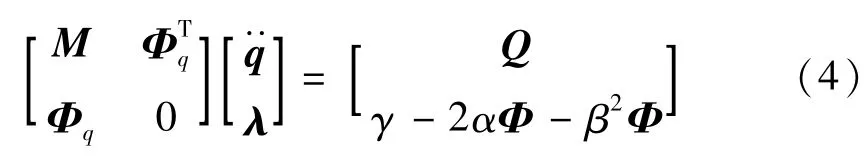
式中，α，β为稳定性系数

2 间隙铰接副建模

2.1 旋转铰间隙数学模型

由于磨损导致两个部件的连接不再是理想旋转铰，需要在旋转铰中引入间隙，同时将轴和轴承考虑为两个碰撞体［13］，如图2。在建模过程中，利用其力学关系将位移约束替换为力约束来建立间隙铰接副力学模型。

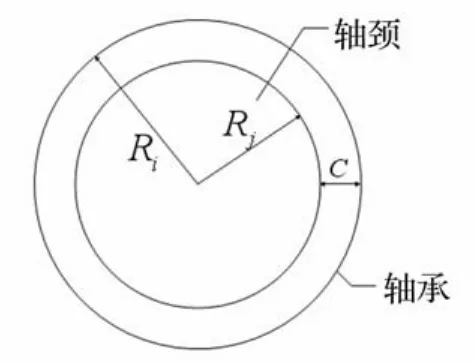
图2 含间隙的旋转铰模型Fig．2 Revolute clearance joint modeled as colliding bodies

注意单位向量n与轴和轴承中心连线有相同的方向。

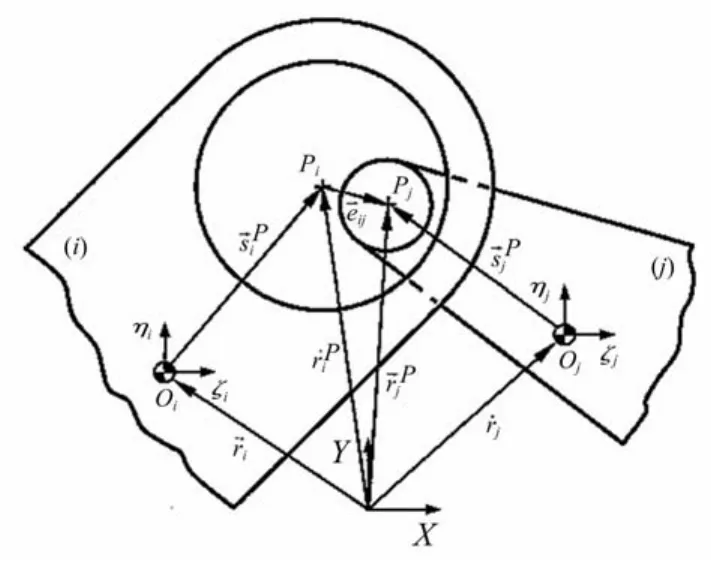
图3 多体系统中旋转铰间隙模型［13］Fig．3 General revolute clearance joint in a multibody system

如图4，当轴和轴承碰撞时，嵌入深度为

式中c为间隙大小其值等于轴承半径Ri与轴半径Rj之差。

于是，体i和体j的接触点Qi和Qj的全局位置为

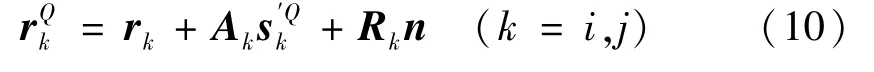
将式（10）对时间求导得到接触点Qi和Qj的全局速度矢量

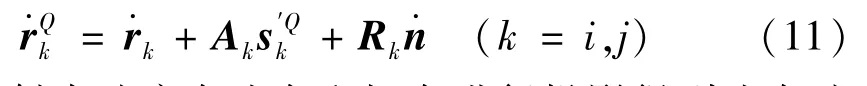
将接触点速度向法向和切向进行投影得到法向速度vN和切向速度vT为

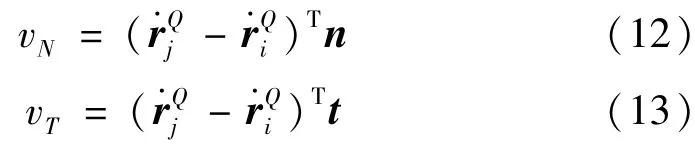
式中切向量t是通过向量n逆时针旋转90°得到。

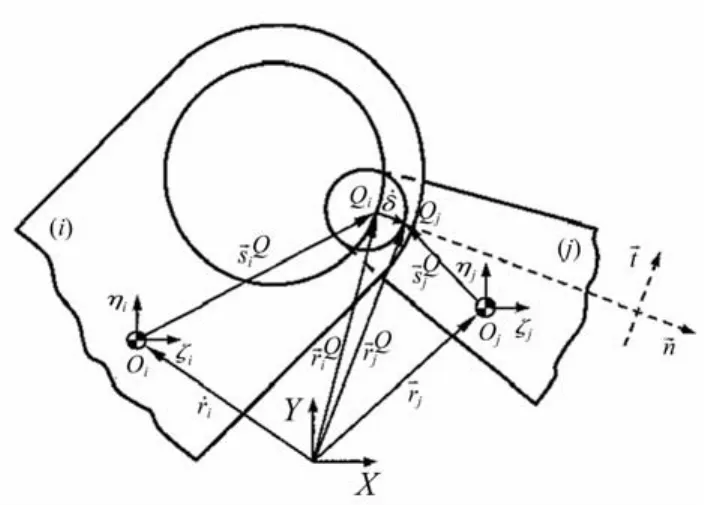
图4 轴和轴承碰撞时的穿透深度［13］Fig．4 Penetration depth due to the impact between the journal and the bearing

碰撞点处的法向力和切向力分别为fN和fT。将法向和切向接触力分别向X轴和Y轴投影，同时将接触力作用到体i和体j的质心Qi和Qj。如图5，作用在体i质心上的力和力矩分别为

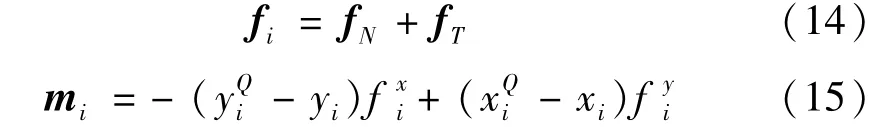
作用在体j质心上的力和力矩分别为

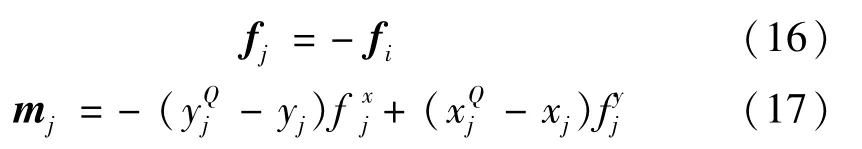
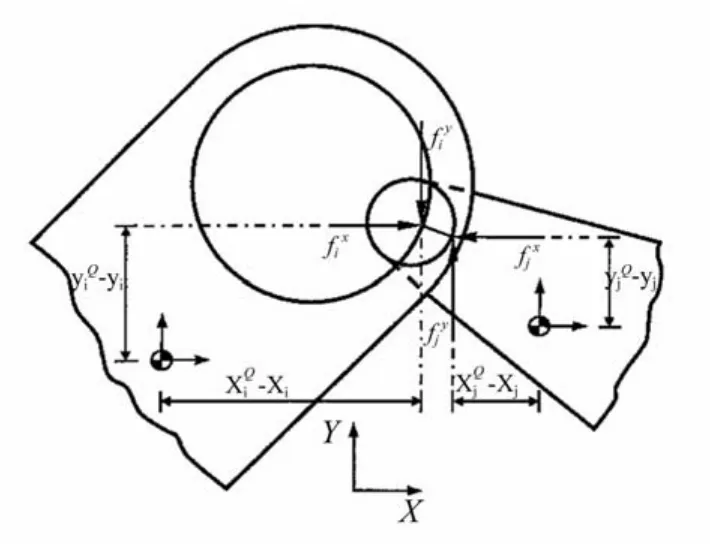
图5 碰撞点的力矢量［13］Fig．5 Force vectors that working at the points of contact

2.2 接触碰撞力模型

用于计算轴和轴承间碰撞力的接触碰撞力模型对存在间隙的机械系统的动力学仿真起着关键作用。接触碰撞力模型必须考虑接碰撞体的材料属性、几何特性、碰撞速度等信息。除此之外，模型还应该有利于机构动力学方程的稳定求解。研究者们认为，对于静态接触和低速碰撞情况，Hertz接触力模型比较适用。但是Hertz接触力模型不包含能量耗散项，因此不能描述接触碰撞过程中的能量损失行为。为了描述接触碰撞过程中的能量损耗，Hunt等［14］提出了非线性弹簧阻尼模型。随后，Lankarani等［15］在Hunt和Crossley的基础上，在Hertz接触模型中引入与恢复系数有关的虚阻尼项，提出了连续碰撞模型。这种碰撞力模型可以表示为

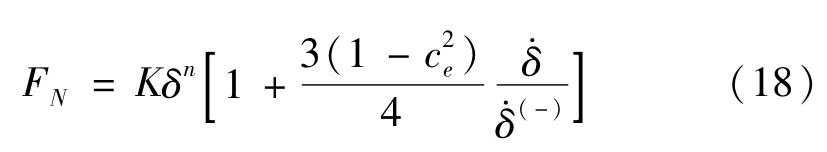
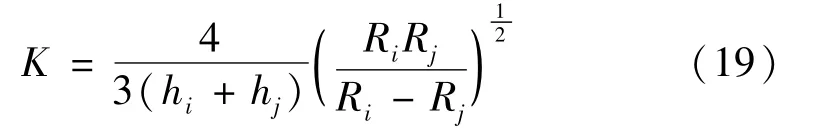
式中参数hi和hj为

式中vk为泊松比，Ek为弹性模量。

因此法向碰撞力为

3 算例：含间隙的曲柄滑块机构

本文以含间隙铰接副的曲柄滑块机构为研究对象，在分析过程中分别考虑了谐波齿轮传动和连杆柔性，以分析谐波齿轮传动和连杆柔性对间隙碰撞的缓冲作用。因此，本文基于三种情况对含间隙铰接副的曲柄滑块机构进行研究。首先对完全作刚性考虑的含间隙铰接副的曲柄滑块机构进行了研究。如图6所示曲柄滑块机构由地面1，曲柄，2，连杆3和滑块4组成。参考文献［2］，该机构的结构参数如表1所示，材料属性及动力学分析相关参数如表2所示。曲柄在驱动力作用下以5 000 r／min的恒定角速度运动。在初始情况下，曲柄和连杆都在水平位置，轴和轴承中心重合。

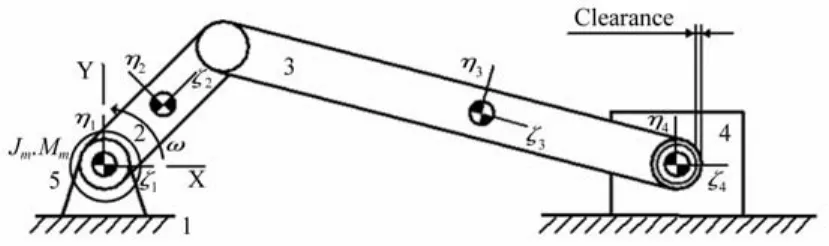
图6 含间隙的柔性关节曲柄滑块机构Fig．6 Flexible joint slider-crank mechanism with joint clearance

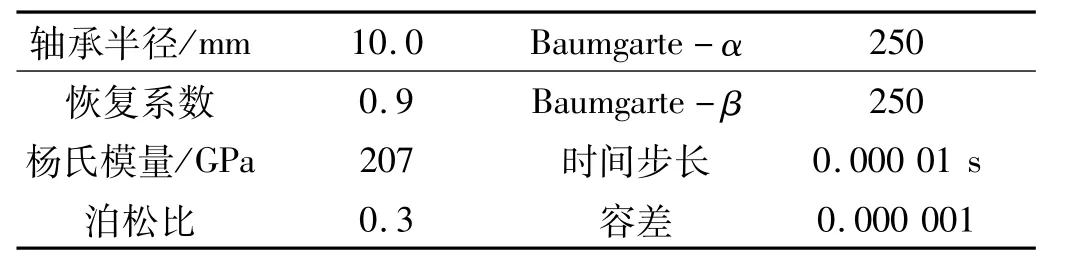
表2 曲柄滑块机构仿真参数Tab.2 Parameters used in the dynamic simulation of the slider-crank mechanism

随后，将连杆作为柔性体，用绝对节点坐标法［16－17］对其进行建模，将柔性连杆等分为4个单元，弹性模量为207 GPa，截面积为2．243 6×10－4m2，密度为7 800 kg／m3，截面惯量矩为4．194 7×10－9m4。间隙碰撞参数不变，以分析连杆柔性对响应的影响。

最后，对谐波齿轮传动的含间隙铰接副的曲柄滑块机构进行了研究。如图6所示，在上述模型的基础上增加了谐波齿轮传动5。本文基于Spong模型将谐波齿轮传动简化为线性弹簧－阻尼，驱动力作用于转子，使其以5 000 r／min的恒定角速度运动，再通过扭簧的变形带动曲柄一起运动。简化模型的等效扭簧刚度为2 000 Nm／rad，等效阻尼10 Nm／（rad·s），转子转动惯量0．000 005 kg·m2．分别取间隙c＝0．01 mm，c＝0．2 mm和c＝0．5 mm，其对应的接触刚度系数分别为1．52×107N·mm－3／2，3．42×106N·mm－3／2和2．20× 106N·mm－3／2。将上述三种间隙情况计算得到的响应结果与理想铰接副的响应结果进行比较。图7和图8分别为间隙c＝0．01 mm时，驱动力矩图和碰撞力图。由图7和图8可知：小间隙情况下三种间隙情况得到的驱动力矩和碰撞力与理想铰接情况的结果都比较接近，只是在考虑连杆柔性时，机构运动过程中，会激发出高频振动，导致驱动力矩图和碰撞力图出现很多毛刺。图9和图10分别为间隙c＝0．2 mm时，驱动力矩图和碰撞力图。图11和图12分别为间隙c＝0．5 mm时，驱动力矩图和碰撞力图。由图9－图12可知：当间隙变大时，间隙对系统响应有很明显的影响；当连杆刚度较大时，连杆柔性对间隙碰撞的缓冲效果不是很明显，反而会激发出柔性连杆的高频振动，使间隙碰撞更加频繁，从而使碰撞力和驱动力矩振荡比较剧烈；考虑关节柔性时，能够对间隙碰撞有很好的缓冲作用，并且能够抑制间隙碰撞中的高频振荡。

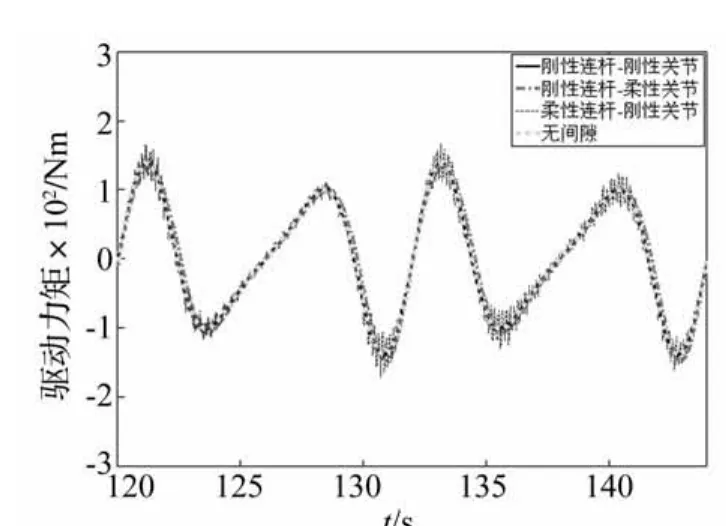
图7 理想和非理想铰接副驱动力矩（c＝0．01 mm）Fig．7 Comparison of driving moment between the ideal and the non-ideal joints with a 0．01 mm clearance

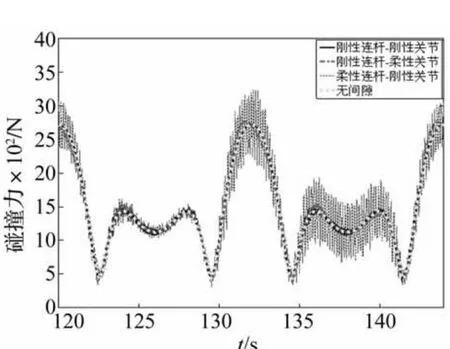
图8 理想和非理想铰接副间隙碰撞力（c＝0．01 mm）Fig．8 Comparison of contact force between the ideal and the non-ideal joints with a 0．01 mm clearance

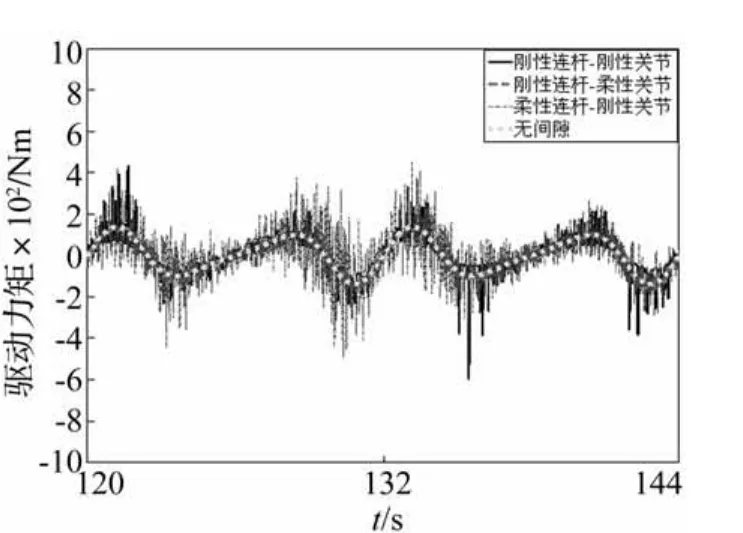
图9 理想和非理想铰接副驱动力矩（c＝0．2 mm）Fig．9 Comparison of driving moment between the ideal and the non-ideal joints with a 0．2 mm clearance

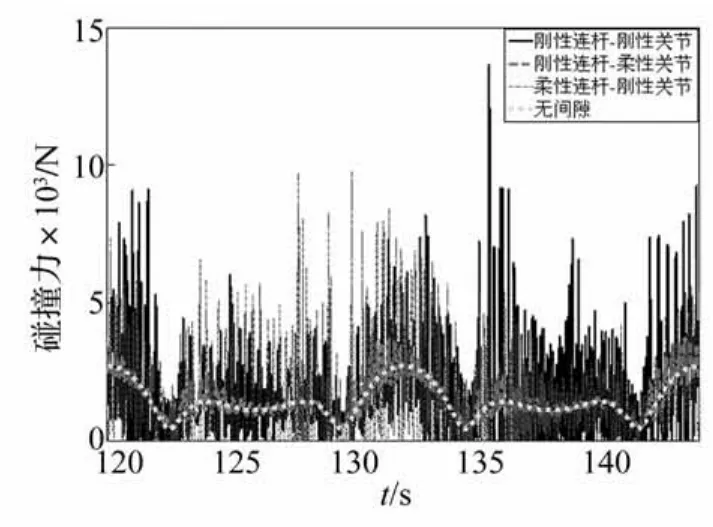
图10 理想和非理想铰接副间隙碰撞力（c＝0．2 mm）Fig．10 Comparison of contact force between the ideal and the non-ideal joints with a 0．2 mm clearance

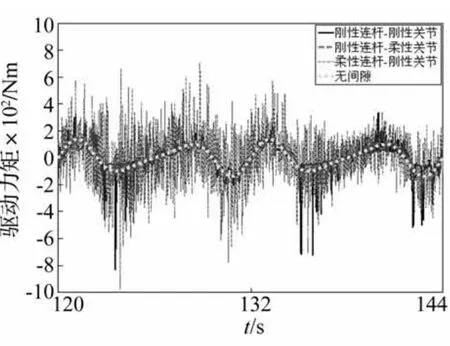
图11 理想和非理想铰接副驱动力矩（c＝0．5 mm）Fig．11 Comparison of driving moment between the ideal and the non-ideal joints with a 0．5 mm clearance

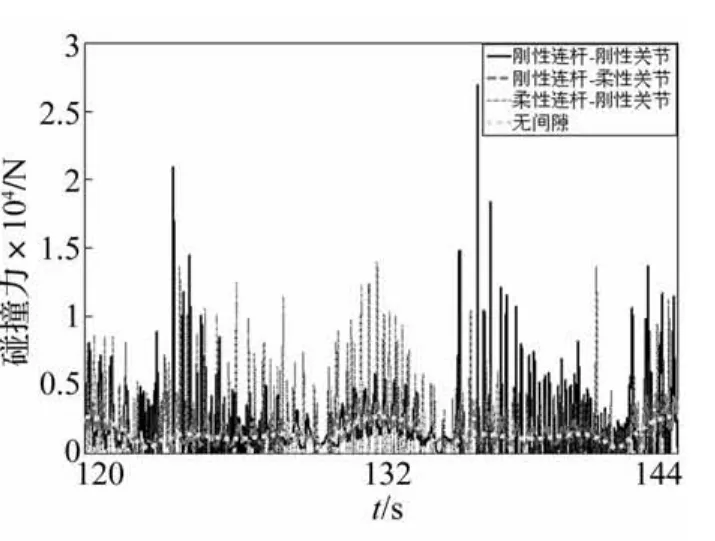
图12 理想和非理想铰接副间隙碰撞力（c＝0．5 mm）Fig．12 Comparison of contact force between the ideal and the non-ideal joints with a 0．5 mm clearance

为了研究连杆刚度下降时，连杆柔性对间隙碰撞的影响，在保持其它参数不变情况下，取连杆杨氏模量为2．07 GPa和20．7 GPa，分析间隙为0．5 mm的情况下三种间隙情况机构的驱动力矩和碰撞力，结果如图13和图14所示。

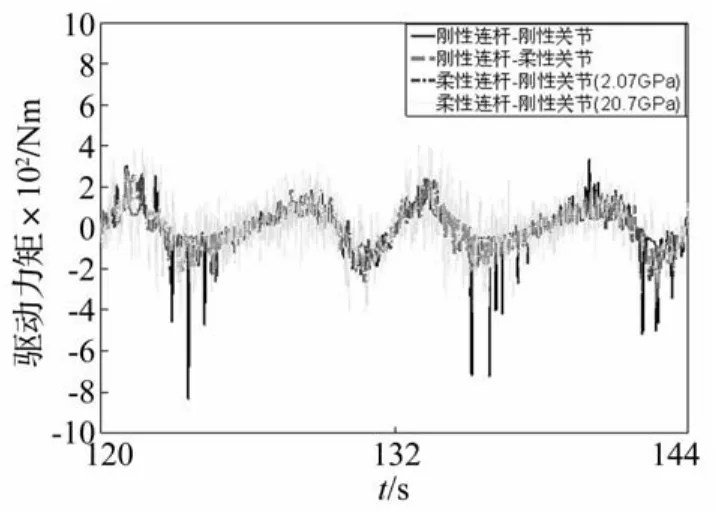
图13 非理想铰接副驱动力矩（c＝0．5 mm）Fig．13 Driving moment of non-ideal joints with a 0．5 mm clearance

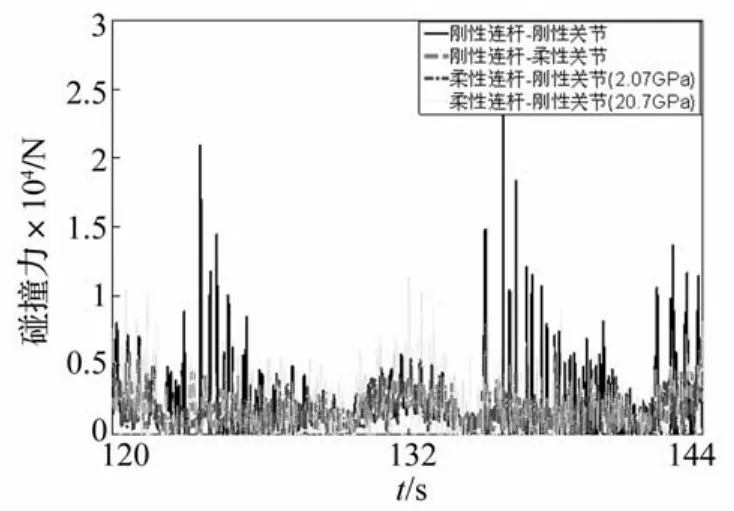
图14 非理想铰接副间隙碰撞力（c＝0．5 mm）Fig．14 Contact force of non-ideal joints with a 0．5 mm clearance

由图13和图14可知：当连杆刚度下降时，柔性连杆对间隙碰撞也有很好的缓冲效果。只是当连杆很柔软时，连杆在运动过程中将产生大变形，影响机构的机械性能，且不便于控制。

4 结 论

本文考虑到传统齿轮传动的含间隙机构碰撞比较剧烈，改用谐波齿轮传动以减缓间隙碰撞，提高机械性能。在建模过程中，考虑了谐波齿轮的柔性，建立了含间隙运动副的接触动力学模型。再通过对含间隙曲柄滑块机构进行分析，可以发现：谐波齿轮传动和连杆柔性对间隙碰撞都有一定的缓冲作用，只是连杆刚度较大时，连杆柔性的缓冲效果不是很明显，而降低连杆刚度又将导致连杆在运动过程中产生大变形，影响机构的机械性能。因此，在间隙机构中采用谐波齿轮传动，能够更好的改善机构的机械性能。

［1］Flores P，Ambrósio J．Revolute joints with clearance in multibody systems［J］．Computers＆Structures，2004，82：1359－1369．

［2］Flores P．Dynamic analysis of mechanical systems with imperfectkinematicjoints［D］．Guimaraes，Portugal：University of Minho，2004．

［3］Machado M，Moreira P，Flores P，et al．Compliant contact force models in multibody dynamics：Evolution of the Hertz contact theory［J］．Mechanism and Machine Theory，2012，53：99－121．

［4］Zhao Y，Bai Z F．Dynamics analysis of space robot manipulator with joint clearance［J］．Acta Astronautica，2011，68：1147－1155．

［5］郝雪清，陈江义．不同运动副材料对间隙机构动力学特性的影响［J］．振动与冲击，2012，31（12）：19－21．

HAO Xue-qing，CHEN Jiang-yi．Effects of different materials in joints on dynamic characteristics of a mechanism with clearance［J］．Journal of Vibration and Shock，2012，31 （12）：19－21．

［6］Muvengei O，Kihiu J，Ikua B．Numerical study of parametric effects on the dynamic response of planar multi-body systems with differently located frictionless revolute clearance joints ［J］．Mechanism and Machine Theory，2012，53：30－49．［7］Bauchau O A，Rodriguez J．Modeling of joints with clearance in flexible multibody systems［J］．International Journal of Solids and Structures，2002，39：41－63．

［8］Tian Q，Zhang Y，Chen L，et al．Simulation of planar flexible multibody systems with clearance and lubricated revolute joints［J］．Nonlinear Dynamics，2010，2010：489－511．

［9］熊根良．具有柔性关节的轻型机械臂控制系统研究［D］．哈尔滨：哈尔滨工业大学，2010．

［10］Saskatoon．Tiptrajectorytrackingofflexible-joint manipulators［D］．University of Saskatchewan，2009．

［11］Spong M W．Modelling and control of elastic joints robots ［J］．ASME Journal of Dynamic Systems，Measurement，and Control，1987，109（6）：310－319．

［12］Baumgarte J．Stabilization of constraints and integrals of motion in dynamical systems［J］．Computer Methods in Applied Mechanics and Engineering，1972，1（1）：1－16．

［13］Flores P，Ambrósio J，Claro J P．Dynamic analysis for planar multibody mechanical systems with lubricated joints［J］．Nonlinear Dynamics，2004，12：47－74．

［14］Hunt K H，Crossley F R．Coefficient of restitution interpreted asdampinginvibroimpact［J］．JournalofApplied Mechanics，1975，42：440－445．

［15］Lankarani H M．A contact force model with hysteresis damping for impact analysis of multibody systems［J］．Journal of Mechanical Design，1990，112：369－376．

［16］Omar MA，ShabanaAA．Atwo-dimensionalshear deformable beam for large rotation and deformation problems ［J］．Journal of Sound and Vibration，2001，243（3）：565 －576．

［17］García-Vallejo D，Mayo J，Escalona J L，et al．Efficient evaluation of the elastic forces and the Jacobian in the absolutenodalcoordinateformulation［J］．Nonlinear Dynamics，2004，35：313－329．

Dynamic analysis of a mechanism with clearances and harmonic gear transmission

SUN Dong-yang，CHEN Guo-ping，WANG Tie-cheng
（State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Here，the effects of harmonic gear transmission on dynamic characteristics of a mechanism with clearances，considering flexibility of harmonic gear were investigated．Firstly，the contact and impact dynamic model of a mechanism with clearances and harmonic gear transmission was established by using the nonlinear spring-damping model．Then，a slider-crank mechanism with clearances was simulated．The result showed that harmonic gear transmission and flexibility of mechanical parts have a cushioning effect on clearance impact；the cushioning effect is not obvious when the stiffness of mechanical parts is higher；while reducing stiffness of mechanical parts leads to larger deformation influencing the mechanical performances of the mechanism．The study results provided a theoretical foundation for the use of harmonic gear transmission in mechanisms with clearances．

harmonic gear transmission；clearance；wear；slider-crank mechanism

O313．7

A

10．13465／j．cnki．jvs．2014．23．029

江苏高校优势学科建设工程资助项目

2013－09－23 修改稿收到日期：2013－12－19

孙东阳男，博士生，1985年6月生

陈国平男，博士，教授，博士生导师，1956年生