参数慢变磁流变非线性悬架系统主共振研究

董小闵，王小龙，古晓科

（重庆大学机械传动国家重点实验室，重庆 400044）

参数慢变磁流变非线性悬架系统主共振研究

董小闵，王小龙，古晓科

（重庆大学机械传动国家重点实验室，重庆 400044）

针对磁流变阻尼器随工作温度变化导致阻尼力发生改变，进而降低磁流变悬架系统性能的问题，基于传热学方程和参数慢变非线性振动理论研究温度变化对磁流变非线性悬架系统的主共振动力学行为的影响。根据传热学理论建立磁流变阻尼器工作区域能量微分方程，用数值方法求出温度变化规律，用改进的Bingham模型计算磁流变阻尼力；建立慢变参数磁流变非线性悬架系统动力学方程，利用平均法求解主共振激励下的悬架动行程的稳态幅值响应。研究表明：随着运行时间增加，磁流变阻尼器的温度逐渐升高，导致磁流变阻尼力大幅降低，悬架动行程稳态振幅及其变化量越大，从而使得悬架系统的性能偏离设计目标。

慢变参数；磁流变阻尼器；温度；非线性振动

磁流变阻尼器作为一种智能阻尼器件，具有结构简单、响应快、能耗低、动态范围宽等优点，在结构振动控制领域受到了极大的关注。但近年来随着研究的深入，研究人员发现，磁流变阻尼器件会由于环境或自身原因导致温度的升高，引起输出阻尼力大幅降低［1］，导致系统动力学行为偏离设计目标，影响系统性能［1－2］。因此，有必要理解温度对系统动力学行为的影响规律，从而为不确定性悬架系统的优化和控制策略的调整提供研究基础。

温度引起磁流变阻尼器输出阻尼力的变化过程与控制周期相比，是一个缓慢变化的过程，磁流变振动系统属于参数慢变的非线性动力学系统，对其动力学行为的分析在理论上有一定的难度。目前国内外在温度对磁流变阻尼器的影响研究方面主要集中于磁流变阻尼器温升理论建模和控制补偿两个方面，而温度对于磁流变减振系统动力学行为影响方面的研究还很少。如Gordaninejad等［3］利用集总参数法建立了磁流变阻尼器温度的理论模型，实验验证该理论模型可以较好地预测温升。Liu等［4］研究了考虑温度补偿的1／4车辆悬架的天棚阻尼控制。Wilson等［5］针对一种远征战斗机（Expeditionary Fighting Vehicle）座椅，通过建立考虑温度变化的非线性Bingham模型（Nonlinear Bingham Plastic Model）提高了半主动天棚阻尼控制的鲁棒性。

目前慢变参数的非线性振动研究主要关注于系统质量和刚度发生缓慢变化时的解析方法，对于系统阻尼（如磁流变系统）缓慢发生变化的研究还比较少。如Kevorkian［6］的研究表明，如果不是选择恰当的快、慢尺度，传统的多时间尺度法失效。闻邦椿等［7］应用KBM法研究含有物料慢变参数的振动压实系统；陈予恕［8］应用KBM法研究具有任意个准循环坐标的多自由度系统的非定常解。李以农等［9］针对一类具有参数慢变的非线性振动系统，讨论了慢变系统的分析方法，结合转子系统的慢变刚度对其振动特性进行了研究。

为此，本文针对汽车磁流变悬架系统在运行过程中动力学行为随温度发生变化的问题，提出利用传热学和参数慢变非线性振动理论分析温度变化对汽车悬架系统动力学行为的影响。

1 温度影响下磁流变阻尼器输出阻尼力计算

磁流变阻尼器作为一种能量耗散装置，能将外界输入的振动能转换为自身的热力学能并耗散，该热力学能则表现为磁流变阻尼器在服役条件下的内部温升。Gordaninejad等［3］假设系统各组成部分在任意时刻具有相同的温度，利用集总参数法研究了磁流变阻尼器的温度随时间变化的规律。集总参数法是非稳态导热过程中物体的温度场的一种求解方法。在实际应用中，要求系统各点过余温度的最大偏差不超过5%，对应的特征毕奥数≤0．1。

假设液压筒内壁的温度与磁流变液的温度相同，利用集总参数法，建立磁流变阻尼器的能量微分方程

导出的热量以对流传热的方式传热到周围空气中，忽略热辐射传导方式，对流传热过程可表示为

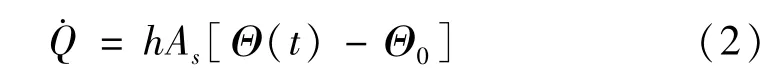
式中：h为液压筒壁和周围空气间的自然对流传热系数，As为阻尼器的外表面积，Θ0为阻尼器外围温度。

磁流变阻尼器中磁流变液的热力学能，由磁流变阻尼器做功和励磁线圈的电阻热组成。

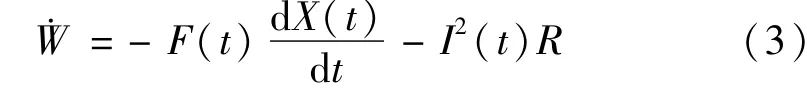
式中：F（t）为与温度有关的磁流变阻尼力，X（t）为随时间变化的位移激励，R、I分别为励磁线圈的电阻和加载的电流。

设激励为正弦激励，表示为

目前国内外学者在计算磁流变阻尼力时，考虑了温度变化因素的有非线性动态逆向模型（Nonlinear Dynamic Inverse Model，NLDIM）［2］、非线性加权双曲正切模型（Nonlinear Weighted Hyper-Tangent Model）［5］、温度唯象模型［10］、指数形式模型［4］和改进Herschel-Bulkley［11－12］等模型，但除了Herschel-Bulkley之外，其中绝大多数模型都不便于动力学方程的计算和分析。因此，本文利用Herschel-Bulkley模型计算考虑温度变化时的磁流变阻尼力。

Herschel-Bulkley本构关系模型为

为简化计算，取n＝1，Herschel-Bulkley模型即为改进的Bingham模型，从而得到磁流变阻尼力

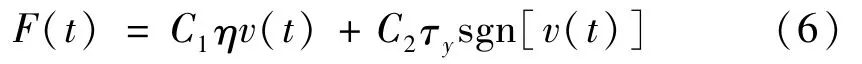
式中，C1和C2分别为与粘性阻尼和可控阻尼力相关的系数，由磁流变阻尼器的关键结构尺寸参数而定。

式（7）和式（8）可由数值方法联立求解，将式（9）代入式（7），即可求得阻尼力关于时间的表达式。

在得出磁流变阻尼力随温度的变化规律后，研究温度变化引起的阻尼力变化对主共振下汽车悬架系统动力学行为的影响。

2 慢变参数非线性汽车悬架系统主共振分析

结合第2节计算得到的磁流变阻尼力的表达式，以下研究如图1所示的主共振汽车磁流变悬架系统，建立动力学方程

式中：m为系统的质量，x和x分别为系统的垂直速度和加速度，x0为位移激励，k为刚度，F（τ）为温度慢变的磁流变阻尼力，由式（6）～式（9）确定，x（0）＝x （0）＝0

图1 单自由度汽车磁流变悬架系统Fig．1 SDOF vehicle MR suspension system

目前求解慢变参数动力学问题有效的方法主要有渐进法、多尺度法和平均法［7－9，13］。但渐进法只能用于求解激励力较小的动力学问题。多尺度法虽然可以用来求解较大激励力的动力学问题，但当动力学方程中有如可控Bingham力形式的静载荷时，不方便求解永年项。因此，本文选用平均法来求解。

在求得稳态响应幅值后，通过数值方法分析稳态响应幅值随时间的变化规律。

通过稳态振幅a对温度T求导数，可得到稳态振幅随温度的慢变规律，其表达式如下：

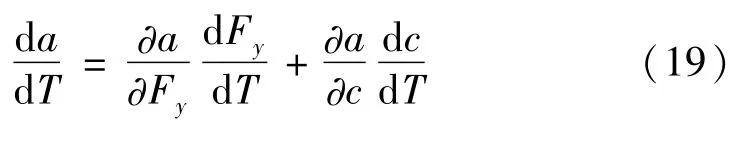
3 数值仿真

［3，15－16］，并结合实际的汽车磁流变悬架系统，选取仿真参数：As＝0．039 m2，R＝6 Ω，h＝2．5 W／m－2℃，λ＝0．000 85，m＝240 kg，k＝16 000 N／m，a＝0．003 8，c（0）＝1 100 Ns·m－1，b＝0．002 5。

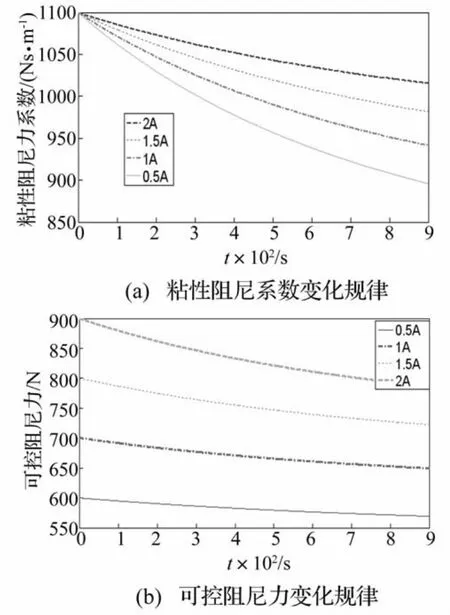
图3 磁流变阻尼力变化规律Fig．3 MR damping force-time history

图4为温度变化时悬架动行程的稳态振幅，加载电流分别为0．5 A、1．0 A、1．5 A和2．0 A。结合图2给出的磁流变阻尼器内部温度的变化规律，从图4中可以看出，随着运行时间增长，温度的升高，汽车磁流变悬架系统动行程稳态振幅变大，即温度的升高导致汽车磁流变悬架系统的隔振效果变差。此外，随着加载电流的增大，稳态振幅的最大变化量依次为1．1%、1．9%、3．2% 和4．6%，呈逐渐增大的趋势。

图5为不同加载电流下悬架动行程稳态振幅随慢变参数温度的灵敏度分析。结合图2和图4中给出的磁流变阻尼器内部温度变化规律和汽车磁流变悬架动行程稳态振幅随电流的变化规律，可以看出，随着电流的逐渐增大，磁流变阻尼器内部的温度升高的越快，汽车悬架系统动行程稳态振幅也逐渐增大，同时，稳态振幅对温度变化的灵敏程度也逐渐增大。

图4 汽车磁流变悬架动行程稳态振幅随电流的变化Fig．4 Steady-state amplitude of suspension stroke as a function of input electric current for MR damper

4 结 论

本文针对汽车磁流变悬架系统在运行过程中阻尼力随温度发生变化的问题，利用传热学和参数慢变非线性振动理论研究了非稳态温度慢变汽车磁流变悬架系统的主共振动力学行为。随着磁流变阻尼器运行时间增长，温度的逐渐升高，引起磁流变阻尼力大幅降低，导致悬架系统隔振性能偏离设计目标。此外，随着加载电流逐渐增大，磁流变阻尼器内部温度的升高越快，因此也导致悬架系统动行程稳态振幅的变化量也越大，稳态振幅对温度的灵敏度也越高，隔振性能逐渐变差。研究表明，为了充分发挥磁流变阻尼器的性能，在非稳态实时控制时需要进行合理的补偿，控制补偿的研究和实验验证将在后续工作中进一步进行。

图5 不同加载电流悬架动行程稳态振幅灵敏度分析Fig．5 Steady-state amplitude sensitivity analysis of suspension stroke as a function of input electric current for MR damper

参考文献

［1］Batterbee D，Sims N D．Temperature sensitive controller performance of MR Dampers［J］．Journal of Intelligent Material Systems and Structures，2008：1－13．

［2］Jumani S S．An invertible open-loop nonlinear dynamic temperature dependent MR damper model［D］．Master of Science In Mechanical Engineering，2010．

［3］Gordaninejad F，Breese D G．Heating of Magneto-rheological fluid dampers［J］．Journal of Intelligent Material Systems and Structures，1999，10（8）：634－645．

［4］Liu Y，Gordaninejad F，Evrensel C A，et al．Temperature dependent skyhook control of HMMWV suspension using a failsafe magneto-rheological damper［C］．Pro．SPIE 5054，SmartStructuresandMaterials2003：Industrialand Commercial Applications of Smart Structures Technologies，332，San Dieo，United States，2003．

［5］Wilson N L，Wereley N M，Choi Y T，et al．Performance robustnessofamagneto-rheologicalseatsuspensionto temperature variations using skyhook control［C］．Proc．SPIE 7288，Active and Passive Smart Structures and Intelligent Systems，San Dieo，United States，2009．

［6］Kevorkian J，Cole J D，Perturbation methods in applied Mathematics［M］．Springer New York，1981．

［7］辛丽丽，梁继辉，闻邦椿．考虑物料慢变参数的振动压实系统分析［J］．东北大学学报，2009，30（4）：585－588．

XIN Li-li，LIANG Ji-hui，WEN Bang-chun．Analysis of vibratingcompactorsysteminvolvingslowlyvarying parameters of compacted material［J］．Journal of Northeastern University：Natural Science，2009，30（4）：585－588．

［8］陈予恕．非线性振动［M］．天津：科学技术出版社，1983．

［9］李以农，郑玲，闻邦椿．一类具有参数慢变的非线性振动系统［J］．重庆大学学报，2000，23（6）：16－18．

LI Yi-nong，ZHENG Ling，WEN Bang-chun．Study on the nonlinear vibration system with slow-changing parameters［J］．Journal of Chongqing University：Natural Science Edition，2000，23（6）：16－18．

［10］徐赵东，李爱群，程文瀼，等．磁流变阻尼器带质量元素的温度唯象模型［J］．工程力学，2005，22（2）：144－148．

XU Zhao-dong，LI Ai-qun，CHENG Wen-rang，et al．A temperature phenomenological model with mass element of magneto-rheological damper［J］．Engineering Mechanics，2005，22（2）：144－148．

［11］Sahin H，Wang X J，Gordaninejad F．A new model for yield stress of magneto-rheological greases／gels under combined effects of magnetic field and temperature［J］．Proc．SPIE 7288，Active and Passive Smart Structures and Intelligent Systems，San Dieo，United States，2009．

［12］SahinH，WangXJ，GordaninejadF．Temperature Dependence of Magneto-rheological Materials［J］．Journal of Intelligent Material Systems and Structures，2009：1－8．

［13］闻邦椿，李以农，韩清凯．非线性振动理论中的解析解法及工程应用［M］．沈阳：东北大学出版社，2001．

［14］李韶华，杨绍普．采用改进Bingham模型的非线性汽车悬架的主共振［J］．振动与冲击，2006，25（4）：109－111．

LI Shao-hua，YANG Shao-pu．Primary resonance of a nonlinear vehicle suspension system using a modified Bingham model［J］．Journal of Vibration and Shock，2006，25（4）：109－111．

［15］郭树起．磁流变阻尼器动态特征分析及其在车辆悬架中的应用［D］．北京：北京交通大学，2005．

［16］王四棋，余淼，浮洁，等．正弦激励作用下磁流变阻尼器温升理论与试验研究［J］．机械工程学报，2013，49（8）：123 －128．

WANGSi-qi，YUMiao，FUJie，etal．Heatingof magnetorheological dampers under sine motion：theoretical andexperimentalstudy［J］．JournalofMechanical Engineering，2013，49（8）：123－128．

Main resonance analysis for a MR suspension system with slowly varying parameters

DONG Xiao-min，WANG Xiao-long，GU Xiao-ke
（State Key Laboratory of Mechanical Transmission，Chongqing University，Chongqing 400044，China）

The output damping force of a magneto-rheological（MR）damper is reduced with increase in working temperature．As a result，the performance of a MR suspension system is degraded．On the basis of the theory of heat transfer and nonlinear vibration，the main resonance of a MR suspension dynamic system with slowly varying parameters was analyzed here．The energy differential equations at the working area of the MR damper were established and solved with the numerical method．The modified Bingham model was applied to calculate the output damping force of the MR damper．The nonlinear dynamic equation of the MR suspension system with slowly varying parameters was formulated．The steady amplitude response of the MR suspension system under the excitation of main resonance was solved with the averaging method．The calculated results showed that the working temperature rises with increase in running time of the MR damper，consequently，the output damping force of the MR damper decreases significantly and the vibration amplitude variation of the suspension system increases，the performance of the MR suspension system is degraded．

slowly varying parameter；MR damper；temperature；nonlinear vibration

TH113．1

A

10．13465／j．cnki．jvs．2014．23．022

国家自然科学基金（51275539，60804018）；中央高校基金（CDJZR12110058，CDJZR13135553）

2013－09－12 修改稿收到日期：2013－12－19

董小闵男，博士，教授，1975年生