两端剪力薄膜支撑圆柱壳体的点导纳特性

杨明月，孙玲玲，王晓乐，高 阳

（山东大学高效洁净机械制造教育部重点实验室，济南 250061）

两端剪力薄膜支撑圆柱壳体的点导纳特性

杨明月，孙玲玲，王晓乐，高 阳

（山东大学高效洁净机械制造教育部重点实验室，济南 250061）

针对两端剪力薄膜支撑各向同性圆柱壳体的动力响应问题，基于多种经典薄壳理论及模态叠加原理，考虑到非径向振动惯性项的贡献，同时计入正余弦模态的响应，推导了圆柱壳体同时受简谐集中力与力矩激励下的力导纳、力矩导纳以及耦合导纳的完整解析表达式。算例表明，圆柱壳体运动方程中的非径向振动惯性项对各阶模态及导纳幅频的预估精度影响显著；耦合导纳实部具有可负性规律，对输入壳体的振动能量起着重要作用。旨在为两端剪力薄膜支撑圆柱壳体结构的减振降噪和以其为支承基础的主被动隔振系统的设计提供理论指导。

振动与波；圆柱壳体；模态分析；导纳；隔振

圆柱壳体结构以其良好的几何和力学性能在国防、工业及民用领域有着广泛应用。安装在圆柱壳体基础上动力装置产生的振动，不仅会影响其内机电设备的使用功能，还会以弹性波的形式在壳体中传播，同时辐射大量噪声，降低驾乘人员的舒适度抑或军事武器的隐蔽性和作战性能［1］。

导纳概念在研究线性系统受力、力矩等动态激励下的振动机理，定量分析传递到结构的振动能量中发挥了重要作用［2］。鉴于圆柱壳体运动方程及边界条件的繁杂性，对其导纳完整解析式的研究不多。而两端具有盖板的圆柱壳体因其适用范围广，振型函数简单，多数研究壳体导纳的文献均涉及此类边界条件（即简支，称剪力薄膜更准确［3］，缩写为SD）。Warburton［4］运用Goldenveizer-Novozhilov薄壳理论和模态叠加法，计算了SD-SD支撑圆柱壳体在径向集中简谐力作用下的稳态响应，但未给出力矩激励下的响应。Ming［5］采用Flügge-Byrne-Lur'ye壳体理论，推导了端部复杂激励下有限长圆柱壳体的低阶模态点导纳函数，并应用于端部耦合圆柱壳体的功率流传递特性研究。盛美萍等［6－8］对SD-SD支承加筋圆柱壳及板壳耦合结构的导纳特性进行了大量研究，不过较少探讨不同激励及响应组分之间的耦合导纳特性。郑继周［9］利用省略非径向（周向和轴向）振动惯性项的Donnell-Mushtari壳体方程，给出了复杂激励下SD-SD支撑圆柱壳体弯曲振动的点导纳解析解，因其未计入余弦模态响应组分，给出的点导纳表达式并不完整。

本文对两端剪力薄膜支撑各向同性圆柱壳体的点导纳进行了理论推导，考虑到非径向振动惯性项的贡献，同时计入正余弦模态的响应，给出完整的力、力矩以及耦合导纳解析表达式。结合算例探讨非径向振动惯性项对圆柱壳体各阶模态及导纳幅频的预估精度影响，分析耦合导纳实部的可负性规律。

1 圆柱壳体理论模态分析

采用柱坐标系来描述圆柱壳体运动，原点位于壳体左端圆心，各坐标轴及外施集中力、力矩方向（符合右手螺旋定则）如图1所示。为简化叙述，文中提到的力、力矩均指简谐力、简谐力矩。设圆柱壳体长度L，中面层半径R，厚度h，杨氏模量E，泊松比μ，体密度ρ。基于Kirchhoff-Love假设，并结合Hamilton原理给出圆柱壳体中面微元受分布力fx、fθ、fz和绕x，θ，z轴的分布力矩Tx、Tθ、Tz激励时的运动方程：

图1 圆柱壳体坐标系及外施载荷Fig．1 Cylindrical shell coordinates system and applied loads

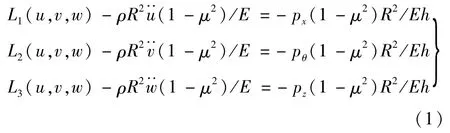
式中：u，v，w分别为壳体中面微元的轴向、周向和径向变形位移；L1（u，v，w）、L2（u，v，w）和L3（u，v，w）为相应的偏微分算子，其形式由所选用的薄壳理论确定。右端广义分布力项具体为：px＝fx－（∂Tz／∂θ）／2R，pθ＝fθ＋0．5（∂Tz／∂x）＋Tx／R，pz＝fz－∂Tθ／∂x＋（∂Tx／∂θ）／R

根据模态叠加原理，两端剪力薄膜支撑圆柱壳体的稳态响应平动及转动位移级数［10］可设为：

式中：Ψq（t）为圆柱壳体第q阶模态的参入因子；Uq（x，θ），Vq（x，θ），Wq（x，θ）分别表示壳体结构第q阶模态的轴向、周向、径向振型函数，共有两组（亦称奇偶模态或正余弦模态），相角差为π／（2n），对应相同的固有频率值。具体形式为：

式中：m为壳体振动轴向模态半波数，n为周向模态波数，两值的组合决定模态阶数q；Amni、Bmni和Cmni分别为第（m，n）阶模态的轴向、周向和径向幅值。

这里给出依据Goldenveizer-Novozhilov薄壳理论得出的结果。若采用其他薄壳理论，仅需重复上述步骤。

因为Amni、Bmni和Cmni存在非零解，故式（3）的系数行列式须为零，得频率方程：

由式（4）可以计算出圆柱壳体每阶模态的三个固有频率值。其中最小者对应壳体弯曲振动为主的固有频率［10］，另两者对应面内振动组分。为考虑壳体结构内阻，引入阻尼损耗因子η，将圆柱壳体有阻尼振动的固有频率表示为＝（1＋jη），下标i＝1，2，3代表三个固有频率组分。虽无法单独解出三个方向上的振幅分量Amni、Bmni和Cmni具体表达式，但由式（3）可得到两个振幅比：

2 圆柱壳体导纳函数推导

圆柱壳体结构更多的是承受面外载荷，而且线性系统的响应满足叠加原理，故当壳体上某点同时作用径向集中力Fz和绕x，θ两个坐标轴的集中力矩Mx、Mθ时，另一点的径向平动速度响应以及绕两个坐标轴的转动速度响应是所有激励引起的速度响应之和，写成矩阵形式：

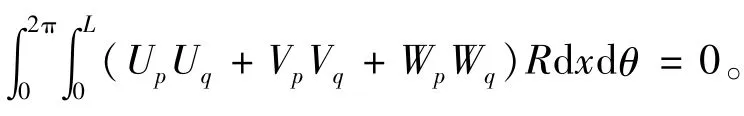
分布载荷可用集中载荷与Dirac Delta函数的乘积等效，故作用在壳体a点（xa，θa）的径向集中力Fz可以表述为：

将式（8）、（10）和（11）分别代入式（7）、（9），可以求出各阶模态参入因子Ψq（t），再把Ψq（t）代入式（2a，b）中，得到圆柱壳体b点（xb，θb）的稳态响应平动及转动位移表达式，最后根据导纳定义，将位移表达式对时间项exp（jωt）求导并除以相应的激励项，得出同时包含正余弦模态响应的圆柱壳体点导纳解析表达式：

需指出：式（12）～（20）中将面内振动组分（基频很高，对低频段导纳贡献甚微）一并计入，作为完整的导纳表达式；n＝0时对应圆柱壳体轴对称振动（亦称“呼吸振动”）模态情况；若激励点a与响应点b重合，式（6）便成驱动点（原点）导纳矩阵，为对称阵，满足线性系统互易性；由于圆柱壳体周向闭合，同一模态下，径向力（力矩）激励点处产生的转动速度（径向平动速度）相位差为π／（2n），叠加后相抵，故而四个驱动点耦合导纳（，，，）为零，并且圆柱壳体的驱动点导纳与周向坐标θ无关，只与轴向坐标x相关。

3 计算实例及结果分析

取结构钢制薄壁圆柱壳体进行计算，其几何尺寸和材料属性如下：L＝1 m，R＝0．25 m，h＝0．005 m，ρ＝7 850 kg／m3，E＝210 GPa，μ＝0．3，η＝0．002。

通常，工程上感兴趣的频带为0～1 000 Hz，由式（4）可得圆柱壳体面内振动（包含轴向与扭转振动）的基频为2 452．30 Hz，远超此频带范围。为确定圆柱壳体面外弯曲振动的各阶固有频率值，表1列出了文献［9］中频率公式（省略非径向惯性项的Donnell-Mushtari理论）和三种常用薄壳理论的计算值，并将其同商业有限元软件（ANSYS 12．0，shell63单元建模，2 000个元素，14 400个节点）分析结果的偏差百分比绘于图2。这里忽略有限元法模态分析固有的原理误差影响，从图2明显看出，基于文献［9］中频率公式的计算值相对偏差最大，而采用Goldenveizer-Novozhilov薄壳理论计算的结果相对精度最高。值得说明的是，对于长径比和厚径比越小的圆柱壳体，各理论计算精度差别越小［3］。因此，文献［9］中频率公式实际上更适合于短而薄（一般L／R≤2，h／R≤0．01）的圆柱壳结构固有频率计算。另外，三种常用薄壳理论所得各阶振型同FEA结果均相吻合，而利用文献［9］中频率公式所得振型，在第7、8、11～14阶（具体周向振型样式见图3，正弦模态对应振型只需顺时针旋转π／（2n）角即得）模态有较大出入，并在所关心频带范围内丢失了一阶模态。这表明，圆柱壳体的非径向振动惯性项对于各阶固有频率值及振型的预估精度影响显著，同时有必要选用适用性更广的Goldenveizer-Novozhilov薄壳理论确定壳体结构的固有频率及各阶振型。

表1 圆柱壳体弯曲振动固有频率（Hz）Tab.1 Natural frequencies of the flexure vibration of the circular cylindrical shell

图2 固有频率理论计算值同有限元分析值的偏差Fig．2 Deviations of the theoretical results compared with FEA

图3 圆柱壳体周向模态振型（余弦模态）Fig．3 Circumferential mode shapes（Cosine modes）

图4绘制了几种理论在力导纳幅值（跨点导纳情况下，激励点坐标为（0．6L，π），响应点坐标为（0．3L，π））上的差别。为尽量减少模态截断误差的影响，将圆柱壳体的120阶（m＝1～8，n＝0～14）模态计入导纳函数进行叠加。

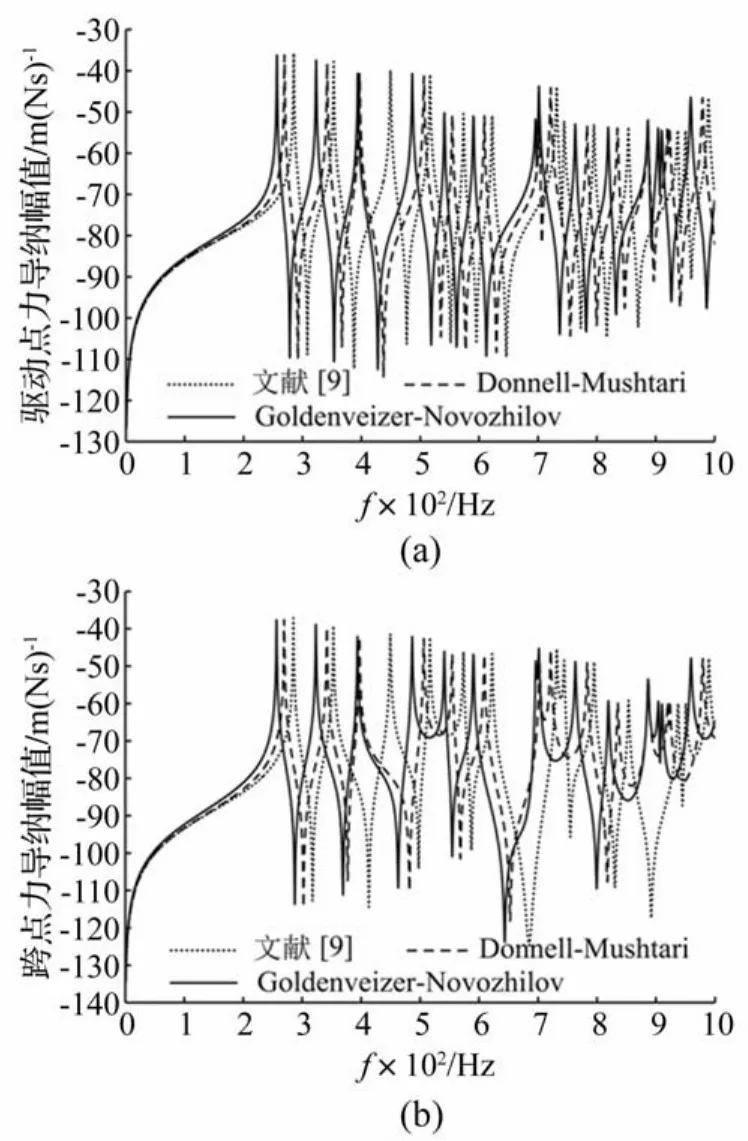
图4 力导纳函数幅值的比较（20log10Fig．4 Comparison of the magnitudes of force mobility functions

图5 导纳函数实部频谱（点线及点划线代表负值）Fig．5 Real parts of mobility functions（the dotted line and the chain line represent negative values）

据图4可知，无论在驱动点还是跨点导纳谱中，三条导纳线的各阶共振峰及反共振峰出现位置偏差均较大，但幅值大致相当。相较Donnell-Mushtari薄壳理论，文献［9］中省略了非径向振动惯性项，使得弹簧线下移而质量线上移，导致各阶固有频率值偏大。另外Donnell-Mushtari薄壳理论因省略了与面内位移相关的弯曲应变项及周向运动方程中的剪切项［10］，同Goldenveizer-Novozhilov薄壳理论相比，共振峰和反共振峰出现位置右偏。各力矩导纳及耦合导纳幅值的差别同样可得，限于篇幅，不再展开比较。综上表明，圆柱壳体的非径向振动惯性项对各阶模态及导纳幅频的预估精度影响显著，不能简单省略，同时鉴于实际工程中圆柱壳体结构尺寸的多样性，最终选定Goldenveizer-Novozhilov薄壳理论确定壳体结构的模态及导纳。

由于输入弹性结构的能量与其导纳实部之间存在着简单关系［2］，同时考虑激励点和响应点不同位置的影响，将导纳矩阵中各导纳元素的实部绘制成谱线，如图5所示。图5（a）～（c）中驱动点力导纳及力矩导纳实部均为正值，意味着当外部力、力矩作用于壳体结构时，壳体为能量接受体，力或力矩产生的振动能可直接输入到结构中。而图5（d）所示驱动点耦合导纳的实部中出现负值，表示壳体结构在特定频带上对外施载荷产生反作用，振动能量从结构流出。鉴于驱动点耦合导纳和均为零，这里讨论其轴向坐标x相同，周向坐标θ不同的跨点导纳情况。由图5 （e）、（f）可知，相应跨点耦合导纳实部中同样出现了负值。耦合导纳实部的这种可负性规律为壳体结构的减振降噪工作提供了一种潜在手段，可通过合理布置外施载荷的相对大小、位置来降低壳体结构在某个频率范围的振动功率。另外，从图5（a）～（c）中还可看出，当激励（响应）点位于L／2位置（即跨中）时，部分共振峰消失。由于壳体两端边界条件相同，这些未激发的模态取决于轴向节线参数m的取值情况。值得注意的是，从图5（d）、（f）中发现，当激励点位于壳体跨中处时，耦合导纳及的实部具有非常小量（10－25～10－15量纲之间），产生这种现象的原因在于圆柱壳体结构具有沿周向对称的边界条件（SD-SD），而位于跨中处的激励点正好满足轴向振型函数的对称条件。

4 结 论

基于多种经典薄壳振动理论，采用模态叠加原理，考虑圆柱壳体非径向振动惯性项的贡献，同时计及正余弦模态响应，推导出两端剪力薄膜支撑圆柱壳体在面外力和力矩激励下的点力导纳、力矩导纳和耦合导纳的完整解析表达式。

算例表明：两端剪力薄膜支撑圆柱壳体的非径向振动惯性项对各阶模态及导纳幅频的预估精度影响显著，不能简单省略。力导纳和力矩导纳的实部恒正，而耦合导纳的实部具有可负性，依赖于轴向节线参数m的取值以及激励与响应点的选取位置。耦合导纳实部的这种可负性规律为壳体结构的减振降噪工作提供了一种潜在手段。

所给出的点导纳推导过程及解析表达式，可方便拓展到线激励或加筋情况下，圆柱壳体的动力响应及声辐射研究；亦可结合子结构导纳法用于柔性圆柱壳体支承基础上的主被动隔振系统的设计。

［1］Hansen C H，Snyder S D，Qiu X J，et al．Active control of noise and vibration，second edition［M］．Boca Raton：CRC press，2012．

［2］Fahy F J，Gardonio P．Sound and structural vibration：radiation，transmission and response，second edition［M］．Oxford：Academic Press，2007．

［3］Leissa A E．Vibrations of shells（NASA SP－288）［M］．Washington D C：U．S．Government Printing Office，1973．

［4］Warburton G B．Harmonic response of cylindrical shells［J］．Journal ofEngineeringforIndustry-Transactionsofthe ASME，1974，96（3）：994－999．

［5］Ming R S，Pan J，Norton M P．The mobility functions and their applicationincalculatingpowerflowincoupled cylindrical shells［J］．Journal of the Acoustical Society of America，1999，150（3）：1702－1713．

［6］陈晓利，盛美萍．多加筋圆柱壳体振动特性的导纳法研究［J］．振动与冲击，2007，26（4）：133－135．

CHEN Xiao-li，SHENG Mei-ping．Vibrational characteristics of a multi-beam-stiffened cylindrical shell by mobility analysis ［J］．Journal of Vibration and Shock，2007，26（4）：133 －135．

［7］杨阳，盛美萍．加筋圆柱壳机械导纳分频段计算方法［J］．电声技术，2012，36（10）：58－62．

YANG Yang，SHENG Mei-ping．A new computing method for mobility of rib-stiffened cylindrical shell in different frequency bands［J］．Audio Engineering，2012，36（10）：58 －62．

［8］Zhao Zhi-mei，Sheng Mei-ping，Yang Yang．Vibration transmission of a cylindrical shell with an interior rectangular plate with the receptance method［J］．Advances in Acoustics and Vibration，2012，581769：1－9．

［9］郑继周，程林，张树生，等．复杂激励下有限长薄壁圆柱壳体导纳研究［J］．振动与冲击，2007，26（3）：120－123．

ZHENG Ji-zhou，CHENG Lin，ZHANG Shun-sheng，et al．Mobility of a finite long and thin cylindrical shell subjected to complex excitation［J］．Journal of Vibration and Shock，2007，26（3）：120－123．

［10］Soedel W．Vibrations of shells and plates，third edition［M］．New York：Marcel Dekker，Inc．，2005．

Point mobilities of circular cylindrical shells with both ends supported by shear diaphragms

YANG Ming-yue，SUN Ling-ling，WANG Xiao-le，GAO Yang
（Key Laboratory of High-efficiency and Clean Mechanical Manufacture，Ministry of Education，Shandong University，Jinan 250061，China）

Classical thin shell theories and modal superposition principle were used to investigate the dynamic response of isotropic circular cylindrical shells with both ends supported by shear diaphragms．The contribution of nonradial vibration terms and responses of their sinusoidal and cosine modes were taken into account．The force mobility，moment mobility and coupling mobility functions of a circular cylindrical shell simultaneously subjected to harmonic point force and moment excitations were derived．It was shown that non-radial vibration terms have remarkable effects on the prediction accuracy of amplitude frequencies of modes and mobilities，and the real parts of coupling mobility functions may be negative．The results provided a theoretical guidance for the vibration and noise reduction of cylindrical shell structures with both ends supported by shear diaphragms and for designing active and passive vibration isolation systems with these circular cylindrical shells as foundations．

vibration and wave；circular cylindrical shell；modal analysis；mobility；vibration isolation

TB535

A

10．13465／j．cnki．jvs．2014．23．018

国家自然科学基金（51174126）

2013－08－15 修改稿收到日期：2013－12－09

杨明月女，硕士生，1989年4月生

孙玲玲女，博士，教授，1967年12月生