考虑蜗孔尺寸的人耳耳蜗有限元模型研究

许立富，塔 娜，饶柱石，田佳彬

（上海交通大学振动、冲击噪声研究所机械系统与振动国家重点实验室，上海 20024）

考虑蜗孔尺寸的人耳耳蜗有限元模型研究

许立富，塔 娜，饶柱石，田佳彬

（上海交通大学振动、冲击噪声研究所机械系统与振动国家重点实验室，上海 20024）

建立人耳耳蜗的二维双向流固耦合有限元模型，包含卵圆窗、圆窗和基底膜等膜性结构，耳蜗管道中充满流体，采用流体－结构双向流固耦合动力学分析方法，在不同蜗孔尺寸时研究声音由卵圆窗传递到基底膜的机制。已有文献设置的蜗孔尺寸与人耳解剖文献中的蜗孔尺寸参数不一致，设置了三个不同蜗孔尺寸的耳蜗有限元模型，获得不同蜗孔尺寸对基底膜响应的影响，同时验证了耳蜗的频率选择特性，计算结果与报道的实验数据相一致。结果表明：设置合适的蜗孔尺寸，可以获得与实验数据更接近的结果。

耳蜗；蜗孔；基底膜；有限元模型；流固耦合

人的耳蜗是由充液管道以螺旋的形式盘绕2．5圈形成，耳蜗管道分为前庭阶、中阶、鼓阶三个腔体，耳蜗中重要的感音元件基底膜位于中阶，中阶底部的基底膜通过不同位置的振动感受不同频率的声音。

为了研究声音在耳蜗管道中的传递机制，已经提出了很多耳蜗的传声模型，其中包括数学模型［1－3］、有限元模型［4－9］和物理模型［10－11］。在数学模型中考虑基底膜与淋巴液之间的流固耦合作用相对比较困难，而物理模型是使用真实的结构去模拟耳蜗的响应，由于耳蜗结构比较复杂、尺寸相对较小，所以只能使用近似的结构进行定性分析。有限元模型在结构尺寸、材料属性上可以较好的模拟耳蜗的真实情况，利用专业的流体分析软件可以更方便地分析结构与流体之间的耦合作用。耳蜗有限元模型均将蜗管拉直以代替螺旋的蜗管结构，这是因为有文献表明螺旋的蜗管模型［12］计算的基底膜响应与拉直后的模型计算结果基本一致。

流固耦合方法根据流体与结构之间数据传递方式的不同可分为单向流固耦合与双向流固耦合。其中单向流固耦合是指流体场与结构场的微分方程单独求解，求解完成后再将流体场中的流体压力以载荷的方式加到流体与结构接触的结构表面，从而计算结构的变形。而双向流固耦合必须以瞬态计算的方式进行，在每一时间步都要完成流体与结构的数据传递。已有的耳蜗有限元模型，大多使用单向耦合计算耳蜗的响应，但实际耳蜗中的流体是不可压缩、有粘度的流体，并且基底膜的变形相对整个耳蜗的大小来说不能被忽略，基底膜的变形需要施加到流场中，所以本研究采用双向流固耦合方法来模拟耳蜗中流体与基底膜的相互作用。考虑到双向流固耦合计算的复杂性，本模型采用了简化的二维模型。

当前耳蜗的流固耦合模型把蜗孔面积设置为1 mm2左右［6，13］，但实际人耳蜗孔面积［14］为0．04－0．08 mm2，耳蜗尺寸对于耳蜗基底膜的响应特性有什么影响，至今没有相关方面的研究。所以，本研究考虑了三种不同的蜗孔尺寸，分析蜗孔大小对基底膜振动响应的影响。

本研究选择双向流固耦合方法，对耳蜗基底膜动力学响应特性进行仿真分析，建立了简化的耳蜗模型，包含卵圆窗、圆窗、基底膜等膜性结构，耳蜗内部充满流体；考虑不同的蜗孔尺寸，分析耳蜗在卵圆窗膜处激励时基底膜的响应，并对计算结果进行对比分析。

1 方法

1.1 几何模型和网格

在有限元分析软件ADINA中建立耳蜗的几何模型，包含结构部分和流体部分。真实的人耳蜗是由充液管道盘绕2圈半形成，蜗管分为前庭阶、鼓阶和中阶三个腔体，中阶有基底膜和柯蒂斯器，因为已经有很多的耳蜗力学研究包括数学模型、有限元模型和物理模型，均将蜗管简化为拉直的管道［15－16］。所以在本研究中，将蜗管简化成二维的长方形管道，被动的耳蜗模型忽略柯蒂斯器，把中阶简化为基底膜，从而位于管道中间的基底膜将充液管道分成两个腔体，分别是前庭阶和鼓阶，它们在耳蜗顶端的蜗孔处连通。

耳蜗基底膜长度约32 mm，宽度和厚度上都是线性变化的，宽度从基底端0．1 mm变化到顶端0．5 mm，厚度从基底端7．5 μm到顶端2．5 μm，根据文献［14］前庭阶和鼓阶容积分别为90和91 mm3，卵圆窗长和宽分别为1．5和3．4 mm，圆窗长和宽分别为2．25和1 mm。在ADINA软件中建立二维的结构几何和流体几何模型，结构模型包括基底膜和圆窗膜，流体模型包括卵圆窗、前庭阶和鼓阶，在基底膜顶端有蜗孔，见图1所示。简化后的耳蜗长32．2 mm，卵圆窗长1．2 mm，圆窗长1 mm，基底膜长32 mm。

图1 简化耳蜗模型Fig．1 Simplified cochlear model

结构模型中基底膜长32 mm，分成16段，每段长2 mm，圆窗几何长1 mm，将基底膜和圆窗划分成二维梁单元，单元尺寸0．05 mm，基底膜划分为640个单元，圆窗划分为20个单元。将基底膜的两个端点和圆窗的两个端点设置为固定约束，基底膜和圆窗均设置为流固耦合边界。

对流体模型划分网格，考虑到基底膜与流体的相互耦合作用，故流体网格会有变形，流体网格选择三角形单元，单元尺寸0．05 mm，共77 528个单元。卵圆窗处的输入边界设置为moving wall边界，输入固定幅值的正弦激励。基底膜和圆窗作为流固耦合边界，其余边界设置为wall。

1.2 材料属性

结构的材料属性设置包括弹性模量、密度、泊松比，为了模拟基底膜随着长度变化刚度变化的现象，给每段基底膜的材料赋予不同的属性，根据文献［17］的报道，基底膜的材料属性设置见表1所示，其弹性模量沿着耳蜗管道长度方向从底端到顶端逐渐减小，分布在20 MPa－95 MPa之间，密度设置为2 000 kg／m3，泊松比0．3。圆窗的弹性模量设置为3 MPa，密度设置为2 000 kg／m3，泊松比设置为0．3，阻尼系数为0．005。流体材料设置密度为1 000 kg／m3，粘度为0．001 Ns／m2，体积模为200 MPa。

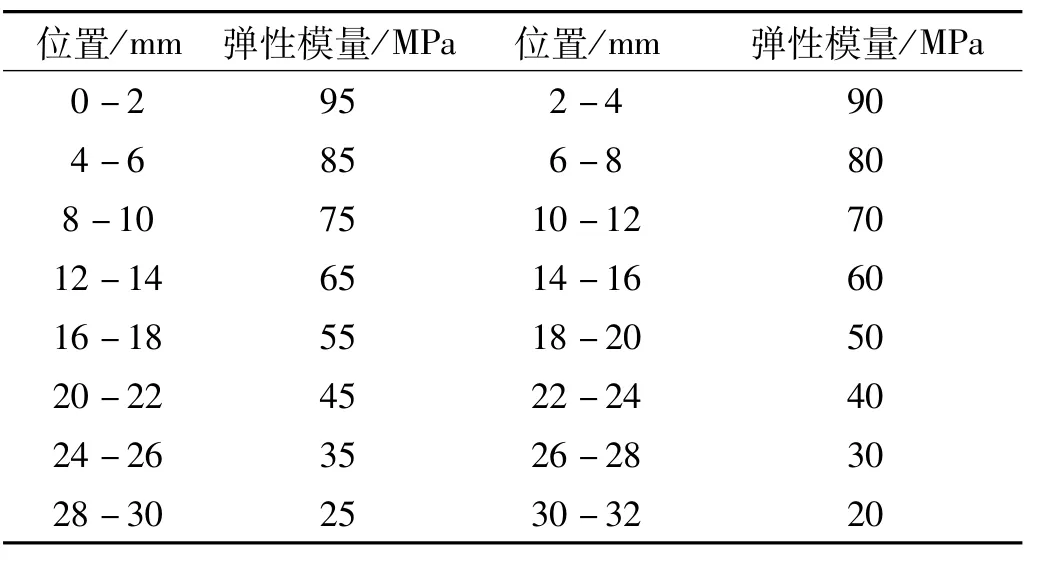
表1 有限元模型基底膜材料参数Tab.1 Basilar membrane material parameters of finite element model

1.3 蜗孔尺寸

参考已有有限元模型文献，Gan等［16］建立的耳蜗流固耦合模型均把耳蜗面积设置为1 mm2左右［6］，但人耳解剖文献中的真实的耳蜗蜗孔面积在0．04 mm2～0．08 mm2之间，已有有限元模型文献的设置与真实的耳蜗蜗孔尺寸相比较大，因此本文对不同的耳蜗尺寸进行模拟仿真。考虑到人耳蜗孔面积约为0．04～0．08 mm2，假设蜗孔为圆形，则其半径范围约为0．11～0．15 mm，简化到二维模型中蜗孔尺寸为直径值，故设置蜗孔尺寸0．2 mm。为了对比不同蜗孔尺寸下基底膜的响应，另建立蜗孔尺寸为0．5 mm和0．01 mm的耳蜗模型，一个比较大而另一个较小，分别计算这两个流固耦合模型，对其结果进行对比分析。

2 计算结果

2.1 0．2 mm蜗孔尺寸模型

卵圆窗处10 nm幅值正弦激励下基底膜的位移响应见图2所示，图2包含了100～10 kHz范围内的6个不同激励频率下基底膜的位移响应，描述了基底膜的位移幅值沿着长度方向的分布情况。图2（a）用对数坐标形式表示基底膜的振动位移幅值，图2（b）是对卵圆窗位移做规范化处理后的基底膜位移（dB）。如图2（a）所示，基底膜的最大振幅在95 nm～102．3 nm之间，每个频率下的基底膜的位移响应均有一个明显的峰值，如1 000 Hz频率激励下基底膜19 mm处出现最大峰值，这个峰值位置称为基底膜的最佳频率处，从而基底膜19 mm位置对应的最佳频率为1 000 Hz。为了表明基底膜的频率选择特性，图2．B将基底膜的位移幅值以卵圆窗的位移幅值为基准用dB坐标表示，从图中可以发现基底膜由底端到顶端的最佳频率是从10 kHz逐渐变化到100 Hz，基底膜底端对应高频，顶端对应低频。

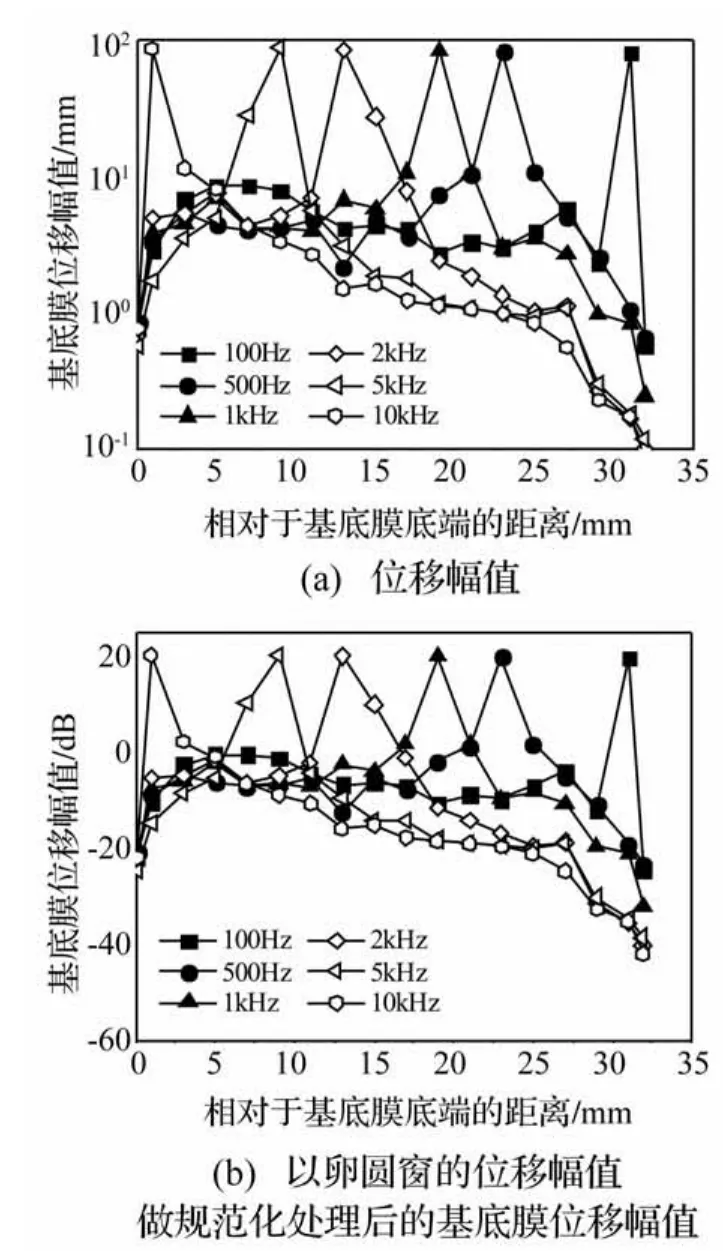
图2 不同频率下基底膜长度方向的位移Fig．2 Displacement of the BM from base to apex at frequencies of 100－10 kHz

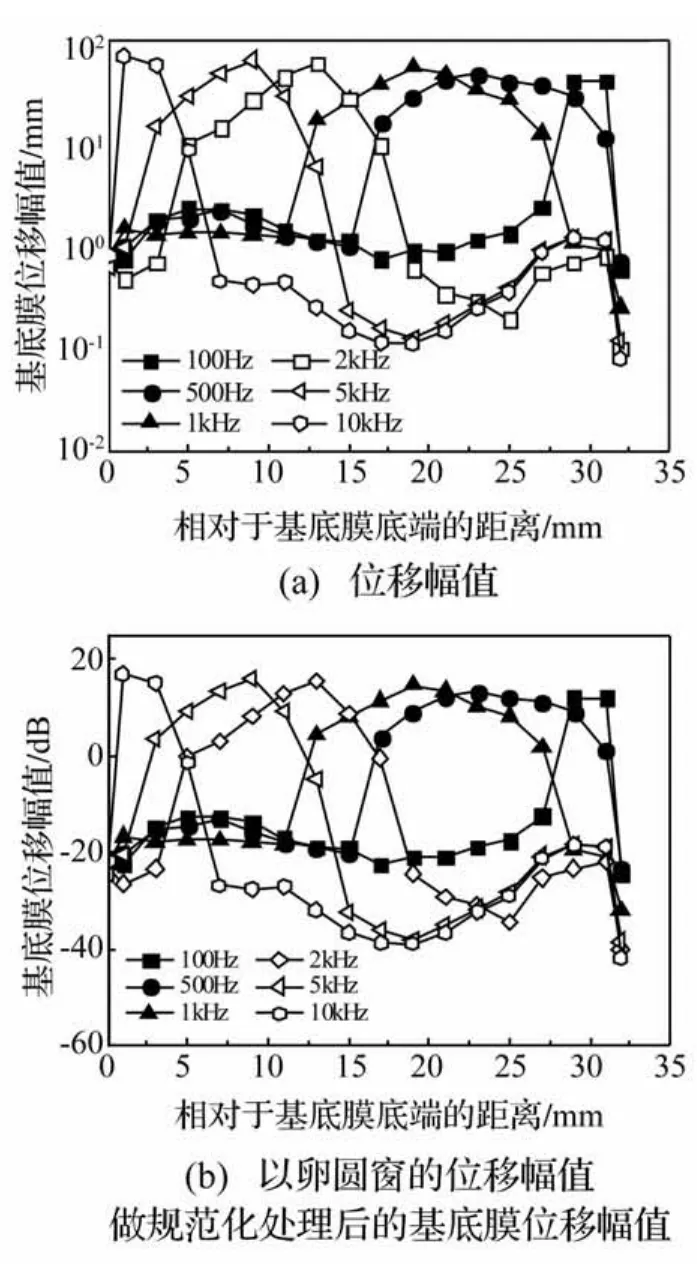
图3 0．5 mm模型不同频率下基底膜长度方向的位移Fig．3 Displacement of the BM from base to apex at frequencies of 100－10 kHz

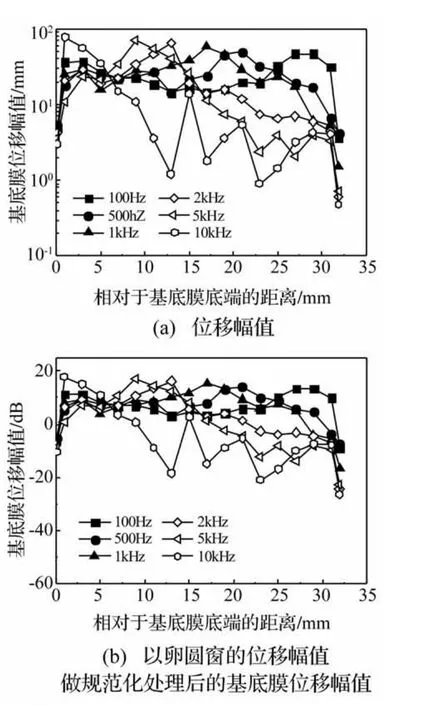
图4 0．01 mm模型不同频率下基底膜长度方向的位移Fig．4 Displacement of the BM from base to apex at frequencies of 100－10 kHz

2.2 其他蜗孔尺寸模型

蜗孔尺寸设置为0．5 mm时，由卵圆窗处10 nm幅值正弦激励下基底膜的位移响应见图3所示，图3包含了100～10 kHz范围内的6个不同激励频率下基底膜的位移响应，描述了基底膜的位移幅值沿着长度方向的分布情况。图3（a）用对数坐标形式表示基底膜的振动位移幅值，图3（b）是对卵圆窗位移做规范化处理后的基底膜位移（dB）。从图中可以看出，基底膜的最大振幅在39．7 nm～69．5 nm之间，同样每个频率下的基底膜的位移响应有一个明显的峰值。

当蜗孔尺寸设置为0．01 mm时，同样卵圆窗处10 nm幅值正弦激励下基底膜的振动响应见图4所示，图4（a）用对数坐标表示了基底膜的振动位移幅值，图4（b）将基底膜的振动幅值以卵圆窗输入的位移幅值为基底用dB表示。从图中可以看出与0．5 mm模型的响应类似，基底膜的响应相对比较平缓，幅值在46．65 nm ～77．4 nm之间。

2.3 不同蜗孔尺寸模型对比

图5是三种蜗孔尺寸的模型计算的基底膜不同位置上最佳频率对应的位移幅值，0．2 mm蜗孔尺寸模型计算的基底膜最佳频率处的位移幅值在100 nm左右，0．5 mm与0．01 mm蜗孔尺寸模型计算的基底膜最佳频率处的位移幅值在60 nm左右。0．2 mm模型计算的基底膜幅值在95 nm～102．3 nm之间，而0．5 mm模型计算的基底膜振幅在39．7～69．5 nm之间，0．01 mm模型计算的基底膜振幅在46．65～77．4 nm之间。从图中可以看出当蜗孔尺寸设置为0．2 mm时，基底膜的位移幅值比0．5 mm模型和0．01 mm模型的计算结果有了明显的提高。

图6表示了不同蜗孔尺寸模型计算的耳蜗频率－位置关系曲线，对比发现0．5 mm、0．2 mm和0．01 mm蜗孔模型的计算结果与Bekesy的实验数据［18］基本一致，在100 Hz、500 Hz和2 000 Hz时，三个模型的计算结果有些不同，但是在趋势上与实验数据符合较好，总的来说三个蜗孔尺寸的模型都可以反映基底膜的频率选择特性。

有限元模型计算的距圆窗12 mm处基底膜的位移响应见图7所示，其中基底膜的位移以卵圆窗的位移为基准用dB形式表示，并与Gudersen和Stenfelt的实验结果进行了对比［27－28］。实验数据测试的位置同是距卵圆窗12 mm处，实验曲线是基底膜的速度幅值，以卵圆窗的速度为基准用dB表示，所以其结果与位移曲线是一致的。从图中可以看出，实验数据的峰值在24 dB左右，而0．2 mm模型仿真结果的峰值为20．1 dB，0．5 mm模型和0．01 mm模型的峰值分别为15．6和16．4 dB，0．2 mm模型计算的结果与实验数据更接近。

图5 不同蜗孔尺寸时基底膜不同位置的最大振幅对比Fig．5 Comparison of basilar membrane longitudinal responses at different helicotrema dimensions

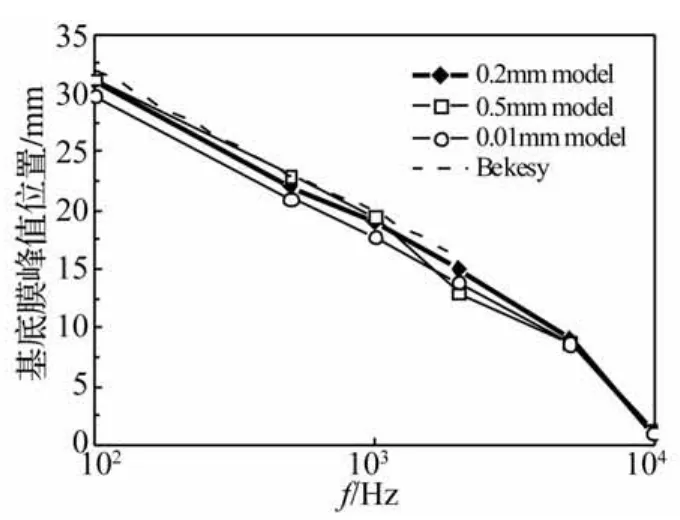
图6 不同蜗孔尺寸模型计算的耳蜗频率－位置关系图Fig．6 The place of maximum response on the BM vs．frequency at different helicotrema dimensions

图7 以卵圆窗位移为基准用dB形式表示的基底膜位移（基底膜距圆窗12 mm处）Fig．7 Response of the BM displacement normalized by OW displacement at x＝12 mm

3 讨 论

本研究建立的二维双向流固耦合耳蜗模型，首先希望本模型可以反映耳蜗中基底膜的振动响应机制。为了模拟镫骨底板的运动，在卵圆窗处施加正弦激励，从图2中可以看出，对于不同频率的激励，基底膜上均有一个不同位置的峰值与其对应，峰值位置随着频率的减小由耳蜗底端逐渐移动到顶端。这种变化与Bekesy［18］的实验数据是一致的，并且与其他的耳蜗模型计算结果［19－21］以及动物实验［22－26］相类似。本模型计算的基底膜响应与文献［6］中的耳蜗模型计算有所不同，文献［6］中的基底膜响应幅值在0．4 nm～130 nm之间，而本文三个有限元模型计算的基底膜振幅分别在95 nm～102．3 nm、39．7～69．5 nm和46．65～77．4 nm之间。这是因为文献［6］的模型是在外耳道处输入90 dB SPL的激励，卵圆窗处的振幅在100～10 kHz频率范围内不是相等的，而本模型采用了计算频段上相同的卵圆窗激励幅值，所以本模型在高频时的响应和低频时的响应相差不是很多。因此在用dB形式表示的基底膜位移图中，本文计算的结果与文献计算的结果比较接近。

通过图2、图3和图4的对比可以发现，0．2 mm模型计算的基底膜最佳频率处的响应更加尖锐，0．5 mm模型和0．01 mm模型基底膜最佳频率处的响应更加宽广，相比而言0．5 mm模型和0．01 mm模型计算的基底膜最佳频率处的响应幅值有了明显的降低。当以卵圆窗处激励幅值为基准，以dB形式表示基底膜振动幅值时，0．2 mm模型计算结果在19．55～20．19 dB之间，而0．5 mm模型的结果在12．04～16．83 dB之间，0．01 mm模型的结果在13．38～16．85 dB之间。通过图7中有限元模型计算的基底膜12 mm处的响应与实验数据的对比，发现0．2 mm模型的计算结果与实验报道的测试结果更接近，而0．5 mm模型与0．01 mm模型的计算结果与实验数据相差较大，所以当蜗孔尺寸设置为与真实尺寸一致时可以获得更好的结果。

图5是三种蜗孔尺寸模型计算的基底膜不同位置上最佳频率对应的位移幅值，0．2 mm蜗孔尺寸模型计算的基底膜最佳频率处的位移幅值在100 nm左右，0．5 mm与0．01 mm蜗孔尺寸模型计算的基底膜最佳频率处的位移幅值在60 nm左右。从图中可以看出，0．2 mm模型的基底膜振幅随着基底膜长度的增加，其最大振幅渐渐降低，降低的幅度不大。0．5 mm模型的最大振幅比0．2 mm模型相比较低，而且随着基底膜长度的增加而逐渐减小，在22．5 mm到32 mm之间趋于稳定。这可能是因为蜗孔尺寸从0．2 mm变为0．5 mm后，耳蜗中的流体流经耳孔更容易，故其流体的压力会有明显的降低，并且随着基底膜长度的增加，基底膜附近的流体压力逐渐减小，使得0．5 mm模型计算的基底膜最佳频率对应的振幅相比0．2 mm模型较小。当蜗孔尺寸设置为0．01 mm时，基底膜的最大振幅比0．2 mm模型的计算结果也有明显的降低，但是随着基底膜长度的增加，基底膜的最大振幅是逐渐增加的。这可能是因为蜗孔尺寸从0．2 mm变为0．01 mm后，蜗孔尺寸太小，从而导致耳蜗中的流体很难通过蜗孔流通到鼓阶中，所以耳蜗腔体中产生的流体压力较小。同时，当流体由大截面积的管道突然进入一个缩小的截面积时，流体的流速增加，流体压力会增加，所以耳蜗中流体压力沿着基底膜长度方向是逐渐增加的，使得基底膜的最大振幅随着基底膜长度的增加也是增大的。

图6中的耳蜗基底膜位置－频率关系图反映了基底膜的频率选择特性，对于不同频率的激励，在图中的曲线上可以找到对应的基底膜最大振幅位置。基底膜的刚度对基底膜位置－频率关系图影响较大，由于关于基底膜材料特性的报道的文献都是关于基底膜刚度的参数，这些参数不能直接用在模型中，在缺乏实验数据的情况下，只能通过与实验获得的基底膜位置－频率关系图对比，不断调整有限元模型中基底膜的当量弹性模量去调试基底膜的响应特性，最终获得近似的基底膜材料属性。通过图6的对比可以看出，三种蜗孔尺寸的有限元模型计算的耳蜗地图与Bekesy的实验数据趋势基本一致，这说明了本文中的有限元模型基底膜的频率选择特性与真实人耳耳蜗的特性接近，可以用来模拟内耳声音传递的特性。

4 结 论

本研究建立了二维双向流固耦合的耳蜗模型，将盘旋的耳蜗管道简化成拉直的规则形状，包含耳蜗中的流体和基底膜结构，通过耳蜗管道中的流固耦合模拟耳蜗的频率选择特性，模型计算结果与相关文献的实验数据相比具有较好的一致性。同时，本模型使用真实的蜗孔尺寸，并且建立了一个蜗孔尺寸偏大和一个蜗孔尺寸偏小的模型，对三个模型的计算结果进行对比分析，结果发现当设置真实的蜗孔尺寸时，基底膜的响应幅值与相关的实验以一致，所以耳蜗有限元模型中设置真实的蜗孔尺寸可以得到更准确的结果。

本研究建立的耳蜗模型是二维的流固耦合模型，相对来说三维的耳蜗双向流固耦合模型更接近真实的耳蜗结构，但三维模型中流体单元数量非常大，双向耦合计算时耗时比较长，对计算机的性能要求较高，所以这也需要一定的计算周期。本模型也没有考虑耳蜗管道中的盖膜、柯蒂氏器等微小器官，做为被动耳蜗模型忽略了微观结构的作用，三维的主动耳蜗流固耦合模型是下一步需要进行的工作。

［1］Allen J B．Two-dimensional cochlear fluid model New results ［J］．J Acoust Soc Am，1976，61（1）：110－119．

［2］Brass D．A macro-mechanical model of the guinea pig cochlea with realistic parameters［J］．J Acoust Soc Am，1999，104 （2）：894－907．

［3］Parthasarathi A A．Three-dimensional numerical modeling for global cochlear［J］．J Acoust Soc Am，1999，107（1）：474 －485．

［4］姚文娟，黄新生，李武，等．人工听骨不同接入方式对耳结构动力响应的影响［J］．医用生物力学，2010，25（3）：175 －181．

YAO Wen-juan，HUANG Xin-sheng，LI Wu，et al．Effect of different connecting methods for artificial ossicle on dynamic response of ear［J］．Journal of Medical Biomechanics，2010，25（3）：175－181．

［5］Böhnke F，Arnold W．3D Finite element modelof the human cochlea including fluid-structure couplings［J］．ORL，1999，61（5）：305－310．

［6］Gan R Z，Reeves B P，Wang X．Modeling of sound transmission from ear canal to cochlea［J］．Annals of Biomedical Engineering，2007，35（12）：2180－2195．

［7］Miller C．VLFEM analysis of a two-dimensional cochlear model［J］．Journal of Applied Mechanics，1985，52（4）：743 －751．

［8］王振龙，王学林，胡于进，等．基于中耳与耳蜗集成有限元模型的耳声传递模拟［J］．中国生物医学工程学报，2011，30（1）：60－66．

WANG Zhen-long，WANG Xue-lin，HU Yu-jin，et al．FEM simulation of sound transmission based on integrated model of niddle ear and cochlea［J］．Chinese Journal of Biomedical Engineering，2011，30（1）：60－66．

［9］刘迎曦，李生，孙秀珍．人耳传声数值模型［J］．力学学报，2008，40（1）：107－113．

LIU Ying-xi，LI Sheng，SUN Xiu-zhen．Numerical modeling of human ear for sound transmission［J］．Chinese Journal of Theoretical and Applied Mechanics，2008，40（1）：107 －113．

［10］Allen J B．Cochlear micromechanics：A physical model of transduction［J］．J Acoust Soc Am，1980，68（6），1660 －1670．

［11］Wittbrodt M J，Steele C R，Puria S．Developing a physical model of the human cochlea using microfabrication methods ［J］．Audiology and Neurotology，2006，11（2）：104－112．

［12］Chadwick R，Manoussaki D，Cai H．Effects of coiling on the micromechanics of the mammalian cochlea［J］．Journal of The Royal Society Interface，2005，2（4）：341－348．

［13］BöhnkeF，ArnoldW．Boneconductioninathree dimensional model of the cochlea［J］．ORL，2006，68（6）：393－396．［14］Hall J J W，Mueller H G．Audiologist's desk reference volumeⅡ：audiolologic management，rehabilitation and terminology［M］．Singular；1998．

［15］王学林，周健军，凌玲，等．含主动耳蜗的人耳传声有限元模拟［J］．振动与冲击，2012，31（21）：41－45．

WANG Xue-lin，ZHOU Jian-jun，LING Ling，et al．FE simulation of sound transmission in human ear with an active cochlea model［J］．Journal of Vibration and Shock，2012，31 （21）：41－45．

［16］Kim N，Homma K，Puria S．Inertial bone conduction：Symmetric and anti-symmetric components［J］．Jaro-Journal of the Association for Research in Otolaryngology，2011，12（3）：261－279．

［17］Ishii T，Takayama M，Takahashi Y．Mechanical properties of human round window，basilar and Reissner's membranes［J］．Acta Oto-Laryngologica，1995，115（S519）：78－82．

［18］Von Békésy G，Wever E G．Experiments in hearing［M］．McGraw-Hill New York；1960．

［19］Epp B，Verhey J L，Mauermann M．Modeling cochlear dynamics：interrelationbetweencochleamechanicsand psychoacoustics［J］．J Acoust Soc Am，2010，128（4）：1870 －1883．

［20］Yoon Y J，Puria S，Steele C R．Intracochlear pressure and derived quantities from a three-dimensional model［J］．The Journal of the Acoustical Society of America，2007，122（2）：952－966．

［21］Szalai R，Tsaneva-Atanasova K，Homer M E et al．Nonlinear models of development，amplification and compression in the mammalian cochlea［J］．Philos Transact A Math Phys Eng Sci，2011，369（1954）：4183－4204．

［22］Cooper N P．Basilar membrane mechanics in the hook region of cat and guinea-pig cochlea［J］．Hearing Research，1992，63（1992）：163－190．

［23］Khanna S，Leonard D．Measurement of basilar membrane vibrations and evaluation of the cochlear condition［J］．Hearing Research，1986，23（1）：37－53．

［24］Khanna S M，Leonard D G B．Basilar membrane tuning in the cat cochlea［J］．Science，1982，215：305－306．

［25］Nuttall A L．Laser doppler velocimetry of basilar membrane vibration［J］．Hearing Research，1990，51（1991）：203 －214．

［26］Rhrode W S．Observations of the vibration of the basilar membrane in squirrel monkeys using the mössbauer technique ［J］．J Acoust Soc Am，1971，49（4）：1218－1231．

［27］Stefan S，Puria S，Hato N et al．Basilar membrane and osseous spiral lamina motion in human cadavers with air and bone conduction stimuli［J］．Hearing Research，2003，181 （1）：131－143．

［28］Gundersen T，Sikkeland T．A study of the vibration of the basilar membrane in human temporal bone preparations by the use of the Mossbauer effect［J］．Acta Oto-Laryngologica，1978，86（1－6）：225－232．

Finite element model of human cochlea considering helicotrema size

XU Li-fu，TA Na，RAO Zhu-shi，TIAN Jia-bin
（State Key Laboratory of Mechanical System and Vibration，Institute of Vibration，Shock and Noise，Shanghai Jiaotong University，Shanghai 200240，China）

A 2-D finite element model of human cochlea was established here．This model included structures of oval window，round window and basilar membrane，the cochlea duct was filled with fluid．In order to study the effects of helicotrema on basilar membrane response，three different sizes of helicotrema were set up in the FE model．A two-way fluid-structure interaction numerical method was used to compute the response of the cochlea．The influence of the helicotrema was acquired and the frequency selectivity of the basilar membrane motion along the cochlear duct was predicted．These results agreed well with those of the reported experiments．The results indicated that the computed results closer to test data can be obtained with appropriate helicotrema size．

cochlea；helicotrema；basilar membrane；finite element model；fluid-structure interaction

TB 532；R318．01

A

10．13465／j．cnki．jvs．2014．23．011

国家自然科学基金资助项目考虑螺旋器的耳蜗非线性动力学模型研究（11072145）

2013－07－11 修改稿收到日期：2013－12－12

许立富男，硕士，1987年生

饶柱石男，博士，教授，博士生导师，1962年生