基于样本集的区间数灰靶分类决策模型及应用

梁燕华，郭 鹏，朱煜明

（1.杭州电子科技大学管理学院，浙江杭州 310018；2.西北工业大学管理学院，陕西西安 710072）

基于样本集的区间数灰靶分类决策模型及应用

梁燕华1，郭 鹏2，朱煜明2

（1.杭州电子科技大学管理学院，浙江杭州 310018；2.西北工业大学管理学院，陕西西安 710072）

基于灰靶思想的不确定背景分类决策问题分析，本文提出了区间数灰靶分类决策模型。该模型将灰靶决策拓展到决策信息为区间数的情况，提出了区间数的靶心距测度方法；根据靶心距提出了灰靶分类决策中的靶心分类临界值设置方法；以决策对象的靶心距与临界值之间的偏差总量最小为目标，建立了指标权重和分类临界值的确定模型；依据求解的权重与分类临界值对决策对象集进行分类评价。算例分析验证了该模型的有效性和可行性，可以很好地解决决策对象众多、分类数不确定等特性的多属性分类决策问题。

灰靶；区间数；分类；样本集；多属性决策

1 引言

多属性决策问题（MCDA）普遍存在于工程、社会和经济等系统之中，它是决策理论与方法研究的重要内容。多属性决策问题所面临的决策对象往往十分复杂，正确做出决策难度甚大，近几年来，国内外不少学者对多属性决策方法已进行了大量的研究，集中在多属性决策模型（如AHP、TOPSIS、ELECTRE、PROMETHEE和灰靶决策方法等）、不确定决策背景的方法（如区间数、模糊数、语言变量等）、实际问题的决策应用（如人力资源绩效评价、供应商选择评价）等方面［1-4］。灰靶决策通过基于标准模式（称为靶心）的距离大小来测度各决策对象的优劣，与经典的决策方法相比较，决策思想容易理解，得到了广泛应用，如解志坚［5］把灰靶理论应用于武器效能的评定；Feng Jianyou［6］将灰靶理论应用在对企业财务研究中，并对企业财务进行评定；刘思峰等［7］针对具有满意域的效益型、成本型和适中型等不同性质的决策目标，提出一种新的多目标加权灰靶决策模型，并应用于我国商用大型飞机项目的供应商选择上。在实际决策问题中，由于决策环境的复杂性、不确定性和模糊性，决策者往往无法给出效果测度的具体数值，指标值难以精确化，而只能以区间数的形式给出，很多文献涉及了区间数的理论方法研究［8］，如钟诗胜等［9］提出一种基于灰色系统理论的多指标区间数灰关联决策模型对大型水轮机的决策对象进行评价；王正新等［10］基于区间数距离和灰熵的决策分析，采用基于区间数的多目标灰色局势决策模型对企业的新产品决策进行分析。

在多属性决策过程中，许多分类问题需要同时考虑多种目标和因素，为取得更全面、准确的决策效果，一些学者提出了基于决策对象的多属性分类决策问题，实质是基于评价指标将决策对象按照某种特征进行类别划分，考虑到决策的工作量和问题复杂性，这种基于决策对象的分类决策过程具有广阔的应用前景［11-13］。已经有研究涉及了多属性分类决策模型［14-15］，但是缺乏不确定决策背景下的分类决策分析模型；现有基于决策对象集的分类决策方法，往往假设决策者的分类参考标准已知，实际上这种参考标准的确定相对复杂；另外，现有的方法根据参考标准分成了“优于”、“相当”和“劣于”等三类，现实情况的分类数往往需要根据实际情况来确定，因此，现有的方法应用存在局限性。在此基础上，本文基于灰靶思想的不确定决策背景下的决策模型分析，提出了基于样本集学习的一种新的多属性决策问题分类排序方法，由决策者先给出样本集并对它们进行分类，采用灰靶模型确定评价指标权重和分类临界值，由此对决策对象集进行分类评价排序。

2 问题描述

设A=｛A1，A2，…Ai，…，Am｝表示多属性决策问题的决策对象集，C=｛C1，C2，…，Cj，…Cn｝表示评价指标集，多属性决策问题就是要依据指标C对决策对象A按照一定的决策规则或者决策模型进行整合，获得对决策对象的评价、分类并助于决策的制定。本文提出多属性决策问题的分类评价模型，要求决策者基于自己的经验和偏好从决策对象集中选择一些决策对象并进行分类作为样本集T，即k个非空决策对象子集T1，…，Tk-1，Tk，其中：

构建指标权重和分类临界值求解模型对决策者给出的样本集k种分类进行研究，求出评价指标的权重和分类临界值。据此指标权重和分类临界值，按照样本的分类类型对决策对象集A或者新的决策对象集分类评价。由于问题的复杂性，决策者给出决策对象的属性值可能不是确定的数，分类数并不固定，分类参考点也不易确定，对此，本文依据灰靶决策思想，将正负理想点作为分类参考点，研究不确定决策背景下的分类决策模型，流程如图1所示。

图1 基于样本集的多属性灰靶分类决策流程图

3 基于区间数的灰靶分类决策模型

3.1 区间数标准化方法

（1）指标为效益型指标，指标值越大越好时

（2）指标为成本型指标，也就说指标值越小越好时，先用公式对指标

把成本型指标通过坐标平移处理数据使之转化为正向指标，最大程度上保留了原始数据的线性，并结合区间数的特殊性，指标区间数标准化上限值是原上限值除以该指标各决策对象的下限值之和；区间数标准化下限值是原下限值除以该指标各决策对象的上限值之和。该方法一定程度上放大了标准化后的指标取值区间，提高决策化矩阵的分辨度。

3.2 区间数的正负靶心选择及靶心距测度

对于指标Cj，决策对象样本集中第r个决策对象与指标正理想区间值的距离为），简记为，第r个决策对象与指标负理想区间值y-~j的距离为，简记为，公式如下［18］：

设指标权重向量W=（ω1，ω2，…，ωj，…，ωn），dr+表示第r个决策对象与正理想区间之间靶心距离，其数值越大，表示决策对象越差；数值越小则反之；dr-表示第r个决策对象与负理想区间之间靶心距离，数值越大，表示决策对象越好，数值越小则相反。dr+、dr-表达公式：

考虑定义基于正负靶心距的综合靶心值dr，dr越大，第r个决策对象越好，dr表达公示：

3.3 基于靶心距的分类规则及偏差分析

（1）靶心距分类

在基于样本集的多属性分类决策问题中，关键步骤就是根据决策者给出的样本集分类，反推出评价指标权重以及决策者把样本归类的分类临界值。针对决策者依据经验和数据给出的样本集及其分类，采用基于区间数的正负靶心距方法进行分析。假设Tk类优于Tk-1，hk-1和hk为判断第r个决策对象属于Tk类的临界值，根据综合靶心距的定义，决策对象越优，则综合靶心距越大，它们之间的关系描述如下：若第r个决策对象属于第Tk类，则有hk-1＜dr≤hk；若第r个决策对象属于第Tk-1类，则有hk-2＜dr≤hk-1；若第r个决策对象属于第T1类，则有0≤dr≤h1。

（2）决策对象与分类临界值之间偏差分析

在学习子集Tk中，共有mk个决策对象。若1≤r≤mk，第r个决策对象的靶心距dr小于或者等于临界值hk，定义偏差变量∈［0，1］，约束于条件hk-dr+≥0；第r个决策对象的靶心dr大于临界值hk-1，定义偏差变量∈［0，1］，约束于条件hk-1-dr+＜0，将样本子集Tk中每一个决策对象的dr都与临界值hk-1和hk进行比较，则Tk总偏差变量dk=

同理，得出样本子集Tk-1的总偏差变量dk-1，记为：

样本子集T1的总偏差变量d1，记为：

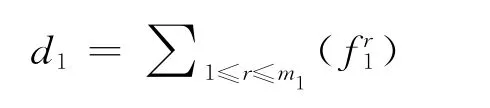
样本集T的k个子集的总偏差变量之和记为：

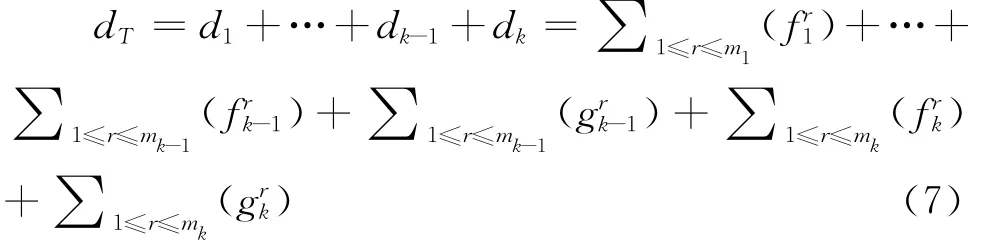
3.4 优化与求解权重模型

综合上面的分析，基于样本集建立最小偏差条件下的指标权重和分类临界值求解模型。

综上所述，可以得到基于样本集的区间数灰靶分类决策模型的步骤如下：

（1）决策者依据经验和对决策对象的偏好给出样本集并分类；

（2）对样本集进行靶心距测度和偏差分析，利用优化与求解模型，求出评价指标的权重向量W=（ω1，ω2，…，ωj，…，ωn）和分类临界值H=（h1，…，hk-1，hk）；

（3）利用已知的指标权重计算余下的决策对象综合靶心距，并根据分类临界值H=（h1，…，hk-1，hk）把A中余下的决策对象或者新的决策对象集分为k类：Ak，Ak-1，…，A1。

4 算例分析

4.1 背景描述

棕地指那些因存在一定程度污染已经废弃的或因污染而没有得到充分利用的土地及地上建筑物［19］。例如：废弃的工业厂房、加油站、干洗店等，多数位于城市的中心，优越的地理位置使得棕地再开发蕴涵着巨大的商机和经济利益［20］。许多学者对棕地再开发项目进行了研究，其中最著名的就是美国市长会议关于棕地再开发的报告，但是还没有研究为决策者提供不同棕地再开发项目成效分类的分析。本文选取某区域棕地再开发项目为应用对象，通过对再开发项目取得成效和影响进行系统地分析并分类，可以使政府充分认识到不同棕地再开发项目成效的差异化，以便制订针对性的政策和法规，来指导和促进不同区域的棕地再开发工作顺利开展和取得好的成效。

4.2 基础数据及计算分析

由于我国棕地再开发还处于起步阶段，缺乏已开发的棕地相关数据。因此，这部分应用研究采用美国部分区域的棕地再开发项目相关数据［21］，共4个评价指标，即每英亩修护成本C1（美元）、环境质量的改善C2（百分比）、每英亩带来永久的工作机会C3（人）、每英亩产生收益C4（美元）。在31个棕地再开发项目中，决策者选出8个项目作为样本集并分为三类，T3、T2、T1分别代表成效好、成效稍好和成效一般。如表1所示。

（1）样本靶心距计算

对样本集的数据运用公式（1）、（2）进行标准化处理，根据公式（3）计算指标在8个样本数据标准化后的正理想区间值：

根据公式（3）计算指标在8个样本数据标准化后的负理想区间值：

根据公式（4）计算第r项目关于四个指标的正负理想区间值的靶心距。四个指标权重为W=（ω1，ω2，ω3，ω4），则根据公式（5）计算第r项目离正理想区间值的靶心距dr+，第r项目离负理想区间值的靶心距dr-，并利用公式（6）计算含有未知权重变量的综合靶心距dr。

（2）权重与分类临界值计算

表1 样本集原始数据以及分类

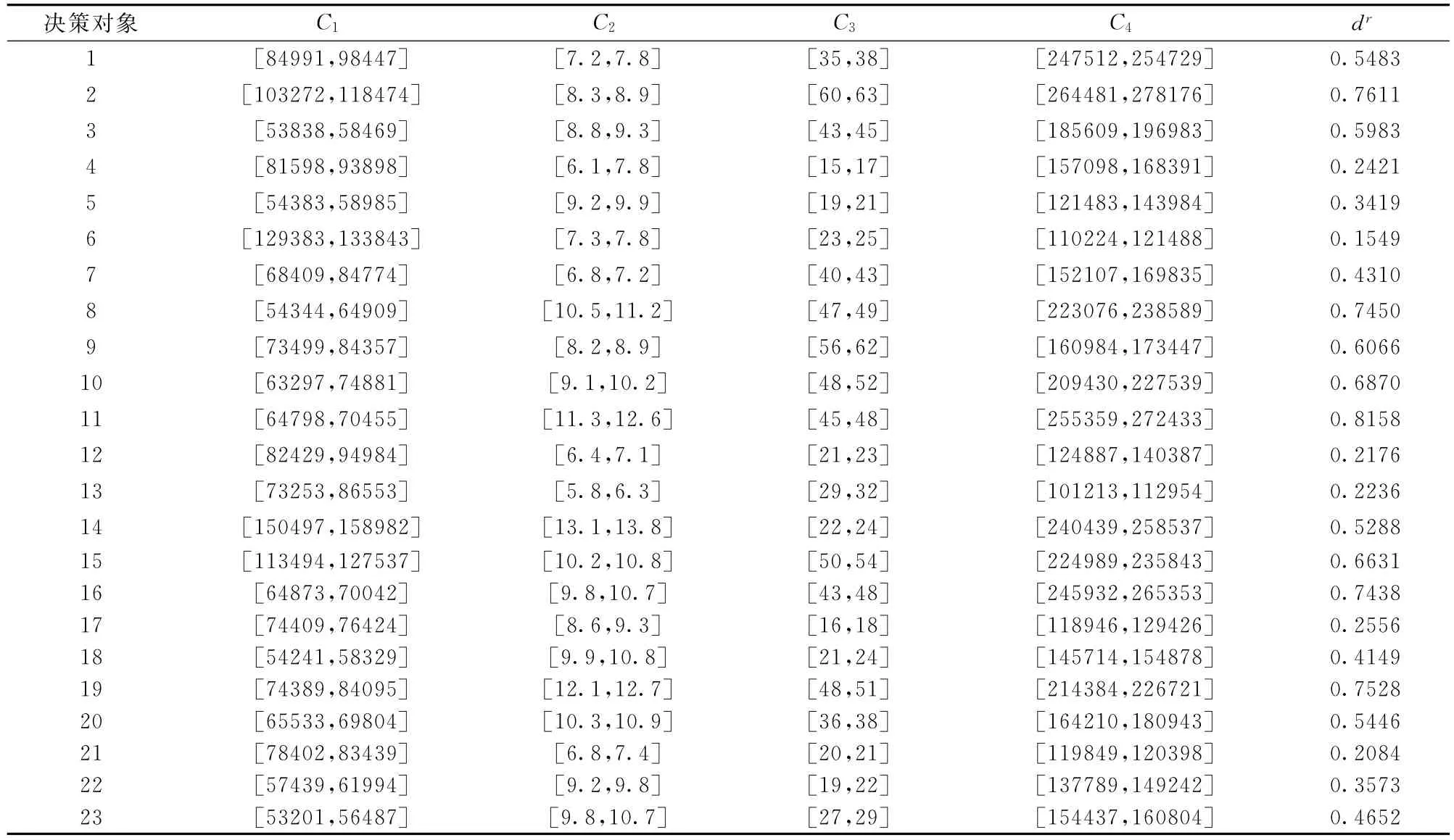
表2 决策对象集的原始数据及靶心距

把含有未知权重变量的靶心距与未知的分类临界值约束关系以及样本集偏差代入3.4建立的优化与求解权重模型，求得最小偏差下的指标权重和分类临界值：

ω1=0.1970，ω2=0.2622，ω3=0.2310，ω4= 0.3098 h1=0.9227，h2=0.6457，h3=0.2653。

4.3 对决策对象集的分类评价

决策对象集A其余项目数据如表2所示。

利用公式（1）和（2）对表2中的决策对象数据进行标准化处理，根据公式（3）和公式（4）计算决策对象的区间数正负靶心距，结合求解的指标权重计算决策对象的综合靶心距di，根据T3、T2、T1三类的分类临界值对决策对象集A（或者新的决策对象集）进行分类评价并排序：

（1）当0.6457＜di≤0.9227，第i项目归属于T3分类，共有7个，关系如下：

0.6457＜d15＜d10＜d16＜d8

＜d19＜d2＜d11＜0.9227

（2）当0.2653＜di≤0.6457，第i项目归属于T2分类，共有10个，关系如下：

0.2653＜d5＜d22＜d18＜d7＜d23

＜d14＜d20＜d1＜d3＜d19＜0.6457

（3）当0≤di≤0.2653，第i项目归属于T1分类，共有6个，关系如下：

0＜d6＜d21＜d12＜d13＜d4＜d17＜0.2653.

由算例知，决策者只需对8个棕地再开发项目的成效进行分类，根据区间数的灰靶决策模型，可以计算决策对象集A其余23个棕地再开发项目的综合靶心距并进行有效的分类，得到15、10、16、8、19、2、11项目再开发成效高的结论，有助于决策者进行项目间的对比研究，有效减少决策者的工作量并提高决策者的决策效率。

Chen Ye等［15］要求决策者为评价指标设定一个分类基准并将样本集分为三类，且决策信息为精确的数据，通过不断调整分类次序使总偏差变量达到可接受的水平，计算过程重复而复杂；本文提出的模型将分类种类由三类扩展成可以依据实际需要来定，决策者只需要对样本集进行分类而不需要为评价指标设定基准，依据样本集分类利用构建的模型直接求解指标权重和分类临界值，可以很好地应用在决策信息为区间数的不确定背景决策问题中，在解决类似的多属性分类决策问题上具有一定优势。

5 结语

本文针对多属性决策的决策对象众多以及复杂性问题，对灰靶决策模型深入分析，基于逆序的思想，提出了一种新的区间数灰靶分类决策模型，模型创新如下：（1）针对决策信息为区间数的多属性决策问题，提出了基于样本集的区间数多属性灰靶分类决策排序模型，将现有方法扩展到不确定决策环境之下；（2）采用灰靶决策思想进行了权重建模，简化了决策者选择设定基准参考的过程，根据靶心距离对分类偏差变量进行了设定；（3）为保持原始数据的线性，根据区间数的特性，提出新的适合区间数的数据标准化方法。应用该模型对区域棕地再开发项目成效进行分析，得出有效的排序和分类，便于政府了解不同棕地再开发项目的成效差异性，算例分析同时也验证了该方法的可行性和有效性。本模型主要适用于决策对象众多、决策信息是区间数、分类数不确定等条件下的多属性分类决策问题；未来的研究中，可以将决策信息扩展成语言变量和模糊数等不确定背景下的多属性分类决策问题中进行应用。

［1］匡奕军，范体军，李宏余.基于多属性决策的动态外包信息服务商选择［J］.系统工程理论与实践，2009，29（7）：77-85.

［2］Mundaca L，Neij L.A multi-criteria evaluation framework for tradable white certificate schemes.Energy Policy，2009，（37）：4557-4573.

［3］Willems P.A time series tool to support the multi-criteria performance evaluation of rainfall-runoff models.Environmental Modelling&Software［J］，2009，24（3）：311-321.

［4］El Hanandeh A，El-Zein A.The development and application of multi-criteria decision-making tool with consideration of uncertainty：The selection of a management strategy for the bio-degradable fraction in the municipal solid waste.Bioresource Technology［J］，2010，101（2）：555-561.

［5］解志坚，薄玉成.武器系统效能评定的灰靶理论应用［J］.兵工学报，2006，27（1）：162-165.

［6］Feng Jianyou，Zhang Hua.Grey target model appraising firm's financial status based on altman coefficients［J］. The Journal of Grey System，2006，53（7）：274-276.

［7］刘思峰，袁文峰，盛克勤.一种新型多目标智能加权灰靶决策模型［J］.控制与决策，2010，25（8）：1159-1163.

［8］王育红，党耀国.基于灰色关联系数和D-S证据理论的区间数投资决策方法.系统工程理论与实践，2009，29（11）：128-134.

［9］钟诗胜，王体春，丁刚.基于多指标灰区间数关联决策模型的产品案例设计［J］.控制与决策，2008，23（12）：1378 -1394.

［10］王正新，党耀国，宋传平.基于区间数的多目标灰色局势决策模型［J］.控制与决策，2009，24（3）：388-392.

［11］Doumpos M，Zopounidis C.Multicriteria decision aid classification methods［M］.Dordrecht，The Netherlands：Kluwer，2002.

［12］Chen Ye，Kilgour D M，Hipel K W.Multiple criteria classification with an application in water resources planning［J］.Computers Operations Research，2006，33（11）：3301-3323.

［13］Malakooti B，Yang Ziyong.Clustering and group selection of multiple criteria alternatives with application to space-based networks.IEEE Transaction on Systems，Man，and Cybern.B，Cybern.2004，34（1）：40-51.

［14］Zopounidis C，Doumpos M.Multicriteria classification and sorting methods：A literature review［J］.European Journal of Operational Research，2004，138（2）：229-246.

［15］Chen Ye，Marc K D，Hipel K W.Using a Benchmark in case-based multiple-criteria ranking［J］.IEEE transactions on systems，man，and cybernetics，2009，39（2）：358-368.

［16］李美娟，陈国宏，陈衍泰.综合评价中指标标准化方法研究［J］.中国管理科学，2004，12（10）：45-48.

［17］Wu Jun，Tian Xiaogang，Tang Ya，et al.Application of analytic hierarchy process-grey target theory systematic model in comprehensive evaluation of water environmental quality［J］.Water environment research，2010，82（7）：633-641.

［18］Luo Dang，Sun Li，Liu Sifeng，et al.Multi-objective grey target decision making methods under the information of three-parameter interval grey numbers［C］. Proceeding of Conference Proceedings-IEEE International Conference on Systems，Man and Cybernetics，Guangzhou，October 10-13，2010.

［19］朱建军，张丽丽，梁燕华，等.基于冲突主体不确定证据融合的灰靶决策方法［J］.控制与决策，2011，27（7）：1037-1041.

［20］Pagea G W.Characteristics and land use of contaminated brownfield properties in voluntary cleanup agreement programs［J］.Land Use Policy，2006，23（4）：551 -559.

［21］US Conference of Mayors（USM）.Recycling，Americas Land：A National Report on Brownfields Redevelopment［R］.Volume VI，2008.

A Sample-Set based Interval Gray Target Classification and Decision-Making Model and Its Applications

LIANG Yan-hua1，GUO Peng2，ZHU Yu-ming2
（1.Management School，Hangzhou Dianzi University，Hangzhou 310018，China；2.Management School，Northwestern Polytechnical University，Xi'an 710072，China）

Based on the analysis of gray target decision making under uncertainty，an interval gray target classification and decision-making model is put forward.In this model，the gray target decision-making is extended to uncertain circumstance in which the interval numbers serve as the decision-making information，and a method for measuring the target-center distances of the interval numbers is proposed.According to the target-center distance，a method for determining the critical values of target-center classification in the gray target classification and decision-making is presented.Besides，a determined model involving the target weights and the critical values of the classification is constructed，aiming at the minimum value of the accumulate deviation between the target-center distances in the case and the critical values.At last，classification and ranking of the new objects are conducted according to the calculated weights and the critical values of the classification.Case analysis shows the proposed model is effective and feasible.As a result，this model can be applied to multi-attribute classification decision-making problems with abundant objects and uncertain number of classification.

gray target；interval numbers；classification；sample-set；multi-attribute decision making

C943

：A

1003-207（2014）05-0098-06

2011-09-20；

2012-10-10

国家自然基金资助项目（71373964）；国家社会科学基金资助项目（10BJY024）；教育部人文社会基金资助项目（13YJC630177）；科研启动经费项目（KYS035613029）

梁燕华（1979-），女（汉族），河南南阳人，杭州电子科技大学管理学院，讲师，研究方向：多属性决策、项目评价.