欧债危机环境中资产组合ES模型比较研究

于文华，魏 宇，淳伟德

（1.成都理工大学商学院，四川成都 610059；2.西南交通大学经济管理学院，四川成都 610031）

欧债危机环境中资产组合ES模型比较研究

于文华1，2，魏 宇2，淳伟德1

（1.成都理工大学商学院，四川成都 610059；2.西南交通大学经济管理学院，四川成都 610031）

本文以中国上证综指、德国法兰克福DAX指数、美国S&P500指数为研究对象，分别运用DCC-GARCH及时变Copula-EVT模型建模，探讨了欧债危机爆发后股市间相依关系的变化状况。在此基础上，将三个股指收益两两组合，分别建立了各类模型假定下的资产组合预期损失ES模型，并通过后验分析方法，探讨了危机爆发后，各类ES风险模型测度精度的变化状况及对比结果。实证研究表明：欧债危机爆发后，时变Copula-EVT-ES的风险测度准确度明显高于DCC-GARCH-ES模型；边缘分布模型的选择对于时变Copula-EVT-ES模型的测度精度具有重要影响。综合对比分析发现，在金融市场极端波动的状况下，能够捕捉杠杆效应且善于刻画厚尾特征的时变t-Copula-AR（1）-GJR（1，1）-EVT-ES模型能够取得相对较好的风险测度效果。

欧债危机；DCC-GARCH；时变Copula；EVT；预期损失；后验分析

1 引言

资产组合风险评估一直是金融研究领域的核心内容，而资产间的相依关系测度则是组合风险计量的基础。随着经济全球化进程的加快，金融市场间的相互影响程度日益加深，在金融危机传染期间，金融市场或资产间的相依关系将剧烈波动而呈现出非线性、非对称的相依特征，因此以多元正态分布作为联合分布的假设在实证中得不到支持［1-2］。1999年，Embrechts等［2］将Copula理论引入金融领域，Copula函数善于捕获变量间非线性及非对称的相依关系，在金融市场研究中有着广阔的应用前景［3］。多数文献表明，基于Copula的风险评价方法优于使用多维正态分布或者多维t分布的传统方法，能够更加有效地测量风险［4-7］，尤其是结合EVT极值理论（Extreme Value Theory，EVT）的Copula-EVT模型，在尾部分析方面能够取得良好的风险测度效果［8-10］。风险评价模型的预测精度研究是资产组合风险管理的关键所在，已有学者在这方面进行了有益的探索：罗付岩等［11］将时变Copula的测度效果与常相关Copula函数进行对比，结果表明时变Copula-VaR模型更为准确。战雪丽、张世英［12］的研究发现，在刻画资产组合风险价值VaR方面，Copula-SV模型比Copula-GARCH具有优越性。苏静等［13］运用四类静态Copula函数对商业银行组合信用风险进行了度量。任仙玲等［14］构建了三类Copula-APD-GARCH模型，并进一步研究了均值-ES准则下的资产组合问题。

2009年底，欧债危机爆发，这是继次贷危机以来对全球金融市场影响深远的又一次危机传染，由此所引发的多米诺骨牌效应使得金融市场间的相关性愈加错综复杂。对于危机传染的研究相对较多，如Rodriguez［15］运用具有Markov转换参数的Copula模型研究了金融危机传染。龚朴等［16］运用时变t Copula模型分析了次贷危机对中国内地股市的影响。刘喜波等［17］运用Copula理论研究了次贷危机前后国际股票市场相关结构的变化。叶五一等［18］通过阿基米德Copula的变点检测方法分析了美国次级债金融危机对亚洲市场的传染效应。吴吉林等［19］运用机制转换动态Copula方法，研究了次贷危机中，中国沪市与美国股市、日本股市和香港股市间的相依性结构变化。王永巧等［20］基于时变Copula模型探讨了国际主要股市与中国股市间的风险传染问题。李堪［21］采用四类时变Copula函数，研究了2008年全球金融危机时期中国与美国、英国金融市场之间的金融危机传染效应的存在性问题。综上所述，从研究内容上看，当前文献主要侧重研究危机传染的机制及变点检测等，但却未能探及危机爆发后风险模型测度精度的比较问题；从研究方法上看，对于资产组合的风险评估，多数文献采用VaR风险价值模型进行测度，但VaR模型由于不满足“一致性风险测度（Coherent Risk Measurement）”而备受争议，在实际应用中有所限制，尽管已有文献结合Copula理论构建ES模型对组合风险进行计量［8-9、14］，但却尚未有文献基于欧债危机视角进行探讨。由此可见，无论是在研究视角、方法还是深度上，对于欧债危机环境中的资产组合风险测度都存在着值得进一步研究的方向。

鉴于以上分析，我们将以欧债危机为主线，着重探讨危机爆发后股市间尾部极值风险相依结构的变化，以及由此导致的资产组合风险模型测度精度的变化。本文的主要研究内容及特色在于：（1）在危机传染的环境中，比较和分析各类风险模型的测度精度，对于资产组合的优化及模型选择至关重要。由于组合资产风险评估过程中，不仅需要考虑单一资产的波动特征，更需要考察资产间的相依关系，因此我们将分别构建DCC-GARCH和时变Copula-EVT相依关系模型，一方面希望研究股市间风险相依强度在危机后的变化状况，另一方面也将在此基础上进一步对比研究相依关系模型对组合风险测度精度的影响作用。（2）预期损失ES（Expected Shortfall）模型对于“次可加性”的满足使其成为真正的“一致性风险测度”，特别是在描述金融资产极端损失方面，与VaR模型相比，ES模型更加符合金融实际操作的要求［22］，因此我们将构建各类模型假定下的资产组合ES模型，并通过严谨系统的后验分析方法（Backtesting Analysis），对各类ES风险模型的测度准确度进行比较研究。（3）在上述研究的基础上，重点探讨欧债危机爆发以后，市场极端波动的状况下资产组合ES风险测度模型的选择问题。

2 数据及计量模型描述

欧债危机是美国次贷危机的延续和深化，为考察继美国次贷危机之后，欧债危机对股市的影响，本文以2007年4月4日～2009年12月22日为欧债危机爆发前阶段，2009年12月23日～2012年6月15日为欧债危机爆发后阶段，进行比较研究。研究中所采用的股价指数均为每日收盘价，记为Pt，t= 1，2，3，…，N。文中定义各股指每日对数收益率rt如式（1）所示：

本文的数据采集于Yahoo财经网站，剔除掉交易时间不同的样本点，每种指数各有1116个样本点。计量分析所采用的软件主要为Rats 7.0和Matlab 7.0。在金融计量研究中，通常假定金融资产的日收益率rt满足：rt=μt+εt，为刻画股指收益序列的自相关性，运用AR（1）模型建模：

其中，ht是条件方差（Conditional Variance），zt为新生量（Innovation），令其服从学生t分布。关于波动率的模型构建，本文将分别采用GARCH（1，1）和GJR（1，1）两种形式，即：

其中：β0＞0，β1≥0，β2≥0。I（·）是指示函数（Indicator Function），即当（·）中的条件成立时，其取值为1，否则取值为0。模型中的参数c0，c1，β0，β1，β2，γ可通过极大似然估计方法（MLE）估计得到，结果如表1所示。

表1 AR（1）-GARCH（1，1）与AR（1）-GJR（1，1）模型的参数估计结果

表2 各股指收益标准残差序列的描述性统计量及诊断检验结果

由表1可见，股指收益模型中β1均大于0，β2均大于0.5，表明股指收益序列存在一定的持续性和波动聚集性的特点；β1+β2＜1，说明GARCH过程较平稳。除中国沪市外，德国与美国股市股指收益的GJR模型中，杠杆系数γ均不为0，说明存在杠杆效应，即波动的冲击具有非对称性。估计出模型参数之后，则可以根据式（5）过滤得到第i个股指收益最近n期的标准残差序列zi。对各标准残差序列zi进行检验，结果如表2所示。

由表2可见：LM检验结果显示标准残差序列不具有异方差性；Ljune-Box Q（20）统计值表明各标准残差序列均不拒绝无自相关性；而BDS检验结果显示，多数股指收益的标准残差序列不能拒绝满足独立同分布（Independent and Identically Distributed，i.i.d.）的原假设，少数未能通过严格BDS检验的标准残差序列也均通过了Ljune-Box Q检验，可认为其近似满足i.i.d.。

3 欧债危机后股市间风险相依关系的变化状况

金融资产间的相依关系计量是进行组合风险评估的关键环节，如果不能准确有效的描述资产间的相依关系，则将不可避免地影响到风险评估模型的测度准确性。为描述并对比考察金融资产间的动态相依关系，本文将分别采用DCC-GARCH及时变Copula-EVT模型进行刻画。

3.1 DCC-GARCH模型

Engle［23］提出的动态条件相关模型——DCCGARCH（Dynamic Conditional Correlation GARCH），能够对变量间的动态相依关系进行测定。为叙述方便，这里对资产组合中的两个资产分别使用下标1和2进行标注区分，DCC-GARCH模型主要包括以下方程：

为了便于和时变Copula-EVT模型所拟合的尾部极值动态相依系数进行对比说明，本文将DCCGARCH模型得到的动态相依系数ρt统一罗列在3.3节的表6当中。

3.2 时变Copula-EVT模型

Copula理论表明可以将一个联合分布分解为k个边缘分布和一个Copula函数，这个Copula函数描述了变量间的相关性，它也被称为连接函数［24］。由于EVT极值理论能够有效描述金融市场在极端波动情形下的风险状况，而这也正是金融风险管理的关注重点，因此本文将运用极值理论描述样本分布的非对称尾部特征，在此基础上构建时变Copula-EVT模型，从而刻画金融资产间的尾部极值动态相依关系。

3.2.1 结合EVT构建边缘分布模型

表3 两类边缘分布模型的K-S检验结果

构建时变Copula-EVT模型时，首先需要求得各股指收益的标准残差序列，并采用分段方法构造累积分布函数（Cumulative Distribution Function，CDF），即：对处于上下尾部阀值之间的标准残差采用高斯核密度估计（Gaussian Kernel Estimate）的方法来构造经验累积分布函数；而对于落入上下尾部的标准化残差，则运用提高门槛模型（Peaks-O-ver-Threshold，POT）建立累积分布函数。POT关注随机变量z超过某个阈值δ的条件极端损失分布函数Fδ。将z超过某个阈值δ但小于y的条件分布记为Fδ（y），随着门槛δ逐渐提高，极端损失分布Fδ（y）将收敛于广义帕累托分布（Generalized Pareto Distribution，GPD）Gξ，β［25-26］，即：

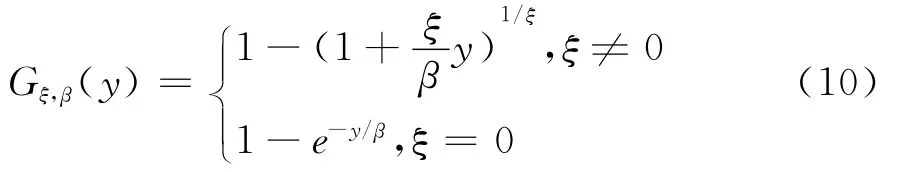
其中，ξ是尾部形状参数（tail parameter），β是标度参数（scale parameter）。β＞0，且当ξ≥0，z≥δ；当ξ＜0，δ≤z≤δ-β/ξ。表3中BDS的检验结果表明各标准残差序列满足或近似满足i.i.d.，符合EVT的适用前提，因此可以运用POT模型对各标准残差序列的尾部建模。本文参照Du Mouchel［27］选择10%的数据作为极值建模，并运用极大似然估计的方法估计得到GPD中的参数ξ、β。此外，构建Copula模型前，需要检验其边缘分布是否服从i.i.d.的（0，1）均匀分布，Kolmogorov Smirnov（KS）方法可用于这类检验。表3中K-S检验结果显示各边缘分布模型均通过了K-S检验，说明这里所构建的AR（1）-GARCH（1，1）-EVT、AR（1）-GJR（1，1）-EVT两类边缘分布模型都是合适的，可在此基础上进一步构建Copula模型。

3.2.2 时变Copula函数

除了与DCC-GARCH模型进行对比之外，我们还将考察不同的Copula函数对风险评估模型的影响，所以这里将分别采用两类时变Copula进行建模：t-Copula和Gaussian Copula。

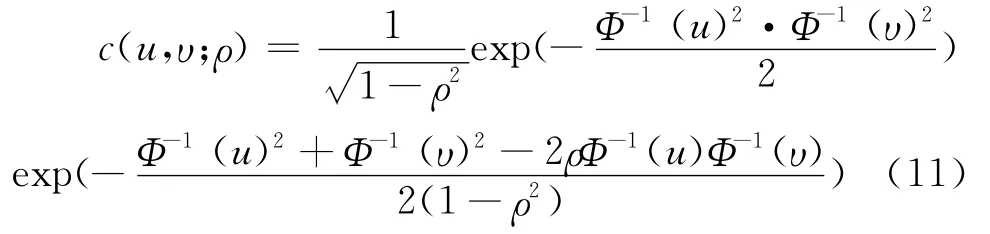
（1）二元Gaussian Copula函数的概率密度函数为［3］：

其中，Φ-1（·）是一元标准正态分布函数Φ（·）的逆函数，ρ∈（-1，1）为相关系数。

（2）二元t-Copula函数的条件概率密度函数为［］：

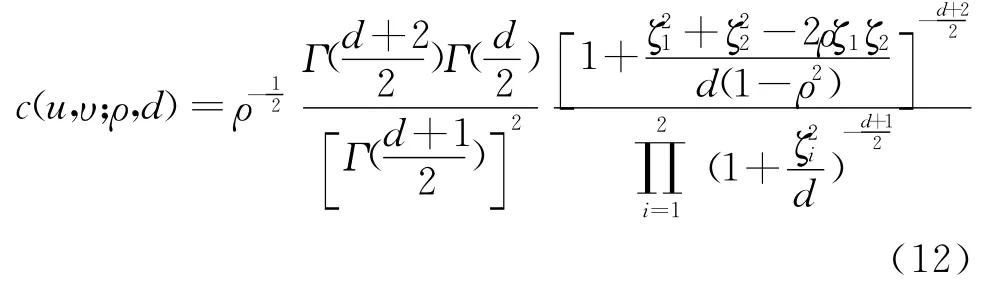
其中：ρ∈（-1，1）为相关系数，d是条件自由度，为简化模型，本文对于条件自由度d不考虑时变性。ζ1=Td-1（u），ζ2=Td-1（υ），Td-1（·）表示学生t分布函数Td（·）的逆函数。时变Gaussian Copula和时变t-Copula的动态相依系数ρt随时间的演化方程采用DCC方法［23］，即将相关系数矩阵ρt分解为：

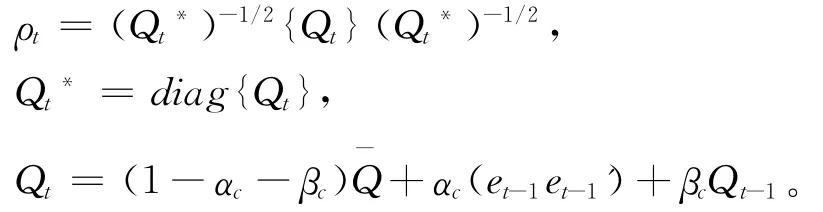
需要注意的是，这里的et为转化后的标准化残差序列（Transformed Standardized Residuals），它与所选用的Copula函数的类型有关：对于时变Gaussian Copula，et=（Φ-1（ut），Φ-1（υt））；而对于时变t Copula，et则定义为：et=（Td-1（ut），Td-1（υt））。Copula函数的参数估计方法使用IFM（inference for margins method），该方法是由Newey和McFadden［28］和White［29］提出的两步最大估计。IFM的基本思想是在估计得到边缘分布的参数之后，再估计得到Copula函数的相关参数，时变t Copula函数和时变Gaussian Copula函数的参数估计结果分别如表4和表5所示。

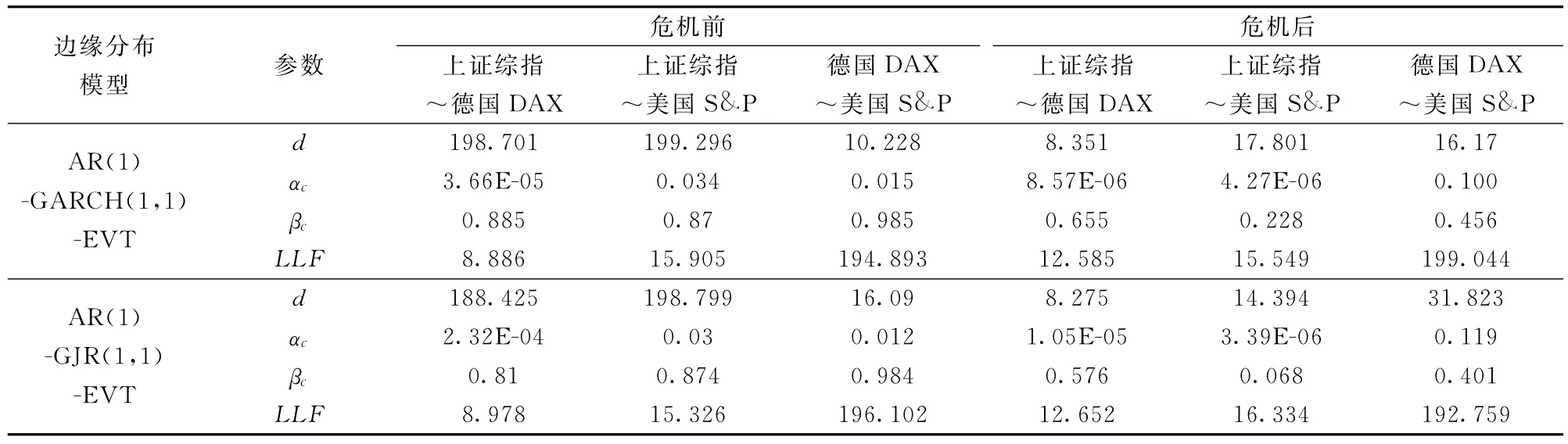
表4 时变t Copula函数的参数估计结果

表5 时变Gaussian Copula函数的参数估计结果

表6 危机前后股市间风险相依强度比较

3.3 欧债危机前后股市间风险相依强度比较

表6显示了危机前后股市间的相依强度及其变化趋势。总体上看，由DCC-GARCH模型的拟合结果表明，只有德国与美国股市间的整体风险相依关系在危机后有所增强；而由Copula-EVT模型所拟合的结果却显示，危机爆发后，各股市间的尾部极值相依关系均有不同程度的增强。

4 预期损失ES测度值的计算及后验分析

金融理论界和实务界所常用的VaR风险价值模型，其实质就是在一定的置信水平下，由于市场波动而导致金融资产在一段时期内可能出现的最大损失收益率。t时刻q分位数下的VaR估计表达式为：其中，zq为所考察的组合资产收益分布的q损失分位数，μt、σt分别为t时刻的资产组合的条件均值和条件波动率（本文将资产组合中各个资产设定为等权重）。通过式（13）可以分别计算得到各类模型假定下的VaR测度值。在VaR模型的基础上，Artzner等［30］提出了能够满足“一致性风险测度”的预期损失ES模型，并将其定义为：

ES测度值的估计过程为：将（0，q）区间做K等份，并由此得到K个VaR值，然后求取K个VaR均值以获得ES值。由此可见，ES预期损失模型充分考虑了超过VaR值的尾部极端分布状况，与现实金融风险的经济意义和测度意义更为贴合，其理论优势与实际应用价值也更为突出。为分析比较各类模型的ES测度效果，可采用自举法（Bootstrap）对ES风险模型进行后验分析，具体步骤可参阅文献Mc Neil和Frey［31］。在对不同模型假定下的ES估计精度进行分析时，采用后验分析的显著性p值作为评判标准，即p值越大则表示风险模型的预测准确度越高。表7罗列了在1%和0.1%两种分位数水平上的ES后验分析结果。

表7 不同ES风险计量模型的后验分析结果

由表7进行综合对比考察可见：

（1）欧债危机爆发后，ES风险模型测度精度的变化状况：在两种分位数水平上，本文所构建的ES风险模型大多通过了后验分析检验，但各类风险模型测度的准确度却有很大不同。危机爆发后，两类时变Copula-EVT-ES模型后验分析得到的p值均有不同程度的增大，这意味着在市场极端波动的情形下，这两类模型对于资产组合的风险测度更加准确。

（2）边缘分布模型的选择，对于时变Copula-EVT-ES模型的影响：在构建时变Copula模型的过程中，本文分别运用了AR-GJR-EVT和ARGARCH-EVT两类边缘分布模型，而通过比较可以发现，边缘分布的选择确实对时变Copula-ES模型的测度准确度具有重要影响。具体来讲，对于各个资产组合，在危机爆发前，由两类边缘分布模型构造的Copula-ES模型的测度精度并无显著差异，但危机爆发后，在AR-GJR-EVT基础上计算的时变Copula-ES模型的测度准确度却相对较高。尤其是对于“上证综指～美国S&P”这一资产组合，在0.1%的分位数水平上，无论危机前后，DCCGARCH的测度精度均高于以AR-GARCH-EVT作为边缘分布的Copula-ES模型；而当改变边缘分布模型，即通过AR-GJR-EVT构造边缘分布时，其对应的Copula-ES模型的预测精度显著提高。事实上，由于在构建Copula模型时，可以灵活地选择边缘分布，这就为提高基于Copula的风险模型的测度精度提供了广阔的应用空间，因此Copula模型在刻画相依关系及资产组合风险测度等方面具有非常明显的优势。

（3）杠杆效应项的纳入，对于时变Copula-EVTES风险模型的影响：欧债危机爆发以后，在时变Copula-ES模型中纳入杠杆效应项，有助于提高其风险测度的准确性。由表2观察对比杠杆系数γ在危机后的变化状况将有助于理解这一现象：GJR模型中的参数γ为杠杆系数，用以衡量资产收益对市场波动冲击的反应。危机发生以后，德国DAX与美国S&P500指数收益率对应的杠杆系数γ均有不同程度的增大，杠杆效应较危机前更为显著，因而对于这一资产组合，时变Copula-AR-GJR-EVT-ES模型的测度准确度明显高于其他模型。而对于其他两项资产组合，危机爆发后，在剧烈波动的金融环境中，时变Copula-AR-GJR-EVT-ES模型依然取得了较高的风险测度准确度。

（4）不同风险模型对于预期损失ES测度精度的影响：总体而言，风险测度效果最好的模型为时变t-Copula-EVT-ES模型，时变Gaussian Copula-EVT-ES模型次之，但其测度准确度依然高于DCCGARCH-ES模型，特别是在危机爆发以后，三类模型预测精度的差异更为明显。这一实证结果具有两个方面的意义：第一，欧债危机爆发以后，与DCCGARCH-ES模型相比，结合EVT极值理论的时变Copula-ES模型对资产组合尾部极值风险的测度更为准确。第二，在市场极端波动状况下，善于刻画厚尾分布特征的时变t-Copula-EVT-ES模型表现出良好的风险测度效果。

5 结语

本文分别构建了DCC-GARCH和时变Copula-EVT模型，深入研究了欧债危机后股市间尾部极值动态风险相依强度的变化状况；在此基础上构建了预期损失ES风险测度模型，并对各类模型的测度精度进行了对比研究。本文所取得的主要实证研究结论包括：

（1）与DCC-GARCH-ES模型相比，时变Copula-EVT-ES模型在危机后能够取得相对较高的风险测度效果。由于时变Copula-EVT模型能够较好的刻画尾部极值相依关系，因此在金融市场剧烈动荡的环境中，特别是危机传染期间，这类风险模型值得特别关注。

（2）边缘分布的选择对于时变Copula-EVT-ES模型的测度精度具有重要影响。面对金融市场系统性风险的冲击，将杠杆效应纳入Copula-EVT-ES模型计量中，有助于提高其风险测度的准确性。正因如此，欧债危机爆发后，能够捕捉杠杆效应且善于刻画厚尾特征的时变t-Copula-AR（1）-GJR（1，1）-EVT-ES模型取得了很好的风险测度效果。

（3）欧债危机爆发以后，金融资产收益的分布状况及资产间的相依结构发生改变，各类风险评价模型的预测效果具有明显差异，投资机构应根据国际金融大环境、各国金融市场的具体特点及资产组合的实际分布状况，对各类风险模型的测度精度进行对比分析，选择合适的模型进行风险评估及预测。由于预期损失ES模型能够着重考察资产组合分布超过VaR测度值的尾部部分，因此在刻画金融资产极端损失方面具有独到的优势和重要的现实意义。而在金融实践中，由于各类模型的风险测度效果存在明显差异，因此投资者不仅应特别重视ES模型与VaR模型的有机结合，更需要对比研究各类风险评价模型的测度效果，择优选用。

此外，本文在实证研究中，只比较了AR-GJREVT和AR-GARCH-EVT这两类边缘分布对于Copula-ES模型测度精度的影响。而Copula函数所具备的优良数学特性之一就是可以有选择地构造边缘分布，且边缘分布的选择确实对Copula-ES模型的风险测度效果具有重要影响，因此我们将考虑把其他类型的边缘分布纳入到Copula-ES风险模型中并作对比研究。最后，关于如何对资产组合中的各类资产分配权重从而达到组合风险最小的问题，也值得我们作更进一步的深入研究和探讨。

［1］Patton A J.On the out-of-sample importance of skewness and asymmetric dependence for asset allocation［J］. Journal of Financial Econometrics，2004，2（1）：130-168.

［2］Embrechts P，Mc Neil A J，Straumann D.Correlation：Pitfalls and alternatives［J］.Risk，1999，（12）：69-71.

［3］韦艳华，张世英.Copula理论及其在金融分析上的应用［M］.北京：清华大学出版社，2008.

［4］王久胜，包卫军，胡杰.基于多维Gumbel Copula函数的投资组合VaR分析［J］.数理统计与管理，2010，（1）：137-143.

［5］柏满迎，孙禄杰.三种Copula-VaR计算方法与传统VaR方法的比较［J］.数量经济技术经济研究，2007，（2）：154-160.

［6］杨湘豫，夏宇.基于Copula方法的开放式基金投资组合的VaR研究［J］.系统工程，2008，26（12）：40-44.

［7］周孝华，张保帅，董耀武.基于Copula-SV-GPD模型的投资组合风险度量［J］.管理科学学报，2012，15（12）：70 -78.

［8］应益荣，詹炜.资产组合ES风险测度的Copula-EVT算法［J］.系统管理学报，2007，16（6）：602-606.

［9］刘晓星，邱桂华.基于Copula-EVT模型的我国股票市场流动性调整的VaR和ES研究［J］.数理统计与管理，2010（1）：150-161.

［10］江红莉，何建敏，庄亚明，等.投资组合风险测度——基于FIGARCH-EVT-Copula方法［J］.北京理工大学学报（社会科学版），2012（1）：44-49.

［11］罗付岩，邓光明.基于时变Copula的VaR估计［J］.系统工程，2007，（8）：28-33.

［12］战雪丽，张世英.基于Copula-SV模型的金融投资组合风险分析［J］.系统管理学报，2007，16（3）：302-306.

［13］苏静，杜子平.Copula在商业银行组合信用风险度量中的应用［J］.金融理论与实践，2008，（5）：6-8.

［14］任仙玲，叶明确，张世英.基于Copula-APD-GARCH模型的投资组合有效前沿分析［J］.管理学报，2009，6（11）：1528-1535.

［15］Rodriguez J C.Measuring financial contagion：A copula approach［J］.Journal of Empirical Finance，2007，14（3）：401-423.

［16］龚朴，黄荣兵.次贷危机对中国股市影响的实证分析——基于中美股市的联动性分析［J］.管理评论，2009，（2）：21-32.

［17］刘喜波，林泽波.次贷危机后国际股票市场相关性变动的Copula分析［J］.数学的实践与认识，2009，39（24）：31-35.

［18］叶五一，缪柏其.基于Copula变点检测的美国次级债金融危机传染分析［J］.中国管理科学，2009，17（3）：1 -7.

［19］吴吉林，张二华.基于机制转换混合Copula模型的我国股市间极值相依性［J］.系统工程理论与实践，2012，32（8）：1662-1672.

［20］王永巧.基于时变Copula的金融开放与风险传染［J］.系统工程理论与实践.2011，31（4）：778-784.

［21］李堪.基于时变Copula理论的金融危机传染效应存在性研究——以2008年全球金融危机为例［J］.世界经济与政治论坛，2012（2）：41-54.

［22］王鹏.基于时变高阶矩波动模型的VaR与ES度量［J］.管理科学学报，2013，16（2）：33-45.

［23］Engle R.Dynamic conditional correlation：A simple class of multivariate GARCH models［J］.Journal of Business and Economics Statistics，forthcoming，2002，20（3）：339-350.

［24］张尧庭.连接函数（copula）技术与金融风险分析［J］.统计研究，2002，4：48-51.

［25］Pickands J.Statistical inference using extreme order statistics［J］.The Annals of Statistics，1975，41（3）：1119-1131.

［26］Balkema A A，de Haan L.Residual life time at great age［J］.Annals of Probability，1974，14（2）：792-804.

［27］Du Mouchel W M.Estimating the stable index 2 in order to measure tail thickness：A Critique［J］.Annals of Statistics，1983，（11）：1019-1031.

［28］Newey W K，McFadden D.Large sample estimation and hypothesis testing［J］.Handbook of Econometrics，1994，4：2111-2245.

［29］White H.Estimation，inference and specification analysis［M］.New York：Cambridge University Press，1994.

［30］Artzner P，Delbaen F，Eber J M，et al.Coherent measures of risk［J］.Mathematical Finance，1999，9（3）：203 -228.

［31］Mc Neil A，Frey R.Estimation of tail-related risk measures for heteroscedastic financial time series：An extreme value approach［J］.Journal of Empirical Finance，2000，7（3）：271-300.

Comparatively Study on Portfolio ES Models under European Debt Crisis

YU Wen-hua1，2，WEI Yu2，CHUN Wei-de1
（1.Commercial College，Chengdu University of Technology，Chengdu 610059，China；2.School of Economics and Management，Southwest Jiaotong University，Chengdu 610031，China）

DCC-GARCH and time-varying Copula-EVT models are constructed respectively to discuss the changes of dependencies between stock markets after the outbreak of European Debt Crisis.2-2 combinations of the stock index returns are made，the portfolio ES models are established under various models assumed，and the measurement accuracy of all ES models are compared and discussed after the crisis through backtesting analysis.China Shanghai Composite Index，the Frankfurt DAX index of Germany and S&P500 Index of the United States are used to make empirical experiment.Empirical studies show that after the crisis，the risk measure accuracy of time-varying Copula-EVT-ES models are significantly higher than DCC-GARCH-ES.Further，it is important to select marginal distribution for time-varying Copula-EVT-ES models.Finally，under extremely volatile financial market conditions，the time-varying t-Copula-AR（1）-GJR（1，1）-EVT-ES model，which is good at capturing the leverage effect and characterizing fat tails，achieves relatively better risk measure results.

European debt crisis；DCC-GARCH；time-varying copula；EVT；ES；backtesting analysis

F830.9；F222.3

：A

1003-207（2014）05-0008-08

2012-07-16；

2013-11-02

国家自然科学基金资助项目（71071131，71090402，71371157）；高等学校博士学科点专项科研基金资助课题（20120184110020）；中央高校基本科研业务费专项资金资助项目（SWJTU11ZT30，SWJTU11CX137，SWJTU12CX120）；国家社会科学基金（12BGL024）；成都理工大学金融与投资科研创新团队（KYTD201303）；四川省软科学研究计划项目（2013ZR0068）；成都理工大学中青年骨干教师培养计划项目（JXGG201420）；四川省教育厅人文社科重点项目（14SA0039）

于文华（1976-），女（汉族），辽宁大连人，成都理工大学商学院，副教授，研究方向：金融市场与风险管理.