MT信号处理中小波分析与Hilbert-Huang变换的比较

蔡剑华,胡惟文, 覃业贵, 陈卿冶



MT信号处理中小波分析与Hilbert-Huang变换的比较

蔡剑华*1,胡惟文1, 覃业贵2, 陈卿冶1

(1. 湖南文理学院 物理与电子科学学院,湖南 常德, 415000; 2. 解放军93062部队, 吉林 吉林, 132102)

以实测大地电磁信号为分析对象, 对比研究了小波分析和Hilbert-Huang变换在大地电磁(magneto- telluric, MT)信号分解和时频分析上面的特点. 给出了小波分析和Hilbert-Huang变换的数学原理, 分析了2种方法在MT信号分解中的分解方法及其物理意义, 讨论了2种方法在MT信号时频谱表征能力上的异同, 为大地电磁信号分析方法的选择提供用了有价值的参考.

大地电磁信号; Hilbert-Huang变换; 小波分析; 分解; 时频分析

非线性信号处理方法是分析、处理非平稳大地电磁信号的有力工具[1], 其中小波分析和Hilbert- Huang变换在地球物理领域应用的较为广泛, 他们都能将信号进行自适应的分解, 并得到时频谱图, 揭示信号的时变特征, 尤其在希望获得频率成分随时间变化规律的地震信号处理和大地电磁法中应用较多[2—4]. 本文以实测大地电磁信号为分析对象, 对比研究小波分析和Hilbert-Huang变换在大地电磁信号分解和时频分析上面的优缺点, 试图为大地电磁信号分析方法的选择提供用有价值的参考.

1 小波变换

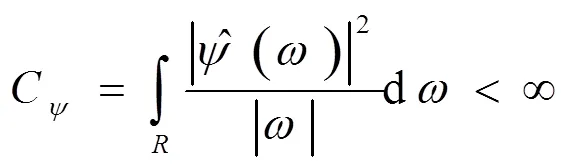
则()被称为一个基本小波函数, 将小波函数()进行伸缩和平移变换就可以得到一组小波[5].

在连续情况下, 小波为:

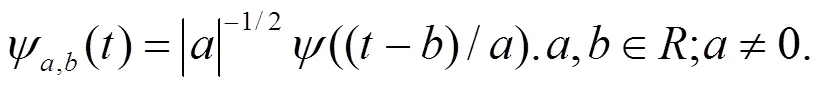
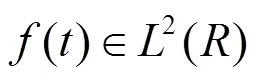
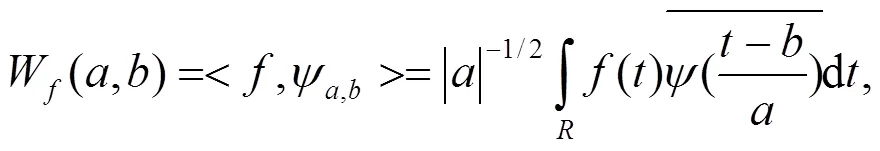
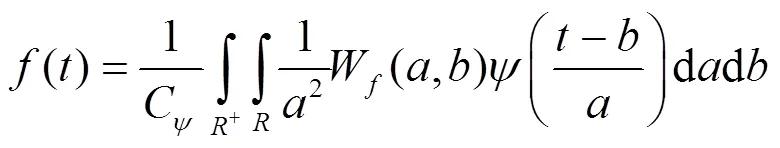
通过适当地选择尺度因子和平移因子, 可得到一个伸缩窗[6].

在离散情况下, 小波为:

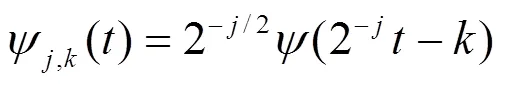
与函数()相应的离散小波变换系数及其重构公式为:

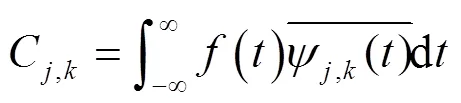
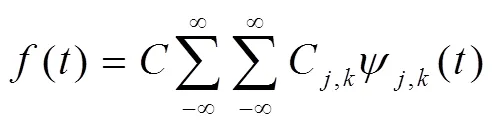
式(7)中是一个与信号无关的常数.

2 Hilbert-Huang变换

2.1 经验模态分解

经验模态分解(empirical mode decomposition, EMD)是依据信号本身的时间尺度特征, 将信号分解为一组模态函数(intrinsic mode function, IMF)[11], IMF满足以下2个定义条件[7]: ①对于一列数据极值点和过零点数目必须相等或至多相差一点; ②在任意点, 由局部极大点和极小点构成的两条包络线的平均值为0. EMD分解方法如下[7]: ①找出信号()的所有极大点和极小点, 将其用三次样条函数分别拟合为原数据序列的上、下包络线, 上、下包络线的均值为平均包络线1, 将原数据序列减去1可得到一个去掉低频的新数据序列1. 一般1不是一个平稳数据序列, 为此重复以上过程次, 使所得到的平均包络线趋于0, 此时的1n就是第1个IMF(1), 它表示信号数据中的最高频成分; ②用()减去1得到一个去掉高频成分的新数据序列, 重复步骤(1), 得到一系列c和最后一个序列r,r代表()的均值或趋势项. 那么原序列()可表示为IMF分量和一个残余项的和:

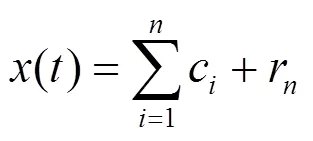
2.2 Hilbert变换与时频谱

获得IMF分量后, 就可以对每阶IMF(设为())作Hilbert变换, 得到:

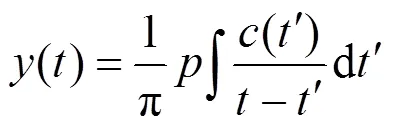
为柯西主值.()和()共同组合为一解析信号(), 采用极坐标形式表示:

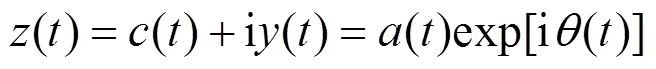
其中:

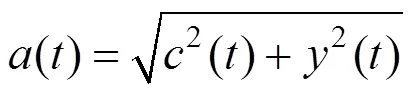
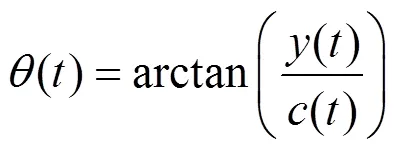
根据瞬时频率的定义:

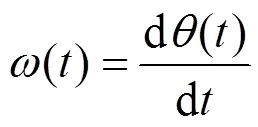
对每一阶IMF作Hilbert变换, 并求出相应解析函数的幅值谱和瞬时频率, 从而原始信号可以表示为[8]:

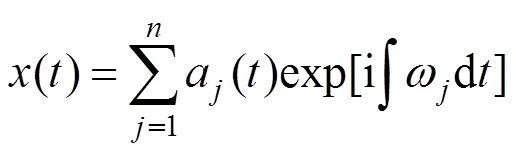
可见, 信号的幅值能表示为时间、瞬时频率的函数(,), 从而获得信号幅值的时间和频率分布即Hilbert谱.

3 MT信号的小波分解与时频谱

图1中EH-4仪器采用低频工作模式, 采样率为12 kHz. 由于数据量庞大, 此处仅取E分量的4 096个点进行分析. 小波变换在不同尺度下分解信号是多分辨率的, 小波变换的尺度因子使得小波变换具有“变焦距特性”, 被誉为数学上的显微镜, 小波变换中可改变尺度因子得到一个伸缩窗. 图2(a)所示为利用sym5小波基对实测数据进行分解的小波分解图. 图中, a6及d1—d6是小波分解后得到的小波分量, 其中a6为第6层分解的近似系数、d1—d6为前6层分解的高频系数, 各层系数对应于从高频到低频的滤波过程.

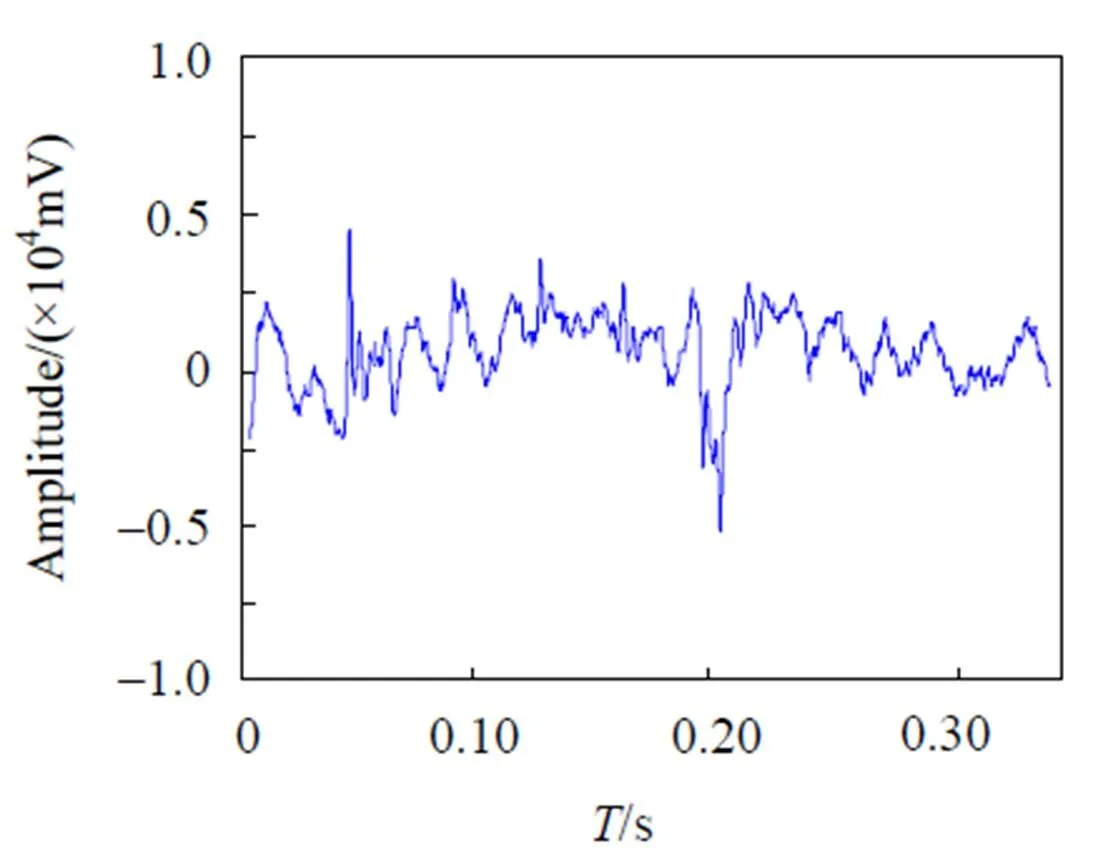
图1 原始的大地电磁信号

小波分解中小波基函数的选择不是任意的, 也不是唯一的. 因此, 小波基的选择是小波分析在实际应用中的一个重要问题. 如图2(b)所示为相同的图1所示信号采用db5小波基分解后的分解图. 可见, 其分解系数与图2(a)所示是不尽相同的, 尤其是高频部分的信息. 同一个问题小波基不同, 其结果也不同, 甚至相差很大.

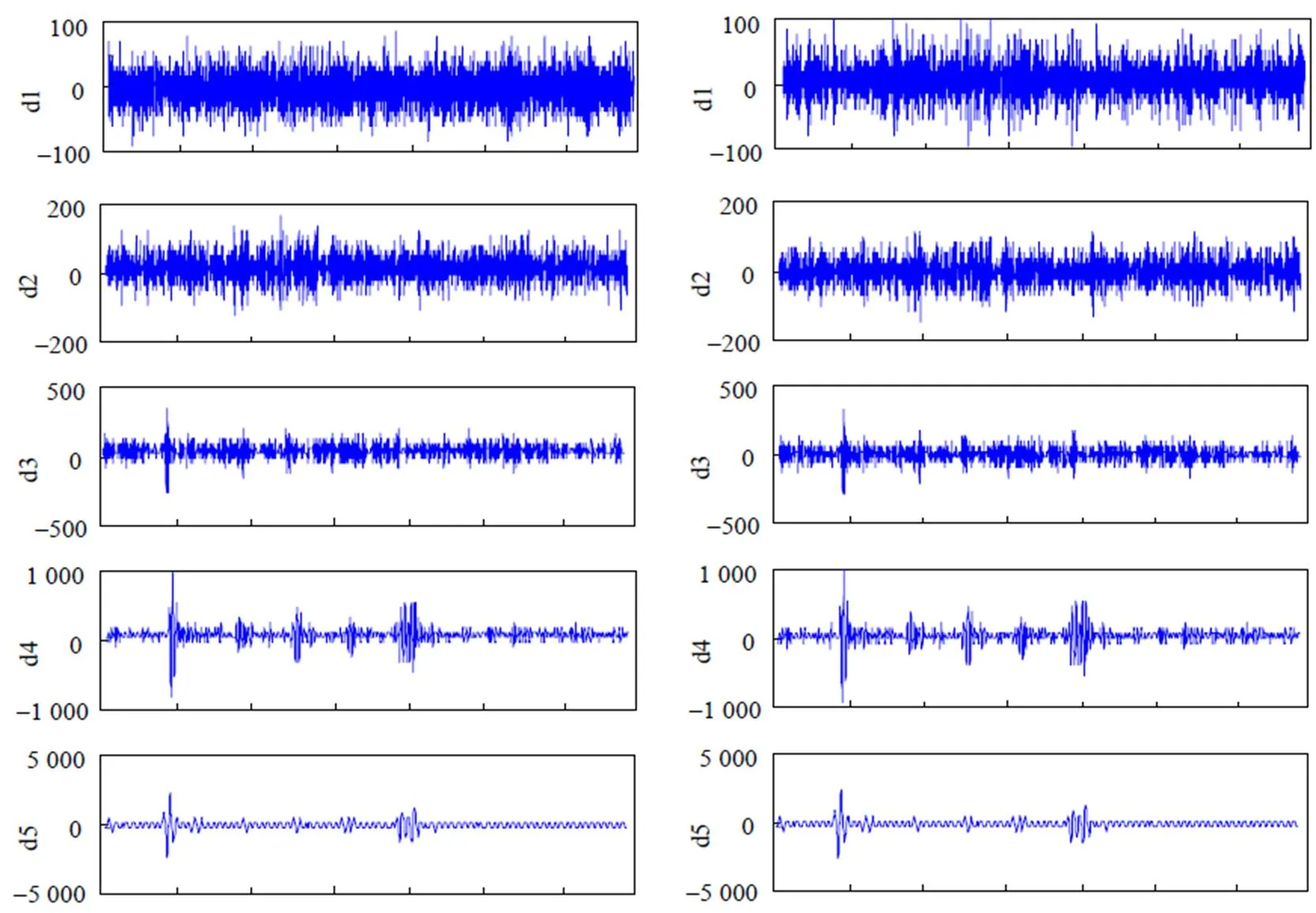
图3所示为利用sym5小波基分析得到的大地电磁信号时频谱图. 从图3中可清楚地看出大地电磁信号能量随时频的分布情况, 谱图表现出良好的局部化特征, 较精确地描述了大地电磁信号的时频分布. 但也可以清楚地看到在大地电磁信号小波谱中, 能量呈分散特征, 分别率也不高, 存在混叠的现象, 且除主成分外还存在的谐波成分, 其对应的频率范围也被展宽.

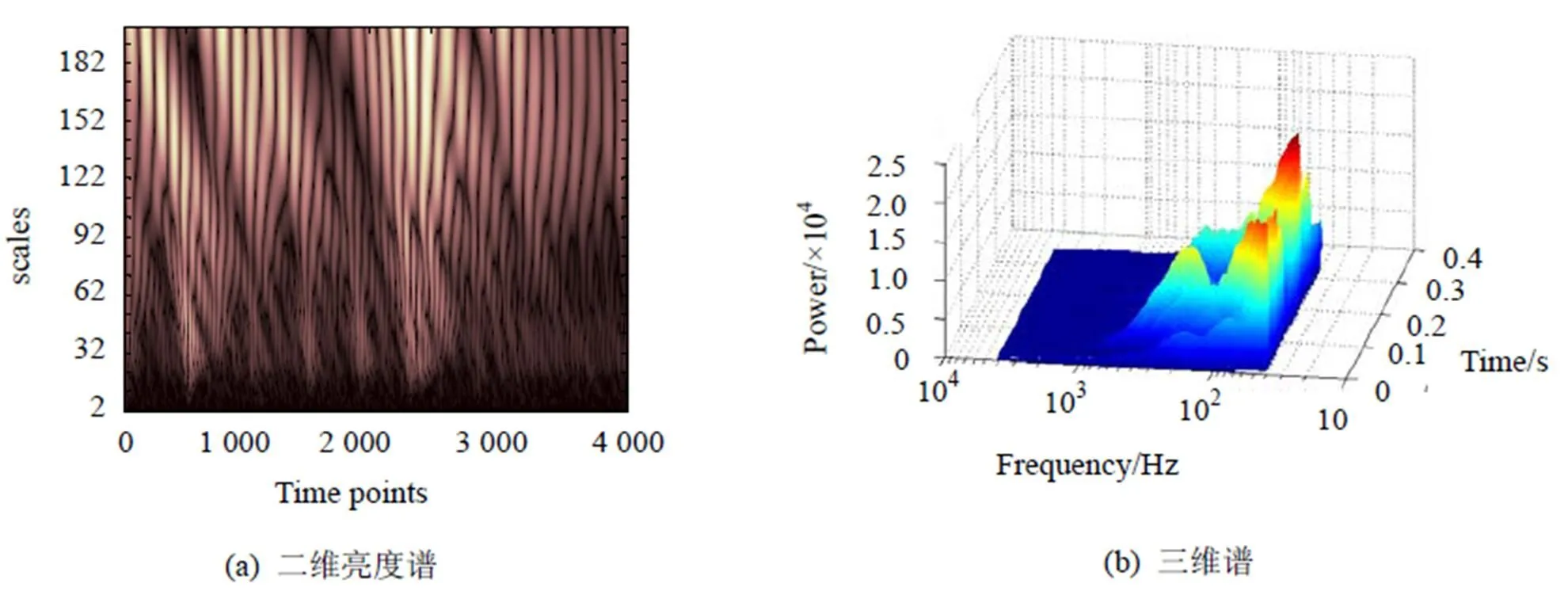
图3 大地电磁信号的小波时频图

4 MT信号的EMD分解和时频谱

EMD分解技术在时间域中表现为从小尺度到大尺度的层层滤波, 在频率域中EMD分解过程表现为从高频到低频的层层分解, 无需选择基函数, 是完全自适应于被分解的信号的. 采用EMD方法对图1所示的大地电磁信号进行分解, 图4所示为大地电磁信号的EMD分解图及其各阶对应的功率谱. 从图4中可知, 信号被自适应的分解为9层, 其中imf1为白噪声, imf2—imf8为优势子频带, residual为趋势项, 每一阶IMF分量都有不同的振幅和频率, 这为大地电磁信号的去噪等后续工作带来了方便. 整个频段内低频成分的振幅较大, 这与进行数据采集时使用仪器的低频模式采样的事实相吻合, 也说明了分解的正确性.

按照式(12)计算得到信号的Hilbert能量谱如图5所示. 从图5中可以得出: 对比图3中小波分析方法得到的时频谱图, 图3中时频谱表现的优势频率与Hilbert能量谱中表征的优势频率是一致的, 说明信号的能量主要集中在低频部分, 这与信号的实际吻合得很好. 但图5所示所示的Hilbert能量谱清晰而详细地显示了大地电磁信号能量随时频的具体分布. 与图3相比可以得到: Hilbert谱具有更好的局部化能力和更好的时频聚集性, 大地电磁数据的突变点、持续时段和频带能量分布均能够清晰地显现; HHT方法对大地电磁数据的动态变化过程刻画得比较清楚, 反应了每时段都有各自的频率特性、能量差异, 小波时频谱图难以揭示出这些细微性变化.

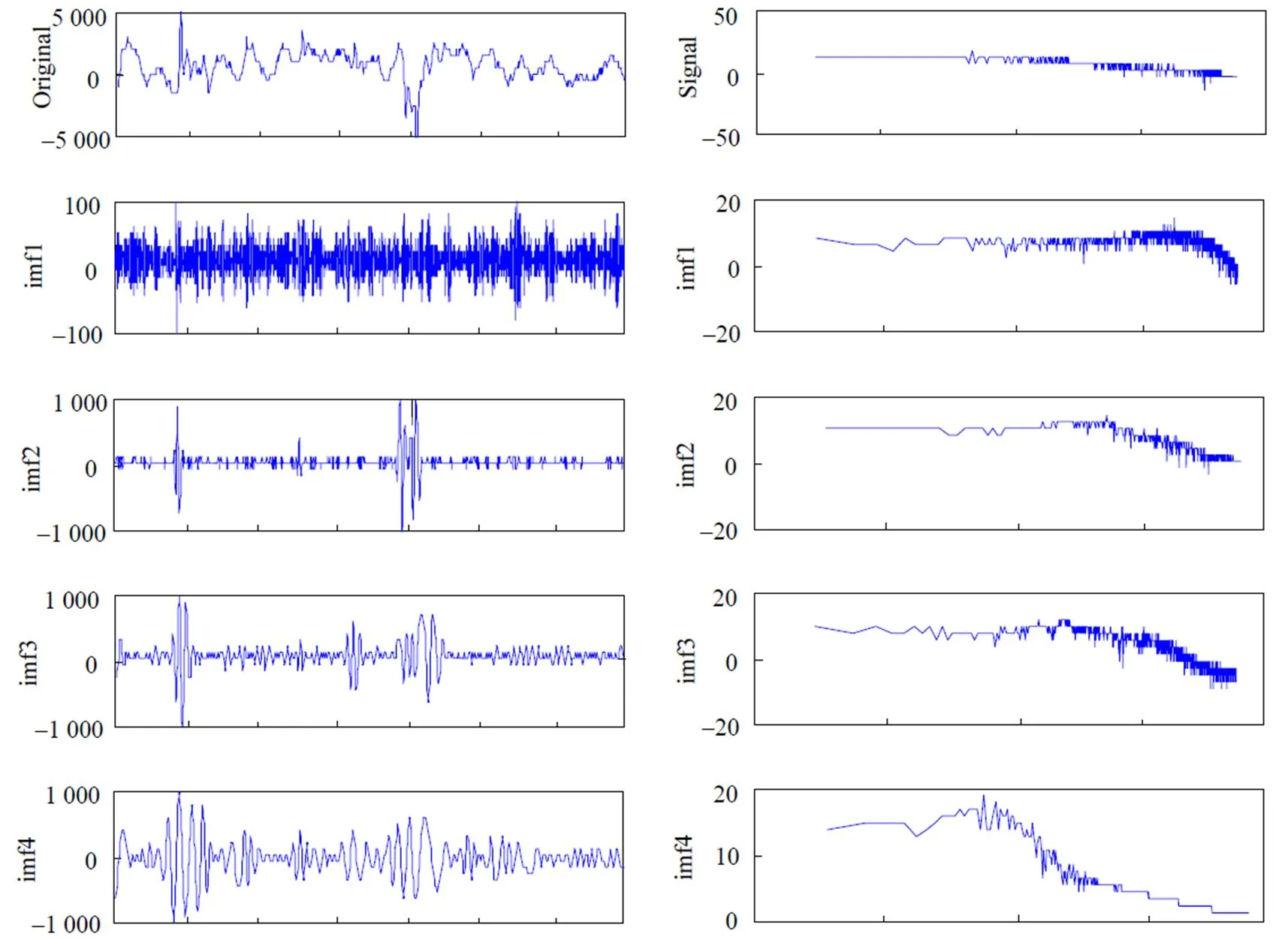
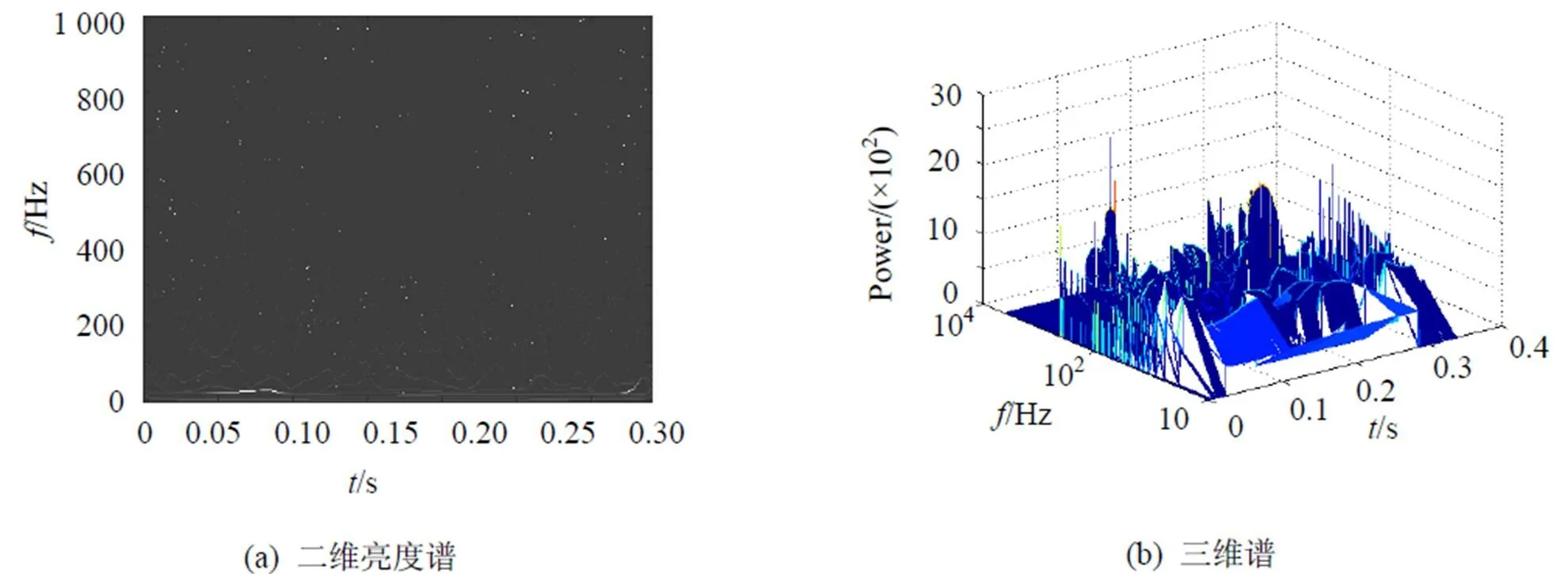
图5 大地电磁信号的Hilbert 时频谱

5 结论

小波变换是一种被广泛应用于大地电磁信号分析的方法, 它克服了短时傅里叶分析中窗口大小不随频率变化的缺点, 是一种比较理想的信号处理数学工具. 但小波谱的能量在频率范围内分布较宽, 并存在选择小波基和确定分解层数的问题. HHT方法中其EMD分解是完全自适应于信号的, 具有多分辨分析和完全重构的特性; 且取消了窗函数的作用, 具有完全的局部时频特性. Hilbert时频谱可准确描述大地电磁信号的时变特征, 能更好地揭示电磁场信号的分布规律, 是一种更精确的MT信号分析方法.

[1] 王书明, 王家映. 大地电磁信号统计特征分析[J]. 地震学报, 2004, 26(6): 669—674.

[2] 严家斌, 刘贵忠, 柳建新. 小波变换在天然电磁场信号时间序列处理中的应用[J]. 地质与勘探, 2008, 44(3): 75—78.

[3] CAI Jianhua, TANG Jingtian, HUA Xirui. An analysis method for magnetotelluric data based on the Hilbert-Huang Transform [J]. Exploration Geophysics, 2009, 40: 197—205.

[4] 汤井田, 化希瑞, 曹哲民, 等. Hilbert-Huang变换与大地电磁噪声压制[J]. 地球物理学报, 2008, 51(2): 603—610.

[5] Donoho D L. De-noising by soft-thresholding [J]. IEEE Transaction on Information Theory, 1995, 41(3):613-627.

[6] Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage [J]. J American Statist Assoc, 1995, 90: 1200—1224.

[7] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proc R Soc Lond Ser A, 1998, 454: 93—95.

[8] Huang N E, Wu M L, Long S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis [J]. Proceeding of Royal Society London A, 2003, 459: 2317—2345.

Comparison of wavelet analysis and Hilbert-Huang transform in MT signal procession

CAI JianHua1,HU WeiWen1, QING YeGui2, CHEN QinYe1

(1. Department of Physics and Electronics, Hunan University of Arts and Science, Changde 415000, China; 2. Chinese People's Liberation Army 93062 Troops, Jilin 132102, China)

Measured magnetotelluric signal is taken as the analysis object, and comparative study of wavelet analysis and Hilbert-Huang transform is applied in magnetotelluric (MT) signal procession from signal decomposition to time-frequency analysis. The mathematical theory of Wavelet analysis and Hilbert-Huang transform are expressed. The decomposition method of two ways and their physical significance for MT signal are analyzed, and the similarities and differences to characterize the spectrum of MT signal are discussed between the two methods. These provide a valuable reference foe the choice of analysis method of magnetotelluric signal procession.

magnetotelluric signal; Hilbert-Huang transform; wavelet analysis; decomposition; time-frequency analysis

P 631

1672-6146(2014)02-0029-06

10.3969/j.issn.1672-6146.2014.02.007

通讯作者email: cjh1021cjh@163.com.

2014-05-04

国家自然科学基金项目(41304098), 湖南省自然科学基金项目(12JJ4034); 湖南省教育厅青年项目(13B076); 湖南文理学院重点学科建设项目资助-无线电物理; 湖南省重点实验室“光电信息集成与光学制造技术”; “湖南省光电信息技术校企联合人才培养基地”; 常德市科技局博士创新创业项目(2013BS01); 常德市科技局项目(2011JC02).

(责任编校:刘刚毅)