金属钨中氦团簇扩散与形核特性的分子动力学研究
周 芬, 邓辉球
金属钨中氦团簇扩散与形核特性的分子动力学研究
周 芬, 邓辉球*
(湖南大学 应用物理系, 湖南 长沙, 410082)
本文应用分子动力学方法模拟研究了氦团簇在金属钨中的扩散特性, 得到了不同大小团簇的扩散系数, 结果表明氦团簇越大, 扩散越慢. 氦团簇越大越容易激发出自间隙钨原子, 且大的氦团簇只需要很低的钨基体温度即可激发. 在金属钨中加入125个氦原子(氦浓度低于0.1%), 研究了氦团簇的形核特性. 通过比较氦团簇、自间隙团簇和空位团簇3种缺陷的尺寸分布发现, 氦团簇的尺寸在800 K达到最大值, 其它两种缺陷尺寸随温度的增加而逐渐增大.
氦团簇; 扩散; 形核; 分子动力学模拟
金属钨因其高熔点、高导电率和低溅射等属性[1]被候选为核聚变托卡马克装置中最有可能全面使用的第一壁面对等离子体材料(PFM). 聚变产物氦在金属中具有极低的溶解度, 且很容易被空位、晶界和位错等缺陷捕获从而导致氦原子的聚集. 当氦原子聚集到一定程度时, 将形成氦团簇和氦泡, 使材料中出现肿胀和孔洞, 导致材料的力学性能降低并失效. 最近实验发现氦离子辐照能使钨表面出现纳米丝状结构[2], 将改变钨PFM表面的物理和化学性质. 丝状结构层在表面容易脱落, 导致更多钨杂质或灰尘的形成[3], 进而影响等离子体的稳定运行. 因此研究氦在钨中的扩散与形核行为具有重要意义.
目前对钨中氦的行为已经进行了很多方面的研究, 特别是对氦扩散行为的研究. 第一性原理方法研究了单个氦在钨中的扩散性质, 发现单个氦原子沿四面体-四面体和四面体-八面体-四面体路径的扩散势垒分别为0.06 eV和0.23 eV[4—5], 这与实验值0.23~0.32 eV[6—7]存在一定的差异. Becquart和Domain[8]指出单个氦原子在扩散的时候很容易与周围的缺陷相结合, 导致计算的扩散势垒并不是单个氦原子的. 此外, 研究者们还利用分子动力学方法研究了单个氦和氦团簇在钨中的扩散势垒和扩散路径[9—12]. 同时Juslin等人研究了氦泡在钨中的初步形核, 发现除了包含1~3个空位的小团簇外, 氦与氦团簇或者氦-空位团簇的结合能都是与团簇的大小密切相关[13]. 但是目前对于氦团簇在钨中的成核过程以及温度效应的研究还不深入. 为此, 本文模拟研究了氦团簇在钨中的扩散、自间隙原子的激发以及不同温度下氦在钨中的形核特性.
1 计算模型与模拟方法
分子动力学是计算机模拟中的一种重要方法. 它主要利用牛顿力学来模拟原子和分子体系的运动, 并预测材料的物理性质和微观结构的演变, 因此得到广泛的应用. 在模拟过程中原子间相互作用势函数的选取至关重要. 对于钨-钨、钨-氦原子间相互作用, 本文采用Jusin等人建立的多项式形式的势函数来描述[13], 氦-氦之间的作用则采用的是Beck构建的相互作用势函数[14].
针对不同情况, 本文应用三维周期性边界条件构建了两个钨块体模型. 对于氦原子和团簇在钨中的扩散情况, 采用100× 100× 100的盒子大小(包含2000个钨原子); 其中0为金属钨块体的晶格常数, 大小为3.165 2× 10-10m. 模拟氦在钨中的形核过程时, 则采用450× 450× 450(包含182 250个钨原子), 并将125个氦原子均匀分布在整个钨块体中. 应用分子动力学方法, 在不同的温度下对钨-氦体系进行弛豫, 每个时间步长为10-15s, 并利用速度标定法对整个体系进行控温. 当整个体系达到平衡后, 统计缺陷种类和数目.
在给定的温度下, 通过跟踪氦团簇的质心位置, 得到氦团簇扩散的均方位移 (MSD)曲线. 通过对MSD曲线进行处理, 可得到扩散系数. 再对Arrheius方程=0exp(-E/B)两边取对数可知, Ln和1/之间存在线性关系, 通过拟合该直线, 由直线的斜率和截距就能分别求出扩散激活能和扩散前因子.
2 结果与讨论
2.1 金属钨中氦原子和氦团簇的扩散特性
具有满电子排布的氦原子具有惰性, 几乎不与钨原子发生直接相互作用, 在金属钨基体中极易扩散(扩散势垒非常低). 多个氦原子则倾向于聚集在一起, 形成氦团簇, 并长大成氦泡. 在本文中我们应用分子动力学首先研究了氦原子和氦团簇的扩散特性. 图1中给出了400~800 K下, 氦原子和氦团簇扩散系数()的对数和系统温度()的倒数之间的关系. 从图1中可以发现Ln和1/近似地满足线性关系, 而且温度越低, 氦团簇的扩散系数也越低. 根据Arrheius拟合得到氦原子和氦团簇的扩散势垒与扩散前因子都列于表1之中. 通过比较不同大小的氦团簇的扩散系数可知, 当氦原子与另一个氦原子或氦团簇结合时, 其可移动性将降低. 这与Li[11]和Zhou[12]等人的模拟结果相同, 只是我们模拟计算出来的氦团簇的扩散势垒稍微偏高, 这与势函数的选取有一定的关系.
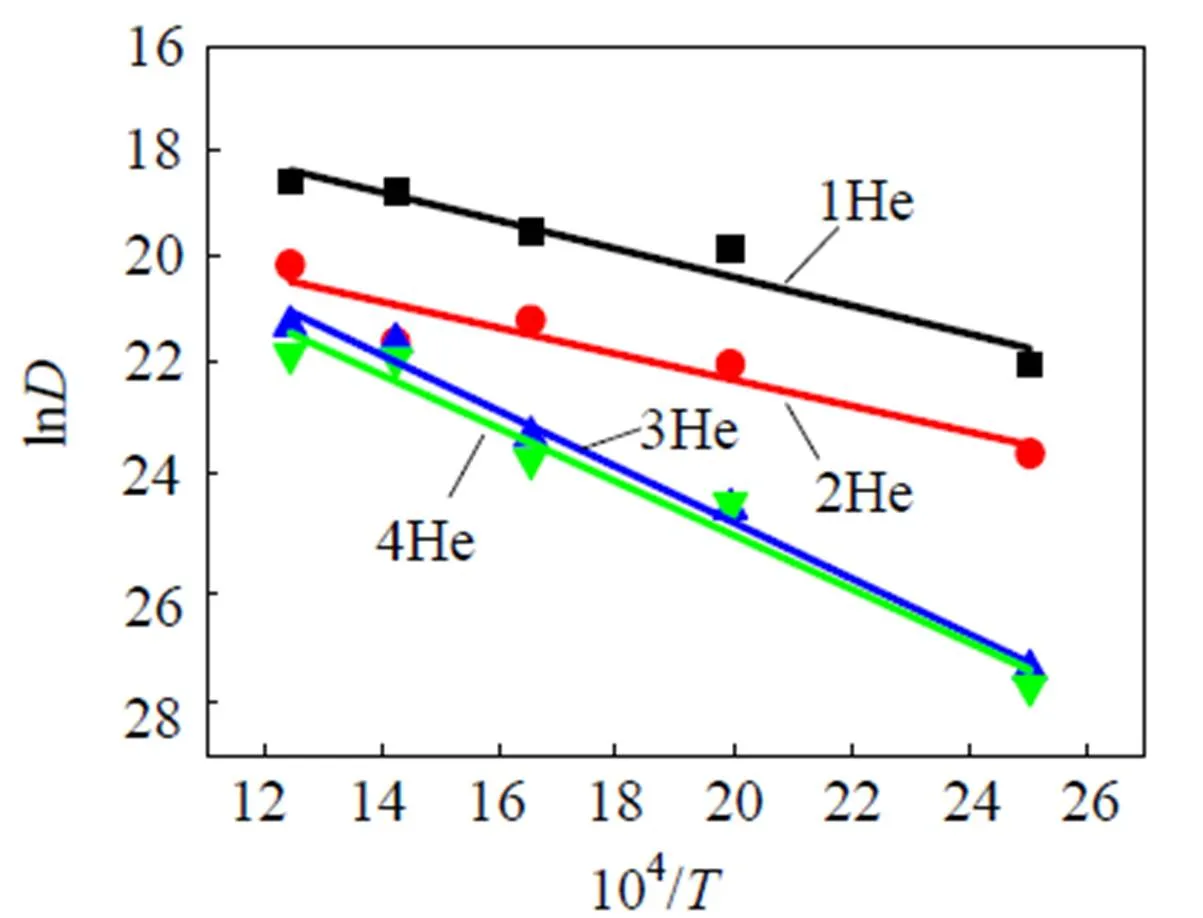
图1 氦和氦团簇扩散的LnD-1/T曲线, 温度范围为400~800 K.
表1 氦和氦团簇在金属钨中的扩散势垒和扩散前因子

(续表1)
2.2 氦团簇激发自间隙钨原子的特性
在金属钨基体中, 多个氦原子聚集, 易形成氦团簇, 并激发出自间隙钨原子. 本文通过模拟得到了一个He(= 3~7)团簇在钨块体中激发自间隙钨原子所需要的最低温度. 如图2所示, 氦团簇越大, 激发出自间隙钨原子所需要的温度就越低. 当氦团簇包含的氦原子数小于5时, 需要在700 K以上的温度下才能观察到自间隙原子的激发现象. 对于含3个氦原子的团簇, 激发自间隙原子所需要的温度高达1 200 K. 当氦团簇中包含的氦原子数增多时, 激发自间隙原子所需要的温度迅速降低. 当团簇中包含的氦原子数目大于7时, 甚至在温度低于100 K的情况下都能发射自间隙原子. 一旦晶格钨原子被踢出形成自间隙原子并留下一个空位时, 氦团簇与空位结合为氦团簇-空位复合体, 此时氦原子被钉扎在空位的周围, 围绕着空位不停的旋转, 并且在旋转过程中保持团簇的质心不变. 因此氦团簇-空位复合体主要依靠吸附周围游离的氦原子或者小的氦团簇来长大.
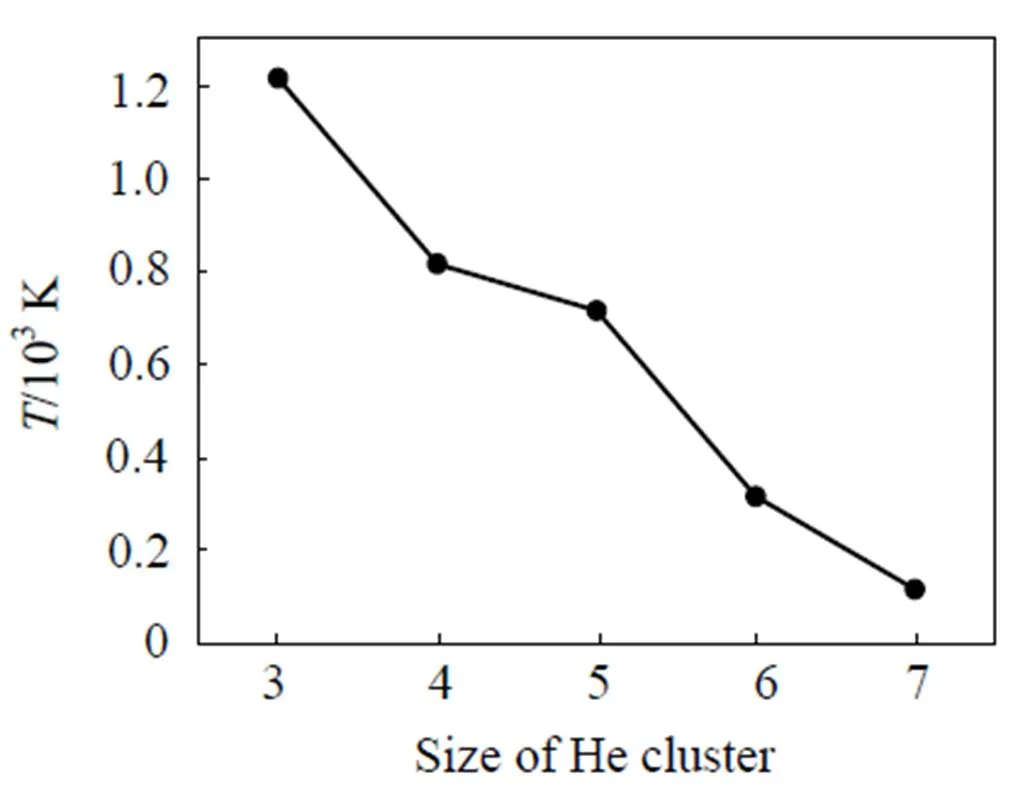
图2 Hen(n = 3~7)团簇激发自间隙所需要的最低温度.
2.3 金属钨中氦团簇的形核特性
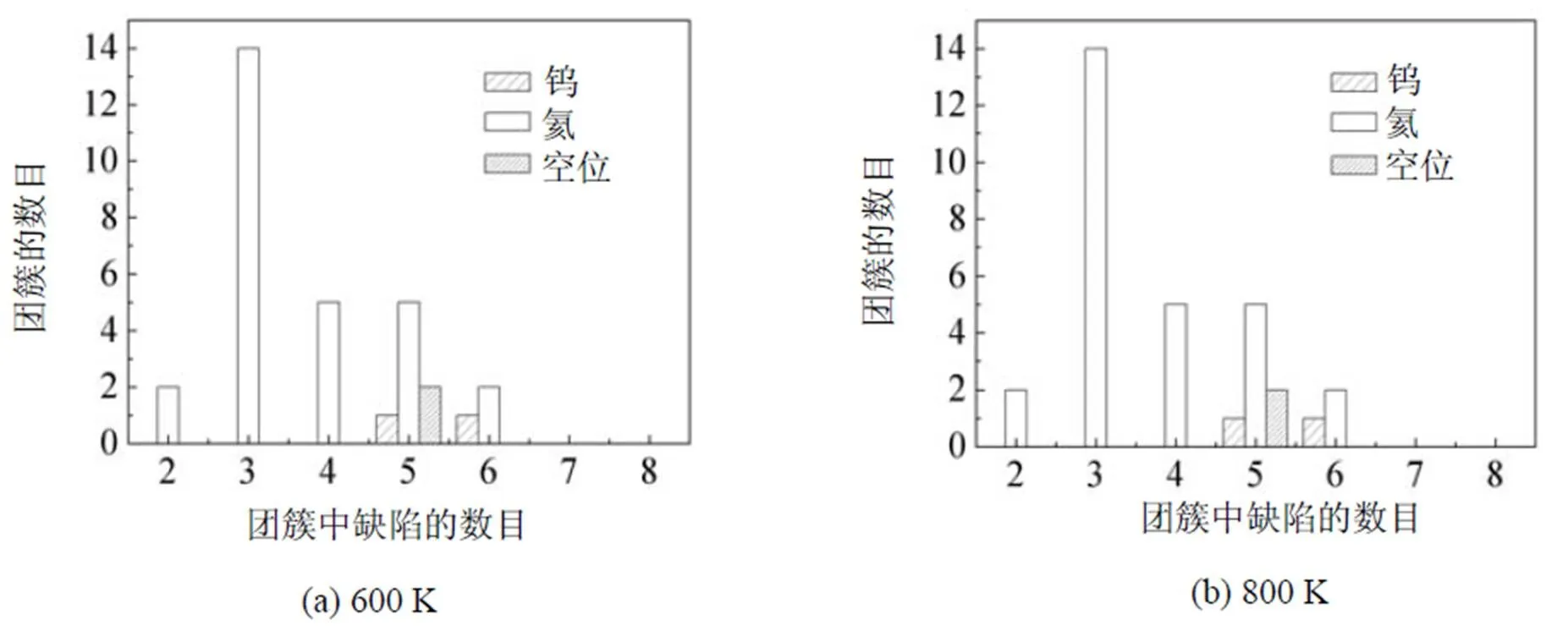
由于具有非常低的扩散势垒, 氦原子在金属钨基体中极易扩散. 为研究金属钨基体中的氦团簇形核特性, 本文研究了氦浓度非常低的钨-氦体系. 我们在一个很大的金属钨块体中, 初始均匀分布125个氦原子, 此时氦原子的浓度低于千分之一. 在温度为600~1 200 K之间, 应用分子动力学分别弛豫钨–氦体系3.7 ns之后, 发现在钨-氦体系中所形成的氦团簇、空位团簇以及氦-空位复合体等缺陷数目均达到动态平衡. 各种缺陷在整个钨-氦体系中的分布情况(图3), 其中半径小的小球代表氦原子, 半径大的浅色小球代表自间隙钨原子, 深色小球代表空位. 自间隙钨原子形成了沿<111>方向排列的挤列子, 基本上全都附着在氦-空位团簇复合体附近. 体系中仅存在极少量游离的单个氦原子, 在钨基体中快速扩散. 如果模拟时间足够长, 这些游离的氦原子也将与其它大的氦团簇结合, 形成更大的氦团簇, 进一步长大形成氦泡. 为了考察温度对氦泡形核的影响, 本文也研究并统计了不同温度下钨-氦体系中缺陷的大小和数目分布情况(图4). 在800 K下, 发现氦团簇的尺寸比其它温度下的大很多, 而其它温度下氦团簇的最大尺寸则相近. 当温度低于1 000 K时, 氦(He)团簇的尺寸是3种缺陷团簇中最大的; 然而自间隙钨原子(SIA)团簇和空位(V)团簇的尺寸都随温度升高而迅速增加, 并逐渐超过氦团簇最大尺寸. 由此可见温度对空位和自间隙团簇的影响明显大于对氦团簇的影响, 其中可能的原因是温度的升高在促进了氦团簇扩散的同时也增加了氦与氦-空位团簇的解离.
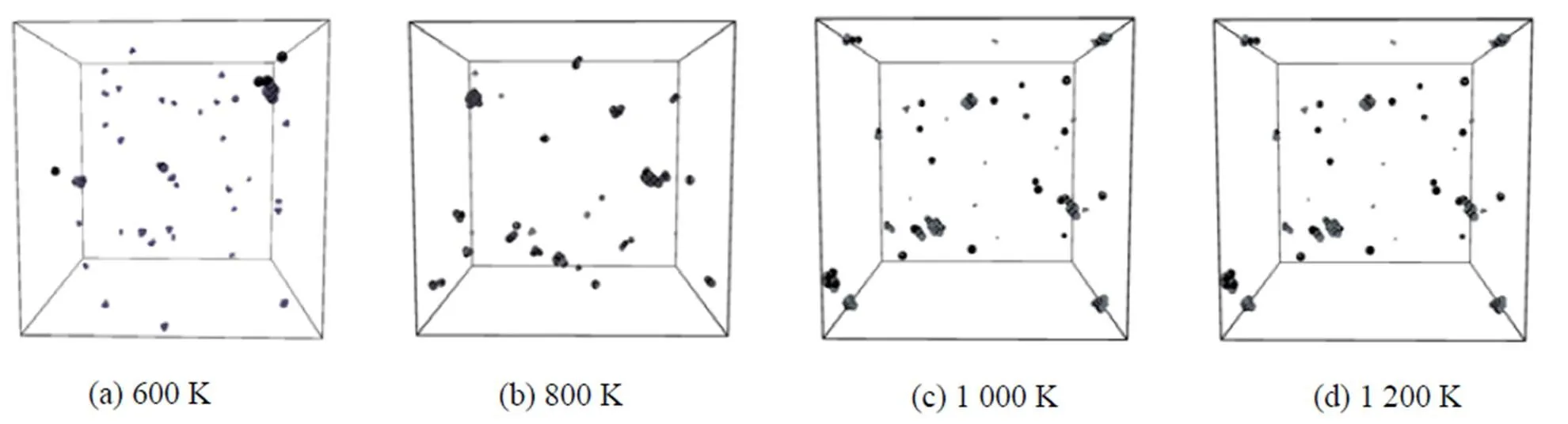
图3 3.7 ns时氦、空位和自间隙钨原子3种缺陷团簇在钨基体中的分布情况
3 结论
本文用分子动力学方法研究了氦在金属钨中的扩散和形核特性. 模拟研究发现, 单个氦原子在金属钨中的扩散势垒很低, 随着氦团簇的增大, 其扩散势垒增加, 移动性逐渐降低. 当氦团簇的尺寸达到一定大小时, 会激发自间隙钨原子, 形成氦团簇-空位复合体, 并被空位钉扎. 不同大小氦团簇激发自间隙原子所需要的最低温度不一样. 氦团簇越大越容易激发出自间隙钨原子, 且只需要很低的温度, 而小的氦团簇只有在温度很高时才能激发自间隙钨原子. 氦团簇则依靠吸收周围扩散过来的氦原子或氦团簇进一步长大. 温度能够在一定范围内促进氦泡的形核, 空位和自间隙原子团簇随温度的增高而增大.
[1] Lee H T, Haasz A A, Davis J W, et al. Hydrogen and helium trapping in tungsten under single and sequential irradiations [J]. Journal of Nuclear Materials, 2007, 360: 196.
[2] Yajima M, M Yamagiwa M, Kajita S, et al. Comparison of damages on tungsten surface exposed to noble gas plasmas [J]. Plasma Science and Technology, 2013, 15: 282.
[3] M Yamagiwa, S Kajita, N Ohno et al. Helium bubble formation on tungsten in dependence of fabrication method [J]. Journal of Nuclear Materials, 2011, 417: 499.
[4] Zhou H B, Liu Y L, Jin S, et al. Towards suppressing H blistering by investigating the physical origin of the H-He interaction in W [J]. Nuclear Fusion, 2010, 50: 115010.
[5] Aziz R A, Janzen A R, Moldover M R. Ab in calculation for helium: A standard for transport property measurements [J]. Physical Review Letters, 1995, 74: 1586.
[6] Amano J, Seidman D N. Diffusivity of3He atoms in perfect tungsten crystals [J]. Journal of Applied Physics, 1984, 56: 983.
[7] Wagner A, Seidman D N. Range profiles of 300- and 475-eV4He+ions and diffusivity of4He in tungsten [J]. Physical Review Letters, 1979, 42: 515.
[8] Becquart C S, Domain C. Migration energy of He in W revisited by ab into calculations [J]. Physical Review Letters, 2006, 97: 196402.
[9] Li X C, Shu X L, Liu Y N, et al. Analytical W-He and H-He interatomic potentials for a W-H-He system [J]. Journal of Nuclear Materials, 2012, 426: 31.
[10] Wang J, Zhou Y L, Li M, et al. Atomistic simulations of helium behavior in tungsten crystals [J]. Journal of Nuclear Materials, 2012, 427: 290.
[11] Zhou Y L, Wang J, Hou Q, et al. Molecular dynamics simulations of the diffusion and coalescence of helium in tungsten [J]. Journal of Nuclear Materials, 2014, 446: 49.
[12] Juslin N, Wirth B D. Interatomic potentials for simulation of He bubble formation in W [J]. Journal of Nuclear Materials, 2013, 432: 61.
[13] Beck D E. A new interatomic potential function for helium [J]. Molecular Physics, 1968, 14: 311.
The diffusion and nucleation characteristics of helium clusters in tungsten by molecular dynamics simulation
ZHOU Fen, DENG HuiQiu
(Departmentof AppliedPhysics, Hunan University, Changsha 410082, China)
The diffusion and nucleation characteristics of helium clusters in tungsten were studied by molecular dynamics simulation. The diffusion coefficients of different sizes of helium clusters were obtained. The results showed that the bigger helium cluster is, the slower it migrates and the easier for it to kick out a self-interstitial tungsten atom. When the helium cluster is large enough, it can push a tungsten atom away from its lattice, even at a very low temperature. 125 helium atoms were planted into the tungsten host and then the nucleation mechanisms of helium clusters were studied with molecular dynamics simulation. It can be concluded that the size of helium clusters achieved its peak value at 800 K; however, the other two defect clusters (self-interstitial atoms and vacancy clusters) increase with the increase of temperature.
helium clusters; diffusion; nucleation; molecular dynamics simulation
TG 113.25
1672-6146(2014)02-0047-05
10.3969/j.issn.1672-6146.2014.02.010
通讯作者email: hqdeng@hnu.edu.cn.
email: S12072011@hnu.edu.cn.
2014-05-13
国家自然科学基金(51371080)
(责任编校:刘刚毅)

