以行业分类为基础的期权定价与实证分析
贾斯莹
(天津大学经济与管理学部,天津 300072)
以行业分类为基础的期权定价与实证分析
贾斯莹
(天津大学经济与管理学部,天津 300072)
首先对布莱克-斯科尔斯期权定价模型和二叉树期权定价模型进行阐述、解析和比较,然后将理论应用于实践,以3个不同行业的9个公司的期权价格为例对2种期权定价方法进行实证检验。最后得出这2种模型的估计效果与哪些因素有关的结论以及它们在不同行业的适用性。
期权定价;Black-Scholes模型;二叉树模型
一、研究动机
金融理论是金融创新的源泉。期权理论之所以能够付诸于实践是因为2个大致同时发生的重要变化:自20世纪50年代以来,金融的学术研究从地位低的、以描述性活动为主的研究,逐渐向地位高的、分析性的、以数学为基础的科学研究转变;大量复杂的关于金融衍生品的数学性分析得以发展[1]。
1973年,布莱克和斯科尔斯提出了Black-Scholes期权定价模型(B--S模型),对标的资产的价格服从对数正态分布的期权进行定价。该模型可以在很短的时间内计算大量的期权价格。但其同样也存在局限性,主要有忽略了交易成本、波动率不可观测且为随机变量、不适用于随机利率、不允许标的资产价格过程的随机跳跃、不能用于准确的美式期权定价等[25]。
1979年,由Cox、Ross和Rubinstein首次提出二叉树模型。该模型与B--S模型相比最大的优势是它可以准确地为美式期权定价,如美式看跌期权。该模型的主要限制表现在以下2个方面。①这种用来计算偏导数的树方法可能会因为二项式离散化的本质而变得无效;②它假设资产价格在下一个时段内只会有2种可能的变动,但是现实情况往往并非如此[69]。
B--S模型和二叉树模型是两种被广泛应用的期权定价模型,很多学者对它们进行过分析比较,但大多是从公式推导的角度或选用某个公司的数据进行研究。本研究拟用美国银行公司、摩根大通公司、花旗集团;通用汽车公司、福特汽车公司、浙江康迪车业有限公司;谷歌公司、雅虎公司、亚马逊公司这几个在银行、汽车制造和互联网等不同行业中有代表性的公司的期权数据对以上2种期权定价方法进行实证分析,以研究上述2种期权定价模型在不同行业中的适用性及其特点。
二、模型概述
1.B--S模型
通过设定一些严格的假设并使用无套利定价方法,模型计算出了一份以不分红的股票为标的资产的看涨期权的理论价格。
该模型的3个假设:①假设标的资产价格可以为任意大的正值;②假设短期利率在期权期限内保持不变;③假设标的资产价格波动率在期权期限内不变。
模型定价公式如式(1):
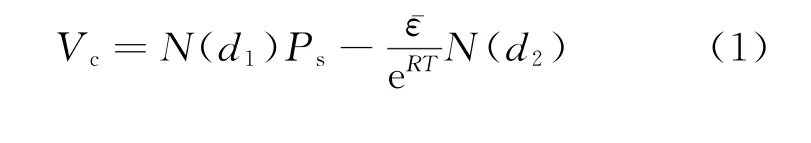
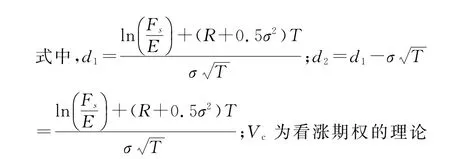
价值;Ps为当前股票价格;E为执行价格;R为连续复利计算的无风险利率;T为期权的剩余期限; σ为股票连续复利年收益率的标准差;N(x)为标准正态分布变量的累积概率分布函数(即这个变量小于x的概率);ln为自然对数函数;e为自然对数的底(2.718 28)。
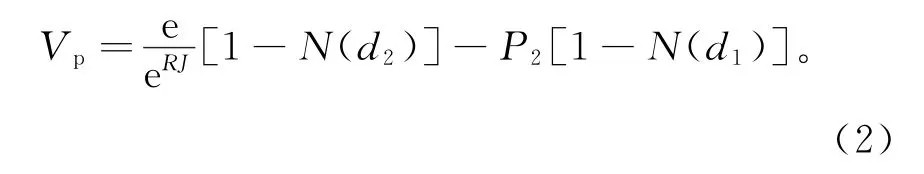
2.二叉树期权定价模型
二叉树期权定价模型假设标的资产未来价格的变动仅存在2种可能:上涨或者下跌,投资者可以利用货币市场与股票市场复制出收益变动情况与期权完全相同的投资组合,因而他们的价格也应该完全相同。设:S0为股票的即期价格,u为股价的上升因子(即若股价上涨,股票的期末价格为S0u),d为股价的下降因子(即若股价下跌,股票的期末价格为S0d),r为无风险利率,C0为看涨期权的即期价格,C(ST)为期权在T时刻的收益,则二叉树期权定价模型的公式如式(3):
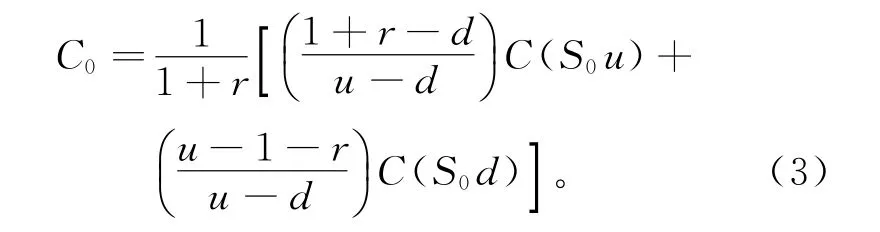
式(3)是单时段二叉树模型,若改为多时段模型该公式依然适用。为了保证股票年收益率的标准差不变,模型按照如下公式调整上升与下降因子:
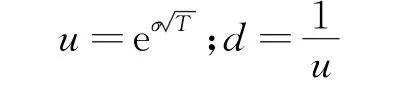
式中,σ为股票价格的波动率;T为期权的期限。
多时段模型的计算步骤与单时段模型相似。首先确定最后一期的期权价格,然后根据最后一期的期权价格,使用单时段模型的公式计算出其前一期的期权价格,以此类推,最后计算出看涨期权的期权现值。这样得出的二叉树期权定价模型的一般化公式为:
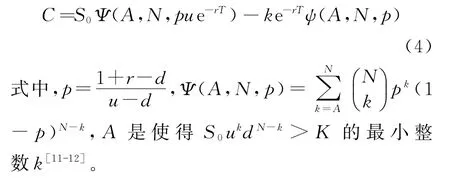
3.B-S模型和二叉树期权定价模型的关系
2种模型可以相互补充。随着对期权期限的不断细分,划分的时段数不断增加,二叉树期权定价模型的分布函数就越来越趋向于正态分布的分布函数,二叉树模型和B—S模型的结果相一致。
三、实证研究
利用2014年3月1日的摩根大通公司、福特汽车公司和雅虎公司的期权数据对以上2个期权定价模型进行实证研究。无风险利率0.58%,期权的剩余期限21天。
运用计量经济学软件EViews 6.0,将本研究计算所得的B--S模型价格与二叉树期权定价模型价格进行OLS回归。
1.公司股票特征值
所选各公司的股票数据见表1。
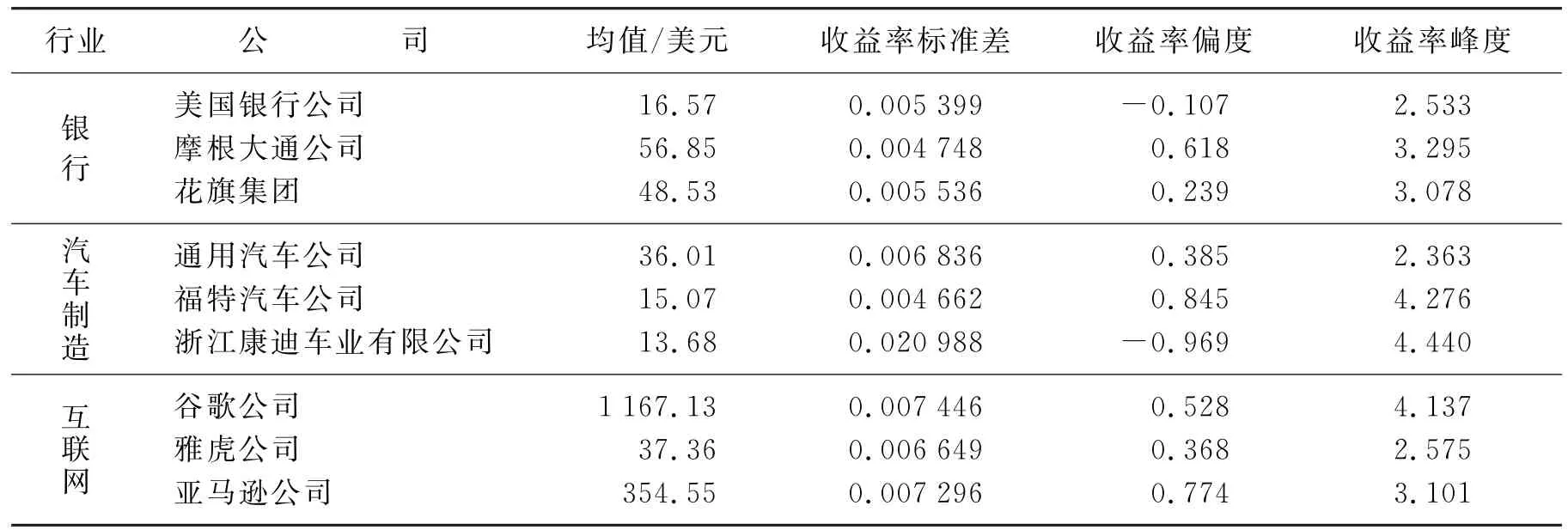
表1 股票数据
从表1可以看出,除美国银行公司、浙江康迪——车业有限公司的收益率是负偏斜以外,其余公司的收益率都是正偏斜;各公司的峰度值波动较大,该值越接近3,说明变量值的次数分布越接近正态分布。一般当峰度接近于1.8时,分布曲线呈水平矩形分布形态。结合表1和表2可知,公司股价的偏斜程度越小、峰度值越远离3,二叉树模型相对于B-S模型的优势越明显,相对准确度越高。
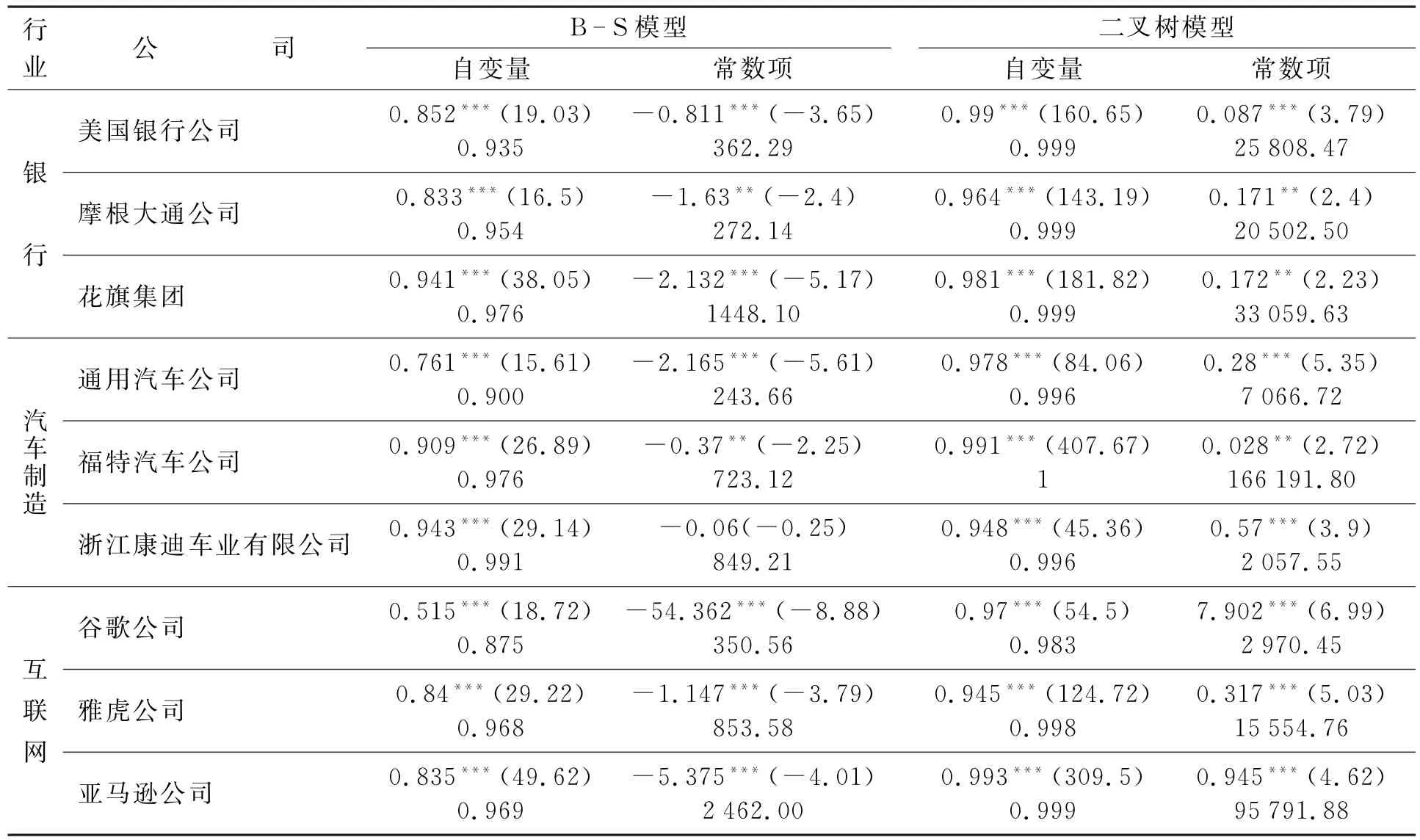
表2 看涨期权
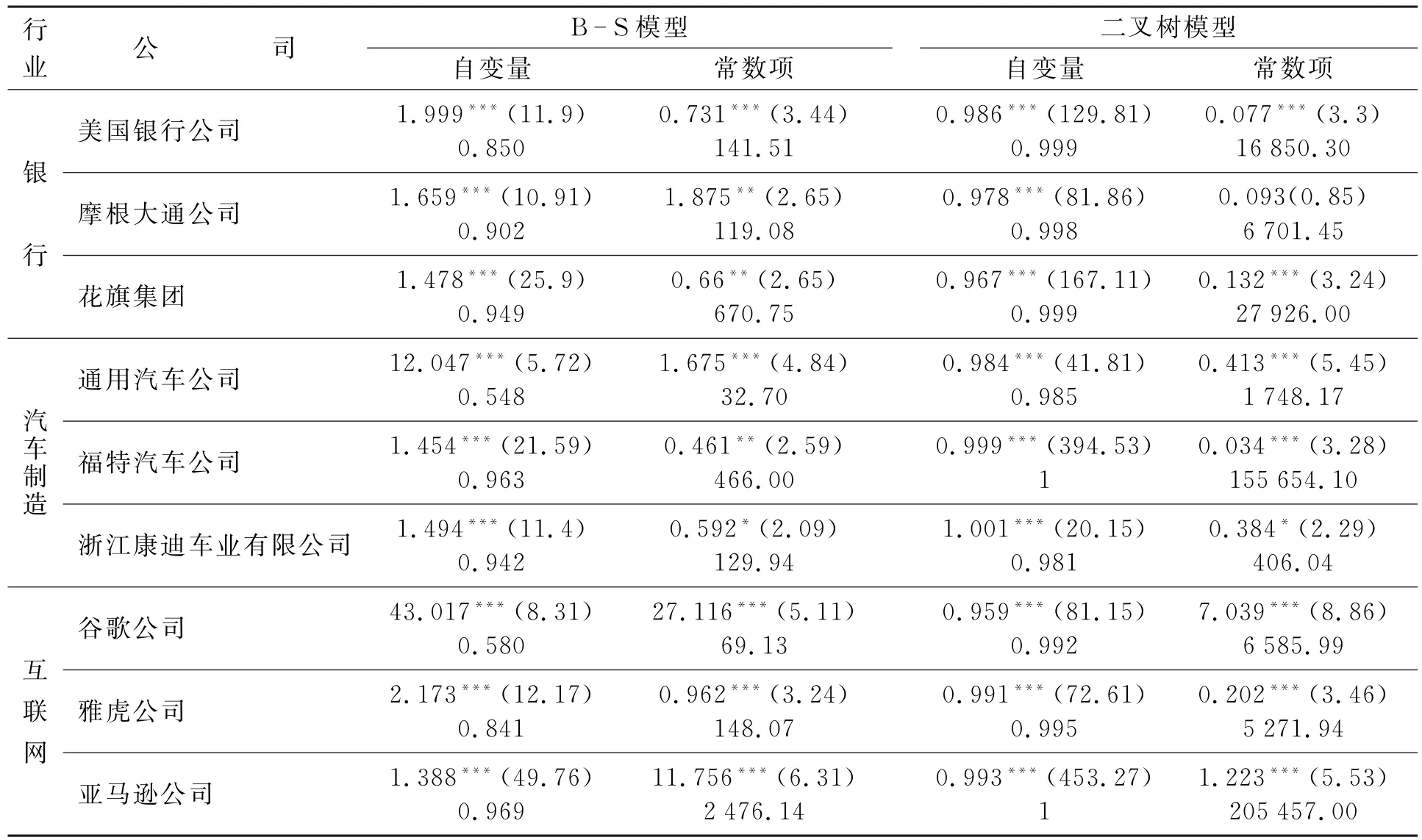
表3 看跌期权
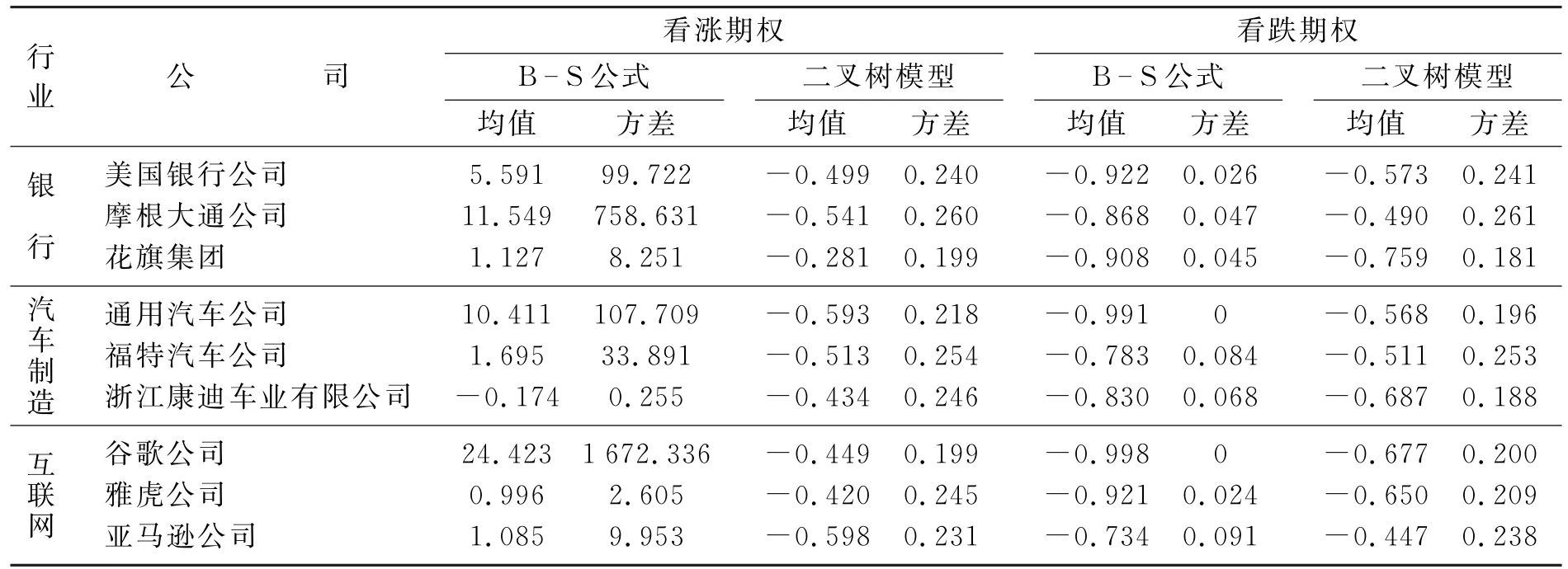
表4 公司期权价格偏差(理论值--实际值)/实际值
2.计算期权价格的几点说明
(1)采用对数差分的方法来计算样本股票日收益率,其计算公式为Rt=ln Pt-ln Pt-1,其中Pt是Pt-1的后一日收盘价。这样一方面可以使数据更加平滑,克服数据本身的异方差;另一方面能够达到价格的对称性。
(2)采用历史波动率来计算期权价格。如前所述,模型有高估期权价格的现象,可能是因为波动率取前面一个月的历史波动率,历史波动率反应的是过去股价变化的情况,并不一定符合将来的实际情况。
(3)以上二叉树期权定价方法均采用5个时段进行期权定价。不断地增加时段数,可以使误差不断减小。
3.公司期权价格拟合图
摩根大通公司的期权价格曲线如图1所示。
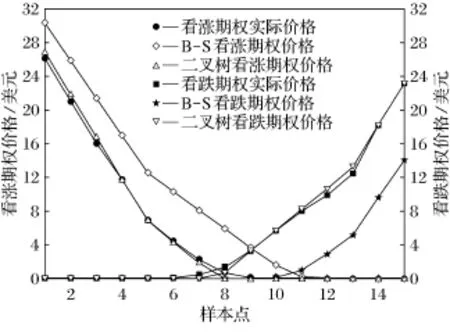
图1 摩根大通公司期权价格走势图
福特汽车公司的期权价格曲线如图2所示。
雅虎公司的期权价格曲线如图3所示。
4.期权价格相关数据
据表4所示,对于看涨期权,B- S模型一般会高估价格。有研究发现这个现象与随机波动率有关,且价格高估的程度随到期时间的增加而增大[13]。随着执行价格的增加,价格偏差先升后降;二叉树模型则会低估价格,随着执行价格的增加价格偏差一直稳定在较小的数值。二叉树模型的偏差均值和方差都显著小于B—S模型的数值。而对于看跌期权,两者都低估了其价格,价格偏误总体来看呈下降趋势,且二叉树模型的理论价格能更快地回归到实际价格。B- S模型价格偏差的方差始终小于二叉树模型的对应数值。
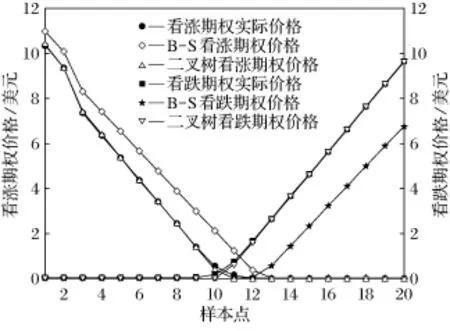
图2 福特汽车公司期权价格走势图
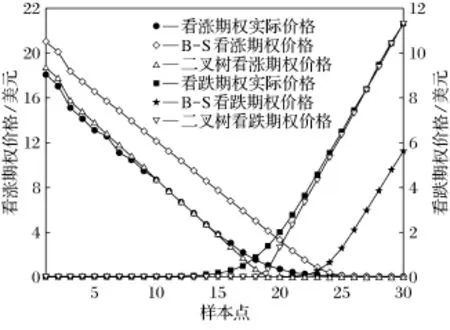
图3 雅虎公司期权价格走势图
从表2~表4中可以看出,整体来说,二叉树模型的拟合效果优于B- S模型。对于银行业来说,估计看涨期权时,二叉树模型的偏差均值和方差都较小,拟合效果更好;估计看跌期权时,二叉树模型的估计精度也略大于B- S模型。对于汽车制造业来说,二叉树模型对看涨期权价格的估计效果更好,但也存在例外,如B- S模型对浙江康迪车业有限公司期权价格的偏差均值更小,拟合效果也差不多;在对看跌期权进行估计时,则要具体问题具体分析。对于互联网行业来说,B- S模型对看涨期权的估计偏差最明显,拟合优度也有所下降;而估计看跌期权时,B- S模型的拟合效果与二叉树模型相比很不理想,所以B- S模型不适合估计该行业的看跌期权。对于股价较低,波动率较小的公司而言,2种模型对看涨期权价格的估计效果相近;而当公司股价和波动率都很大时,如谷歌公司,二叉树模型的估计效果则明显占优。
四、结 论
J.A.Campbell曾指出,如果在期权期限内没有股利的发放,B- S模型可以为美式看涨期权定价[14]。但通过实证研究发现,在某种特定的条件下,B- S模型也能够为看跌期权提供比较可信的价格。
从实证结果来看,二叉树模型的估计精度更高,而B- S模型适合为股票价格不过千、波动率较低的看涨期权及收益率的偏度在±0.4以上、峰度在2.6~3.4之间的看跌期权进行定价。由上述各行业之间的比较可以看出,在银行业的期权定价中,两种模型的估计效果都很好,且在公司股价收益率的偏度值和峰度值都适合的条件下,可以利用B- S模型为看跌期权定价;在汽车制造业的期权定价中,二叉树方法的优势更加明显,但B- S模型依然可以很好地为看涨期权和具备一定特征的看跌期权定价;在互联网行业中,由于公司的股价及其波动率可能较大,此时使用二叉树模型估计看涨期权价格比B- S模型更准确,并且该行业一般不适用B- S模型估计看跌期权价格。
[1]Mac Kenzie D.Is Economics Performative?Option Theory and the Construction of Derivatives Markets[J].Journal of the History of Economic Thought,2006,28(1):29 -55.
[2]Bakshi G,Cao C,Chen Z.Pricing and Hedging Long-Term Options[J].Journal of Econometrics,2000,94(1/ 2):277-318.
[3]Company R,Navarro E,Ramón Pintos J,et al. Numerical Solution of Linear and Nonlinear Black-Scholes Option Pricing Equations[J].Computers&Mathematics with Applications,2008,56(3):813- 821.
[4]Smith P,Gronewoller P,Rose L C.Pricing Efficiency on the New Zealand Futures and Options Exchange[J]. Journal of Multinational Financial Management,1998,8 (1):49- 62.
[5]Jackwerth J C.Option-Implied Risk-Neutral Distributions and Implied Binomial Trees:A Literature Review[J]. The Journal of Derivatives,1999,7(2):66- 82.
[6]Pelsser A,Vorst T C F.The Binomial Model and the Greeks[J].The Journal of Derivatives,1994,1(3):45 -49.
[7]Chung S L,Shackleton M.The Binomial Black–Scholes Model and the Greeks[J].Journal of Futures Markets, 2002,22(2):143- 153.
[8]Lo K H,Wang K,Hsu M F.Pricing American Asian Options with Higher Moments in the Underlying Distribution[J].Journal of Computational and Applied Mathematics,2009,223(1):304- 313.
[9]Rubinstein M.Edgeworth Binomial Trees[J].The Journal of Derivatives,1998,5(3):20- 27.
[10]类承曜.固定收益证券[M].第3版.北京:中国人民大学出版社,2013.
[11] 邱宝环.两种期权定价模型在金融衍生产品中应用与比较[J].金融经济,2010(24):112- 113.
[12]王江.金融经济学[M].北京:中国人民大学出版社,2006.
[13]Hull J,White A.The Pricing of Options on Assets with Stochastic Volatilities[J].The Journal of Finance,1987, 42(2):281- 300.
[14]Campbell J A.Real Options Analysis of the Timing of IS Investment Decisions[J].Information&Management, 2002,39(5):337-344.
【责任编辑 孙 立】
Option Pricing Based on Industry Classification and Empirical Analysis
Jia Siying
(College of Management&Economics,Tianjin University,Tianjin 300072,China)
Black-Scholes option pricing model and the binomial tree option pricing model are described,analyzed and compared.Applying the theories to the practice,using the option prices of nine companies in three industries as an example,the two kinds of option pricing method is tested. The conclusion of what factors contributing to the estimate effect of these two models is given,as well as their applicability in different industries.
option pricing;Black-Scholes model;binomial tree model
F 831.5
A
2095-5464(2014)04-0469-05
2014--02--24
天津大学2013年大学生创新创业训练计划(201310056215)。
贾斯莹(1993--),女,辽宁沈阳人,天津大学本科生。

