The New Doppler Shift-and-Range Positioning Algorithm for the Global Navigation Satellite System

Ji Haifu，Ma Lihua，Ai Guoxiang，Wang Meng

(1.National Astronomical Observatories，Chinese Academy of Sciences，Beijing 100012，China；2.University of the Chinese Academy of Sciences，Beijing 100049，China)

The New Doppler Shift-and-Range Positioning Algorithm for the Global Navigation Satellite System

Ji Haifu1，2，Ma Lihua1，Ai Guoxiang1，Wang Meng1

(1.National Astronomical Observatories，Chinese Academy of Sciences，Beijing 100012，China；2.University of the Chinese Academy of Sciences，Beijing 100049，China)

Under some circumstances in using the Global Navigation Satellite System(GNSS)，since navigation signals from the satellites are blocked a receiver cannot simultaneously track four or more satellites to estimate its 3-dimensional(3D)coordinates and clock bias.This paper proposes a Doppler Shift-and-Range(DS-R)positioning algorithm with which pseudoranges and Doppler shifts are simultaneously measured.The measurement results are used as inputs to four equations in the algorithm，and the 3D position can be estimated from the equations.Through this approach the algorithm can achieve real-time 3D positioning.By synthesizing multi-frequency observational results and adopting a new method of jointly using code-carrier phases，this algorithm expectably has accuracies similar to those of the standard approach of point positioning.

GNSS；Doppler shift；DS-R algorithm；Real-time positioning

CN53－1189/P ISSN1672－7673

1 Introduction

The trilateration algorithm based on satellite ranging is generally adopted as the positioning method for the Global Navigation Satellite System(GNSS)[1－2].At a location to be positioned，the measured distance to each satellite is used as the radius of a sphere centered at the satellite.The location is at the common intersection of the three spheres，which allows the coordinates of the location to be unambiguously calculated from the well calibrated coordinates of the satellites using the space geometry.In practice，at least one additional satellite needs to be used to take into account the clock bias of the receiver.In situations such as in urban or mountainous areas，electronic shielding can be so severe that simultaneously observable satellites are fewer than four and fall short of the required amount[3].Some aiding techniques must be adopted to achieve 3D positioning with the GNSS in these situations[4－7].A user of the GNSS often does not have a device for the aiding measurement，such as a precise clock or an altitude sensor.This greatly limits the availability of the 3D GNSS positioning based on the trilateration algorithm and aiding techniques.

To avoid the need of aiding equipments researchers have introduced the Doppler-Range(D-R)algorithm which combines Doppler-range measurements of three satellites to compute their 3D coordinates[8].In using the D-R algorithm at least ten minutes of measurement time are generally necessary for accurate positioning，making real-time positioning unachievable with this algorithm[3].

In this paper we propose a new algorithm，the Doppler Shift-and-Range(DS-R)positioning algorithm，which uses simultaneous measurements of pseudoranges and Doppler shifts of two observable satellites.The measured Doppler shift and pseudorange of each satellite can be used to construct a right-circular cone with itsvertex at the position of the satellite.The perimeter of the conical base is specifiable from the pseudorange measurement of the satellite and includes the position of the receiver.The receiver can then be positioned as the intersection of the perimeters of the bases of two cones so determined from the measurements of the two satellites，respectively.The DS-R algorithm can be used for real-time 3D positioning with only two observable satellites.

2 The DS-R Positioning Algorithm

2.1 Pseudorange and Doppler-Shift Measurements

The pseudorange ρ(s)measured through the code phase of a satellite s can be modeled as[9]

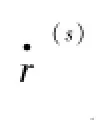
where θ(s)is the angle between the relative velocity v－v(s)and the U(s).

2.2 An Outline of the DS-R Algorithm

As an introduction to the DS-R algorithm，we first consider the simple case of a static receiver so that Eq. (3)becomes

Similarly，if the pseudorange and Doppler shift of another satellite in the view(denoted as satellite m) are measured，we have a new virtual right-circular cone whose vertex is at the satellite m，and have equations for the pseudorange similar to Eq.(7).The receiver is also on the perimeter of the base of this cone.The intersection of the perimeters of the two conical bases uniquely corresponds to the position of the receiver (Figure 1)，which allows the 3D coordinates of the receiver to be geometrically calculated.The performance of the DS-R algorithm will be investigated in Section 3.

Fig.1 Illustration of applying the DS-R positioning algorithm to a stationary receiver

3 Simulations of using the DS-R Algorithm and an Evaluation of the Performance of the Algorithm

3.1 Simulations

Our simulations adopt certain TLE(Two-Line Element)data sets of GPS satellites.The TLE is a data format designated by the North American Air Defense Command and it can be used to describe orbit elements. A TLE data set can be directly input into the SGP4 model(or one of the SGP8，SDP4，and SDP8 models)to compute the position of a satellite at a particular moment.We select twelve cities in the world as locations to be positioned.These cities represent various regions in the five continents.The selection of these cities provides a rather fair evaluation of the performance of the algorithm in potential applications across the world.In the simulations，the UERE(User Equivalent Range Error)，which is generated through code phase measurements，is assumed to be 5m；it is also assumed that Doppler shifts are measured with a precision of 0.01Hz.The positioning results are computed for moments of one-minute intervals over a 24-hour period.Table 1 lists the median positioning errors and 95% confidence level positioning errors according to the simulations.

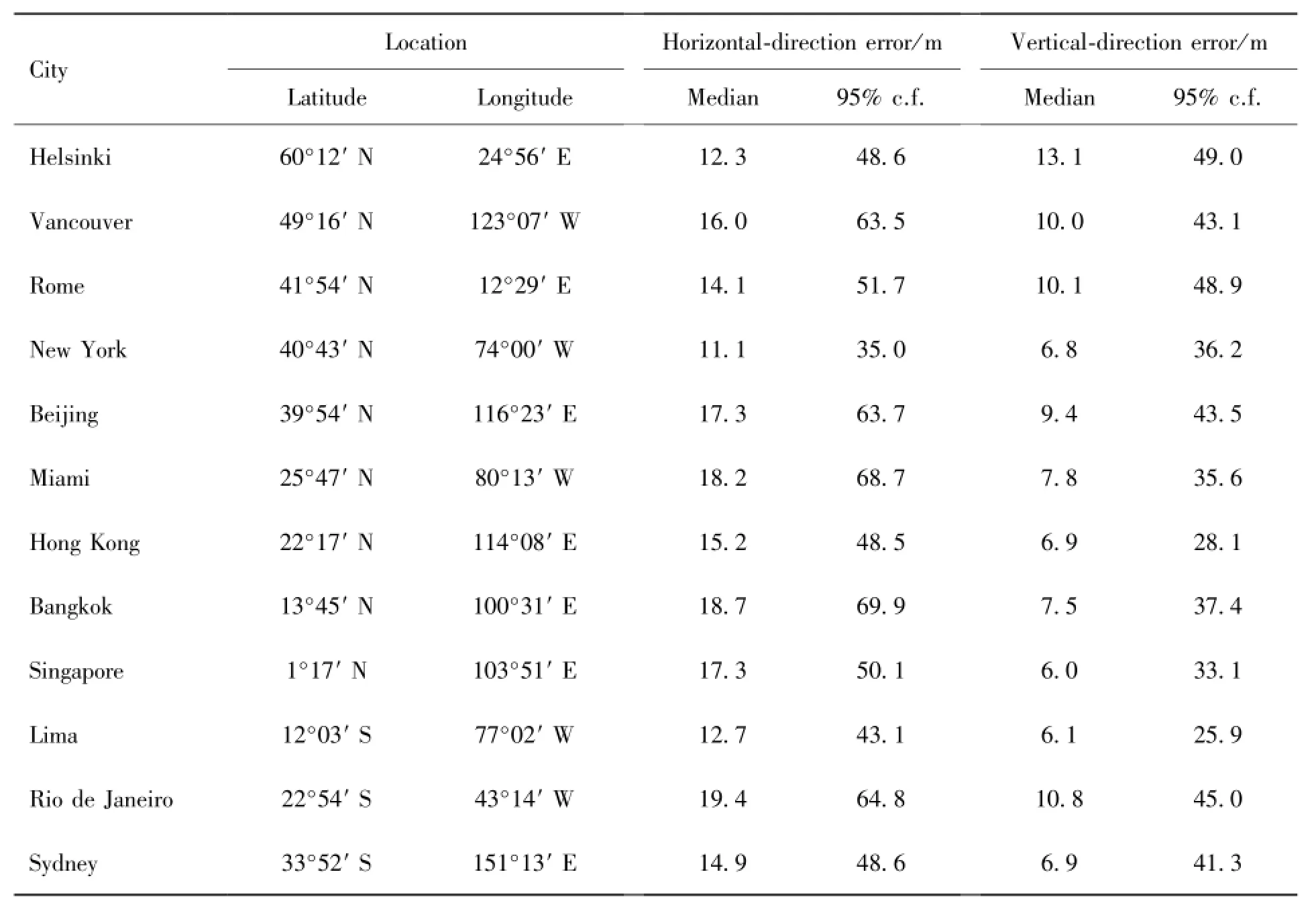
Table 1 The median positioning errors and 95% confidence level(95%c.f.) positioning errors for the twelve cities in the simulations

It can be seen from Table 1 that for most of the twelve cities the 95% confidence level errors are below 65 m and 45 m in the horizontal and vertical directions，respectively.

3.2 An Evaluation of the Performance

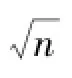
Furthermore，adopting a new approach of jointly using code-carrier phases pseudorange measurements can be accurate to a centimeter level in a sub-second period[14].If the multiple-frequency averaging and the new approach are both adopted，the performance of the DS-R algorithm may match that of the standard approach of point positioning.

As for a mobile receiver with a known velocity，the accuracy of the DS-R algorithm remains the same. However，for mobile receivers with unknown velocities the DS-R algorithm may not be sufficiently effective.A modification of the algorithm needs to be investigated in future.

4 Conclusion

In this paper we propose the DS-R positioning algorithm to achieve effective positioning under some circumstances of using the GNSS not treatable by conventional approaches.The circumstances include those under which there are less than four observable satellites，as to be encountered in some regional navigation systems under development[13－14].The DS-R algorithm can result in real-time 3D positioning by using simultaneous measurements of Doppler shifts and pseudoranges of only two satellites.The requirement of only two observable satellites is the basis for this algorithm to be applicable under some circumstances where conventional methods fail.

[1] Kaplan E D，Hegarty C.Understanding GPS:principle and application[M].Norwood，US: Artech House，2006.

[2] Parkinson B W，Spilker J J.Global positioning system:theory and applications[M].Washington，DC，USA:American Institute of Aeronautics，1996.

[3] Zou B，Zhang N T.Dilution of position in the Doppler-range satellite positioning algorithm[C]// Communication Technology Proceedings.WCC-ICTT，2000:1141－1144.

[4] Mark A S.GPS navigation using three satellites and a precise clock[J].Journal of the Institute of Navigation，1983，30(2):146－156.

[5] Mcburney P，Braisted P.Use of an altitude sensor to augment availability of GPS location fixes [P].US Patent，2000，055，477.

[6] Ptasinski P，Cecelja F，Balachandran W.Altitude aiding for GPS systems using elevation map datasets[J].Journal of Navigation，2002，55(1):451－462.

[7] Ai G X，Sheng P X，Du J L，et al.Barometric altimetry system as virtual constellation applied in CAPS[J].Science in China Series G，2009，52(3):376－383.

[8] Bahrami M，Ziebart M.Instantaneous Doppler-aided RTK positioning with single frequency receivers [C]//Position Location and Navigation Symposium.IEEE/ION，2010:70－78.

[9] Misra P，Enge P.Global positioning system:signal，measurements，and performance[M].Lincoln，US:Ganga-Jamuna Press，2006.

[10] Ma L H，Ai G X，Ji H F.A positioning method integrated with Doppler velocity method in GNSS [P].PRC Patent，201110164385.1.

[11] Ai G X，Shi H L，Wu H T，et al.The principle of the positioning system based on communication satellites[J].Science in China Series G，2009，52(3):472－488.

[12] Ma L H.The benefits of inclined-orbit operations for geostationary orbit communication satellites [J].Artificial Satellites，2011，46(1):1－7.

[13] Ai G X，Ma L H，Shi H L，et al.A method of improving positioning precision in satellite navigation systems[P].PRC Patent，201210090864.8.

[14] Ai G X，Ma L H，Shi H L，et al.Achieving centimeter ranging accuracy with triple-frequency signals in C-band satellite navigation systems[J].Navigation，2011，58(1):59－68.

GNSS中结合多普勒频移的DS-R定位新方法

季海福1，2，马利华1，艾国祥1，王 萌1
(1.中国科学院国家天文台，北京 100012；2.中国科学院大学，北京 100049)

在一些特定的GNSS定位应用中(比如城市或者山区)，因为信号的遮挡，接收机无法同时跟踪到4颗以上的卫星以估算三维位置和钟差。提出一种新的DS-R(Doppler Shift-Range)定位算法:在任意历元，同时观测2颗可视卫星的多普勒频移和码相位，可以等效地获得4个观测方程。DS-R算法利用2颗可视卫星就能实现实时的三维定位。结合多频观测和三频相－码组合新方法，DS-R算法具有与标准单点定位相当的定位性能。DS-R算法为位置估算提供双倍的冗余信息，当可见卫星数较小、传统的定位算法失效时，可作为一个较好的替代定位算法。

全球导航卫星系统(GNSS)；多普勒频移；DS-R算法；实时定位

U666.134

A

1672－7673(2014)01－0013－06

2013－01－15；修定日期:2013－02－04

季海福，男，博士.研究方向:卫星导航与通信.Email:jihaifu＠live.com