超强磁场下的相对论电子

宋冬灵，高志福，王娜，杨文军，彭秋和

(1.信息工程大学理学院，河南 郑州 450001；2.中国科学院新疆天文台，新疆 乌鲁木齐 830011；3.南京大学天文与空间科学学院，南京 210093)

超强磁场下的相对论电子

宋冬灵1，高志福2，王娜2，杨文军2，彭秋和3

(1.信息工程大学理学院，河南 郑州 450001；2.中国科学院新疆天文台，新疆 乌鲁木齐 830011；3.南京大学天文与空间科学学院，南京 210093)

在以前工作的基础上，推导出超强磁场下简并的、相对论的电子压强Pe的普遍表达式；讨论了电子的朗道能级量子化；探索了量子电动力学效应(QED)对中子压强占主导的理想的n-p-e气体系统的影响。主要结论包括:Pe与磁场强度B、物质密度ρ及电子丰度Ye有关；磁场越强，电子压强越大；增加的压强是由高值的电子费米能引起的；在超强磁场下，磁星内部总压强是各向异性的；如果考虑到各向异性的总压强，磁星可能是一种更致密、形变后类似于椭球状的中子星；如果考虑到磁场能对状态方程的正能量的贡献，相对于普通射电脉冲星，磁星的质量可能更大些。

磁星；朗道能级；超强磁场；电子费米能；电子压强

CN53－1189/P ISSN1672－7673

磁星是指一类主要辐射能量来源由磁场能提供的脉冲星，其表面偶极磁场B～1014－1015G，约为普通射电脉冲星的102～103倍(个别磁星除外)。磁星大致被归为两类[1－3]:反常X射线脉冲星(AXPs)和软γ射线重复暴(SGRs)。1996年Thompson与Duncan曾经预言:在磁星内部可能存在更高的强磁场[4]。在中子星内部，中子是超流的，质子是超导的。中子超流可以分为两种态:各向同性的1S0态和各向异性的3P2态。而库柏对的形成是一种普遍存在的量子力学上的超流或超导凝聚现象。磁星的超强磁场可能起源于3P2各向异性的中子超流库柏对的磁矩顺磁所产生的感应磁场[5－6]。产生这样的磁场需要的条件有:适当的低温(T≪Tcr＝2.87×108K，Tcr是3P2中子超流体的临界温度)以及较高的物质密度(ρ～0.5ρ0＜ρ＜2.0ρ0)。根据模型[5－6]，质量大的磁星，其磁场强度也较大，最大的磁场强度约为B～(3.0～4.0)×1015G。

中子星环境中相对论电子的丰度(Ye＝ne/nB，ne是电子数密度；nB是重子数密度)和电子费米能是两个重要的物理参量，它们直接影响了包括MURCA过程、β衰变、电子俘获、中微子和反中微子的吸收等在内的弱相互作用过程；这种影响又会改变原有的物态方程，直接影响了中子星的内部结构及其热演化，甚至会影响到中子星的整体性质。因此，对超强磁场下电子费米能、电子的压强研究具有重要意义。

对于一个完全简并的相对论电子米能的表达式为:

式中，pF(e)为电子的费米动量。在弱磁场极限下，B≪1(B＝B/Bcr，Bcr为电子的临界磁场)，物质压强可写为多种形式:

式中，K及Γ是常数，在下列两种极限情况下:

关于超强磁场对中子星物质组成及物态方程的影响，在以往工作中，很多作者已经进行了详细的研究[7－9]。按照流行的观点:在超强磁场下，电子费米能随磁场强度增强而降低，电子压强也因此而降低。对于这个流行观点，一方面，由于在地球上人们不能得到如此高的强磁场，因此无法在实验室进行验证；另一方面，在计算电子费米能和电子压强时，先是引入一个人为的假设，再运用非相对论电子回旋运动方程的解[7－9]，关于这种严重违背朗道能级量子化的错误方法具体分析，在第3部分进行了介绍。

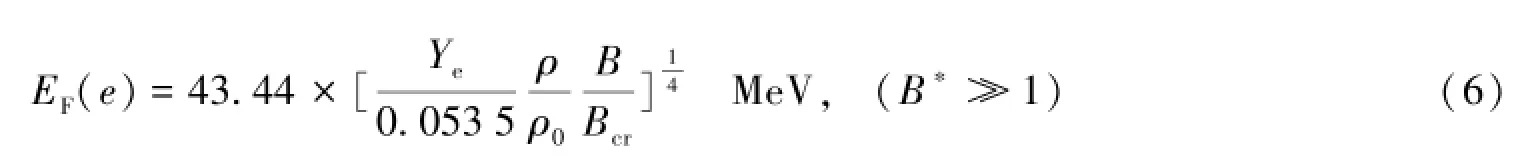
式中ρ0＝2.8×1014g·cm－3是标准饱和核密度。(6)式意义在于，磁场越强，电子费米能就越高，高值的电子费米能可能源于磁场的自由能。

其余部分组织如下:在第1节，继续运用狄拉克δ函数，在以前工作基础上推导出超强磁场下电子压强的表达式；在第2节，讨论了强磁场下的量子电动力学(QED)效应；在第3部分，对强磁场下电子压强随磁场强度变化的两种截然不同的观点进行对比；在第4节对本文做了小结。值得强调的是，本文引入的磁星具有典型的表面偶极磁场Bdip～(1014－1015)G，并且内部磁场不超过B～1017G，在这样的磁星模型下，电子反常磁矩对物质系统总的能态密度ε和总的压强P的贡献很小，可以忽略不计；磁场对电子压强Pe的影响也很小，忽略不计，即采用一个准各向同性的电子压强。

1 超强磁场下的相对论电子的压强

将电子的磁矩假定在一个沿着z轴方向的匀强磁场B上。磁场的矢势采取朗道规范:＝(By，0，0)。对于一个超强磁场(即超相对论的磁场)，通过解相对论狄拉克方程可以获得电子在超强磁场中的能级，

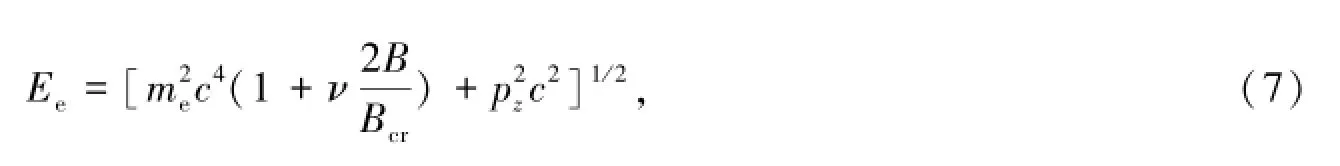
最大的朗道能级数nmax由[pF(z)c]2≥0这一特定条件确定[7]:

式中，Int[x]表示对待定量x取整数。相应地，最大量子数νmax可以表示为:

比较(11)式中两式，很容易得到:

根据以上近似关系，可以求出垂直动量的最大值p⊥(max)，

于是可得:

当n＝0时，电子的朗道能级是非简并的，pz存在最大的值pz(max)，

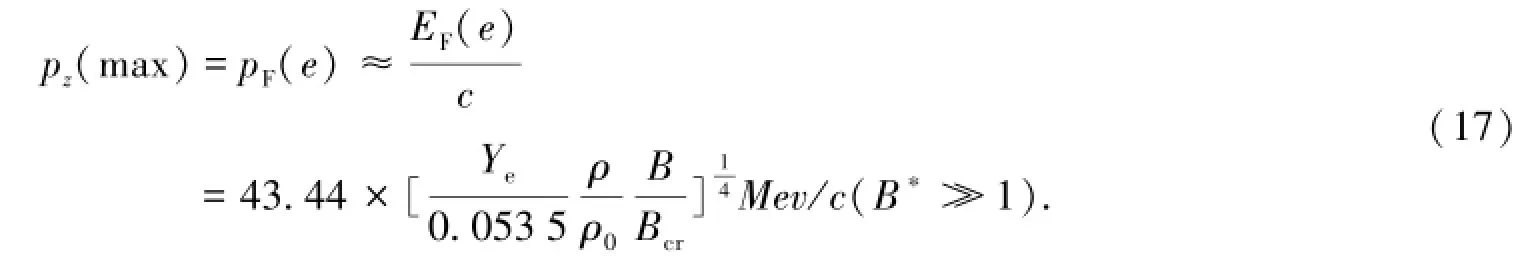
从(16)和(17)式得到:pz(max)＝p⊥(max)＝pF(e)，这也意味着电子压强在平行于磁场方向的分量pz(e)与垂直于磁场方向的分量p⊥(e)近似相等，这是因为在磁星内部电子是简并的、超相对论的，尽管存在着朗道能级，但是电子可以看成是理想的费米气体，因此，电子在各个方向压强近似认为是相等的。超强磁场中的电子压强可由下式给出:

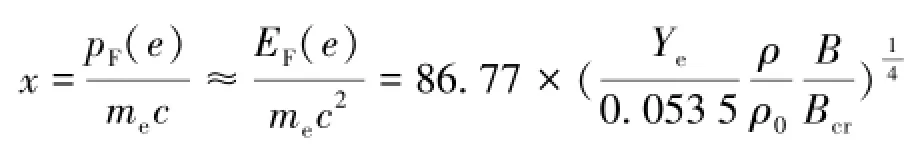
结合(6)式和(20)式，可得到在超强磁场下电子压强与电子费米能的关系式:

很明显地，从(21)式可知，在超强磁场下，电子压强与电子费米能的四次方成正比。由于电子费米能随着磁场的增加而升高，所以，电子压强也必然随磁场的增强而增大。根据(20)式，可作出电子压强随磁场强度变化关系的图像，如图1。

在图1中，选取ρ＝ρ0、Ye＝0.06、B～(1.0×10－3.0×1015)G，对应电子压强Pe～(1.592×1031～4.776 ×1032)dynes·cm－2。图1表明，在给定ρ及Ye的情况下，Pe随着B的增强而增大。

根据(20)式，还作出Pe随ρ变化的图像，如图2。在图2中，选取电子丰度Ye＝0.06，物质密度ρ～(1.0×1014－5.6×1014)g·cm－3，实线、点—冲撞线、冲撞线分别表示B≪1、B＝6.0×1014G及B＝3.0×1015G 3种情况，对应Pe范围分别为:(1.471×1030～1.454×1032)dynes·cm－2、(3.411×1031～1.910×1032)dynes·cm－2、(1.521×1032～8.545×1032)dynes·cm－2。图2的意义在于，在给定B及Ye的情况下，电子压强随着物质密度的增加而增大。正如之前的研究[10－11]指出的那样，较高的电子费米能来自于磁场自由能的释放。既然Pe与(e)成正比，而(e)又随B的增强而增加，因此，Pe也随着B的增强而增加。

图1 在超强磁场下电子压强随磁场强度的变化关系Fig.1 The relation between Peand B

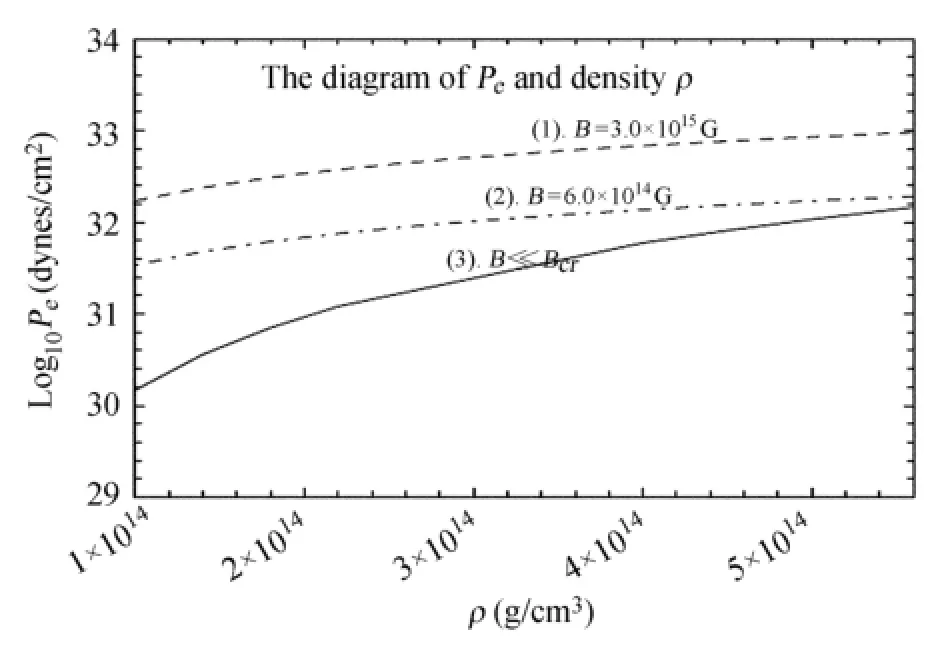
图2 在超强磁场下电子压强随物质密度变化关系Fig.2 The relation between Peand ρ for super-strong B values

2 量子电动力学效应

在超强磁场下由量子电动力学(QED)效应可得到一些有趣的现象，其中一个量子电动力学效应是真空极化。真空极化能够引发朗道能级的极大分离、改变介质的介电性能、激发共振的光子模式转换；由于真空极化降低了粒子回旋加速运动吸收线的等效宽度，使得这个吸收线更加难以观察[13－14]。最近，由XMM、ASCA、RXTE和INTEGRAL高能卫星的观测结果显示:在磁星的光谱中普遍有硬X射线谱成分[14－19]。一些作者运用超强磁场中的相对论电子的共振康普顿散射(RCS)去解释上述观测结果[19－23]。共振康普顿散射也是由于量子电动力学效应引起的一种有趣的现象，并且已经被作为是解释磁星硬X射线辐射机制的主要理论根据。最近，有关量子电动力学效应还普遍存在于磁星的自转减慢和热演化的过程中[24]。

然而，本节关注的是磁星内部中子压强占主导的、理想的n-p-e物质系统中的量子电动力学效应。关于n-p-e理想的气体，其密度范围ρ～(0.5ρ0～2ρ0)，其中电子是简并的、相对论的，中子和质子是简并的、非相对论的。对于超强磁场中n-p-e理想气体的状态方程的处理方法介绍如下:由于在弱相互作用过程中产生的中微子都能逃离星体，因此，假定中微子的化学势为零，即中微子数密度为零，然后根据β平衡条件要求，费米子的化学势满足:

式中，μe是包括了静质能mec2在内的电子化学势，即电子的费米能EF(e)；μp是不包括静质能mpc2在内的质子化学势；μn是不包括静质能mnc2在内的中子化学势。结合(6)式及动量守恒pF(p)＝pF(e)，给出在超强磁场下的质子化学势μp的表达式，

和无量纲的质子费米动量的表达式，

由(22)式可得到无量纲变量:

这样，就得到了在超强磁场下各向同性的物质压强Pm，

(26)式的适用条件:B≫1及ρ～(0.5ρ0～2.0ρ0)。由于总的物质能量密度em与总的物质压强Pm存在着正相关的联系，

式中，nB是重子数密度。对于在强磁场下的理想n-p-e系统，(27)式中Pm包括电子压强Pe、质子压强Pp和中子压强Pn。结合(26)式和(27)式，不难得出下列结论:总的物质能量密度em随着磁场强度B的增强而增加。

中子星内部存在着相对稳定的磁流体动力学平衡，内部结构可用下面的Tolman，Oppenheimer and Volkov(TOV)方程[25]描述:

式中，G是万有引力常数；P(r)是半径为r的球面上总的引力塌缩压；m(r)是半径为r的球内总的物质质量。值得注意的是，TOV方程假定中子星结构是完全球对称形式(即不考虑旋转、不对称的磁压等引起的形变)，并假定磁场的梯度为零(即采用一个统一的磁场)，尽管这些假定与中子星实际情况不符合，然而，这些假定不影响以下讨论的结果:

给定一个中心物质密度ρ，对(28)式进行数值积分可得到质量—半径关系。而这里关注的不是中子星的质量—半径的定量关系，而是超强磁场下磁星质量m(r)随磁场强度B变化关系的定性分析。结合(27)和(28)式，当磁星星体半径r＝R给定时，总的物质能量密度em的最大值与中心物质密度ρ存在正相关；总的质量m(r)也随着中心密度ρ的增加而增大；(28a)式中向内的引力塌缩压P(r)总是与向外的动力学压强相平衡，动力学压强主要来源于费米子简并压(理想的n-p-e系统中子简并压占主导)，不计磁压的影响，动力学压强近似等于总的物质压强Pm；在磁星的核心r→0处，引力塌缩压P(r)及总的物质能量密度em达到最大值，这些最大值又会随着磁场强度B的增强而增加；结合(26)、(27)及(28)式，给定中心密度ρ及磁星星体半径r＝R，磁星总的质量m(r＝R)随着磁场强度B的增强而增加，因此，与普通的射电脉冲星相比较，磁星的质量可能会更大些，较大的磁星质量可能来源于磁星超强磁场自由能的正能量贡献。

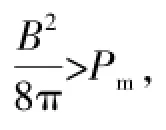
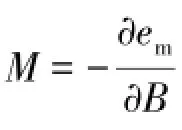
当磁场强度B≪1020G时，磁化强度M与外加磁场B的方向相反，即M＜0，由于这种逆磁效应的存在，有可能发生P⊥＞P‖。当磁场强度B≥1020G时，磁化强度M与外加磁场B的方向相同，即M＞0，由于这种顺磁效应的存在，有可能发生P⊥＜P‖。然而，观测表明，典型的磁星表面偶极磁场Bdip～(1014－1015)G，并且内部磁场不会超过1017G，因此，B2/8π≫MB，在这样的磁星模型下(B≪1020G)，核子的反常磁矩对总的状态方程的影响忽略不计，本文不考虑总压强的磁化项。换句话说，扣除磁化项不会影响本文的以下结论:根据磁星模型，对强磁场下的理想的n-p-e气体，垂直于磁场方向的总压强大于平行于磁场方向的总压强，P⊥＞P‖，这种压强的不平衡性可能导致磁星的结构发生形变，使得磁星具有类似于地球一样的椭球状的几何外形。值得强调的是，由于自转，惯性离心力也会使磁星产生类似于地球形状的形变趋势，然而，这种由于自转效应引起的形变趋势与本文讨论的磁效应引起的形变趋势相比太小，可以忽略不计，详细地对比这两种效应可能会是未来工作的目标之一，本文将不再做较深入的探讨。

在Bocquet et al(1995)的工作中[31]，他们也考虑了电磁张量对高度磁化的中子星结构的影响，然而，他们得到沿着对称轴(z轴)方向总的能量—动量—张量是负值，结果星体沿着对称轴方向塌缩成为薄饼状。与Bocquet et al(1995)的工作恰好相反，我们得到沿着对称轴(z轴)方向总的能量—动量—张量是正值，因为随着磁场的增强，总的物质压强比磁压增加得更快；尽管本文的结果和文[31]存在不同，但是在本文的模型中也会发生类似于文[31]中的磁效应，即在沿磁场方向的磁力作用下，磁星会沿着垂直于赤道方向缩短(不会完全塌缩)或者形变，最终会使得磁星具有类似于地球一样的椭球状的几何外形。相对于磁场较弱的普通射电脉冲星，这种椭球状的磁星可能会更加致密、质量更大些，较大的质量可能源于磁场自由能对系统的状态方程的正能量贡献。

3 关于强磁场下电子压强的两种不同观点

按照流行的观点，在强磁场中，电子压强Pe同电子费米能EF(e)一样，都随着磁场强度B的增强而降低[7－8，32]。在六维相空间体积元dxdydzdpxdpydpz内的微观状态数是dxdydzdpxdpydpz/h3。按照Canuto＼＆Chiu(1968)的计算[33]，在强磁场中单位体积内完全简并的相对论电子微观状态数为:

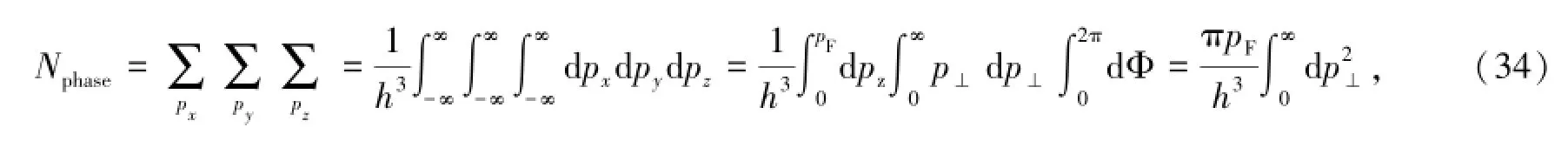
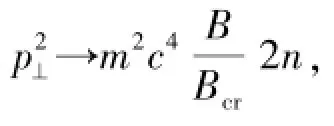
式中引用了非相对论磁场中电子回旋运动方程的解:ћωB＝2μeB。为了讨论方便，取S＝1 cm2及V＝1 cm3，并考虑到电子的自旋简并度gn0＝2－δn0(显然，当n＝0时，g00＝1；当n≥1时，gn0＝2)，由(37)式可得到非相对论磁场中电子朗道能级简并度ωn，

令人困惑的是，如果将(35)式或(36)式与(38)式进行对比，不难发现:相对论磁场中电子的第n个朗道能级上的简并度与非相对论磁场中电子的第n个朗道能级上的简并度完全相同。经过仔细分析发现，(35)和(36)式都不恰当地引用了非相对论磁场中电子回旋运动方程的解ћωB＝2μeB。(35)和(36)两式正好是我们要寻找的表达式，由于不恰当地应用了非相对论磁场中电子回旋运动方程的解而导致了不正确的ωn表达式，最终导致了上述关于电子压强流行性的但却是错误的观点。

下面再列举最具有典型性的两篇论文:Lai.D.，2001(以下简称Paper 1)和Das.U.，and Mukhopadhyay.B.，2012(以下简称Paper 2)中的结论。在Paper 1中的第(6.9)式给出电子压的表达式为:

(引自Lai.D.，2001，参考文献[32])

在Paper 2的第(17)式给出磁场中的电子气压强为:

式中

(引自Das.U.，and Mukhopadhyay.B.，2012，参考文献[38])

Paper 1是一篇综述性文章，作者Lai.D对强磁场中相对论电子物态方程的回顾主要引用自己过去的工作，即本文参考文献[7](Lai＼＆Shapiro 1991)，Paper 2是一篇原创性文章，主要描述磁化白矮星的质量与半径之间的关系，文章对强磁场下的相对论电子的物态方程的回顾完全引用了Lai＼＆Shapiro(1991)的工作，即也是本文中的参考文献[7]，所以Paper 1中的方程(6.10)与Paper 2中的方程(17)两式几乎完全相同(尽管个别物理量表示形式稍微不同)；为了避免重复，参考文献[7]中有关电子态密度和压强表达式就不再列举。

为了精确地描述朗道能级的量子化，必须引入狄拉克δ函数。众所周知，薛定谔方程(或狄拉克方程)的本征波函数能够被扩展成为一个无穷级数，当波函数有界时，通过截断无穷级数，首先给出一个沿磁场方向连续变化的pz，然后解相对论薛定谔方程(或狄拉克方程)，最后可得到电子的最大朗道能级数nmax。逻辑上，首先给定pz，然后决定最大的朗道能级数nmax。这样，方程(35)或(36)应该改写为:

式中，ϕ＝arctan py/px；gn0＝2－δn0(当n＝0时，g00＝1；当n≥1时，gn0＝2)是电子自旋简并度。在计算强磁场下中子星内部电子的微观状态数时，一方面，要根据泡利不相容原理，单位体积内的电子数等于它的微观状态数，另一方面，必须考虑狄拉克δ函数，否则就会得出“电子费米能与电子压强都随着磁场的增强而降低”错误结论。

4 小 结

首先推导出在超强磁场下(B≫Bcr)简并的相对论电子压强的普遍表达式，首次得出“电子压强随磁场的增强而增大，增加的压强可能是由高值的电子费米能引起的”结论；接着，讨论了“量子电动力学效应”对理想的磁n-p-e气体系统的影响。如果考虑到各向异性的总压强，磁星可能是一种更致密、形变后类似于椭球状的中子星；如果考虑到磁场能对状态方程的正能量的贡献，相对于普通射电脉冲星，磁星的质量可能更大些。最后，通过对比与分析，指出了“在强磁场下电子费能和电子压强随磁场增强而降低”这一流行性观点的错误实质。

致谢：感谢与中国科学院新疆天文台脉冲星小组成员的讨论!

[1] Colpi M，Geppert U，Page D.Period dustering of the anomalous X-ray pulsars and magnetic field decay in magnetars[J].The Astrophysical Journal，2000，529(1):L29－L32.

[2] Kouveliotou C，Dieters S，Strohmayer T，et al.An X-Ray pulsar with a super strong magnetic field in the soft gamma-ray repeater SGR1806-20[J].Nature，1998，393:235－237.

[3] Walter H G Lewin，Michiel van der Klis.Compact stellar X-ray sources[M].Cambridge:Cambridge University Press，2004:547－586.

[4] Thompson C，Duncan R C.The soft gamma repeaters as very strongly magnetized neutron stars. II.quiescent neutrino，X-ray，and Alfven wave emission[J].The Astrophysical Journal，1996，473(1):322－342.

[5] Peng Q H，Tong H.The physics of strong magnetic fields in neutron stars[J].Monthly Notices of the Royal Astronomical Society，2007，378(1):159－162.

[6] Peng Q H，Tong H.The physics of strong magnetic fields and activity of magnetars[C]// Proceedings of the 10thSymposium on Nuclei in the Cosmos Mackinac Island，2008.

[7] Lai D，Shapiro S L.Cold equation of state in a strong magnetic field-effects of inverse Beta-Decay [J].The Astrophysical Journal，1991，383(2):745－751.

[8] Harding A K，Lai D.Physics of strongly magnetized neutron stars[J].Reports on Progress in Physics，2006，69:2631－2708.

[9] Das U，Mukhopadhyay B.Strongly magnetized cold electron degenerate gas:mass-radius relation of the magnetized white dwarf[J].Physical Review D，2012，86(4):042001－042016.

[10] Gao Z F，Wang N，Song D L，et al.The effects of intense magnetic fields on landau levels in a neutron Star[J].Astrophysics and Space Science，2011，334(2):281－292.

[11] Gao Z F，Peng Q H，Wang N，et al.Magnetic field decay of magnetars in supernova remnants [J].Astrophysics and Space Science，2012，342(1):55－71.

[12] Gao Z F，Peng Q H，Wang N，et al.The Landau level-superfluid modified factor and the overal soft X/Gamma-ray efficiency coefficient of a magnetar[J].Astrophysics and Space Science，2011，336(2):427－439.

[13] Bulik T，Miller M C.Spectral effects of the vacuum resonance in soft gamma-ray repeaters[J]. Monthly Notices of the Royal Astronomical Society，1997，288(3):596－608.

[14] Kohri K，Yamada S.Polarization tensors in a strong magnetic field[J].Physical Review D，2002，65(4):043006.

[15] Kuiper L，Hermsen W，Mendez M.Discovery of hard nonthermal pulsed X-ray emission from the anomalous X-Ray pulsar 1E 1841-045[J].The Astrophysical Journal，2004，613(3):1173－1178.

[16] Molkov S，Hurley K，Sunyaev R，et al.The broad-band spectrum of the persistent emission from SGR 1806-20[J].Astronomy and Astrophysics，2005，433(2):13－16.

[17] Mereghetti S，Gotz D，von Kienlin A，et al.The first giant flare from SGR 1806-20:observations using the anticoincidence ahield of the spectrometer on INTEGRAL[J].The Astrophysical Journal，2005，624(2):105－108.

[18] den Hartog P R，Kuiper L，Hermsen W.Detailed high-energy characteristics of AXP 1RXS J170849-400910.Probing the magnetosphere using INTEGRAL，RXTE，and XMM-Newton[J]. Astronomy and Astrophysics，2008，489(1):263－279.

[19] Lyutikov M.Did swift measure gamma-ray burst prompt emission radii?[J].Monthly Notices of the Royal Astronomical Society，2006，369(1):5－8.

[20] Baring M G，Harding A K.Resonant compton upscattering in anomalous X-ray pulsars[J]. Astrophysics and Space Science，2007，308(1/4):109－118.

[21] Nobili L，Turolla R，Zane S.X-ray spectra from magnetar candidates-I.Monte Carlo simulations in the nonrelativistic regime[J].Monthly Notices of the Royal Astronomical Society，2008，386 (3):1527－1542.

[22] Baring M G，Wadiasingh Z，Gonthier P L.Cooling rates for relativistic electrons undergoing compton dcattering in strong magnetic fields[J].The Astrophysical Journal，2011，733(1):61.

[23] Gonthier P L，Eiles M T，Wadiasingh Z，et al.Resonant compton upscattering in high field neutron stars[C]//Lewandowski W，Maron O，Kijak J.Electromagnetic Radiation from Pulsars and Magnetars.Proceedings of a Conference held at University of Zielona Góra，Zielona Góra，Poland.San Francisco:Astronomical Society of the Pacific，2012，466:251.

[24] Battesti R，Rizzo C.Magnetic and electric properties of a quantum vacuum[J].Reports on Progress in Physics，2013，76(1):016401.

[25] Shapiro S L，Teukolsky S A.Black holes，white swarfs and neutron stars:the physics of compact objects[M].NewYork:Wiley-Interscience，1983:121－190.

[26] Bonazzola S，Gourgoulhon E，Salgado M，et al.Axisymmetric rotating relativistic bodies:a new numerical approach for‘exact’solutions[J].Astronomy and Astrophysics，1993，278(2): 421－443.

[27] Khalilov V R.Macroscopic effects in cold magnetized nucleons and electrons with anomalous magnetic moments[J].Physical Review D，2002，65(5):043001.

[28] Perez M A，Perez Rojas H，Mosquera Cuesta H J.Magnetic collapse of a neutron gas:can magnetars indeed be formed?[J].European Physical Journal C，2003，29:111－123.

[29] Perez M A，Perez Rojas H，Mosquera Cuesta H J.Anisotropic pressures in very dense magnetized matter[J].International Journal of Modern Physics D，2008，17(11):2107－2123.

[30] Paulucci L，Ferrer E J，de La Incera V，et al.Equation of state for the magnetic-color-flavorlocked phase and its implications for compact star models[J].Physical Review D，2011，83 (4):043009.

[31] Bocquet M，Bonazzola S，Gourgoulhon E，et al.Rotating neutron star models with a magnetic field[J].Astronomy and Astrophysics，1995，301(2):757－775.

[32] Lai D.Matter in strong magnetic fields[J].Reviews of Modern Physics，2001，73(3):629－662.

[33] Canuto V，Chiu H Y.Quantum theory of an electron gas in intense magnetic fields[J].Physical Review，1968，173:1210－1219.

[34] Canuto V，Chiu H Y.Intense magnetic fields in astrophysics[J].Space Science Reviews，1971，12:3－74.

[35] Kubo R.Statistics Mechanics[M].Amsterdam:North-Holland Publishing Comporation，1965: 278－280.

[36] Pathria R K.Statistics mechanics[M].Singapore:Isevier，2003:280－281.

[37] Landau L D，Lifshitz E M.Quantum mechanics[M].New York:Pergamon Press，1965:459－460.

[38] Das U，Mukhopadhyay B.Strongly magnetized cold degenerate electron gas:mass-radius relation of the magnetized white dwarf[J].Physical Review D，2012，86:042001.

Relativistic Electrons in Super-Strong Magnetic Fields

Song Dongling1，Gao Zhifu2，Wang Na2，Yang Wenjun2，Peng Qiuhe3
(1.Institute of Science，University of Information Engineering，Zhengzhou 450001，China；2.Xinjiang Astronomical Observatory，Chinese Academy of Sciences，Urumqi 830011，China，Email:zhifu＿gao＠xao.ac.cn；3.College of Astronomy and Space Science，Nanjing University，Nanjing 210093，China)

Based on our previous work we derive a general formula for the pressure of degenerated relativisticelectron gas，Pe.The formula is suitable for electron gas in super-strong magnetic fields.Subsequently，we discuss the Landau levels of electrons and investigate the Quantum Electrodynamic(QED)effects on the equations of states(EOSs)for an n-p-e ideal-gas system，the pressure of which is dominantly from neutrons. Our main conclusions are as follows.(1)The Peis related to the magnetic induction intensity B，matter density ρ，and electron fraction Ye.(2)The stronger the magnetic field，the higher the electron pressure.(3) A high electron pressure could be caused by a high Fermi energy of electrons in a super-strong magnetic field. (4)A magnetar could be a neutron star deformed by its anisotropic inner pressure to be near an oblate spheroid and to be more compact than a usual radio pulsar.(5)Because of the positive contribution from the magnetic-field energy a magnetar can have a maximum mass larger than that of a usual radio pulsar.

Magnetar；Landau levels；Super-strong magnetic fields；Electron Fermi energy；Electron pressure

P145.6

A

1672－7673(2014)01－0001－12

2013－03－28；修定日期:2013－07－24

宋冬灵，女，讲师.研究方向:天体物理.Email:dongling120011＠sina.com

高志福，男，助理研究员.研究方向:脉冲星.Email:zhifu＿gao＠xao.ac.cn