一维地下水溶质运移模型多参数反演

程 林，韩龙喜，刘晓华，王 琰，陈奇良

(1.河海大学环境学院，江苏南京 210098;2.南通天虹环境科学研究所有限公司，江苏南通 226600)

一维地下水溶质运移模型多参数反演

程 林1，韩龙喜1，刘晓华2，王 琰1，陈奇良1

(1.河海大学环境学院，江苏南京 210098;2.南通天虹环境科学研究所有限公司，江苏南通 226600)

以一维地下水溶质运移模型为基础，利用微分进化算法重点探讨监测频次、测量误差等因素对纵向弥散系数DL、有效孔隙度n以及水流速度u等参数联合反演结果的影响，并构造瞬时源和连续源两种工况的典型案例来验证该方法的可靠性。结果表明:微分进化算法具有收敛速度快、精度高等特点，能够运用于瞬时源和连续源地下水溶质运移模型水力、水质参数的反演问题。

地下水;溶质运移;微分进化算法;多参数反演;瞬时源;连续源

地下水水力、水质参数识别是环境水力学反问题中一类重要的问题。确定地下水水质模型的相关参数，对进一步的水质预报预警起到了至关重要的作用，具有重要的研究价值和应用背景。反问题基本原理是根据地下水水质模型的控制方程、初始条件、边界条件以及环境水力学的测量数据(浓度数据)来识别方程中的部分或全部参数。Wagner［1］首次采用非线性最大似然估计法同时反演模型参数与污染源特征;王锦国等［2］采用实数编码遗传算法优化反演地下水污染物运移参数;韩一龙等［3］利用模拟退火遗传算法，结合二维非均质各向异性承压含水层模型，对导水系数、贮水系数进行反演计算;魏连伟等［4］基于遗传算法这一全局优化技术，以及地下水的有限元模型，应用到北京市应急水源地水文地质参数的反演中;江思珉等［5］根据已有的监测数据(水位和浓度等)，利用和声搜索算法对地下水污染源和未知含水层参数进行同步反演。

总体而言，关于地下水相关参数反问题主要集中于水位、贮水系数、渗透系数等水力参数的反演或者源强与上述参数的联合反演，对于水力、水质参数的联合反演研究较少;且地下水反问题中对参数反演的方法自身研究较多，而关于地下水多参数联合反演的文献未见反演精度的影响因素研究。针对以上问题，本文利用微分进化算法，结合一维地下水溶质运移模型，构造瞬时源和连续源两种工况下的典型案例，探讨监测频次、测量精度等因素对纵向弥散系数DL、有效孔隙度n以及水流速度u等多参数联合反演结果的影响。

1 地下水溶质运移微分进化反演

1.1 微分进化算法概述

微分进化算法是Rainer Storn和Kenneth Price提出的一种更简单和更有效的基于种群进化的多点搜索算法，同样应用了“优胜劣汰，适者生存”的自然进化法则，故应当归属于演化算法。笔者将一维地下水溶质运移模型的参数识别反问题转化为非线性优化问题，即将参数的反演问题转化为求解式(1)待求优化变量S来获取最优参数的过程。

式中:ρ(x，ti)为x处不同时刻溶质质量浓度计算值;ρobs(x，ti)为x处不同时刻溶质质量浓度观测值。

1.2 约束条件

约束条件包括纵向弥散系数DL、有效孔隙度n与水流速度u的上下界约束以及式(2)的约束。

式中:DL为纵向弥散系数，cm2/min;αL为弥散度，cm;u为水流速度，cm/min。

弥散度是1个与实验尺度有关的参数，根据大量的弥散度土柱实验结果［6］，土柱实验测得的弥散度αL取值为［0.01，1］;有效孔隙度n取值范围为(0，1.0);鉴于地下水流速土柱实验的数据缺少一些综述性的资料，笔者采用前人的一些实验成果［7］，并在此基础上以足够大的数据作为水流速度u的一个上界约束，因此，水流速度u的取值范围可为(0，10.0］。根据式(1)的约束关系，纵向弥散系数DL取值范围为(0，10.0］。

1.3 反演步骤

a.产生初始种群。采用随机方法产生初始种群:

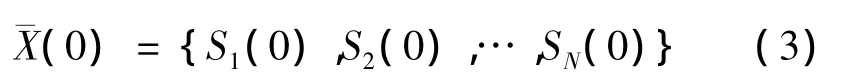
式中:(0)为初始种群，Si(0)为种群中的第i个个体，i=1，2，…，N。

每个个体中有n个待求变量，那么Si(0)可表示为

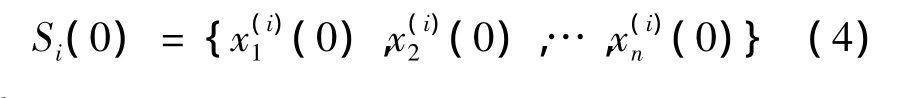
其中，各个变量的初始值用随机方法产生:

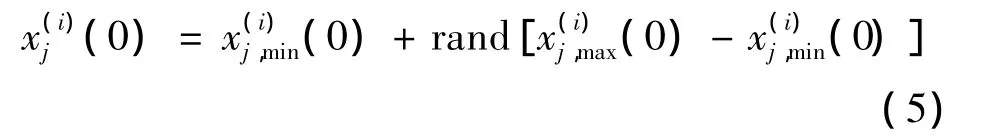
式中:x(i)j(0)为种群¯X(0)中第i个个体Si(0)第j个待求变量的初始值;x(i)j，min(0)，x(i)j，max(0)分别为种群¯X(0)中第i个个体Si(0)第j个待求变量的最小可能值和最大可能值。

b.计算适应值。计算种群中各个个体Si(t)的适应值f(Si(t))，在本问题中，适应值为监测点不同采样时间上的溶质浓度计算值和给定监测值差值的平方和，然后取其平均值:

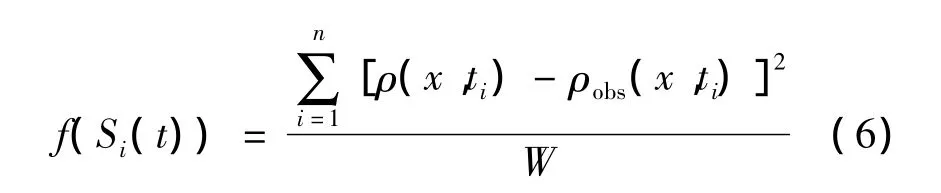
式中:W为监测数据总个数。

c.繁殖。微分进化算法采用特殊寻优原则进行繁殖，对种群中的每个个体Si(t)，通过随机数方法分别生成3个两两不相等的随机整数，r1，r2，r3∈{1，2，…，N}和随机整数jrand∈{1，2，…n}，通过式(8)计算得到1个中间个体:

d.选择进化。当且仅当式(7)中产生的中间个体适应值更好时，该个体才作为进化的个体进入下一代种群中，否则，仍然保留原来的个体，作为下一代生成中间个体的父个体。即，

e.终止检验。当种群代数到达设定的最大代数时，算法结束，将适应值最小的个体作为最优解输出。

2 瞬时源条件下一维地下水溶质运移模型的多参数识别

2.1 瞬时源一维地下水溶质运移模型正问题

不妨假定某含水层中(-∞ ＜x＜+∞)存在一维均匀流场，流动方向为x轴的正向，当对该含水层瞬时投放示踪剂进行试验时，污染源可以概化为瞬时源。当瞬时排放质量为M的污染物质时，排泄区下游污染物浓度变化规律的一维溶质运移模型控制方程为

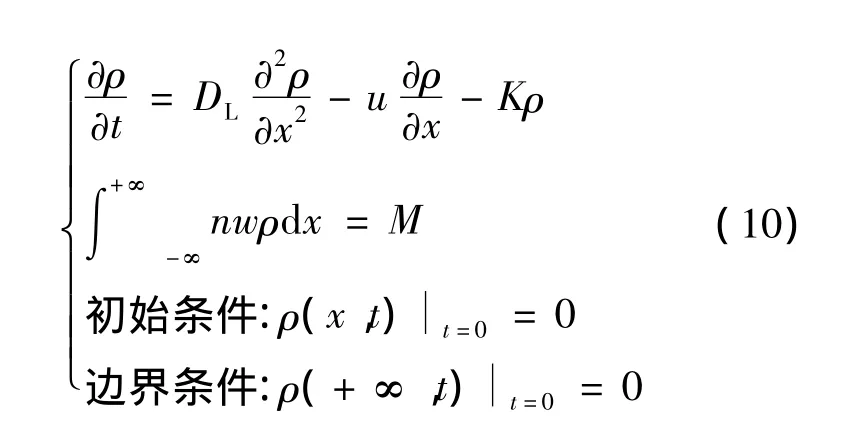
式中:K为降解系数，1/d;w为横截面面积，m2;M为污染物质量，kg。

当溶质为不可降解物质时，即K=0时，该方程通过变化得到如下解析解为

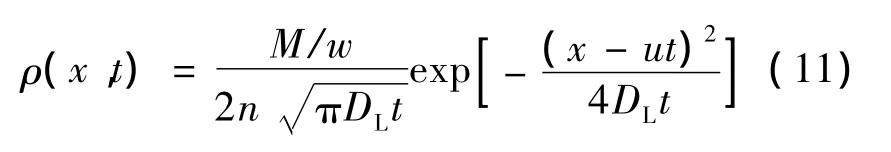
2.2 数值试验

算例1:在某多孔介质柱体中投放10 g示踪剂，柱体横截面面积w为1m2，首先设定准确的水力、水质参数，其中有效孔隙度n为0.3，平均流速u为5.0 m/d，纵向弥散系数DL为0.5 m2/d。为确定参数，利用解析解模型计算得到的一组数据作为一组污染物浓度的监测资料，其数学描述为

以监测点位(x=1.0 m)前提下，分别假定污染物投放0.10 d后，每隔0.05 d监测一次，计算结果见表1。采用本文所提出的微分进化算法自动识别参数DL、n和u，并分析监测频次、测量精度对反演结果的影响。

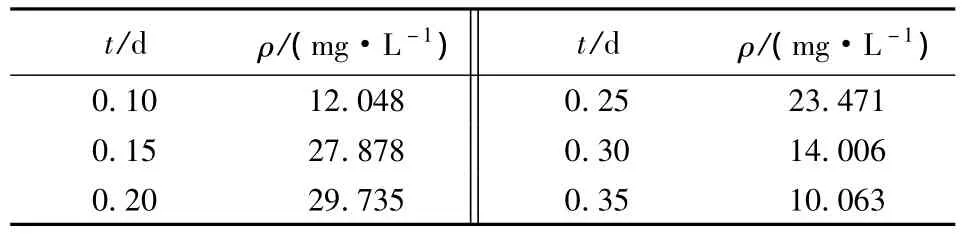
表1 瞬时源示踪剂试验观测数据

2.2.1 监测频次对参数反演结果的影响

为分析监测频次对参数反演精度的独立影响，通过情景分析方法，以监测频次为1次、2次、3次、4次4种工况下进行计算，结果见表2。

表2 不同监测频次瞬时源参数反演结果

2.2.2 测量误差对参数反演结果的影响

不同的监测仪器使得监测的数据精度不同，为研究不同测量误差情况下的微分进化算法的反演精度情况，本次试验观测数据误差采用不同的小数位数来模拟不同仪器下的测量精度，为独立反应情况，4种工况都以监测频次3次为基础，计算结果见表3。

由表2和表3的数值试验可以看出，监测频次和测量误差对瞬时源工况下一维地下水溶质运移模型的纵向弥散系数DL、有效孔隙度n以及水流速度u等多参数的联合反演结果有一定的影响，当监测数据较少，或者测量误差较大时，反演结果出现不稳定的情况，误差较大;但当监测频次大于2，且测量误差多于1位时，反演结果具有较好的稳定性，且能够给出较高精度的反演结果。

表3 不同测量误差瞬时源参数反演结果

3 连续源条件下一维地下水溶质运移模型的多参数识别

3.1 连续源一维地下水溶质运移模型正问题

假定半无限含水层中(0≤x＜+∞)存在一维流场，流动方向为x轴正向，在起始端(x=0 m)连续释放示踪剂，若不考虑混合过程段，则在该断面处质量浓度为ρ0，污染物的迁移扩散规律可以概化为如下公式:

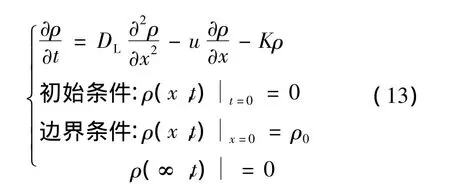
当污染物为不可降解物质时，即K=0时，通过拉普拉斯变换可得这一问题的解析解为

3.2 数值试验

算例2:本算例2的数据引自文献［8］，原为采用erfc(x)近似公式求解地下水弥散系数的算例。在某多孔介质柱体中连续投放浓度为ρ0=3 333.33 g/m3的示踪剂，u=5.0 m/d，DL=0.5 m2/d，在x=1.0m处的不同时刻溶质质量浓度与初始质量浓度的比值见表4。同时采用微分进化算法反演参数DL、u，并分析监测频次、测量精度对反演结果的影响。

表4 不同时刻溶质浓度与初始浓度的比值

3.2.1 监测频次对参数反演结果的影响

为分析监测频次对连续源工况下地下水相关参数反演精度的独立影响，通过情景分析方法，以监测频次分别为1次、2次、3次、4次这4种工况下进行计算，结果见表5。

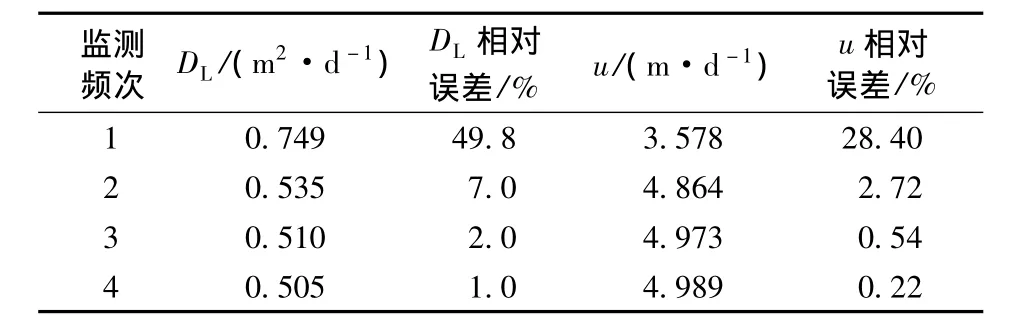
表5 不同监测频次连续源参数反演结果

3.2.2 测量误差对参数反演结果的影响

不同的监测仪器使得监测的数据精度不同，为研究不同测量误差情况下的微分进化算法的反演精度情况，本次试验观测数据误差采用不同的小数位数来模拟不同仪器下的测量精度，为独立反应情况，4种工况下都以监测频次3次为基础，计算结果见表6。

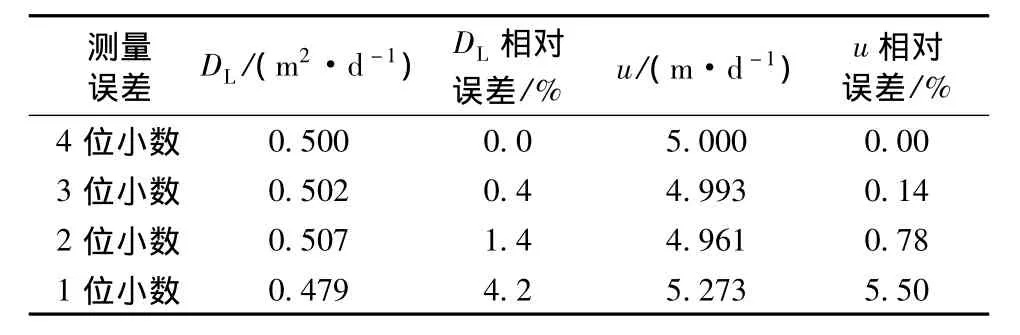
表6 不同测量误差连续源参数反演结果

由表5和表6的数值试验可以看出，监测频次和测量误差对连续源一维地下水溶质运移模型的纵向弥散系数DL和水流速度u等参数联合反演结果有一定的影响，当监测数据较少时，反演结果出现不稳定的情况，误差较大;而测量误差对结果反演影响较小，但当监测频次大于1时，反演结果具有较好的稳定性，且能够给出较高精度的反演结果。

4结语

a.从数值试验结果可知，微分进化算法对瞬时源和连续源两种工况下一维地下水溶质运移模型的水力、水质参数的联合反演能够给出较高的精度。但监测频次和测量误差对参数的反演精度有一定的影响，因此，利用该算法进行反演时，监测数据需要达到一定的要求。

b.在利用微分进化算法的过程中发现，该算法具有收敛速度较快的优点。

［1］ WAGNER B J.Simultaneously parameter estimation and contaminant source characterization for coupled groundwater flow and contaminant transport modeling［J］.Journal of Hydrology，1992，135:275-303.

［2］王锦国，周志芳，黄勇，等.基于实码遗传算法的地下水污染物运移参数反演［J］.水文，2002，22(5):9-11.(WANG Jinguo，ZHOU Zhifang，HUANG Yong，et al.Inverse analysis for parameters of contamination transport in groundwater based on real-coded genetic algorithm［J］.Journal of China Hydrology，2002，22(5):9-11.(in Chinese))

［3］韩一龙，单永明.运用模拟退火遗传算法估计地下水反演参数［J］.计算机工程与应用，2012，48(12):224-228.(HAN Yilong，SHAN Yongming. Using improved simulated annealing genetic algorithm to estimate parameters in groundwater inverse problem［J］.Computer Engineering and Applications，2012，48(12):224-228.(in Chinese))

［4］魏连伟，邵景力，张建力，等.遗传算法在水文地质参数反演中的应用［J］.工程勘察，2004(3):28-31.(WEI Lianwei，SHAO Jingli，ZHANG Jianli，et al.Application of generic algorithm to inversion of hydrogeological parameters［J］.Geotechnical Investigation ＆ Surveying，2004(3):28-31.(in Chinese))

［5］江思珉，蔡奕，王敏，等.基于和声搜索算法的地下水污染源与未知含水层参数的同步反演研究［J］.水利学报，2012，43(12):1470-1477.(JIANG Simin，CAI Yi，WANG Min，et al. Simultaneous identification of groundwater contaminant source and aquifer parameters by harmony search algorithm［J］. Journal of Hydraulic Engineering，2012，43(12):1470-1477.(in Chinese))

［6］马建良，陈喜，程勤波，等.一维变密度溶质运移实验及参数推求［J］.水资源保护，2008，24(3):8-11.(MA Jianliang，CHEN Xi，CHENG Qinbo，et al.Identification of hydrodynamic parameters based on one dimensional variable density and solute transport numerical model［J］.Water Resources Protection，2008，24(3):8-11.(in Chinese))

［7］肖先煊，许模，蔡国军，等.基于潜水渗流模型的地下水实际流速［J］.实验室研究与探索，2013，32(4):11-14.(XIAO Xianxuan，XU Mo，CAI Guojun，et al.On actual flow velocity of groundwater based on diving percolation model tests［J］.Research and Exploration in Laboratory，2013，32(4):11-14.(in Chinese))

［8］王军辉，周志芳.erfc(x)近似公式及其在求解地下水运移参数中的应用［J］.河海大学学报:自然科学版，2001，29(3):111-114.(WANG Junhui，ZHOU Zhifang.Approximation of erfc(x)and its application in determining the groundwater transport parameters［J］.Journal of Hohai University:Natural Sciences，2001，29(3):111-114.(in Chinese))

Multi-parameter inversion of one-dimensional groundwater solute transport model

CHENG Lin1，HAN Longxi1，LIU Xiaohua2，WANG Yan1，CHEN Qiliang1
(1.College of Environment，Hohai University，Nanjing 210098，China;2.Nantong Tianhong Environmental Science Research Institute Co.，Ltd.，Nantong 226600，China)

Based on a one-dimensional groundwater solute transport model，the influences of monitoring frequency and measurement precision on joint inversion results of the longitudinal dispersion coefficientDL，the effective porosityn，and the flow velocityuwere studied using the differential evolution algorithm.Two typical cases，the instantaneous source and continuous source conditions，were constructed to verify the reliability of the differential evolution algorithm.Numerical experimental results show that the differential evolution algorithm has the characteristics of fast convergence and high precision，and it can be applied to the inversion of hydraulic and water quality parameters of solute transport models under the conditions of an instantaneous source and a continuous source.

groundwater;solute transport;differentialevolution algorithm;multi-parameterinversion;instantaneous source;continuous source

P641.2

A

1004-6933(2014)03-0005-04

10.3969/j.issn.1004-6933.2014.03.002

程林(1987—)，男，硕士研究生，研究方向为环境水力学。E-mail:chenglin0891@163.com

韩龙喜，教授。E-mail:hanlongxi@sina.com

(收稿日期:2013-07-31 编辑:高渭文)