基于盲数理论的河流健康评价

王兴顺，刘 凌，闫 峰

(河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098)

基于盲数理论的河流健康评价

王兴顺，刘 凌，闫 峰

(河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098)

在介绍盲数理论的基础上，对河流健康评价中所选取的指标值进行盲数化处理，进而利用盲数运算法则和判别模式对各指标进行评价等级判定，得到各指标隶属于各评价等级的可能性。将该方法与传统的综合指数法相结合，构建基于盲数理论的河流健康评价模型，并将其应用于通榆河健康评价，从物理特征、环境特征、生态功能、服务功能等方面构建评价指标体系，识别河流健康状况。结果表明，通榆河的健康等级为“中”，主要问题为水质较差和生物多样性偏低。

盲数理论;不确定性;可信度;综合指数;河流健康评价

作为全球水循环中的重要一环，河流系统是地球上的大动脉，在维系地球水循环、能量平衡、气候变化和生态发展中具有极其重要的作用［1］。近几十年来，河流出现了断流、水质恶化、生物多样性降低等一系列水生态和水环境问题，因此，对于河流健康程度的评价成了研究热点之一。

河流是一个具有庞杂信息的系统，可以用以表达河流健康状况的各项指标，诸如理化指标、生物指标等，都具有一定的不确定性，同时，河流健康这一概念本身也具有一定的模糊性，可见河流健康评价是一项综合处理多种不确定性信息的工作。盲数理论是刘开第等［2］为处理不确定性信息而提出，随后在工程可靠度分析、电网规划和水环境评价等领域得到了比较广泛的应用［3-5］。实践表明，盲数理论可以更加全面、客观地描述这些不确定性问题。因此，如果将盲数概念应用到河流健康评价中，可能会更加有效利用其中的不确定性信息，对河流的健康状况给出更加客观、全面的评价。本文将盲数引入河流健康评价综合指数的计算中，并应用此方法对江苏省境内的通榆河进行健康评价，以期为河流健康评价提供一种新的思路。

1 基于盲数理论的河流健康评价模型

信息的不确定性包括客观上的随机性、模糊性以及主观上的未确知性，将兼具这几种不确定性的信息称为盲信息，以盲信息为描述对象便出现了盲数［2-6］。

1.1 盲数

1.1.1 盲数的定义

g(I)为区间型灰数集，设ai∈g(I)，αi∈［0，1］(i=1，2，…，l)，f(x)为定义在g(I)上的灰函数，且

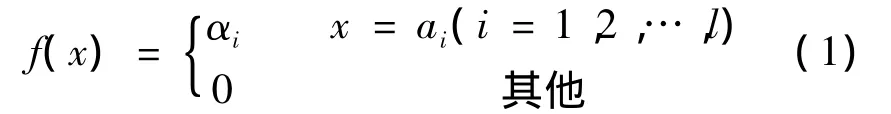
若当i≠j(j=1，2，…，l)时α≤1，则称函数f(x)为一个盲数。称αi为f(x)的ai值的可信度，称α为f(x)的总可信度，称l为f(x)的阶数［7］。

1.1.2 盲数的运算法则

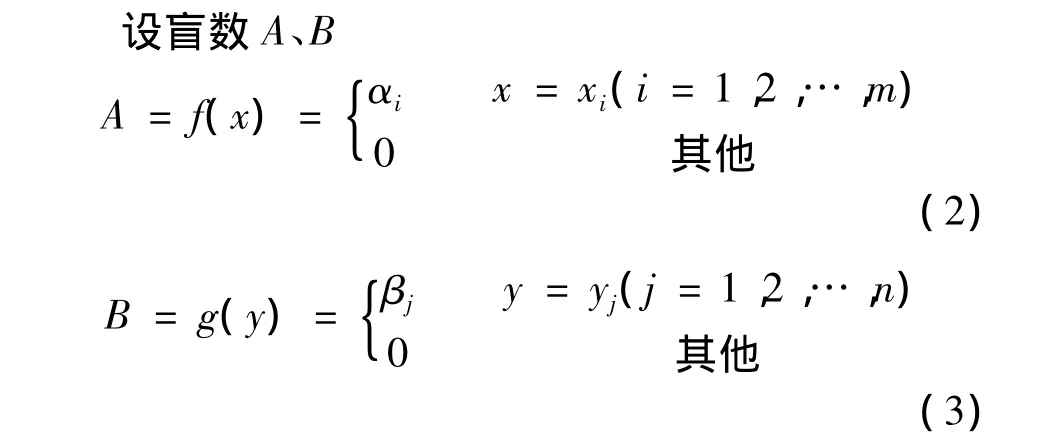
设*表示g(I)中的一种运算，比如是“+、-、×、÷”中的一种，定义:A关于B在*运算下的可能值*矩阵和A关于B的可信度积矩阵分别为

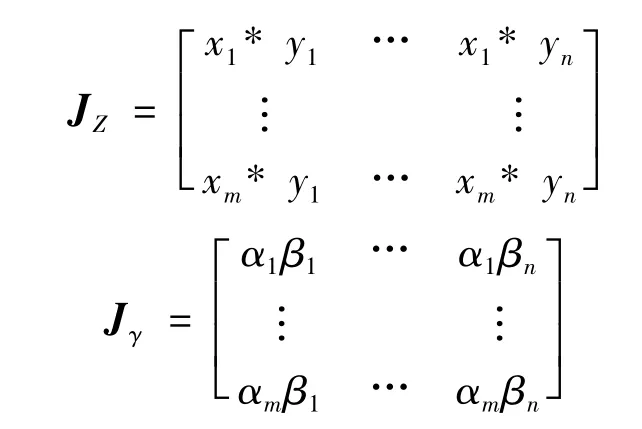
式中:x1，x2，…，xm和y1，y2，…，yn分别为盲数A和B的可能值序列;α1，α2，…，αm和 β1，β2，…，βn分别为盲数A和B的可信度序列。

将矩阵JZ中所有可能值合并相同项后形成一个新的可能值序列z1，z2，…，zk，而矩阵 Jγ中的对应项(如果是合并项，则取Jγ中对应项的和)形成一个新的可信度序列 γ1，γ2，…，γk，则有盲数:

1.1.3 盲数的BM模型

对于式(2)和式(3)定义的盲数A、B，称盲数A关于B的BM模型为

式中:r为某个实际问题给出的已知实数;P为可信度。

1.2 引入盲数的河流健康评价综合指数

1.2.1河流健康评价综合指数

河流健康包含了物理、化学、生物完整性意义上的自然结构和功能状态，以及社会、经济、文化等社会服务功能实现的程度［8-10］，其评价是一种多指标、主客观结合且具有时空差异性的综合评价，所以选取计算综合评价指数的公式［11］为

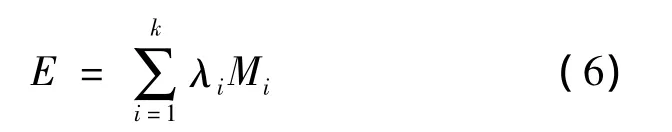
式中:E为综合评价指数;λi为第i个评价指标的权重;Mi为第i个评价指标的等级得分;k为评价指标的个数。

1.2.2 基于盲数的评价等级判定

在式(5)的盲数BM模型中，如果A表示河流健康评价指标值，B表示该指标的评价等级阈值，比如属于优、良、中、差 4 级的等级阈值Y1、Y2、Y3、Y4，假设总的可信度为1，则该指标属于各等级的可信度可用如下公式进行计算［12］:对于越大越优型指标

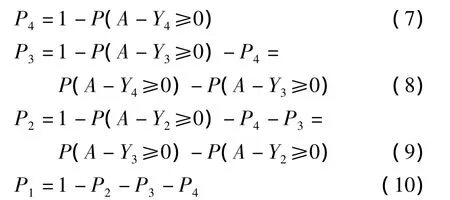
对于越小越优型指标

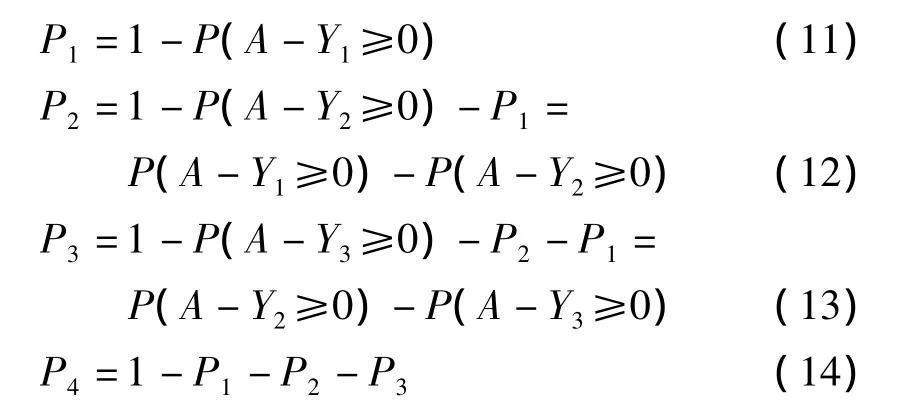
1.2.3 评价指标等级得分和综合指数等级评判

根据加权平均原则［13］，本文选用以中值做权、边值做界的方法进行综合指数等级判定。首先赋予优、良、中、差等距得分 4、3、2、1，求得得分区间中心值y1=3.5、y2=2.5、y3=1.5、y4=0.5，以式(7)～(10)或式(11)～(14)得到的指标值隶属于各等级的可信度序列为权，分别计算各指标的等级得分Mi，即

将式(15)得到的各指标等级得分Mi代入式(6)中，得到河流健康评价综合指数值，最后根据值大小进行综合指数的等级判定，即值所在区间［3，4］、［2，3］、［1，2］、［0，1］分别对应了综合指数的优、良、中、差4个等级。

2 实例分析

通榆河是江苏省江水东引北调工程的骨干输水通道之一，南起南通市新通扬运河，北至连云港市柘汪工业园，全长368 km。通榆河与京杭运河一起构成了江苏省南北向水利、水运的骨干河道，肩负着向江苏省东部沿海地区供水、灌溉、排涝、航运和生态等综合功能，对振兴苏北和保障沿海开发、促进沿线经济社会发展具有重要的意义［14］。针对通榆河的这些主要功能和自身特点，从物理特征、环境特征、生态功能和服务功能4个方面出发，构建通榆河健康评价指标体系。

2.1 评价指标的选取

a.物理特征。河流的物理特征，诸如河流走向、连通性、落差、岸坡稳定性、流量等，会影响河流各项功能的发挥，其与河流原始自然状态的差异更能很好地反映人类活动对于河流系统扰动的程度，所以，物理特征对于河流健康的表征是必不可少的指标。本文选择了河岸稳定性、流动性和生态流量满足程度3项代表性指标评价河流的物理特征。

b.环境特征。对于河流，环境特征最直接的表征就是水质状况，通榆河的主要污染物来源于工农业废水和生活污水，主要污染物为营养盐类，所以选择DO、CODMn和NH3-N作为其水质情况的评价指标。

c.生态功能。从生态的角度进行河流健康评价，即对河流生态系统的结构和功能进行评价，对其完整性和多样性进行判定，这里选择岸坡植被结构完整性、生物多样性作为生态功能评价指标。

d.服务功能。服务功能主要是指河流之于人类各项需求的满足，比如防洪、发电、供水、航运、灌溉、养殖、景观娱乐等。针对通榆河调水、饮用水水源地、排涝和航运等主要功能，选择防洪工程达标率、岸线利用管理、公众满意度、供水保证率等指标作为服务功能的表征。

2.2 评价标准和指标权重

评价指标权重是影响河流健康评价结果的重要因素，本文根据层次分析法［15］，计算各指标的权重，计算结果及各指标评价标准见表1。

2.3 评价计算和结果

根据江苏省水利厅所提供的相关资料和野外实地踏勘所取得信息，利用SPSS软件对这些信息数据进行Q型层次聚类分析，将其划分为若干区段，以各区段内数据占总数据百分比作为对应区段的可信度［12］，构造出如下盲数表示的指标值:

表1 通榆河健康评价指标体系

式中，A1～A12分别为河岸稳定性、流动性、生态流量满足程度、DO、CODMn、NH3-N、岸坡植被结构完整性、生物多样性、防洪工程达标率、岸线利用管理、公众满意度、供水保证率的盲数。

以表1中评价标准的区间上限为相应的等级阈值Y1、Y2、Y3、Y4，根据式(7)～(10)计算各评价指标隶属于各等级的可信度P4、P3、P2、P1，而对于CODMn和NH3-N两项越小越优型的指标，则根据式(11)～(14)计算各评价指标隶属于各等级的可信度P1、P2、P3、P4，然后根据式(15)计算各指标等级得分，最后代入式(6)求得通榆河健康评价综合指数，结果见表2。

由表2可知，通榆河健康评价综合指数计算结果为1.867，属于区间［1，2］，健康等级为“中”，其中，NH3-N和 CODMn等级得分分别为 1.200和1.500，都属于区间［1，2］，等级为“中”，说明水质较差，改善水质是该河流系统急需解决的问题;另外，生物多样性的等级得分为1.500，属于区间［1，2］，等级为“中”，可能是由于人类对于该河流的干扰程度比较大，造成生态功能的减弱。

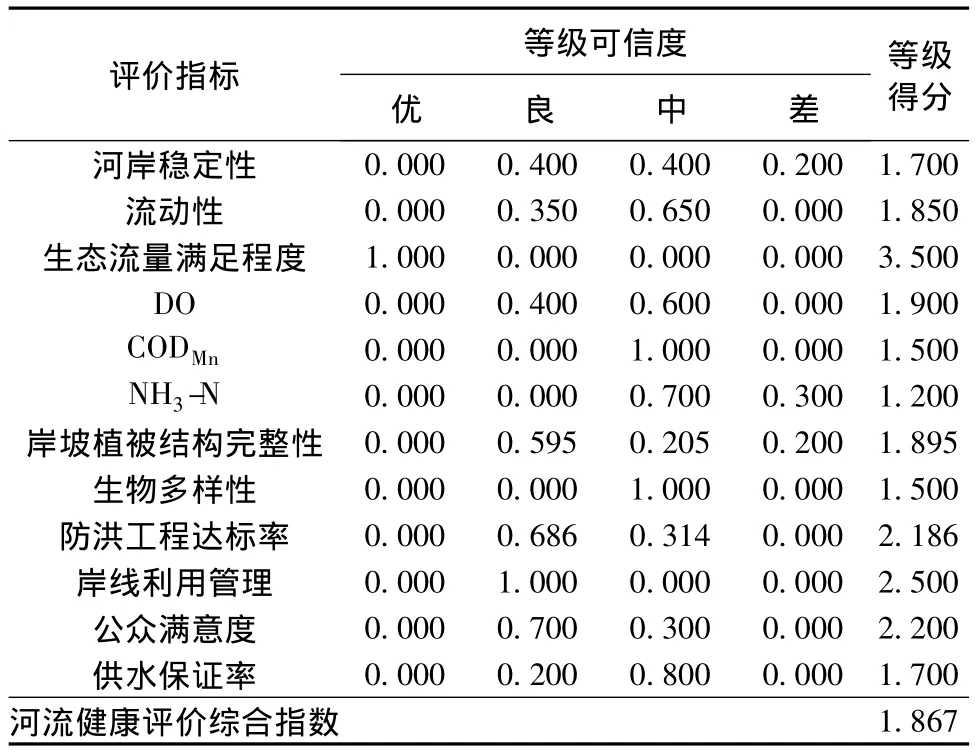
表2 通榆河健康评价综合指数计算结果

3 结论

a.盲数对于类似河流健康评价的不确定性信息具有很强的处理能力，可以较好地保存原始数据所包含的信息，在一定程度上减小了简化计算造成的指标信息损失，可以更加全面地表达评价对象的整体状况。利用盲数化的评价指标值和盲数BM模型进行等级判定，进而结合综合指数法对河流进行健康评价的方法是可行的。

b.在对通榆河的实例分析中，综合评价结果为“中”，河流系统的薄弱环节为水质较差和生物多样性较低，该评价方法比较全面地描述了通榆河的整体健康状况。

［1］夏自强，郭文献.河流健康研究进展与前瞻［J］.长江流域资源与环境，2008，17(2):252-256.(XIA Ziqiang，GUO Wenxian.Research advance in river health［J］.Resources and Environment in the Yantze Basin，2008，17(2):252-256.(in Chinese))

［2］刘开第，吴和琴，庞彦军，等.盲数的概念、运算与性质［J］.运筹与管理，1998，7(3):14-17.(LIU Kaidi，WU Heqin，PANG Yanjun，et al.The concept，operations and properties of blind number［J］.Operations Research and Management Science，1998，7(3):14-17.(in Chinese))

［3］丁丽，顾冲时，孙杰，等.未确知数学在堤防工程安全评价中的应用［J］.水电能源科学，2005，23(4):29-32.(DING Li，GU Chongshi，SUN Jie，et al.Application of unascertained mathematics in levee safety assessment［J］.Water Resources and Power，2005，23(4):29-32.(in Chinese))

［4］高赐威，程浩忠，王旭.盲信息的模糊评价模型在电网规划中的应用［J］.中国电机工程学报，2004，24(9):24-29.(GAO Ciwei，CHENG Haozhong，WANG Xu.The application of fuzzy evaluation of blind information in electric network planning［J］.Proceedings of the CSEE，2004，24(9):24-29.(in Chinese))

［5］李如忠，汪家权，王超，等.不确定性信息下的河流纳污能力计算初探［J］.水科学进展，2003，14(4):459-463.(LI Ruzhong，WANG Jiaquan，WANG Chao，et al.Calculation of river water environmental capacity under unascertained information［J］.Advances in Water Science，2003，14(4):459-463.(in Chinese))

［6］王光远.未确知信息及其数学处理［J］.哈尔滨建筑工程学院学报，1990，23(4):1-9.(WANG Guangyuan.Unascertained information and its mathematical treatment［J］.J Harbin Archit＆ Civ Eng Inst，1990，23(4):1-9.(in Chinese))

［7］刘开第.不确定性信息数学处理及应用［M］.北京:科学出版社，1999.

［8］KARR J R.Defining and measuring river health［J］.Freshwater Biology，1999，41(2):221-234.

［9］董哲仁.河流健康的内涵［J］.中国水利，2005(4):15-18.(DONG Zheren.River health connotation［J］.China Water Resources，2005(4):15-18.(in Chinese))

［10］刘昌明，刘晓燕.河流健康理论初探［J］.地理学报，2008，63(7):683-692.(LIU Changming，LIU Xiaoyan.Healthy river:essence and indicators［J］.Acta Geographica Sinica，2008，63(7):683-692.(in Chinese))

［11］耿雷华，刘恒，钟华平，等.健康河流的评价指标和评价标准［J］.水利学报，2006，37(3):253-258.(GENG Leihua，LIU Heng，ZHONG Huaping，et al.Indicators and criteria for evaluation of healthy rivers［J］.Journal of Hydraulic Engineering，2006，37(3):253-258.(in Chinese))

［12］唐晓娇，黄瑾辉，李飞，等.基于盲数理论的水体沉积物重金属污染评价模型［J］.环境科学学报，2012，32(5):1104-1112.(TANG Xiaojiao，HUANG Jinhui，LI Fei，et al.Assessment model for heavy metal pollution in sediment based on the blind theory［J］.Acta Scientiae Circumstantiae，2012，32(5):1104-1112.(in Chinese))

［13］闫峰，刘凌，徐丽娜，等.隶属度向量分析法在河流健康评价中的应用［J］.水电能源科学，2012，30(10):30-32.(YAN Feng，LIU Ling，XU Lina，et al.Application of membership vector analysis in river health assessment［J］.Water Resources and Power，2012，30(10):30-32.(in Chinese))

［14］黄兴国.河流健康评价理论研究及其应用［D］.南京:河海大学，2012.

［15］赵焕臣.层次分析法:一种简易的新决策方法［M］.北京:科学出版社，1986.

River health assessment based on blind number theory

WANG Xingshun，LIU Ling，YAN Feng
(State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing 210098，China)

Based on the blind number theory，the values of selected indicators in river health assessment were transformed into blind numbers in order to assess the ranks of the indicators with the blind number algorithm and judging mode.As a result，the possibilities of the indicators belonging to each rank were obtained.A river health assessment model was constructed based on the blind number theory with the combination of the proposed method and traditional comprehensive index method and was applied to the Tongyu River’s health assessment.The assessment index system was established from the aspects of physical features，environmental features，ecological functions，and service functions，in order to assess the river’s health.The assessment results show that the health of the Tongyu River was at a medium level and poor water quality and low biodiversity were the main problems of the river.

blind number theory;uncertainty;credibility;comprehensive index;river health assessment

X824

A

1004-6933(2014)03-0014-05

10.3969/j.issn.1004-6933.2014.03.004

国家自然科学基金(51279060);江苏省水利科技项目(2012023)

王兴顺(1985—)，男，硕士研究生，研究方向为水环境演变规律与保护。E-mail:wangxingshun2012@163.com

刘凌，教授。E-mail:lingliu@hhu.edu.cn

(收稿日期:2013-11-26 编辑:徐 娟)