SCE-UA算法在水环境系统优化问题中的应用

张 景，张文婷，邢宝龙

(河海大学水文水资源学院，江苏南京 210098)

SCE-UA算法在水环境系统优化问题中的应用

张 景，张文婷，邢宝龙

(河海大学水文水资源学院，江苏南京 210098)

把SCE-UA算法应用到水环境系统优化问题的求解中，通过对问题的预处理，求解3个典型的优化问题:①二维稳态水质模型横向扩散系数及流速推求;②排放口最优化处理;③水工建筑物优化调度。结果表明:SCE-UA算法不但能求解一元函数约束的优化问题，通过构造罚函数，还能够成功求解有多元函数约束的优化问题。认为该算法不依赖导数和优化问题的具体形式，所需参数极少，求解精度高，通用性较强，值得在环境系统优化中推广。

SCE-UA算法;水环境系统优化;纵向扩散系数推求;排放口优化;水闸调度

在水环境管理的过程中会遇到大量的水环境系统优化问题，如排污口优化设计、水质模型参数识别以及水质优化调度等，这些问题都可以归结为非线性优化问题。目前常用的求解方法有矩法、直线图解法、经验公式法、模糊非线性规划法、智能优化算法等，这些方法有的与水质模型的具体形式有关，且参数的估计精度较难控制［1-2］;有的较为复杂，如遗传算法，其程序的编制异常烦琐且参数众多，使得其应用受到限制。SCE-UA算法参数少，过程简单，在解决水环境系统优化问题中潜力很大。

SCE-UA算法是一种全局优化算法［3-4］。宋星原等［5］把SCE-UA算法、遗传算法和改进的单纯形法应用到三水源新安江模型参数自动优选中，对各种优化算法的应用效果进行分析比较。结果表明，SCE-UA算法综合了遗传算法和单纯形法优点，能够一致、快速地收敛到全局最优解，取得了较为满意的结果。雷晓辉等［6］在分布式水文模型EasyDHM中运用SCE-UA算法进行参数优化，结果表明SCEUA算法是一种能解决高维参数全局优化问题的有效算法。辛朋磊等［7］运用SCE-UA算法进行模型寻优计算，得到合理的水资源优化配置。唐运忆等［8］运用SCE-UA算法对集总式新安江模型汇流参数及半分布式TOPMODEL模型进行参数优化，发现对TOPMODEL参数自动优选的结果好于新安江模型。马海波等［9］用SCE-UA算法对TOPMODEL参数进行优化，并对优化结果进行检验，结果表明SCE-UA算法可用于 TOPMODEL模型参数率定。唐和生等［10］证明SCE-UA算法应用于结构系统识别问题的可行性、稳定性和有效性。

以上研究多是把SCE-UA算法用于水文模型参数的优化，优化问题中含有的约束多是参数的上下限。在水环境系统中，约束多目标优化问题非常常见，但很少采用SCE-UA算法用于模型优化，为此笔者尝试运用该算法求解水环境系统优化问题。

1 SCE-UA算法

1.1 算法的基本步骤

SCE-UA算法的基本思想是把确定性的复合形搜索技术和自然界中的生物竞争进化原理相结合。算法基本步骤如下［3］:

步骤1 问题预处理。利用权重法与罚函数法处理算法中的多目标与约束，使问题成为仅含有自变量界限约束的单目标优化问题。

步骤2 初始化。假定待优化问题为n维问题，选取参与进化的复合形个数p(p≥1)和每个复合形所包含的顶点数m(m≥n+1)，则计算样本点数目s=p·m。

步骤3 产生样本点。在可行域内随机产生s个样本点x1，x2，…，xs，分别计算每一点xi的函数值fi=f(xi)，i=1，2，…，s。

步骤4 样本点排序。把s个样本点(xi，fi)按函数值升序排列，排序后仍记为((xi，fi)，i=1，2，…，s)，其中f1≤f2≤…≤fs，记D={(xi，fi)，i=1，2，…，s}。

步骤5 划分复合形群体。将D划分为p个复合形A1，A2，…，Ap，每个复合形含有m个顶点，其中Ak表示第k个复合形，k=1，2，…，p。

步骤6 复合形进化。按复合形进化算法分别进化各个复合形。

步骤7 复合形混合。把进化后的每个复合形的所有顶点组合成新的点集，再次按函数值fi升序排列，排列后不妨仍记为D，对D按目标函数升序进行排列。

步骤8 收敛性判断。如果满足收敛条件则停止，否则返回步骤5。

1.2 算法的终止准则

①目标函数被调用计算目标值的次数达到最大值Nmax;②目标函数连续循环规定的次数Lmax后仍无法提高规定的精度。

2 优化模型的预处理及求解

SCE-UA算法在以往的应用中常用来求解仅带有决策变量取值范围的约束优化问题，但在水环境系统规划管理过程中，常会遇到无约束优化问题、约束优化问题以及不可导优化问题。针对上述3种情况，分别选取了3个典型实例，并针对不同情况通过不同处理方法，使得SCE-UA算法能够适用不同类型问题的优化求解。实例中各参数取值如表1所示。

表1 各实例参数设置

2.1 二维稳态水质模型横向扩散系数及流速的推求

在断面形状、河底坡降沿程基本不变的河流上游断面的中点，连续稳定排放示踪剂溶液。水流方向为x轴方向，河流横向为y轴方向，坐标原点设在排放点，假设示踪剂溶液在水深方向瞬间混合均匀并忽略河流的纵向扩散作用。在以上条件下求得二维稳态水质模型的解析解为

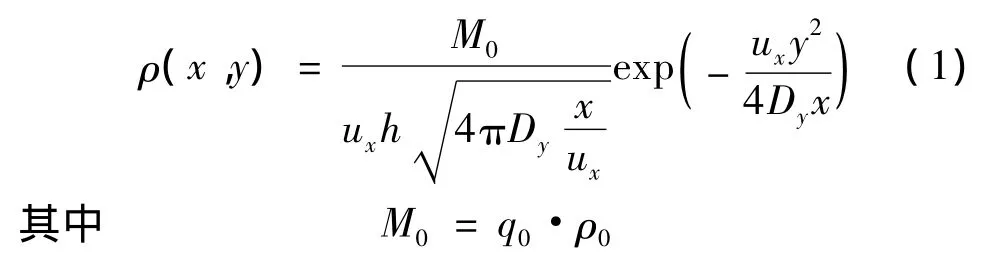
式中:ρ(x，y)为点(x，y)处污染物质量浓度，mg/L;x，y分别为纵、横坐标，m;M0为单位时间内排放的污染物量，即源强，mg/s;ux为河流x向平均速率，m/s;h为河道平均水深，m;Dy为河流y向扩散系数，m2/s;q0为示踪剂流量，L/s;ρ0为示踪剂质量浓度，mg/L。

文献［1］中，在x=1200m处沿河流横向不同距离采集水样，实测得数据y(i)，ρ(i)。利用SCE-UA算法对Dy、ux进行识别，所形成的优化问题目标函数为

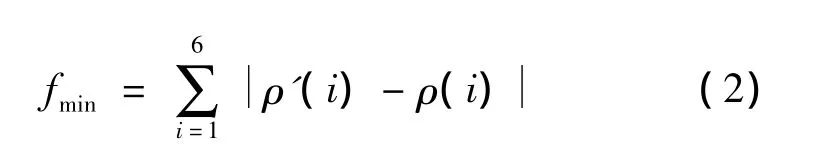
式中:fmin为目标函数值;ρ'(i)为根据解析式得到的在y(i)处的示踪剂浓度计算值。

对二维稳态水质模型横向扩散系数及流速的推求问题，由于在此优化问题中只有关于各决策变量的一元函数约束，故可以直接利用SCE-UA算法对优化模型进行求解，目标函数的优化过程见图1。迭代计算13次后，目标函数趋于稳定，此过程中目标函数被调了220次。优化结果为Dy=0.009 995 7，ux=1.0004，与真值Dy=0.01，ux=1.0非常接近，相对误差为0.04%。

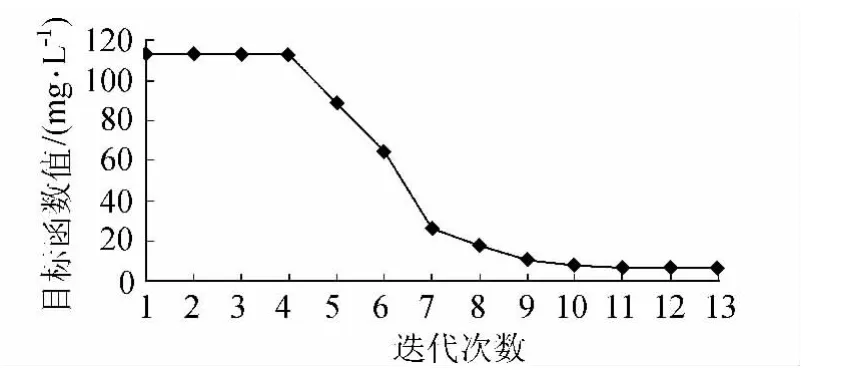
图1 目标函数的优化过程

2.2 排污口处理率最优化

排污口处理率最优化是指在一定的水质约束和技术约束条件下，寻求各污水厂最佳处理效率的组合。这个问题的基础是假设各污染源的污水处理规模不变，通过调整各处理厂的处理效率，使整个区域的污水处理费用最低。某河道［11］沿岸3个主要排污口污水处理效率的最优化模型为

式中:Fmin为最小处理总费用，元;ηi为第i个排放口的污水处理效率，i=1，2，3。

由于上述问题中含有多元函数约束，SCE-UA算法难以直接应用，为此需构造罚函数，把约束优化问题转化为无约束优化问题，构造的罚函数形式为

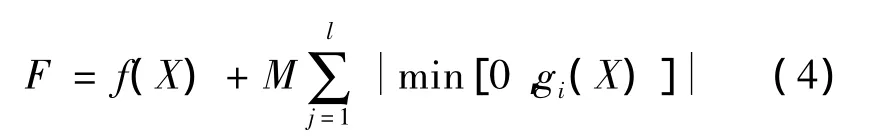
式中:X为目标变量;f(X)为原目标函数;M为惩罚因子，在求解之前要先化成标准形式;gi(X)为约束，i=1，2，…，l。

用二次规划算法求解上述排污口最优化处理问题，其真值为:η1=0.987，η2=0.421，η3=0.023，Fmin=1435.447。应用SCE-UA算法对排污口优化模型进行求解，构造罚函数，M取为100000，排污口处理率优化模型求解过程见图2，最优解为η1=0.98631，η2=0.42458，η3=0.022395，Fmin=1435.668，其中处理总费用的相对误差为0.02%，与真值非常接近，满足工程实际的需要。

2.3 生态优化调度

在很多水环境优化模型中，都存在目标函数不可导的问题，一般算法在求解时必须进行导数推求，而此类问题难以求导，因此难以解决此类优化问题。但SCE-UA算法在求解时不依赖任何导数信息，且在水文模型参数率定中取得较好效果，因此可以尝试将其与水动力模型结合，用于优化生态调度。

图2 排污口处理率优化模型求解过程

现以磨洋河水系生态调度优化为例进行说明。由于河道地形的原因，磨洋河水系流量自行分配不合理，需要新建水闸对流量进行控制，以得到合理的河段流量，建闸位置如图3所示。现以闸门的控制高度为决策变量，对调度进行优化，使得陈厝河分配流量为0.5m3/s，福兴河与新厝河分配流量为1m3/s，各河段的水流流向如图3所示。衡量每个目标点(水工建筑物)处流量调控效果的评价函数可用式(5)表示。由于是河网调控问题，存在多个目标点，为了把多目标优化转化为单一目标优化，可以对不同的评价函数加一个权重。最后得到的优化模型的目标函数见式(5)～(6):

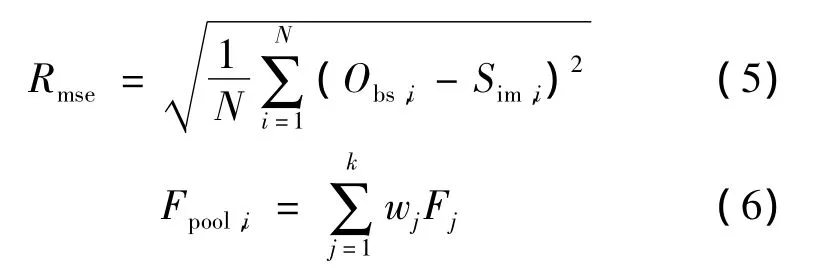
式中:Rmse为评价函数值;Obs，i、Sim，i分别为第i个目标值与模拟值(通过相应的河流动力学模型求解)时间序列，其中i=1，2，…，N;Fpool，i为目标函数值;k为评价函数的个数;wj为相应的评价函数的权重，j=1，2，…，k;Fj为第j个评价函数。此次优化中，各评价函数的权重取为1。

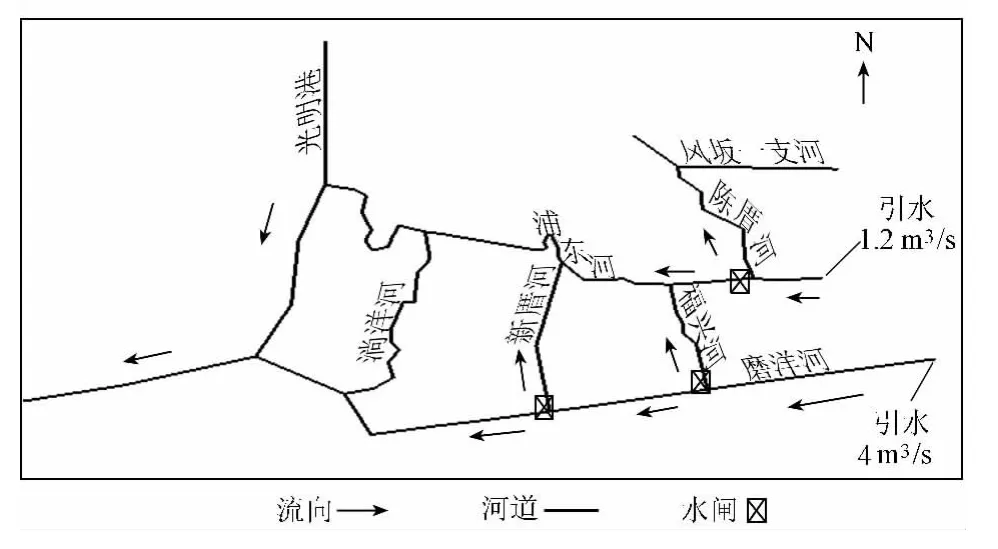
图3 磨洋河水系生态调度示意图

最后，可以概化出如下优化模型:式中:m为参数个数;θi为第i个参数，i=1，2，…，m;θmin，i和 θmax，i分别为m个参数的取值上、下限。

优化结果:应用SCE-UA算法对优化模型进行求解，目标函数仅被调用167次，便满足了算法终止准则，浦东河上水闸闸门高程为5.27m，福兴河上水闸闸门高程为4.92 m，新厝河上水闸闸门高程为4.66 m，调控后的河道分流流量如图4所示。

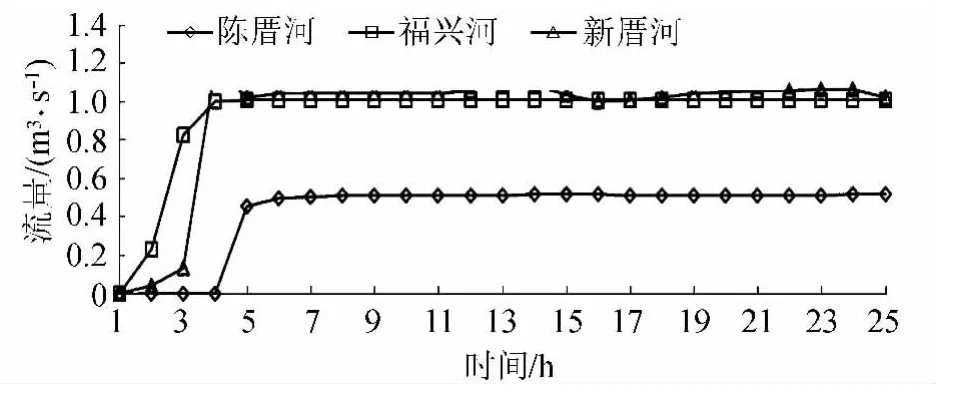
图4 磨洋河水系优化调度后河道分流效果

3 结语

SCE-UA算法的精度和效率很高，不但可以优化无约束优化问题，还可以处理经罚函数法处理后的有约束优化问题以及经权重法处理后的多目标优化问题，在水环境模型优化问题中能广泛应用;该算法不依赖导数与优化问题的具体形式，能够有效求解高度非线性优化问题。总之，SCE-UA算法所需参数较少，应用简单方便，适用性广，在水环境系统优化问题的求解中有很高的推广价值。

［1］郭建青，张勇.确定河流横向扩散系数的直线图解法［J］.水利学报，1997(1):62-67.(GUO Jianqing，ZHANG Yong.Linear graphics method for determining the transverse diffusion coefficient of river［J］.Journal of Hydraulic Engineering，1997(1):62-67.(in Chinese))

［2］杨晓华，张志峰，郦建强.蚁群加速遗传算法在水环境优化问题中的应用［J］.水电能源科学，2003，21(4):43-45.(YANG Xiaohua，ZHANG Zhifeng，LI Jianqiang.Apptication of ant colony accelerating genetic algorithm for parameter identification in water environment model［J］.International Journal Hydroelectric Energy，2003，21(4):43-45.(in Chinese))

［3］DUAN Q Y，GUPTA V K，SOROOSHIAN S.Shuffled complex evolution approach for effective and efficient global minimization［J］.Journal of Optimization Theory and Application，1993，76(3):501-521.

［4］ECKHARDT K，ARNOLD J G.Automatic calibration of a distributed catchment model［J］.Journal of Hydrology，2001，251(1/2):103-109.

［5］宋星原，苏全英，王海波，等.SCE-UA、遗传算法和单纯形优化算法的应用［J］.武汉大学学报:工学版，2009，42(1):6-9.(SONG Xingyuan，SU Quanying，WANG Haibo，et al.Comparison and application of SCE-UA，genetic algorithm and simplex method［J］.Engineering Journal of Wuhan University，2009，42(1):6-9.(in Chinese))

［6］雷晓辉，廖卫红，蒋云钟，等.分布式水文模型EasyDHM模型［J］.水利信息化，2010(2):31-37.(LEI Xiaohui，LIAO Weihong，JIANG Yunzhong，et al.A distributed hydrological model-easy DHM model［J］.Automation in Water Resources and Hydrology，2010(2):31-37.(in Chinese))

［7］辛朋磊，陈建标.基于全局优化的南通市水资源优化配置研究［J］.人民长江，2012，43(17):55-60.(XIN Penglei， CHEN Jianbiao， Optimal water resources allocation of Nantong City based on SCE-UA method［J］.Yangtze River，2012，43(17):55-60.(in Chinese))

［8］唐运忆，栾承梅.SCE-UA算法在新安江模型及TOPMODEL参数优化应用中的研究［J］.水文，2007，27(6):33-35.(TANGYunyi，LUAN Chengmei.Application of SCE-UA method in calibrating parameters of Xinanjiang Model and TOPMODEL［J］.Journal of China Hydrology，2007，27(6):33-35.(in Chinese))

［9］马海波，董 增 川，张 文 明，等.SCE-UA 算 法 在TOPMODEL参数优化中应用［J］.河海大学学报:自然科学版，2006，34(4):361-365.(MA Haibo，DONG Zengchuan，ZHANG Wenming，et al.Application of SCEUA algorithm to optimization of TOPMODEL parameters［J］.Journal of Hohai University:Natural Sciences，2006，34(4):361-365.(in Chinese))

［10］唐和生，李鹏飞，范存新.基于SCE算法的结构系统识别［J］.振动工程学报，2010，23(3):243-248.(TANG Hesheng，LI Pengfei，FAN Cunxin.Shuffled complex evolution algorithm for structural system identification［J］.Journal of Vibration Engineering，2010，23(3):243-248.(in Chinese))

［11］刘首文，冯尚友.遗传算法及其在水污染控制系统规划中的应用［J］.武汉水利电力大学学报，1996，29(4):95-99.(LIU Shouwen，FENG Shangyou.Genetic algorithm and its application in water pollution control system planning［J］.Engineering Journal of Wuhan University，1996，29(4):95-99.(in Chinese))

Application of SCE-UA algorithm to water environmental system optimization

ZHANG Jing，ZHANG Wenting，XING Baolong
(College of Hydrology and Water Resources，Hohai University，Nanjing 210098，China)

The SCE-UA algorithm was used to solve the optimization problems of the water environmental system.

Through preprocessing the problems，this algorithm solved three typical optimization problems，which included(1)

calculation of the transverse diffusion coefficient and flow velocity of the two-dimensional steady water quality model，(2)outfall optimization，and(3)optimal scheduling of hydraulic construction.The results show that，not only can the SCE-UA algorithm solve the optimization problem of unary function constraints，it can also successfully solve the optimization problem of multivariate function constraints by constructing a penalty function.The algorithm does not depend on the derivative and the specific forms of the problems;it needs few parameters，but has high precision and strong versatility，and thus it can be widely applied to the optimization of environmental systems.

SCE-UA algorithm;water environmental system optimization;longitudinal diffusion coefficient calculation;outfall optimization;sluice operation

X321

A

1004-6933(2014)03-0061-04

10.3969/j.issn.1004-6933.2014.03.012

张景(1987—)，男，硕士研究生，主要研究方向为水资源环境。E-mail:saintitaly@sina.com

(收稿日期:2014-02-13 编辑:徐 娟)